Bifurcations of the symmetric quasi-periodic motion and Lyapunov dimension of a vibro-impact system

Abstract

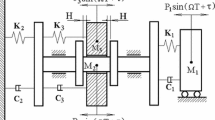
Under the suitable parameter combination, the vibro-impact system with symmetry exhibits symmetric quasi-periodic motions in the vicinity of Neimark–Sacker bifurcation (i.e., NS bifurcation) point satisfying 1:2 resonant conditions and double Neimark–Sacker bifurcation (i.e., NS–NS bifurcation) point. Based on the fact that the Poincaré map P is the second iteration of another virtual implicit map Q, the coexistence and symmetry of the attractor of the Poincaré map is discussed by means of the limit set theory. The map Q can capture two conjugate limit sets and hence can capture two conjugate quasi-periodic motions. Based on the Poincaré map, QR method is used to compute Lyapunov dimension, which can be used to characterize various quasi-periodic motions. Numerical simulation shows that the symmetric quasi-periodic motion can lose the stability and bifurcate into various subharmonic quasi-periodic motions via period-doubling bifurcation. Torus bifurcation of the symmetric quasi-periodic motion can also take place, which induces to a symmetric torus in the Poincaré section. Bifurcation of quasi-periodic motion will give birth to the coexistence of quasi-periodic motion. It is shown that all quasi-periodic attractors have at least a zero Lyapunov exponent, but various quasi-periodic attractors have different Lyapunov dimensions.

Appendices

Appendix 1: The phase angle and the integration constants

For the symmetric period n-2 motion of the vibro-impact system (i.e., the associated symmetric fixed point of the Poincaré map), the phase angle $\tau$ in Eq. (8) is solved according to Eq. (12):

$$\begin{aligned} \tau _0 =\left\{ {{\begin{array}{l} {2\tan ^{-1}\left( \frac{S_{mn} \pm \sqrt{S_{mn}^2 +C_{mn}^2 -h_{mn}^2 }}{C_{mn} -h_{mn} }\right) ,h_{mn} \ne C_{mn} ;} \\ {2\tan ^{-1}\left( -\frac{h_{mn} +C_{mn} }{2S_{mn} }\right) ,h_{mn} =C_{mn} ;} \\ \end{array} }} \right. \end{aligned}$$

(52)

Inserting $\tau =\tau _0$ into Eq. (12), $a_1$ can be solved. Subsequently, all integration constants in Eq. (8) can be solved as

$$\begin{aligned} a_1= & {} \frac{-m_c \cos \tau _0 -m_s \sin \tau _0 -m_h }{m_a },\end{aligned}$$

(53)

$$\begin{aligned} a_2= & {} \frac{\left| U \right| }{\left| G \right| }a_1 ,\end{aligned}$$

(54)

$$\begin{aligned} a_3= & {} p_{o4} a_1 +d_{o4} \cos \tau _0 +f_{o4} \sin \tau _0 +\frac{h}{o_4 },\end{aligned}$$

(55)

$$\begin{aligned} b_1= & {} \frac{\left| Q \right| }{\left| G \right| }a_1 ,\end{aligned}$$

(56)

$$\begin{aligned} b_2= & {} \frac{\left| V \right| }{\left| G \right| }a_1 ,\end{aligned}$$

(57)

$$\begin{aligned} b_3= & {} p_{og3} a_1 +d_{og3} \cos \tau _0 +f_{og3} \sin \tau _0 +h_3 , \end{aligned}$$

(58)

where

$$\begin{aligned} C_{mn}= & {} m_c n_a -n_c m_a , \quad S_{mn} =m_s n_a -n_s m_a , \nonumber \\ h_{mn}= & {} m_h n_a -n_h m_a ,\end{aligned}$$

(59)

$$\begin{aligned} m_a= & {} p_6 +q_6 q_g +u_6 u_g +v_6 v_g\nonumber \\&+o_6 p_{o4} +g_6 p_{og3} , \nonumber \\ m_c= & {} o_6 d_{o4} +g_6 d_{og3} +d_6 , \nonumber \\ m_s= & {} o_6 f_{o4} +g_6 d_{og3} +f_6 ,\nonumber \\ m_h= & {} \frac{o_6 h}{o_4 }+g_6 h_3 ,\end{aligned}$$

(60)

$$\begin{aligned} n_a= & {} p_7 +q_7 q_g +u_7 u_g +v_7 v_g \nonumber \\&+\,o_7 p_{o4} +g_7 p_{og3} ,\nonumber \\ n_c= & {} o_7 d_{o4} +g_7 d_{og3} +d_7 , \nonumber \\ n_s= & {} o_7 f_{o4} +g_7 d_{og3} +f_7 , \quad m_h =\frac{o_7 h}{o_4 }+g_7 h_3 ,\nonumber \\\end{aligned}$$

(61)

$$\begin{aligned} G= & {} \left[ {{ \begin{array}{ccc} {q_1 }&{} {u_1 }&{} {v_1 } \\ {q_2 }&{} {u_2 }&{} {v_2 } \\ {q_5 }&{} {u_5 }&{} {v_5 } \\ \end{array} }} \right] ,\nonumber \\ Q= & {} \left[ {{\begin{array}{ccc} {-p_1 }&{} {u_1 }&{} {v_1 } \\ {-p_2 }&{} {u_2 }&{} {v_2 } \\ {-p_5 }&{} {u_5 }&{} {v_5 } \\ \end{array} }} \right] , \quad U=\left[ {{\begin{array}{ccc} {q_1 }&{} {-p_1 }&{} {v_1 } \\ {q_2 }&{} {-p_2 }&{} {v_2 } \\ {q_5 }&{} {-p_5 }&{} {v_5 } \\ \end{array} }} \right] , \nonumber \\ V= & {} \left[ {{\begin{array}{ccc} {q_1 }&{} {u_1 }&{} {-p_1 } \\ {q_2 }&{} {u_2 }&{} {-p_2 } \\ {q_5 }&{} {u_5 }&{} {-p_5 } \\ \end{array} }} \right] ,\end{aligned}$$

(62)

$$\begin{aligned} p_{o4}= & {} -\frac{p_4 +u_4 u_g }{o_4 }, \quad d_{o4} =-\frac{d_4 }{o_4 }, \nonumber \\ f_{o4}= & {} -\frac{f_4 }{o_4 },\end{aligned}$$

(63)

$$\begin{aligned} p_{og3}= & {} -\frac{o_3 }{g_3 }p_{o4} , \quad d_{og3} =-\frac{o_3 }{g_3 }d_{o4} , \quad f_{og3} =-\frac{o_3 }{g_3 }f_{o4} ,\nonumber \\ h_3= & {} -\frac{o_3 }{o_4 g_3 }h, \end{aligned}$$

(64)

where

$$\begin{aligned} p_1= & {} \psi _{11} (1+e_1 \cos (\omega _{d1} t_1 )), \quad q_1 =\psi _{11} e_1 \sin (\omega _{d1} t_1 ),\nonumber \\ u_1= & {} \psi _{12} (1+e_2 \cos (\omega _{d2} t_1 )), \quad v_1 =\psi _{12} e_2 \sin (\omega _{d2} t_1 ),\nonumber \\\end{aligned}$$

(65)

$$\begin{aligned} p_2= & {} \psi _{21} (1+e_1 \cos (\omega _{d1} t_1 )), \quad q_2 =\psi _{21} e_1 \sin (\omega _{d1} t_1 ),\nonumber \\ u_2= & {} \psi _{22} (1+e_2 \cos (\omega _{d2} t_1 )), \quad v_2 =\psi _{22} e_2 \sin (\omega _{d2} t_1 ),\nonumber \\\end{aligned}$$

(66)

$$\begin{aligned} o_3= & {} 1+e_3 \cos (\omega _{d3} t_1 ), \quad g_3 =e_3 \sin (\omega _{d3} t_1 ),\end{aligned}$$

(67)

$$\begin{aligned} p_4= & {} \psi _{21} , u_4 =\psi _{22} ,\quad , f_4=\psi _{21} A_1 +\psi _{22} A_2 -A_3 , \nonumber \\ d_4= & {} \psi _{21} B_1 +\psi _{22} B_2 -B_3 , \end{aligned}$$

(68)

$$\begin{aligned} p_5= & {} \psi _{11} \eta _1 +\psi _{11} e_1 (\eta _1 \cos (\omega _{d1} t_1 )+\omega _{d1} \sin (\omega _{d1} t_1 )),\nonumber \\ q_5= & {} -\psi _{11} \omega _{d1} -\psi _{11} e_1 (\omega _{d1} \cos (\omega _{d1} t_1 )\nonumber \\&-\eta _1 \sin (\omega _{d1} t_1 )),\nonumber \\ u_5= & {} \psi _{12} \eta _2 +\psi _{12} e_2 (\eta _2 \cos (\omega _{d2} t_1 )+\omega _{d2} \sin (\omega _{d2} t_1 )),\nonumber \\ v_5= & {} -\psi _{12} \omega _{d2} -\psi _{12} \nonumber \\&\times \,e_2 (\omega _{d2} \cos (\omega _{d2} t_1 )-\eta _2 \sin (\omega _{d2} t_1 )), \end{aligned}$$

(69)

$$\begin{aligned} p_6= & {} \psi _{21} \eta _1 +m_1 \psi _{21} e_1 (\eta _1 \cos (\omega _{d1} t_1)\nonumber \\&+\omega _{d1} \sin (\omega _{d1} t_1 )),\nonumber \\ q_6= & {} -\psi _{21} \omega _{d1} -m_1 \psi _{21} e_1 (\omega _{d1} \cos (\omega _{d1} t_1)\nonumber \\&-\eta _1 \sin (\omega _{d1} t_1 )),\nonumber \\ u_6= & {} \psi _{22} \eta _2 +m_1 \psi _{22} e_2 (\eta _2 \cos (\omega _{d2} t_1)\nonumber \\&+\omega _{d2} \sin (\omega _{d2} t_1 )),\nonumber \\ v_6= & {} -\psi _{22} \omega _{d2} -m_1 \psi _{22} e_2 (\omega _{d2} \cos (\omega _{d2} t_1)\nonumber \\&-\eta _2 \sin (\omega _{d2} t_1 )),\nonumber \\ o_6= & {} n_1 e_3 (\eta _3 \cos (\omega _{d3} t_1 )+\omega _{d3} \sin (\omega _{d3} t_1 )),\nonumber \\ g_6= & {} -n_1 e_3 (\omega _{d3} \cos (\omega _{d3} t_1 )-\eta _3 \sin (\omega _{d3} t_1 )),\nonumber \\ d_6= & {} (-\psi _{21} A_1 -\psi _{22} A_2 +m_1 \psi _{21} A_1 \nonumber \\&+m_1 \psi _{22} A_2 +n_1 A_3 )\omega ,\nonumber \\ f_6= & {} (\psi _{21} B_1 +\psi _{22} B_2 -m_1 \psi _{21} B_1 \nonumber \\&-m_1 \psi _{22} B_2 -n_1 B_3 )\omega , \end{aligned}$$

(70)

$$\begin{aligned} p_7= & {} m_2 \psi _{21} e_1 (\eta _1 \cos (\omega _{d1} t_1 )+\omega _{d1} \sin (\omega _{d1} t_1 )),\nonumber \\ q_7= & {} -m_2 \psi _{21} e_1 (\omega _{d1} \cos (\omega _{d1} t_1 )-\eta _1 \sin (\omega _{d1} t_1 )),\nonumber \\ u_7= & {} m_2 \psi _{22} e_2 (\eta _2 \cos (\omega _{d2} t_1 )+\omega _{d2} \sin (\omega _{d2} t_1 )),\nonumber \\ v_7= & {} -m_2 \psi _{22} e_2 (\omega _{d2} \cos (\omega _{d2} t_1 )-\eta _2 \sin (\omega _{d2} t_1 )),\nonumber \\ o_7= & {} \eta _3 +n_2 e_3 (\eta _3 \cos (\omega _{d3} t_1 )+\omega _{d3} \sin (\omega _{d3} t_1 )),\nonumber \\ g_7= & {} -\omega _{d3} -n_2 e_3 (\omega _{d3} \cos (\omega _{d3} t_1 )-\eta _3 \sin (\omega _{d3} t_1 )),\nonumber \\ d_7= & {} (-A_3 +m_2 \psi _{21} A_1 +m_2 \psi _{22} A_2 +n_2 A_3 )\omega ,\nonumber \\ f_7= & {} (B_3 -m_2 \psi _{21} B_1 -m_2 \psi _{22} B_2 -n_2 B_3 )\omega , \end{aligned}$$

(71)

where

$$\begin{aligned} e_i =e^{-\eta _i t_1 }, \quad t_1 =\frac{n\pi }{\omega }. \end{aligned}$$

(72)

Appendix 2: The integration constants $a_{ij}$ and $b_{ij}$ determined by the initial conditions after impacting

Let the initial conditions be $x_{10}$, $\dot{x}_{10}$, $x_{20}$, $\dot{x}_{20}$, $\dot{x}_{30}$, $\tau _0$, the integration constants $a_{i1}$ and $b_{i1}$ after impacting at the right stop can be expressed as

$$\begin{aligned} \left. {{\begin{array}{rcl} a_{11} &{}=&{}U_{a1} \sin \tau _0 +V_{a1} \cos \tau _0 +P_{a1} x_{10} +Q_{a1} x_{20} , \\ a_{21} &{}=&{}U_{a2} \sin \tau _0 +V_{a2} \cos \tau _0 +P_{a2} x_{10} +Q_{a2} x_{20} , \\ a_{31} &{}=&{}U_{a3} \sin \tau _0 +V_{a3} \cos \tau _0 +P_{a3} x_{10} +Q_{a3} x_{20} -h, \\ b_{11} &{}=&{}U_{b1} \sin \tau _0 +V_{b1} \cos \tau _0 +P_{b1} x_{10} +Q_{b1} x_{20} +M_{b1} \dot{x}_{10} +N_{b1} \dot{x}_{20} , \\ b_{21} &{}=&{}U_{b2} \sin \tau _0 +V_{b2} \cos \tau _0 +P_{b2} x_{10} +Q_{b2} x_{20} +M_{b2} \dot{x}_{10} +N_{b2} \dot{x}_{20} , \\ b_{31} &{}=&{}U_{b3} \sin \tau _0 +V_{b3} \cos \tau _0 +P_{b3} x_{10} +Q_{b3} x_{20} +M_{b3} \dot{x}_{30} -\frac{\eta _3 h}{\omega _{d3} }, \\ \end{array} }} \right\} \end{aligned}$$

(73)

and the integration constants $a_{i2}$ and $b_{i2}$ after impacting at the left stop can be expressed as

$$\begin{aligned} \left. {{\begin{array}{rcl} a_{12} &{}=&{}U_{a1} \sin \tau _0^{\prime } +V_{a1} \cos \tau _0^{\prime } +P_{a1} x_{10}^{\prime } +Q_{a1} x_{20}^{\prime } , \\ a_{22} &{}=&{}U_{a2} \sin \tau _0^{\prime } +V_{a2} \cos \tau _0^{\prime } +P_{a2} x_{10}^{\prime } +Q_{a2} x_{20}^{\prime } , \\ a_{32} &{}=&{}U_{a3} \sin \tau _0^{\prime } +V_{a3} \cos \tau _0^{\prime } +P_{a3} x_{10}^{\prime } +Q_{a3} x_{20}^{\prime } +h, \\ b_{12} &{}=&{}U_{b1} \sin \tau _0^{\prime } +V_{b1} \cos \tau _0^{\prime } +P_{b1} x_{10}^{\prime } +Q_{b1} x_{20}^{\prime } +M_{b1} \dot{x}_{10}^{\prime } +N_{b1} \dot{x}_{20}^{\prime } , \\ b_{22} &{}=&{}U_{b2} \sin \tau _0^{\prime } +V_{b2} \cos \tau _0^{\prime } +P_{b2} x_{10}^{\prime } +Q_{b2} x_{20}^{\prime } +M_{b2} \dot{x}_{10}^{\prime } +N_{b2} \dot{x}_{20}^{\prime } , \\ b_{32} &{}=&{}U_{b3} \sin \tau _0^{\prime } +V_{b3} \cos \tau _0^{\prime } +P_{b3} x_{10}^{\prime } +Q_{b3} x_{20}^{\prime } +M_{b3} \dot{x}_{30}^{\prime } +\frac{\eta _3 h}{\omega _{d3} }, \\ \end{array} }} \right\} \end{aligned}$$

(74)

where

$$\begin{aligned}&(x_{10}^{\prime } ,{\dot{x}}'_{10} ,{x}'_{20} ,{\dot{x}}'_{20} ,\dot{x}_{30}^{\prime } ,{\tau }'_0 )= (-x_{10} ,-\dot{x}_{10} ,-x_{20} ,\nonumber \\&\quad -\dot{x}_{20} ,-\dot{x}_{30} ,\tau _0 +n\pi ),\end{aligned}$$

(75)

$$\begin{aligned}&U_{a1} =\frac{u_{sa1} }{\left| {D_a } \right| }, \quad V_{a1} =\frac{v_{ca1} }{\left| {D_a } \right| }, \quad P_{a1} =\frac{\psi _{22} }{\left| {D_a } \right| }, \nonumber \\&Q_{a1} =-\frac{\psi _{12} }{\left| {D_a } \right| },\end{aligned}$$

(76)

$$\begin{aligned}&U_{a2} =\frac{u_{sa2} }{\left| {D_a } \right| }, \quad V_{a2} =\frac{v_{ca2} }{\left| {D_a } \right| }, \quad P_{a2} =-\frac{\psi _{21} }{\left| {D_a } \right| }, \nonumber \\&Q_{a2} =\frac{\psi _{11} }{\left| {D_a } \right| },\end{aligned}$$

(77)

$$\begin{aligned}&U_{a3} =\psi _{21} U_{a1} +\psi _{21} A_1 +\psi _{22} A_2 -A_3 , \nonumber \\&V_{a3} =\psi _{21} V_{a1} +\psi _{21} B_1 +\psi _{22} B_2 -B_3,\nonumber \\&P_{a3} =\psi _{21} P_{a1} +\psi _{22} P_{a2} , \nonumber \\&Q_{a3} =\psi _{21} Q_{a1} +\psi _{22} Q_{a2} , \end{aligned}$$

(78)

$$\begin{aligned}&U_{b1} =\frac{u_{sb1} }{\left| {D_b } \right| }, \quad V_{b1} =\frac{v_{cb1} }{\left| {D_b } \right| }, \quad P_{b1} =\frac{p_{xb1} }{\left| {D_b } \right| }, \nonumber \\&Q_{b1} =-\frac{q_{xb1} }{\left| {D_b } \right| }, \quad M_{b1} =\frac{m_{xb1} }{\left| {D_b } \right| },\nonumber \\&N_{b1} =\frac{n_{xb1} }{\left| {D_b } \right| },\end{aligned}$$

(79)

$$\begin{aligned}&U_{b2} =\frac{u_{sb2} }{\left| {D_b } \right| }, \quad V_{b2} =\frac{v_{cb2} }{\left| {D_b } \right| }, \quad P_{b2} =\frac{p_{xb2} }{\left| {D_b } \right| }, \nonumber \\&Q_{b2} =-\frac{q_{xb2} }{\left| {D_b } \right| }, \quad M_{b2} =\frac{m_{xb2} }{\left| {D_b } \right| }, \quad N_{b2} =\frac{n_{xb2} }{\left| {D_b } \right| },\nonumber \\\end{aligned}$$

(80)

$$\begin{aligned}&U_{b3} =\frac{\eta _3 U_{a3} +B_3 \omega }{\omega _{d3} }, \quad V_{b3} =\frac{\eta _3 V_{a3} -A_3 \omega }{\omega _{d3} }, \nonumber \\&P_{b3} =\frac{\eta _3 P_{a3} }{\omega _{d3} }, Q_{b3}=\frac{\eta _3Q_{a3}}{\omega _{d3}} , \quad M_{b3} =\frac{1}{\omega _{d3} }, \end{aligned}$$

(81)

where

$$\begin{aligned} D_a= & {} \psi , \quad D_b =\left[ {{ \begin{array}{cc} {\psi _{11} \omega _{d1} }&{} {\psi _{12} \omega _{d2} } \\ {\psi _{21} \omega _{d1} }&{} {\psi _{22} \omega _{d2} } \\ \end{array} }} \right] , \end{aligned}$$

(82)

$$\begin{aligned} u_{sa1}= & {} \psi _{12} (\psi _{21} A_1 +\psi _{22} A_2 )\nonumber \\&-\psi _{22}(\psi _{11} A_1 +\psi _{12} A_2 ),\nonumber \\ v_{ca1}= & {} \psi _{12} (\psi _{21} B_1 +\psi _{22} B_2 )\nonumber \\&-\psi _{22}(\psi _{11} B_1 +\psi _{12} B_2 ),\end{aligned}$$

(83)

$$\begin{aligned} u_{sa2}= & {} \psi _{22} (\psi _{11} A_1 +\psi _{12} A_2 )\nonumber \\&-\psi _{11} (\psi _{21} A_1 +\psi _{22} A_2 ),\nonumber \\ v_{ca2}= & {} \psi _{21} (\psi _{11} B_1 +\psi _{12} B_2 )\nonumber \\&-\psi _{11} (\psi _{21} B_1 +\psi _{22} B_2 ),\end{aligned}$$

(84)

$$\begin{aligned} u_{sb1}= & {} \psi _{22} \omega _{d2} u_{s1} -\psi _{12} \omega _{d2} u_{s2} ,\nonumber \\ v_{cb1}= & {} \psi _{22} \omega _{d2} v_{s1} -\psi _{12} \omega _{d2} v_{s2} ,\nonumber \\ p_{xb1}= & {} \psi _{22} \omega _{d2} p_{s1} -\psi _{12} \omega _{d2} p_{s2} ,\nonumber \\ q_{xb1}= & {} \psi _{22} \omega _{d2} q_{s1} -\psi _{12} \omega _{d2} q_{s2} ,\nonumber \\ m_{xb1}= & {} \psi _{22} \omega _{d2} , n_{xb1} =-\psi _{12} \omega _{d2},\end{aligned}$$

(85)

$$\begin{aligned} u_{sb2}= & {} \psi _{11} \omega _{d1} u_{s2} -\psi _{21} \omega _{d1} u_{s1} ,\nonumber \\ v_{cb2}= & {} \psi _{11} \omega _{d1} v_{s2} -\psi _{21} \omega _{d1} v_{s1} ,\nonumber \\ p_{xb2}= & {} \psi _{11} \omega _{d1} p_{s2} -\psi _{21} \omega _{d1} p_{s1} ,\nonumber \\ q_{xb2}= & {} \psi _{11} \omega _{d1} q_{s2} -\psi _{21} \omega _{d1} q_{s1} ,\nonumber \\ m_{xb2}= & {} -\psi _{21} \omega _{d1} , n_{xb2} =\psi _{11} \omega _{d1} , \end{aligned}$$

(86)

where

$$\begin{aligned} u_{s1}= & {} \psi _{11} \eta _1 U_{a1} +\psi _{12} \eta _2 U_{a2} +\psi _{11} B_1 \omega +\psi _{12} B_2 \omega ,\nonumber \\ v_{s1}= & {} \psi _{11} \eta _1 V_{a1} +\psi _{12} \eta _2 V_{a2} -\psi _{11} A_1 \omega -\psi _{12} A_2 \omega ,\nonumber \\ p_{s1}= & {} \psi _{11} \eta _1 P_{a1} +\psi _{12} \eta _2 P_{a2} , \quad q_{s1} =\psi _{11} \eta _1 q_{a1} \nonumber \\&+\psi _{12} \eta _2 q_{a2} , \end{aligned}$$

(87)

$$\begin{aligned} u_{s2}= & {} \psi _{21} \eta _1 U_{a1} +\psi _{22} \eta _2 U_{a2} +\psi _{21} B_1 \omega +\psi _{22} B_2 \omega ,\nonumber \\ v_{s2}= & {} \psi _{21} \eta _1 V_{a1} +\psi _{22} \eta _2 V_{a2} -\psi _{21} A_1 \omega -\psi _{22} A_2 \omega ,\nonumber \\ p_{s2}= & {} \psi _{21} \eta _1 P_{a1} +\psi _{22} \eta _2 P_{a2} , \nonumber \\ q_{s2}= & {} \psi _{21} \eta _1 q_{a1} +\psi _{22} \eta _2 q_{a2} . \end{aligned}$$

(88)