Nonlinear harmonic vibration and stability analysis of a cantilever beam carrying an intermediate lumped mass

Abstract

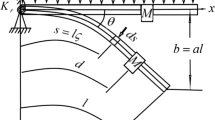
Nonlinear forced vibration of a cantilever beam with an intermediate lumped mass is studied, and the nonlinear governing equation of the vibrating beam using Euler–Lagrange method is derived. Two types of nonlinearities, including the inertial term and the elastic part, are included in the nonlinear differential equation of motion. The multiple scales method is adopted as the solution procedure for this problem and the conditions of the primary and secondary resonances of the system are investigated. The frequency response diagrams of the cantilever beam for the fundamental harmonic vibration, super-harmonic condition $({\omega }\approx \frac{1}{2}{\omega }_0,\,{\omega }\approx \frac{1}{3}{\omega }_0\hbox { and }{\omega }\approx \frac{1}{5}{\omega }_0 )$ and also sub-harmonic condition $({\omega }\approx 2\omega _0,\,{\omega }\approx 3\omega _0\hbox { and }{\omega }\approx 5\omega _0 )$ are obtained. The stable and unstable segments of each frequency-response curves are then numerically determined. It is shown that the frequency response of the cantilever beam is strongly affected by damping and excitation level. Particularly, for the sub-harmonic resonance of the system, instability can be observed by increasing the amplitude of excitation. As for a detailed parameter sensitivity study, the influences of different parameters on the frequency response of the cantilever beam have been examined. By varying the values of the parameters of the model, it is found that transition from the periodic solution to chaos occurred for the mechanical system.

Appendix

$H\left( {A,{{\varLambda }},{\varOmega },T_0 } \right)$ in Eq. (26) is defined as:

$$\begin{aligned}&H\left( {A,{{\varLambda }},{\varOmega },T_{0} } \right) = \left( - 6A{\varLambda }^{2} \alpha _{1} - 3A^{2} \bar{A}\alpha _{1} - 30A{\varLambda }^{4} \alpha _{2} \right. \\&\quad -\,60A^{2} {\varLambda }^{2} \bar{A}\alpha _{2} - 10A^{3} \bar{A}^{2} \alpha _{2}\\&\quad +\, 2A{\varLambda }^{2} {\varOmega }^{2} \beta _{1} + 18A{\varLambda }^{4} {\varOmega }^{2} \beta _{2} + 18A^{2} {\varLambda }^{2} {\varOmega }^{2} \bar{A}\beta _{2} \\&\quad -\,{i}A\mu + 2A{\varLambda }^{2} \beta _{1} + 2A^{2} \bar{A}\beta _{1}\\&\quad +\left. \, 6A{\varLambda }^{4} \beta _{2} + 30A^{2} {\varLambda }^{2} \bar{A}\beta _{2} + 8A^{3} \bar{A}^{2} \beta _{2} - 2{i}A^{\prime }\right) {e}^{{{{i}}T_{0} }} ~ \\&\quad +\, \left( - {{i}}{\varLambda }\mu {\varOmega }- 3{\varLambda }^{3} \alpha _{1}\right. \\&\quad -\, 6A{\varLambda }\bar{A}\alpha _{1} - 10{\varLambda }^{5} \alpha _{2} - 60A{\varLambda }^{3} \bar{A}\alpha _{2} \\&\quad -\, 30A^{2} {\varLambda }\bar{A}^{2} \alpha _{2} + 2{\varLambda }^{3} {\varOmega }^{2} \beta _{1}\\&\quad +\, 2A{\varLambda }{\varOmega }^{2} \bar{A}\beta _{1} + 8{\varLambda }^{5} {\varOmega }^{2} \beta _{2} + 30A{\varLambda }^{3} {\varOmega }^{2} \bar{A}\beta _{2} \\&\quad +\, 6A^{2} {\varLambda }{\varOmega }^{2} \bar{A}^{2} \beta _{2} + 2A{\varLambda }\bar{A}\beta _{1}\\&\quad \left. +\,18A{\varLambda }^{3} \bar{A}\beta _{2} + 18A^{2} {\varLambda }\bar{A}^{2} \beta _{2} \right) {{e}}^{{{{i}}{\varOmega }T_{0} }} \\&\quad +\, \left( { - A^{3} \alpha _{1} - 20A^{3} {\varLambda }^{2} \alpha _{2} - 5A^{4} \bar{A}\alpha _{2} } \right. \\&\quad +\, 6A^{3} {\varLambda }^{2} {\varOmega }^{2} \beta _{2} + 2A^{3} \beta _{1} + 18A^{3} {\varLambda }^{2} \beta _{2} \\&\quad \left. +\, 6A^{4} \bar{A}\beta _{2} \right) {{e}}^{{3{{i}}T_{0} }} + \left( - A^{5} \alpha _{2}\right. \\&\quad \left. +\, 2A^{5} \beta _{2} \right) {{e}}^{{5{{i}}T_{0} }} + \left( - {\varLambda }^{3} \alpha _{1} - 5{\varLambda }^{5} \alpha _{2} \right. \\&\quad \left. -\, 20A{\varLambda }^{3} \bar{A}\alpha _{2} + 2{\varLambda }^{3} {\varOmega }^{2} \beta _{1} + 6{\varLambda }^{5} {\varOmega }^{2} \beta _{2} \right. \\ \end{aligned}$$

$$\begin{aligned}&\quad \left. { +\, 18A{\varLambda }^{3} {\varOmega }^{2} \bar{A}\beta _{2} + 6A{\varLambda }^{3} \bar{A}\beta _{2} } \right) {{e}}^{{3{{i}}{\varOmega }T_{0} }} \\&\quad +\, \left( { - {\varLambda }^{5} \alpha _{2} + 2{\varLambda }^{5} {\varOmega }^{2} \beta _{2} } \right) {{e}}^{{5{{i}}{\varOmega }T_{0} }}\\&\quad +\, \left( - 3{\varLambda }\bar{A}^{2} \alpha _{1} - 30{\varLambda }^{3} \bar{A}^{2} \alpha _{2} - 20A{\varLambda }\bar{A}^{3} \alpha _{2} \right. \\&\quad +\, {\varLambda }{\varOmega }^{2} \bar{A}^{2} \beta _{1} + 15{\varLambda }^{3} {\varOmega }^{2} \bar{A}^{2} \beta _{2}\\&\quad +\, 4A{\varLambda }{\varOmega }^{2} \bar{A}^{3} \beta _{2} - 2{\varLambda }{\varOmega }\bar{A}^{2} \beta _{1} - 6{\varLambda }^{3} {\varOmega }\bar{A}^{2} \beta _{2} \\&\quad -\, 4A{\varLambda }{\varOmega }\bar{A}^{3} \beta _{2} + 3{\varLambda }\bar{A}^{2} \beta _{1}\\&\quad \left. +\, 15{\varLambda }^{3} \bar{A}^{2} \beta _{2} + 16A{\varLambda }\bar{A}^{3} \beta _{2} \right) e^{{{{i}}\left( {{\varOmega }- 2} \right) T_{0} }}\\&\quad +\, \left( - 3A^{2} {\varLambda }\alpha _{1} - 30A^{2} {\varLambda }^{3} \alpha _{2} - 20A^{3} {\varLambda }\bar{A}\alpha _{2} \right. \\&\quad \left. +\, A^{2} {\varLambda }{\varOmega }^{2} \beta _{1} + 15A \right. ^{2} {\varLambda }^{3} {\varOmega }^{2} \beta _{2}\\&\quad +\, 4A^{3} {\varLambda }{\varOmega }^{2} \bar{A}\beta _{2} + 2A^{2} {\varLambda }{\varOmega }\beta _{1} + 6A^{2} {\varLambda }^{3} {\varOmega }\beta _{2} \\&\quad +\, 4A^{3} {\varLambda }{\varOmega }\bar{A}\beta _{2} + 3A^{2} {\varLambda }\beta _{1}\\&\quad \left. { +\, 15A^{2} {\varLambda }^{3} \beta _{2} + 16A^{3} {\varLambda }\bar{A}\beta _{2} } \right) {{e}}^{{{{i}}\left( {{\varOmega }+ 2} \right) T_{0} }}\\&\quad +\, \left( - 5{\varLambda }\bar{A}^{4} \alpha _{2} + {\varLambda }{\varOmega }^{2} \bar{A}^{4} \beta _{2} \right. \\&\quad \left. -\, 2{\varLambda }{\varOmega }\bar{A}^{4} \beta _{2} + 7{\varLambda }\bar{A}^{4} \beta _{2} \right) e^{{{{i}}\left( {{\varOmega }- 4} \right) T_{0} }} + \left( - 5A^{4} {\varLambda }\alpha _{2}\right. \\&\quad +\, A^{4} {\varLambda }{\varOmega }^{2} \beta _{2} + 2A^{4} {\varLambda }{\varOmega }\beta _{2}\\&\quad \left. +\, 7A^{4} {\varLambda }\beta _{2} \right) {{e}}^{{{{i}}\left( {{\varOmega }+ 4} \right) T_{0} }} + \left( - 3{\varLambda }^{2} \bar{A}\alpha _{1} - 20{\varLambda }^{4} \bar{A}\alpha _{2} \right. \\&\quad -\, 30A{\varLambda }^{2} \bar{A}^{2} \alpha _{2} + 3{\varLambda }^{2} {\varOmega }^{2} \bar{A}\beta _{1}\\ \end{aligned}$$

$$\begin{aligned}&\quad +\, 16{\varLambda }^{4} {\varOmega }^{2} \bar{A}\beta _{2} + 15A{\varLambda }^{2} {\varOmega }^{2} \bar{A}^{2} \beta _{2} - 2{\varLambda }^{2} {\varOmega }\bar{A}\beta _{1} \nonumber \\&\quad -\, 4{\varLambda }^{4} {\varOmega }\bar{A}\beta _{2} - 6A{\varLambda }^{2} {\varOmega }\bar{A}^{2} \beta _{2}\nonumber \\&\quad \left. +\, {\varLambda }^{2} \bar{A}\beta _{1} + 4{\varLambda }^{4} \bar{A}\beta _{2} + 15A{\varLambda }^{2} \bar{A}^{2} \beta _{2} \right) e^{{{{i}}\left( {2{\varOmega }- 1} \right) T_{0} }} \nonumber \\&\quad +\, \left( - 3A{\varLambda }^{2} \alpha _{1} - 20A{\varLambda }^{4} \alpha _{2}\right. \nonumber \\&\quad -\, 30A^{2} {\varLambda }^{2} \bar{A}\alpha _{2} + 3A{\varLambda }^{2} {\varOmega }^{2} \beta _{1} + 16A{\varLambda }^{4} {\varOmega }^{2} \beta _{2} \nonumber \\&\quad +\, 15A^{2} {\varLambda }^{2} {\varOmega }^{2} \bar{A}\beta _{2} + 2A{\varLambda }^{2} {\varOmega }\beta _{1}\nonumber \\&\quad +\, 4A{\varLambda }^{4} {\varOmega }\beta _{2} + 6A^{2} {\varLambda }^{2} {\varOmega }\bar{A}\beta _{2} + A{\varLambda }^{2} \beta _{1} + 4A{\varLambda }^{4} \beta _{2}\nonumber \\&\quad \left. +\, 15A^{2} {\varLambda }^{2} \bar{A}\beta _{2} \right) {{e}}^{{{{i}}\left( {2{\varOmega }+ 1} \right) T_{0} }} \nonumber \\&\quad +\, \left( { - 10{\varLambda }^{2} \bar{A}^{3} \alpha _{2} + 5{\varLambda }^{2} {\varOmega }^{2} \bar{A}^{3} \beta _{2} - 6{\varLambda }^{2} {\varOmega }\bar{A}^{3} } \right. \beta _{2}\nonumber \\&\quad +\, \left. {9{\varLambda }^{2} \bar{A}^{3} \beta _{2} } \right) {{e}}^{{{{i}}\left( {2{\varOmega }- 3} \right) T_{0} }}\nonumber \\&\quad +\, \left( - 10A^{3} {\varLambda }^{2} \alpha _{2} + 5A^{3} {\varLambda }^{2} {\varOmega }^{2} \beta _{2} + 6A^{3} {\varLambda }^{2} {\varOmega }\beta _{2} \right. \nonumber \\&\quad \left. +\, 9A^{3} {\varLambda }^{2} \beta _{2} \right) {{e}}^{{{{i}}\left( {2{\varOmega }+ 3} \right) T_{0} }}\nonumber \\&\quad +\, \left( - 10{\varLambda }^{3} \bar{A}^{2} \alpha _{2} + 9{\varLambda }^{3} {\varOmega }^{2} \bar{A}^{2} \beta _{2} - 6{\varLambda }^{3} {\varOmega }\bar{A}^{2} \beta _{2}\right. \nonumber \\&\quad \left. +\, 5{\varLambda }^{3} \bar{A}^{2} \beta _{2}\right) {{e}}^{{{{i}}\left( {3{\varOmega }- 2} \right) T_{0} }} \nonumber \\&\quad +\, \left( { - 10A^{2} {\varLambda }^{3} \alpha _{2} + 9A^{2} {\varLambda }^{3} {\varOmega }^{2} \beta _{2} + 6A^{2} {\varLambda }^{3} {\varOmega }\beta _{2} } \right. \nonumber \\&\quad +\, \left. {5A^{2} {\varLambda }^{3} \beta _{2} } \right) {{e}}^{{{{i}}\left( {3{\varOmega }+ 2} \right) T_{0} }} \nonumber \\&\quad +\, \left( { - 5{\varLambda }^{4} \bar{A}\alpha _{2} + 7{\varLambda }^{4} {\varOmega }^{2} \bar{A}\beta _{2} - 2} \right. {\varLambda }^{4} {\varOmega }\bar{A}\beta _{2}\nonumber \\&\quad \left. +\, {\varLambda }^{4} \bar{A}\beta _{2} \right) {{e}}^{{{{i}}\left( {4{\varOmega }- 1} \right) T_{0} }} \nonumber \\&\quad +\, \left( - 5A{\varLambda }^{4} \alpha _{2} + 7A{\varLambda }^{4} {\varOmega }^{2} \beta _{2} + 2A{\varLambda }^{4} {\varOmega }\beta _{2}\right. \nonumber \\&\quad \left. +\, A{\varLambda }^{4} \beta _{2} \right) {{e}}^{{{{i}}\left( {4{\varOmega }+ 1} \right) T_{0} }} + \mathrm{c.c} \end{aligned}$$

(51)