1 Introduction

Rotational molding technology originated in the 1940s in the UK. Then, the technology was widely used in the USA and Japan and became one competitive method in the field of plastic forming [1–3] (Fig. 1).

A rotary-molded boat is often made of polyethylene material, which makes the boat not only pollution free, erosion resistant and alkali resistant, but also with large buoyancy, high speed and low repair cost. However, the existing boat construction methods are still based on steel-material ships. Though the rotary-molded boat is made of high-strength plastic, its rigidity will decrease when the load is too much or it rolls severely, and its deformation should not be neglected; thus, its stability will decrease too. Therefore, there is a hidden danger in stability evaluation in that the theoretical foundation for steel-material ships is not suitable to rotary-molded boats.

To the best of our knowledge, no literature on rotary-molded boat stability has been published. In this paper, we choose a rotary-molded fishing entertainment boat as the research object. We consider the elastic deformation of boat in the new roll motion equation and study the establishment of nonlinear roll motion equation and stability simulation.

Rolling is the most common ship motion. Rolling is also a crucial reason of overturning accidents [4–7]. In the nineteenth century, Krylov and Froude put forward early classical movement theories on ship longitudinal and transverse motion, respectively. There are voluminous literatures on ship stability. The theoretical basis of early studies was linear; i.e., many nonlinear factors were not considered. Therefore, the reasonable explanation for some phenomena such as sudden overturning cannot be given [8, 9]. With the gradual maturation of nonlinear dynamics theory, many scholars have made useful exploration on ship rolling. For instance, Li [10, 11] used the multiple scale method to establish ship nonlinear rolling equation in the case of regular waves. He found the approximate analytic solution of the nonlinear equation and succeeded in verifying the solution. Without considering the deformation and coupling, the nonlinear single-freedom-degree rolling equation can be expressed as

$$\begin{aligned}&(I_{x}+\delta I_{x}){\ddot{\varphi }}+D_{1}{\dot{\varphi }}+D_{3}{\dot{\varphi }}^{3}\nonumber \\&\qquad +\varDelta (\overline{{ GM }}\varphi +C_{3}\varphi ^{3}+C_{5}\varphi ^{5}+\cdots )\nonumber \\&\quad =M_{L}+M_{F} \end{aligned}$$
(1)
Fig. 1
figure 1

Contour diagram of a rotary-molded boat

Full size image

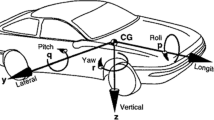
where \(I_x\) is the coherent rotation moment of inertia, \(\delta I_x\) is the additional rotation moment of inertia, \(\varphi \) is the roll angle which is positive in clockwise direction and negative in counterclockwise direction if looked from stern to bow, \(D_1\) and \(D_3\) are damping coefficients, \(\varDelta \) is displacement, \(\overline{{ GM }}\) is initial stability height, \(C_3\) and \(C_5\) are recovery coefficients, \(M_L\) is wave disturbance torque, \(M_F\) is wind disturbance torque. Assume that a two-dimensional irregular long crest wave propagates along a fixed direction, and it is superposed by many regular waves with different frequencies, wavelengths, amplitudes and random phases. Also assume that the crest lines are infinitely long and parallel to each other. Wave characteristic parameters such as wave height and wave period change randomly. Its mathematical expression is as follows:

$$\begin{aligned} \zeta (t)=\sum _{i=1}^\infty {\zeta _{i}\cos (\omega _{i}t+\varepsilon _{i})} \end{aligned}$$
(2)

where \(\zeta \) is the height of wave and \(\zeta _{i}\) is the amplitude of the ith harmonic wave.

In Eq. (1), the \(M_L\) can be expressed as

$$\begin{aligned} M_L =I\alpha _0 \omega _0^2 \pi \sum _{i=1}^\infty {\frac{h_i}{\lambda _i }\cos (\omega _i t+\varepsilon _i)} \end{aligned}$$
(3)

where I is the total inertia moment which includes the coherent rotation moment of inertia \(I_x\) and the additional rotation moment of inertia \(\delta I_x\), \(\alpha _0\) is the effective coefficient of wave inclination, \(\omega _0\) is the boat natural frequency, \(h_i\) is the significant wave height, \(\lambda _i\) is the wave wavelength, \(\omega _i\) is the wave frequency, and \(\varepsilon _i\) is the random phase angle which ranges from 0 to \(2\pi \) [12, 13].

Assume that the unsteady wind is composed of the mean part and the fluctuating part. The wind speed is

$$\begin{aligned} u_F =u_0 +\sum _{i=1}^\infty {u_i } \cos (\varOmega _i t+\theta _i ) \end{aligned}$$
(4)

where \(u_0\) is the average speed, \(u_i\) is the fluctuating amplitude, \(\varOmega _{i}\) is the pulsing frequency, and \(\theta _i\) is the fluctuating random phase. Wind force on the boat can be written as

$$\begin{aligned} f=\frac{1}{2}\rho _\mathrm{air} \cdot u_F^2 \cdot S \end{aligned}$$
(5)

where \(\rho _\mathrm{air}\) is air density and S is the upright-projection area of a boat hull above the waterline. Then, the wind disturbance torque \(M_F\) on the boat is written as

$$\begin{aligned} M_F= & {} f\cdot (H+d-z_R ) \nonumber \\= & {} \rho _\mathrm{air}\cdot u_F^2 \cdot S\cdot (H+d-z_R )/2 \end{aligned}$$
(6)

where H is the distance between wind pressure center and the water surface, d is the boat draft depth, and \(z_R\) is the distance between the water resistance action center and the baseline, which is approximately equal to d / 2. Therefore, when not considering the boat deformation, we can get a single-freedom-degree rolling equation of a rotary-molded boat as follows

$$\begin{aligned}&(I_x +\delta I_x )\ddot{\varphi }+D_1 \dot{\varphi }+D_3\dot{\varphi }^{3} \nonumber \\&\qquad +\varDelta (\overline{{ GM }} \varphi +C_3 \varphi ^{3}+C_5 \varphi ^{5}+\cdots )\nonumber \\&\quad =I\cdot \alpha _0 \cdot \omega _0^2 \cdot \pi \cdot \sum _{i=1}^\infty {\frac{h_i }{\lambda _i }\cos (\omega _i t+\varepsilon _i )}\nonumber \\&\quad \quad +\frac{1}{2}\rho _\mathrm{air} \cdot u_F^2 \cdot S\cdot (H+d-z_R ) \end{aligned}$$
(7)

2 A new rolling model of the rotary-molded boat

Because the material of a rotary-molded boat is polyethylene which has a small specific gravity value of about 900–960 \(\hbox {kg}/\hbox {m}^{3}\), it is necessary to consider deformation in establishing a more realistic rolling equation.

Assume the boat speed is zero and the heeling is only caused by wind and wave. We draw boat rolling state diagram without considering deformation as shown in Fig. 2, where point \(G_{0}\) is the center of gravity, \(B_{0}\) is the upright buoyancy center, \(B_{1}\) is the tilt buoyancy center, segment \(\overline{B_1S_1}\) is the reply lever, \(\overline{W_0L_0}\) is the upright waterline, and \(\overline{W_1L_1}\) is the inclined waterline. Let \(V_{1}\) and \(V_{2}\) be the water wedge volume induced by boat hull’s tilt. Let \(V_{0}\) be the floating displacement [14–18]. So the volume below the waterline after being tilted is

$$\begin{aligned} V=V_0+V_1-V_2 \end{aligned}$$
(8)

Assume that the boat hull’s deformation is only caused by crosswind. The wind pressure evenly distributes along the high free-board. Assume that deformation amount is x as shown in Fig. 3. When deformation happens, the gravity center, buoyancy center and displacement volume all change correspondingly. The gravity center changes from \(G_{0}\) to \(G_{1}\). The buoyancy center moves from \(B_{1}\) to \(B_{2}\). \(\overline{B_2S_2}\) is the new reversion arm. The position of the new gravity center \(G_{1}\) can be calculated based on the gravity center moving principal. For simplicity, assume that damping torque and response arm are constant. Assume \(\overline{B_1S_1}\approx \overline{B_2S_2}\). Then, the volume under water \(V'=V_0+(V_1+\delta V_1)-(V_2-\delta V_2)\), where \(\delta V_1\) is the volume of trapezoidal block and \(\delta V_2\) is the volume of trapezoidal block as shown in Fig. 3.

Fig. 2
figure 2

Rolling diagram without elastic deformation

Full size image
Fig. 3
figure 3

Rolling diagram with elastic deformation

Full size image

Here, \(\overline{56}=\tan \varphi \cdot a\), \(\overline{78} =\tan \varphi \cdot (a+x)\) and \(\overline{12} =\tan \varphi \cdot (B-a-x)\), \(\overline{34} =\tan \varphi \cdot (B-a)\).

$$\begin{aligned} \delta V_1= & {} \left( \frac{1}{2}(a+x)^{2}\cdot \tan \varphi -\frac{1}{2}a^{2}\cdot \tan \varphi \right) \cdot L \end{aligned}$$
(9)
$$\begin{aligned} \delta V_2= & {} \left( \frac{1}{2}(B-a)^{2}\cdot \tan \varphi -\frac{1}{2}(B-a-x)^{2}\cdot \tan \varphi \right) \cdot L\nonumber \\ \end{aligned}$$
(10)

Therefore, the change of drainage volume is,

$$\begin{aligned} \delta V={V}'-V=\delta V_1+\delta V_2=L\cdot B\cdot x\cdot \tan \varphi \end{aligned}$$
(11)

and the change of displacement is as below,

$$\begin{aligned} \delta \varDelta= & {} \delta V\cdot \rho _\mathrm{water} =L\cdot B\cdot x\cdot \tan \varphi \cdot \rho _\mathrm{water} \nonumber \\= & {} k_1\cdot x\cdot \tan \varphi \end{aligned}$$
(12)

Next, we describe the change of displacement as a function of wind speed. Because the deformation is assumed to be elastic, let \(f=k_2\cdot x\). Because \(f=\frac{1}{2}\rho _\mathrm{air} \cdot u_\mathrm{wind}^2 \cdot S\), so,

$$\begin{aligned} x=\frac{1}{2}\rho _\mathrm{air} \cdot u_\mathrm{wind}^2 \cdot S/k_2=k_3\cdot u_\mathrm{wind}^2 \end{aligned}$$
(13)

That is to say, the change of displacement is

$$\begin{aligned} \delta \varDelta= & {} k_1\cdot x\cdot \tan \varphi \nonumber \\= & {} k_1 \cdot k_3 \cdot u_F^2 \cdot \tan \varphi =K_1\cdot u_F^2 \cdot \tan \varphi \end{aligned}$$
(14)

where \(K_1\), \(k_1\), \(k_2\), \(k_3\), \(k_4\) are constant numbers to a specific boat. Thus, when elastic deformation is generated only by wind, the boat rolling motion equation is written as

$$\begin{aligned}&(I_{x}+\delta I_{x})\cdot {\ddot{\varphi }}+D_1 \cdot {\dot{\varphi }}+D_3 \cdot {\dot{\varphi }}^{3}\nonumber \\&\qquad +(\varDelta +K_{1}\cdot u_F^2 \cdot \tan \varphi )\nonumber \\&\qquad \cdot (\overline{{ GM }}\cdot \varphi +C_3\cdot \varphi ^{3}+C_5\cdot \varphi ^{5}+\cdot \cdot \cdot )\nonumber \\&\quad =I\cdot \alpha _0 \cdot \omega _0^2 \cdot \pi \cdot \sum _{i=1}^\infty {\frac{h_i}{\lambda _i}\cos (\omega _i t+\varepsilon _i)}\nonumber \\&\qquad +\,\frac{1}{2}\rho _\mathrm{air}\cdot u_\mathrm{wind}^2 \cdot S\cdot (H+d-z_R) \end{aligned}$$
(15)

Further study show that, the hydrodynamic impact which the wave acts on the boat should not be neglected, this impact will cause the boat’s bending and torsion deformation [19, 20]. Here, assuming that the wave direction is in line with the direction of the wind and is vertical to the central lateral plane of boat.

According to the water elastic mechanics theory, the impact force that the wave acts on the boat is [21, 22]:

$$\begin{aligned} F=\varDelta \cdot \overline{{ GM }} \cdot \sum _{i=1}^\infty {\pi \frac{hi}{\lambda _{i}}\cos (\omega _{i}t+\varepsilon _{i})} \end{aligned}$$
(16)

The deformation which is caused by the hydrodynamic impact is signed as \(x^{\prime }\), for simplicity, hypothesis the deformation is satisfied with the Hooke’s law, then,

$$\begin{aligned} F= & {} k^{\prime }\cdot x^{\prime } \end{aligned}$$
(17)
$$\begin{aligned} x^{\prime }= & {} F/k^{\prime } \nonumber \\= & {} \varDelta \cdot \overline{{ GM }} \cdot \sum _{i=1}^\infty {\pi \frac{h_{i}}{\lambda _{i}}\cos (\omega _{i}t+\varepsilon _{i})} /k^{\prime }\nonumber \\= & {} k_{4}\cdot \sum _{i=1}^\infty {\frac{h_{i}}{\lambda _{i}}\cos (\omega _ {i}t+\varepsilon _{i})} \end{aligned}$$
(18)

So, the total deformation can be expressed as:

$$\begin{aligned} X=x+x^{\prime } \end{aligned}$$
(19)

And then, the change of displacement is:

$$\begin{aligned} \delta \varDelta= & {} k_{1}\cdot X\cdot \tan \varphi \nonumber \\= & {} k_{1}\cdot (x+x^{\prime })\cdot \tan \varphi \nonumber \\= & {} k_{1}\cdot x\cdot \tan \varphi +k_{1}\cdot x^{\prime }\cdot \tan \varphi \nonumber \\= & {} k_{1}\cdot k_{3}\cdot u_F^2 \cdot \tan \varphi +k_{1}\cdot k_{4}\cdot \sum _{i=1}^\infty {\frac{h_{i}}{\lambda _{i}}\cos (\omega _{i}t+\varepsilon _{i})} \nonumber \\= & {} K_{1}\cdot u_F^2 \cdot \tan \varphi +K_{2}\cdot \tan \varphi \cdot \sum _{i=1}^\infty {\frac{h_{i}}{\lambda _{i}}\cos (\omega _{i}t+\varepsilon _{i})}\nonumber \\ \end{aligned}$$
(20)

Thus, when the wind and waves coupling is considered, the completed boat rolling motion equation is written as

(21)

where \(K_1\), \(K_2\) are constant numbers to a specific boat.

3 Numerical simulation

3.1 The deformation is caused only by wind

Simulation parameters are given as: Boat length L is 11.4 m, type wide B is 2.51 m, deep D is 1.305 m, initial stability height \(\overline{{ GM }}\) is 0.707 m, design draft d is 0.60 m, drainage volume V is 8.14 cubic meters, displacement \(\varDelta \) is 8.34 tons, distance \(Z_{g}\) between gravity center and midline is 0.304 m, wind area S is 9.26 \(\hbox {m}^2\), height H between wind pressure center and water surface is 0.882 m, no-load weight is 2.9 tons, and full load weight is 8.34 tons. The stability vanish angle \(\varphi \gamma \) is 1.57 rad. The area \(A\varphi \) surrounded by static stability curve and stability vanish angle is \(0.4112\,\hbox {m}\,\hbox {rad}\). Take the air density \(\rho _\mathrm{air}=1.2\,\hbox {kg/m}^{3}\) and the effective coefficient of slope \(\alpha _0=0.729\). Consider full load condition. The total rotation moment of inertia is \(1.820 t\, \hbox {m}^{2}\). The coherent roll frequency \(\omega _0=1.80\,\hbox {rad/s}\). Damping coefficient \(D_1=0.04002\) and \(D_3=0.027288\). Restoring factor \(C_3=-0.3352\) and \(C_5=0.019608\). Restoring moment is only calculated up to the 5-power term \(\varphi ^{5}\). Integrated deformation coefficient \(K_1=0.1\), \(K_2=0\). Waves are regular ones. The significant sea wave height, wavelength and wave frequency are \(h=3\,\hbox {m}\), \(\lambda =90\,\hbox {m}\) and \(\omega =0.85\hbox {rad}/\hbox {s}\), respectively. Also assume that there is no navigational speed and only beam wind with speed \(u_F =10+10\cos (4t)\) is considered. Take the aforementioned parameter values into Eq. 21 and get boat rolling motion equation as follows

$$\begin{aligned}&1.82{\ddot{\varphi }}+0.04002{\dot{\varphi }}+0.027288{\dot{\varphi }}^{3} \nonumber \\&\qquad +(8.34+0.1^{*}(10+10\cos (4t))^{2}\cdot \tan \varphi ) \nonumber \\&\qquad \cdot (0.707\varphi -0.3352\varphi ^{3}+0.019608\varphi ^{5}) \nonumber \\&\quad =0.45\cos (0.85t)+6.567(10+10\cos (4t))^{2} \end{aligned}$$
(22)

Let \(x=\varphi ,y=\dot{\varphi }\), then Eq. 22 becomes

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}=y \\ \dot{y}=-0.022y-0.015y^{3}-(4.5824+0.055\\ \qquad \; \cdot (10+10\cos (4t))^{2}\cdot \tan x) \\ \qquad \; \cdot (0.707x-0.3352x^{3}+0.019608x^{5}) \\ \qquad \; +\,0.25\cos (0.85t)+3.608(10+10\cos (4t))^{2} \\ \end{array}}\right. \nonumber \\ \end{aligned}$$
(23)

Next, we discuss how the rolling motion changes when deformation coefficient \(K_{1}\), wind frequency and wave frequency are modified. We set wind frequency to 4 rad/s and wave frequency to 0.85 rad/s. The initial condition \((x_{0},\,y_{0})=(0,\,0)\). We get waveform diagrams as shown in Figs. 4 and 5. We find that the roll angle decreases with the increasing of \(K_{1}\). On the contrary, the roll angular velocity increases with the decreasing of \(K_{1}\).

Fig. 4
figure 4

Roll angle curves changing with time for different coefficient \(K_{1}\) under \(K_{2}=0\)

Full size image
Fig. 5
figure 5

Roll angle velocity curves changing with time for different coefficient \(K_{1}\) under \(K_{2}=0\)

Full size image

3.2 The deformation is caused by the coupling of wind and waves

When the wind and waves coupling is considered, hypothesis the other parameters are the same as the former, let \(K_{1}=K_{2}=0.1\), then the roll motion Eq. (21) will become:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}=y \\ \dot{y}=-0.022y-0.015y^{3}-(4.5824 \\ \qquad \; +\,0.055(10+10\cos (4t))^{2}\cdot \tan x \\ \qquad \; +\,0.002\tan x\cdot \cos (0.85t))\cdot (0.707x \\ \qquad \; -\,0.3352x^{3}+0.019608x^{5})+0.25\cos (0.85t) \\ \qquad \; +\,3.608(10+10\cos (4t))^{2} \\ \end{array}}\right. \end{aligned}$$
(24)

Under different \(K_{1}\), \(K_{2}\), the roll angle and roll angular velocity curve are shown in Figs. 6 and 7. Through observed, it is found that the roll angular velocity varied intensely and strengthened along with the \(K_{1}\), \(K_{2}\) increase.

Fig. 6
figure 6

Roll angle curves changing with time for different coefficient \(K_{1}\), \(K_{2}\)

Full size image
Fig. 7
figure 7

Roll angle velocity curves changing with time for different coefficient \(K_{1}\), \(K_{2}\)

Full size image

3.3 Validation of the chaos characteristic

The simulation parameters are the same as the former, consider the deformation is caused by the wind and waves coupling.

Further study finds that system (24) may appear to be chaotic with the change of \(K_{1}\), \(K_{2}\). For example, when \(K_{1}=0.005\), \(K_{2}=0.005\), the Lyapunov exponential is (0.0115, \(-\)0.0146, 0) by using the Gram–Schmit orthogonal method. Figure 8 shows its Lyapunov exponential spectrum, and Fig. 9 shows its phase graph. There exists positive Lyapunov exponential. It indicates that the system is in chaotic state.

Fig. 8
figure 8

Lyapunov exponential spectrum of system (24) under \(K_{1}=0.005\), \(K_{2}=0.005\)

Full size image

It is well known to all that Poincare map is a good kind of tool to distinguish chaos. The map of periodic motion is a finite number of discrete points, and the standard periodic motion is a closed curve; the map of chaotic motion is a number of collection of points along with a line segment or a curve, and this collection of points has self-similar fractal structure [9].

Fig. 9
figure 9

Phase graph of \(\varphi -\varphi ^{{\prime }}\) of system (24) under \(K_{1}=0.005\), \(K_{2}=0.005\)

Full size image

The simulation parameters are the same as the former, considered the deformation is caused by the wind and waves coupling. Set \(K_1=0.005,K_2=0.005\), the Poincare map of system (24) is shown as Fig. 10, and obviously, the system is chaotic.

Fig. 10
figure 10

Poincare map of system (24) under \(K_{1}=0.005\), \(K_{2}=0.005\)

Full size image

The above simulation result shows that the rolling will get more intense and the stability will get weakened when boat deformation is considered. At the same time, the ride comfort will get worse too. In particular, the appearance of chaos may increase the danger of the boat [23]. So it is necessary to control chaos when boat deformation is considered.

3.4 Control of chaos

With regard to the chaos control of boat rolling, document [24] achieved satisfactory results by using nonlinear simple control method which is the combination of the accurate feedback linearization method and the closed-loop gain shaping algorithm to get rid of the boat chaotic state. Here, we use this method. Add a control item u to the second equation of system (24). Then, we get a controlled system (25):

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}=y \\ \dot{y}=-0.022y-0.015y^{3}-(4.5824 \\ \qquad \; +\,0.055(10+10\cos (4t))^{2}\cdot \tan x \\ \qquad \; +\,0.002\tan x\cdot \cos (0.85t))\cdot (0.707x \\ \qquad \; -\,0.3352x^{3}+0.019608x^{5})+0.25\cos (0.85t) \\ \qquad \; +\,3.608(10+10\cos (4t))^{2}+u \\ \end{array}} \right. \end{aligned}$$
(25)

According to the nonlinear simple control method based on the algorithm of accurate feedback linearization, u can be expressed as

$$\begin{aligned} \begin{array}{l} u=0.022y+0.015y^{3}+(4.5824 \\ \qquad \;+\,0.055(10+10\cos (4t))^{2}\cdot \tan x \\ \qquad \;+\,0.002\tan x\cdot \cos (0.85t))\cdot (0.707x \\ \qquad \;-\,0.3352x^{3}+0.019608x^{5})-0.25\cos (0.85t) \\ \qquad \;-\,3.608(10+10\cos (4t))^{2}+v \\ \end{array} \end{aligned}$$
(26)

Using the method in document [24], we obtain a PD controller \(v=-6x-3y\). So the whole control law is

$$\begin{aligned} \begin{array}{l} u=0.022y+0.015y^{3}+(4.5824 \\ \qquad \; +\,0.055(10+10\cos (4t))^{2}\cdot \tan x \\ \qquad \; +\,0.002\tan x\cdot \cos (0.85t))\cdot (0.707x \\ \qquad \; -\,0.3352x^{3}+0.019608x^{5})-0.25\cos (0.85t) \\ \qquad \; -\,3.608(10+10\cos (4t))^{2}-6x-3y \\ \end{array} \end{aligned}$$
(27)

In order to compare the effects before and after the control, the condition of wind speed and sea waveform is given as below

$$\begin{aligned} \left\{ {\begin{array}{l} 0\le t<5s: \\ uF=10+10\cos (4t),\zeta (t)=\frac{3}{15}\cos (2t); \\ 5\le t<10s: \\ uF=15+10\cos (4t)+5\cos (8t), \\ \zeta (t)=\frac{3}{15}\cos (2t)+\frac{10}{3.8}\cos (4t); \\ 10\le t<15s: \\ uF=17+10\cos (4t)+5\cos (8t)+2\cos (12t), \\ \zeta (t)=\frac{3}{15}\cos (2t)+\frac{10}{3.8}\cos (4t)+\frac{15}{1.71}\cos (6t) \\ \end{array}} \right. \end{aligned}$$
(28)

Set \(K_{1}=K_{2}=0.1\). Other parameters are the same as before. Add the controlling item u when \(t=15\hbox {s}\), end the control when \(t=20\hbox {s}\). The phase graph of system (25) is shown in Fig. 11. After being controlled, the system gets rid of chaos and is controlled at the equilibrium point (0, 0).

Fig. 11
figure 11

Phase graph of the controlled system (25)

Full size image

3.5 Analysis of robustness

A controlled system is robust if it meets that (1) it has a low sensitivity; (2) the system is always stable within the scope of the parameters may change; (3) the performance of the system can meet the requirements when the parameters change [25–27].

In fact, a real controlled system often exists model error and measurement noise, and an effective control strategy must have strong robustness. The robustness of the controlled system (25) is analyzed as follows.

Firstly, when the system exists model error, we set the wind frequency 4, 8, 12 rad/s, respectively, in different times as expression (28), add the control strategy u at 15 s, and end it at 20 s, and the roll angle curves changing with time of the controlled system (25) are shown in Fig. 12. From Fig. 12, we find the control strategy u can control the system very well even though there exists model error.

Fig. 12
figure 12

Roll angle curves changing with time of the controlled system (25) when exists model error

Full size image

Secondly, when the system exists measurement noise, we add white noise enoise to the controlled system (25).

Here,

$$\begin{aligned} enoise=\psi (T)\cdot \sin (\varpi T) \end{aligned}$$
(29)

where

$$\begin{aligned} \psi (T)= & {} 0.05\pm 0.002r(T) \end{aligned}$$
(30)
$$\begin{aligned} \varpi (T)= & {} 0.5\pm 0.02r(T) \end{aligned}$$
(31)

and r(T) is a normally distributed random function [25]. Add the control strategy u from 15 to 50 s, and the time response curve of roll angle of the controlled system (25) is shown in Fig. 13.

Fig. 13
figure 13

Roll angle curves changing with time of the controlled system (25) when exists measurement noise

Full size image

At last, when the system exists both model error and measurement noise, the other simulation parameters are the same as the former and the model error and the enoise are the same as the former too. The time response curve of roll angle of the controlled system (25) is shown in Fig. 14.

Fig. 14
figure 14

Roll angle curves changing with time of the controlled system (25) when exists both model error and measurement noise

Full size image

The simulation shows that the designed controller has good control effect, and the controlled system (25) is robust when the system is subject to parameter uncertainties and noise measurement.

3.6 Comparison with previously published work

The literature that specially researches the stability of rotary-molded boat or rubber boat is very less. Even though there is a few of references which considered its elastic deformation to study the dynamic characteristics of rolling of the rotary-molded boat, the research object of them is the steel ship. Compared with the references [6, 8, 9], the main work of our study can be stated as the following several aspects: (1) The modeling method of us considered the wind and waves coupling, which is closer to the actual situation; (2) the simulation shows that the rolling angular velocity and angular acceleration will increase when considering the deformation of boat; at this time, the ship’s stability deserves more attention; (3) when considering its elastic deformation, the stability of boat will decrease, but regarding how to accurately calculate and evaluate how much of the stability decreased, as well how to improve the stability, neither the references nor we consider it; this is our future research direction.

4 Conclusions

In this paper, we take a rotary-molded boat as the research object. We first consider the hull’s deformation to establish a nonlinear rolling equation. From simulations, it is shown that the stability gets weakened and the system gets chaotic when elastic deformation is considered. In detail, the investigation leads to the following conclusions:

  1. (1)

    The rotary-molded boat has complex dynamic characteristics when the irregular wind and wave act on it.

  2. (2)

    Along with the increase in wind and wave harmonic, the influence of the dynamic characteristics of boat is significant. Some simulation methods and results such as the time domain curve, phase diagram, Lyapunov exponential spectrum, as well Poincare map reflect this changes from different aspects.

  3. (3)

    When the elastic deformation of boat is caused by the wind and waves coupling, the rolling is much more intense, its stability will decline further more, and the chaos phenomenon is more obvious.

  4. (4)

    The controlling method is feasible and effective. It can control the system to the balance point. Furthermore, the controller has good robustness.

In addition, the rotary-molded boat technology is a kind of innovation of boat material, and along with the development of social, there will have more and more rotary-molded boats. The rolling movement model which is established by us is much more in line with the actual than the related citations. The research of this paper laid a foundation of improving the design method of boat, and the calculation method can be popularized and applied to other ships. Therefore, it is significant to amend the stability inspection standard to control boat chaos more effectively, which is our research focus in the future too.