Lagrangian Jacobian inverse for nonholonomic robotic systems

Abstract

The motion planning problem for nonholonomic robotic systems is studied using the continuation method and the optimization paradigms. A new Jacobian motion planning algorithm is derived, based on a solution of the Lagrange-type optimization problem addressed in the linear approximation of the system. Performance of the new algorithm is illustrated by numeric computations performed for the unicycle robot kinematics.

1 Introduction

The kinematics of a nonholonomic robotic system subject to Pfaffian phase constraints can be represented in the form of a driftless control system with outputs. The motion planning problem becomes then equivalent to inverting the end point map of this system. An application of the continuation method provides a systematic way of deriving Jacobian motion planning algorithms. In the context of robotics, the continuation method was introduced by Sussmann [16] and then used successfully in the motion planning of mobile robots [6, 7], mobile manipulators [17] and rolling bodies [1, 3], extended to systems with dynamics [10, 13, 19], as well as developed theoretically towards proving completeness (convergence for any initial controls) of Jacobian motion planning algorithms [4, 5, 15, 18], incorporating state and control bounds [9], adopting them to the multiple-task motion planning [11, 13], as well as improving their computational properties [12]. The Jacobian of a nonholonomic system is defined as the end point map in the linear approximation to the original system. An inverse Jacobian is computed as a solution of a constrained optimization problem formulated in this linear approximation. Then, an essential ingredient of the motion planning algorithm is a functional differential equation involving an inverse of the Jacobian. In the cited works, the Jacobian inverse has usually come from the minimization of the control squared norm (energy), resulting in either the Jacobian pseudoinverse (a Moore–Penrose generalized inverse in a Hilbert space [2]) or a weighted Jacobian pseudoinverse.

In this note, using the continuation method, we introduce a new Jacobian inverse for the nonholonomic kinematics. The new inverse is referred to as the Lagrangian Jacobian inverse, as it relies on a constrained minimization of the Lagrange-type objective function. Our main result consists in deriving this new inverse and providing a corresponding motion planning algorithm. Differently to the Jacobian pseudoinverse, the Lagrangian Jacobian inverse incorporates at every step not only the minimization of the control variation, but a joint minimization of both the system control and the system trajectory variations. The computations underlying the algorithm are equivalent to solving a set of differential-algebraic equations. Computability and performance of the Lagrangian Jacobian motion planning algorithm are demonstrated by solving a motion planning problems for the unicycle-type mobile robot. The presented case study suggests that this motion planning algorithm can be designed in such a way that, besides solving the motion planning problem itself, it allows for shaping the system trajectories in order to foster a desired way of motion, e.g. avoiding obstacles.

The remaining part of this note is composed in the following way. Sect. 2 presents the basic concepts, including basics of the continuation method and the concept of the Jacobian pseudoinverse for nonholonomic systems. Section 3 contains our main result, i.e. the Lagrangian Jacobian inverse. The corresponding motion planning algorithm is described in Sect. 4. Computational aspects of the new algorithm are discussed in Sect. 5 in the context of the unicycle robot. Section 6 contains conclusions. Proofs of the main results are given in “Appendix”.

2 Basic concepts

We shall study the kinematics of a nonholonomic robotic system, represented as a driftless control system with outputs

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}=G(q)u=\sum _{i=1}^mg_i(q)u_i,\\ y=k(q), \end{array}\right. \end{aligned}$$

(1)

where $q=(q_1,q_2,\ldots ,q_n)^T\in R^n$ is the state variable, $u=(u_1,u_2,\ldots ,u_m)^T\in R^m$ denotes the control, and $y=(y_1,y_2,\ldots ,y_r)^T\in R^r$ stands for the output variable. All the vector fields and functions appearing in (1) will be assumed smooth (of $C^\infty$ class). The admissible control functions $u(\cdot )\in {\mathcal {U}}\subset L_m^2[0,T]$, where T is a fixed control horizon, belong to a subset of the space of Lebesgue square integrable functions on [0, T], with inner product inherited from the ambient space. It is assumed that for admissible control functions the state trajectory $q(t)=\varphi _{q_0,t}(u(\cdot ))$ exists for every $t\in [0,T]$ and every initial state $q_0\in R^n$. Given a state trajectory, the end point map $K_{q_0,T}:{\mathcal {U}}\longrightarrow R^r$ of the system (1) is defined as

$$\begin{aligned} K_{q_0,T}(u(\cdot ))=k(\varphi _{q_0,T}(u(\cdot ))). \end{aligned}$$

(2)

It is well known that the end point map of the system (1) is continuously differentiable [14]. Its derivative will be referred to as the system’s Jacobian,

$$\begin{aligned}&J_{q_0,T}(u(\cdot ))v(\cdot )={\mathcal {D}}\, K_{q_0,T}(u(\cdot ))v(\cdot )\nonumber \\&\quad =C(T){\mathcal {D}}\,\varphi _{q_0,T}(u(\cdot )) v(\cdot )=\eta (T)=\eta , \end{aligned}$$

(3)

for $u(\cdot ),v(\cdot )\in {\mathcal {U}},$ and $\eta (t)$ denote the output trajectory of the linear approximation to (1) along (u(t), q(t)). Letting

$$\begin{aligned} \xi (t)={\mathcal {D}}\,\varphi _{q_0,t}(u(\cdot ))v(\cdot ), \end{aligned}$$

(4)

we get [17]

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\xi }=A(t)\xi +B(t)v,\\ \eta (t)=C(t)\xi , \end{array}\right. \end{aligned}$$

(5)

where $A(t)=\frac{\partial G(q(t))u(t)}{\partial q}$, $B(t)=G(q(t))$, and $C(t)=\frac{\partial k(q(t))}{\partial q}$. Then, after solving (5) for $\xi (0)=0$, the Jacobian (3) can be expressed as

$$\begin{aligned} J_{q_0,T}(u(\cdot ))v(\cdot )=C(T)\int _0^T\,\varPhi (T,t)B(t)v(t)\hbox {d}t, \end{aligned}$$

(6)

with the transition matrix $\varPhi (t,s)$ satisfying the evolution equation

$$\begin{aligned} \frac{\partial \varPhi (t,s)}{\partial t}=A(t)\varPhi (t,s), \end{aligned}$$

(7)

along with $\varPhi (s,s)=I_n$, the identity matrix.

Using the kinematics representation (1), we shall study the following motion planning problem of a nonholonomic robotic system: given an initial state $q_0\in R^n$ and a terminal point $y_d\in R^r$, find a control function $u(\cdot )\in {\mathcal {U}}$ such that

$$\begin{aligned} K_{q_0,T}(u(\cdot ))=y_d. \end{aligned}$$

(8)

This motion planning problem can be solved by means of a Jacobian algorithm whose derivation goes along the following lines. We begin with an arbitrary control function $u_0(\cdot )\in {\mathcal {U}}$. If it solves the problem, we are done. Otherwise, we introduce a deformation of $u_0(\cdot )$ into a smooth curve $u_{\theta }(\cdot )\in {\mathcal {U}}$, $\theta \in R$, such that $u_{\theta =0}(\cdot )=u_0(\cdot )$, and compute the motion planning error $e(\theta )=K_{q_0,T}(u_{\theta }(\cdot ))-y_d$ along this curve. Requesting that the error decreases exponentially,

$$\begin{aligned} \frac{d e(\theta )}{d\theta }=-\gamma e(\theta ),\quad \gamma >0, \end{aligned}$$

(9)

we arrive at Ważewski–Davidenko equation

$$\begin{aligned} J_{q_0,T}(u_{\theta }(\cdot ))\frac{d u_{\theta }(\cdot )}{d\theta }=-\gamma (K_{q_0,T}(u_{\theta }(\cdot ))-y_d), \end{aligned}$$

(10)

involving the Jacobian (3). This equation can be made explicit after employing a right inverse $J_{q_0,T}^{\#}(u(\cdot )):R^r\longrightarrow {\mathcal {U}}$ of the Jacobian, so that

$$\begin{aligned} \frac{d u_{\theta }(\cdot )}{d\theta }=-\gamma J_{q_0,T}^{\#}(u_{\theta }(\cdot ))(K_{q_0,T}(u_{\theta }(\cdot ))-y_d). \end{aligned}$$

(11)

By design, the control function driving the system (1) in the initial state $q_0$ to $y(T)=y_d\in R^r$ is computed as the limit

$$\begin{aligned} u(t)=\lim _{\theta \rightarrow +\infty }u_\theta (t). \end{aligned}$$

The right Jacobian inverse is usually obtained by solving for $v(\cdot )\in {\mathcal {U}}$ a Jacobian equation

$$\begin{aligned} J_{q_0,T}(u(\cdot ))v(\cdot )=\eta . \end{aligned}$$

(12)

Specifically, the Jacobian equation may be attached as an equality constraint to the energy minimization problem in the linearization (5),

$$\begin{aligned} \min _{v(\cdot )} \int _0^T\,v^T(t)v(t)\hbox {d}t, \end{aligned}$$

(13)

on condition that

$$\begin{aligned} J_{q_0,T}(u(\cdot ))v(\cdot )=C(T)\xi (T)=\eta , \end{aligned}$$

that results in the Jacobian pseudoinverse [17]

$$\begin{aligned}&\left( J_{q_0,T}^{P\#}(u(\cdot ))\eta \right) (t)= v(t)\nonumber \\&\quad =B^T(t)\varPhi ^T(T,t)C^T(T)\mathcal {G}_{q_0,T}^{-1}\eta , \end{aligned}$$

(14)

where

$$\begin{aligned} \mathcal {G}_{q_0,T}= & {} C(T)\left( \int _0^T\,\varPhi (T,t)B(t) B^T(t)\varPhi ^T(T,t)dt\right) \nonumber \\&\times \, C^T(T) \end{aligned}$$

(15)

is the output controllability Gramian of the system (5). In the mobile robotics context, this Gramian is referred to as the mobility matrix [19]. It follows that the Gramian matrix can be computed by solving the Lyapunov differential equation

$$\begin{aligned} \dot{M}(t)=B(t)B^T(t)+A(t)M(t)+M(t)A^T(t), \end{aligned}$$

(16)

for zero initial condition $M(0)=0$ and setting $\mathcal {G}_{q_0,T}=C(T)M(T)C^T(T)$. If the Gramian (15) is full rank, a straightforward computation shows that the minimal value of the objective function (13) equals $\eta ^T\mathcal {G}^{-1}_{q_0,T}\eta$.

3 Lagrangian Jacobian inverse

As has been said above, a right inverse of the Jacobian (6) can be obtained by solving a constrained optimization problem for the linearization (5) of the original system (1). A natural generalization of the objective function considered in (13) is an objective function in the Lagrange form that leads to the Lagrange-type optimization problem in (5)

$$\begin{aligned} \min _{v(\cdot )}\int _0^T\,\left( \xi ^T(t)Q(t)\xi (t) +v^T(t)R(t)v(t)\right) \hbox {d}t, \end{aligned}$$

(17)

along with

$$\begin{aligned} J_{q_0,T}(u(\cdot ))v(\cdot )=C(T)\xi (T)=\eta , \end{aligned}$$

where the matrices $Q(t)=Q^T(t)\ge 0$ and $R(t)=R^T(t)>0$. The resulting Jacobian inverse will be referred to as the Lagrangian Jacobian inverse $J^{L\#}_{q_0,T}(u(\cdot ))$. The following theorem establishes the explicit form of the Lagrangian Jacobian inverse. Its proof can be found in Proof of Theorem 1 in “Appendix”.

Theorem 1

The Lagrangian Jacobian inverse

$$\begin{aligned} \left( J^{L\#}_{q_0,T}(u(\cdot ))\eta \right) (t)=v(t)=-R^{-1}(t) B^T(t)L(T,t,\eta ), \end{aligned}$$

(18)

where

$$\begin{aligned}&L(T,t,\eta )= -\psi _{22}(t)\left( \psi _{22}(T)+C^T(T)\right. \nonumber \\&\quad \left. \mathcal {M}_{q_0,T}^{-1}C(T) \psi _{32}(T)\right) ^{-1} C^T(T)\mathcal {M}_{q_0,T}^{-1}\eta , \end{aligned}$$

(19)

and the block matrix function $\varPsi (t)=[\psi _{ij}(t)]$, $i,j=1,2,3$ solves the linear differential equation

$$\begin{aligned} \dot{\varPsi }(t)= & {} \left[ \begin{array}{ccc} \dot{\psi }_{11}(t)&{}\dot{\psi }_{12}(t)&{}\dot{\psi }_{13}(t)\\ \dot{\psi }_{21}(t)&{}\dot{\psi }_{22}(t)&{}\dot{\psi }_{23}(t)\\ \dot{\psi }_{31}(t)&{}\dot{\psi }_{32}(t)&{}\dot{\psi }_{33}(t) \end{array}\right] \nonumber \\= & {} \left[ \begin{array}{ccc} A(t)&{}-B(t)R^{-1}(t)B^T(t)&{}0\\ -Q(t)&{}-A^T(t)&{}0\\ D(t)Q(t)&{}0&{}A(t)\end{array}\right] \varPsi (t),\nonumber \\ \end{aligned}$$

(20)

with initial condition $\psi _{ij}(0)=\delta _{ij}I_n$, $\delta _{ij}$ denoting the Kronecker delta. The matrix D(t) is a solution of the Lyapunov equation

$$\begin{aligned} \dot{D}(t)=B(t)R^{-1}(t)B^T(t)+A(t)D(t)+D(t)A^T(t), \end{aligned}$$

(21)

with zero initial condition $D(0)=0$, and the mobility matrix

$$\begin{aligned} \mathcal {M}_{q_0,T}=C(T)D(T)C^T(T). \end{aligned}$$

(22)

The mobility matrix will be assumed to have full rank r. It is easily shown that, after setting $Q(t)=0$ and $R(t)=I_m$, the Lagrangian Jacobian inverse and the Jacobian pseudoinverse coincide. This is stated as

Corollary 1

If $Q(t)=0$ and $R(t)=I_m$, then $J^{L\#}_{q_0,T}(u(\cdot ))=J^{P\#}_{q_0,T}(u(\cdot )).$

This corollary will be demonstrated in Proof of Corollary 1 in “Appendix”. By inspection of the differential equation (20), we obtain the next

Corollary 2

In the block matrix $\varPsi (t)$, the terms $\psi _{13}(t)$ and $\psi _{23}(t)$ are zero.

Suppose that the output function of (1) is the identity function $k(q)=q$. Then, we have the following

Corollary 3

$$\begin{aligned} L(T,t,\eta )=\psi _{22}(t)\psi _{12}^{-1}(T)\eta . \end{aligned}$$

(23)

Proof of this Corollary can be found in Proof of Corollary 3 in ”Appendix”.

4 Motion planning

The Lagrangian Jacobian inverse gives rise to a Lagrangian Jacobian motion planning algorithm based on the scheme (11) with $J^{\#}_{q_0,T}(u(\cdot ))$ replaced by $J^{L\#}_{q_0,T}(u(\cdot ))$, see (18). The computations involved in this algorithm are tantamount to solving for $u_{\theta }(t)$ the following set of differential-algebraic equations.

Algorithm 1

$$\begin{aligned} \left\{ \begin{array}{l} \begin{array}{l} \dot{q}_\theta (t)=G(q_\theta (t))u_\theta (t), \\ \dot{D}_\theta (t)=B_\theta (t)R^{-1}(t)B^T_\theta (t)+A_\theta (t)D_\theta (t)+D_\theta (t)A^T_\theta (t),\end{array}\\ \begin{array}{l} \dot{\varPsi }_\theta (t)= \left[ \begin{array}{ccc} A_\theta (t)&{}-B_\theta (t)R^{-1}(t)B^T_\theta (t)&{}0\\ -Q(t)&{}-A^T_\theta (t)&{}0\\ D_\theta (t)Q(t)&{}0&{}A_\theta (t)\end{array}\right] \varPsi _\theta (t), \end{array}\\ \begin{array}{l} \frac{\hbox {d}u_\theta (t)}{\hbox {d}\theta }= -\gamma R^{-1}(t)B^T_\theta (t)\psi _{\theta 22}(t)\\ \left( \psi _{\theta 22}(T)+C^T_\theta (T)\mathcal {M}_{q_0,T}^{-1}(\theta )\right. \\ \left. \qquad C_\theta (T)\psi _{\theta 32}(T)\right) ^{-1} C^T_\theta (T)\mathcal {M}_{q_0,T}^{-1}(\theta )e(\theta ), \end{array}\quad (\dagger )\\ \begin{array}{l} A_\theta (t)=\frac{\partial (G(q_\theta (t))u_\theta (t))}{\partial q},\, B_\theta (t)=G(q_\theta (t)),\, C_\theta (t)\\ \qquad =\frac{\partial k(q_\theta (t))}{\partial q}, \end{array} \\ \begin{array}{l} \mathcal {M}_{q_0,T}(\theta )=C_\theta (T)D_\theta (T)C^T_\theta (T),\\ e(\theta )=y_\theta (T)-y_d=k(q_\theta (T))-y_d, \end{array} \end{array} \right. \end{aligned}$$

with initial conditions $q_\theta (0)=q_0$, $D_\theta (0)=0$, $\psi _{\theta ij}(0)=\delta _{ij}I_n$ and a given initial control function $u_0(t)$.

As explained in Sect. 2, the solution of the motion planning problem is obtained as the limit

$$\begin{aligned} u(t)=\lim _{\theta \rightarrow +\infty }u_\theta (t). \end{aligned}$$

5 Computer simulations

An advantage of the Lagrangian Jacobian motion planning algorithm is that by a suitable choice of matrices Q(t) and R(t) defining the Lagrange objective function (17), besides solving the motion planning problem itself, it also enables shaping the state trajectory of the system (1).

For a given $\theta$, suppose that $v_{\theta }(\cdot )$ is the solution of the Jacobian equation

$$\begin{aligned} J_{q_0,T}(u_{\theta }(\cdot ))v_{\theta }(\cdot )= K_{q_0,T}(u_{\theta }(\cdot ))-y_d \end{aligned}$$

(24)

obtained by means of the Lagrangian Jacobian inverse. By (11) and (18) with a substitution $\eta =e(\theta )$, this means that

$$\begin{aligned} \frac{\hbox {d} u_{\theta }(t)}{\hbox {d}\theta }=-\gamma v_{\theta }(t). \end{aligned}$$

(25)

Furthermore, let $q_{\theta }(t)=\varphi _{q_0,t}(u_{\theta }(\cdot ))$ be the state trajectory of the control system (1) steered by $u_{\theta }(t)$. Then, the identity (4) combined with (25) yields

$$\begin{aligned}&\frac{\hbox {d} q_{\theta }(t)}{\hbox {d}\theta }={\mathcal {D}}\varphi _{q_0,t}(u_{\theta }(\cdot ))\frac{\hbox {d} u_{\theta }(\cdot )}{\hbox {d}\theta }\nonumber \\&\quad =-\gamma {\mathcal {D}}\varphi _{q_0,t}(u_{\theta }(\cdot ))v_{\theta }(\cdot )=-\gamma \xi _{\theta }(t). \end{aligned}$$

(26)

The functions $v_\theta (\cdot )$ and $\xi _\theta (\cdot )$ can be interpreted as directions of motion in the control and trajectory spaces.

For a curve $c_\theta (t)$ in the state space of system (1), let $V_\theta (t)$ denote a vector field along $c_\theta (t)$. The matrix Q(t) can be made $\theta$ dependent, so we set

$$\begin{aligned} Q_\theta (t)=V_\theta (t)V^T_\theta (t). \end{aligned}$$

Then, for a fixed $\theta$, the Lagrange objective function (17) becomes equal to

$$\begin{aligned} \int _0^T\,\left( \left( \xi _\theta ^T(t)V_\theta (t)\right) ^2+ v^T_\theta (t)R_\theta (t)v_\theta (t)\right) dt, \end{aligned}$$

(27)

where we have also allowed for the matrix R(t) to depend on $\theta$. With a suitable choice of the vector field $V_\theta (t)$ and the matrix $R_\theta (t)$, the minimization of this objective function will make the direction of motion $\xi _\theta (\cdot )$ orthogonal to $V_\theta (\cdot )$ at each t. It might be expected that, by an appropriate choice of the matrices Q(t) and R(t), it could be possible to shape the solution of the motion planning problem, e.g. in order to enable avoiding obstacles in the state space of the system (1).

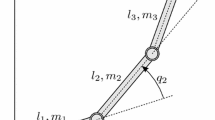
In the remaining part of this section, we shall verify this expectation by numerically solving a motion planning problem for the unicycle-type mobile robot. The robot is shown schematically in Fig. 1.

Fig. 1

The unicycle

Under assumption that the wheel is not permitted to slip laterally, its kinematics are represented by a driftless control system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}=\left[ \begin{array}{c@{\quad }c} \cos q_3 &{} 0\\ \sin q_3 &{} 0\\ 0 &{} 1 \end{array}\right] \left( \begin{array}{l} u_1\\ u_2 \end{array}\right) ,\\ y=k(q)=q, \end{array}\right. \end{aligned}$$

with the state variable $q=(q_1,q_2,q_3)^T\in R^3$ denoting the wheel’s position and orientation (see the figure), a pair of controls $u_1$, $u_2$ denoting the linear and the angular velocity of the wheel and the identity output function. Suppose that the unicycle placed at a given initial state $q_0$ should move to a desired point $y_d$, simultaneously avoiding state space point–obstacles

$$\begin{aligned} O=\{o_1,\ldots ,o_p\}=\{(q^1_1,q^1_2,q^1_3),\ldots ,(q^p_1,q^p_2,q^p_3)\}. \end{aligned}$$

Let for a certain $\theta$ the trajectory of the unicycle be $q_\theta (t)$. Along this trajectory, we define a vector field

$$\begin{aligned} V_\theta (t)=\sum _{i=1}^pV_{i\theta }(t), \end{aligned}$$

where

$$\begin{aligned} V_{i\theta }(t)=C\mathrm {R}(Z,\pi /2)\frac{o_i - q_\theta (t)}{||o_i - q_\theta (t)||}. \end{aligned}$$

The fractional term in the above expression is a direction pointing from the trajectory towards the obstacle number i, while $\mathrm {R}(Z,\pi /2)$ denotes the rotation matrix around the Z axis by the angle $\pi /2$. In order to deal only with position obstacles, the matrix is set to $C=\left[ \begin{array}{cc}I_2&{}0\\ 0&{}0\end{array}\right]$. For a vector field so defined, the minimization of the Lagrange objective function (27) will result in making $\xi _\theta (t)$ orthogonal to $V_\theta (t)$, i.e. repelling the trajectory $q_\theta (t)$ from the obstacles.

This idea will be illustrated with solving numerically a motion planning problem for the unicycle, characterized by the initial state $q_0=(0,0,0)$, the desired point $y_d=q_d=(1,1,0)$, and the set of three obstacles ($p=3$) to be specified later on. The control horizon is set to $T=2$, and the decay rate in the Algorithm 1 is chosen as $\gamma =3$. The computations run until the error norm $||e(\theta )||$ drops below $10^{-4}$. The initial control function is chosen as $u_0=(0.5,\sin (2\pi t/T))$. In order to effectively visualize the algorithm performance, the obstacles will be added progressively. Firstly, we solve the motion planning problem without any obstacles setting $Q_\theta (t)=10^2 I_3$. Next, we will place the first obstacle $o_1$ directly on the trajectory obtained form the previous simulation, so we obtain the matrix $Q_\theta (t)=10^2 V_{1\theta }(t)V^T_{1\theta }(t)$. After that, we will add a second obstacle $o_2$ which will be placed exactly on the trajectory resulting from the former computation, $Q_\theta (t)=10^2\left( V_{1\theta }(t)V^T_{1\theta }(t)+ V_{2\theta }(t)V^T_{2\theta }(t)\right)$. Finally, having added the last obstacle $o_3$, we solve the motion planning problem with three obstacles $O=\{(0.25,0.18,*),(0.8,0.35,*),(1.25,0.84,*)\}$, such that $Q_\theta (t)=10^2V_{\theta }(t)V^T_{\theta }(t)$, where $*$ means that the orientation coordinate is not important.

Results of the computer simulation are displayed in Figs.  2, 3, 4 and 5.

Fig. 2

Path in ($y_1,y_2$)-plane

Fig. 3

Control $u_1(t)$

Fig. 4

Control $u_2(t)$

Fig. 5

Algorithm convergence

In Figs. 2, 3, 4, the dotted line corresponds to the computation without the obstacles, the thick solid line is the final solution for all obstacles, and the thin solid lines represent the intermediate solutions. Figure 2 reveals how the consecutive addition of the obstacles affects the solutions. Figures 3, 4 show the control function for each solution. The algorithm convergence is depicted in Fig. 5, and it can be seen that the pre-assumed decay rate $\gamma =3$ has been maintained.

Algorithm 1 can be run either in a parametric or in a nonparametric mode [11]. In the former case, a finite-dimensional representation of the control functions is used, i.e. by truncated trigonometric series. The computations accomplished in this note follow the nonparametric mode and employ a built-in MATLAB variable step, higher-order ODE solver. Such an approach provides a very high accuracy of computations at the expense of the computation time. In the presented example, in every step of the motion planning algorithm, solving the differential equation ($\dagger$) for all t and a single value of $\theta$ takes about 0.5 s on a 3.2 GHz PC. In order to solve the whole motion planning problem, it is necessary to perform about 100 steps that requires a total computation time around 1 min. As long as we are solving a motion planning problem, this is tolerable because the computations can be done offline. These computations might be accelerated by relaxing accordingly the accuracy requirement and passing to the parametric mode. For real-time control, e. g. for the tracking of a trajectory planned offline, the predictive control algorithm may be recommended, supported with the computational tools of ACADO  [8].

6 Conclusion

A contribution of this note is the Lagrangian Jacobian inverse, and the corresponding motion planning algorithm for nonholonomic robotic systems, based on the continuation method and the optimization paradigm. This inverse has been designed by a joint minimization of variations of the system control and the system trajectory. Computability of the new algorithm has been shown on a simple example of unicycle. The outcomes of computations suggest that employing the Lagrange objective function in the definition of the Jacobian inverse offers new possibilities of shaping the resulting plan of motion, e.g. in order to avoid obstacles. A systematic examination of these possibilities will be a subject of our future work. Another open area for future research is the problem of existence (singularities) and completeness (global convergence) of the Lagrangian Jacobian motion planning algorithm, both in the form presented in this note as well as in a singularity robust version. As in the case of the classical inverse ($Q(t)=0$), a version of the Algorithm 1 respecting control and configuration constraints can be derived. Last but not least, an important issue will be concerned with the organization of computations supporting Algorithm 1 that would balance the accuracy and the efficiency. Although designed basically for driftless control systems representing the nonholonomic robot kinematics, the Lagrangian Jacobian motion planning algorithm can be extended in a natural way to nonholonomic robotic systems with dynamics, represented by control affine systems.

Appendix

1.1 Proof of Theorem 1

In order to solve the optimization problem (17), we shall use the method of the calculus of variations. First, we define the Lagrange function associated with the problem

$$\begin{aligned}&{\mathcal {L}}(v(\cdot ),\lambda )=\int _0^T\,\left( \xi ^T(t)Q(t)\xi (t)+v^T(t)R(t)v(t)\right) \hbox {d}t\nonumber \\&\quad +\, \lambda ^T C(T)\int _0^T\,\varPhi (T,t)B(t)v(t)\hbox {d}t, \end{aligned}$$

(28)

where $\xi (t)=\int _0^t\varPhi (t,s)B(s)v(s)ds$. The derivative of the Lagrange function for $w(\cdot )\in {\mathcal {U}}$ is computed as follows

$$\begin{aligned}&{\mathcal {D}}{\mathcal {L}}(v(\cdot ),\lambda )w(\cdot )=\frac{\hbox {d}}{\hbox {d}\alpha }|_{\alpha =0}{\mathcal {L}}(v(\cdot )+\alpha w(\cdot ),\lambda )\nonumber \\&\quad = 2\int _0^T\left( \int _0^t\xi ^T(t)Q(t)\varPhi (t,s) B(s)w(s)ds\right. \nonumber \\&\qquad \left. +\,v^T(t)R(t)w(t)+\frac{1}{2}\lambda ^TC(T) \varPhi (T,t)B(t)w(t)\right) \mathbf{d}t, \end{aligned}$$

(29)

where $\lambda \in R^r$ denotes a vector of Lagrange multipliers. Using the identity

$$\begin{aligned} \int _0^T\int _0^tf(s,t)\hbox {d}s\hbox {d}t=\int _0^T\int _s^Tf(s,t)\hbox {d}t\hbox {d}s, \end{aligned}$$

we transform (29) to

$$\begin{aligned}&{\mathcal {D}}{\mathcal {L}}(v(\cdot ),\lambda )w(\cdot )\nonumber \\&\quad = 2\int _0^T\left( \int _s^T\xi ^T(t)Q(t)\varPhi (t,s)B(s)\hbox {d}t +v^T(s)R(s)\right. \nonumber \\&\qquad +\,\left. \frac{1}{2}\lambda ^TC(T)\varPhi (T,s)B(s)\right) \,w(s)\hbox {d}s. \end{aligned}$$

(30)

The necessary optimality condition, requesting that for every $w(\cdot )$ the derivative $D{\mathcal {L}}(v(\cdot ),\lambda )w(\cdot )=0$, yields

$$\begin{aligned} v(t)= & {} -R^{-1}(t)B^T(t)\nonumber \\&\times \left( F(T,t)+\frac{1}{2}\varPhi ^T(T,t)C^T(T) \lambda \right) , \end{aligned}$$

(31)

where

$$\begin{aligned} F(t,s)=\int _s^t\varPhi ^T(z,s)Q(z)\xi (z)\hbox {d}z. \end{aligned}$$

(32)

Now, a substitution of (31) to the Jacobian equation (12) allows one to compute $\lambda$ as

$$\begin{aligned} \lambda = -2\mathcal {M}_{q_0,T}^{-1}(\eta +C(T)P(T)), \end{aligned}$$

where

$$\begin{aligned}&\mathcal {M}_{q_0,T}=C(T)\int _0^T\,\varPhi (T,t)B(t) R^{-1}(t)B^T(t)\nonumber \\&\quad \varPhi ^T(T,t)\hbox {d}tC^T(T) \end{aligned}$$

(33)

and

$$\begin{aligned} P(t)=\int _0^t\varPhi (t,s)B(s)R^{-1}(s)B^T(s)F(t,s)\hbox {d}s. \end{aligned}$$

(34)

After the elimination of $\lambda$ from (31), we obtain a preliminary form of the Lagrangian Jacobian inverse

$$\begin{aligned}&\left( J^{L\#}_{q_0,T}(u(\cdot ))\eta \right) (t)=v(t)= -R^{-1}(t)B^T(t)(F(T,t)\\&\quad - \varPhi ^T(T,t)C^T(T)\mathcal {M}_{q_0,T}^{-1}(u(\cdot ))(\eta +C(T)P(T))). \end{aligned}$$

Let us denote the term in brackets on the right-hand side of the above expression as

$$\begin{aligned} L(T,t,\eta )= & {} F(T,t)-\varPhi ^T(T,t)C^T(T)\nonumber \\&\times \,\mathcal {M}_{q_0,T}^{-1}(\eta + C(T)P(T)), \end{aligned}$$

(35)

so that

$$\begin{aligned} \left( J^{L\#}_{q_0,T}(u(\cdot ))\eta \right) (t)= -R^{-1}(t)B^T(t)L(T,t,\eta ). \end{aligned}$$

(36)

This means that (18) holds. On account of

$$\begin{aligned} \frac{\partial \varPhi ^T(T,t)}{\partial t}=-A^T(t)\varPhi ^T(T,t),\quad \varPhi (T,T)=I_n, \end{aligned}$$

[see (7)], a time differentiation of (35) yields

$$\begin{aligned} \frac{\partial L(T,t,\eta )}{\partial t}= & {} \frac{\partial F(T,t)}{\partial t}+ A^T(t)F(T,t)\\&-A^T(t)L(T,t,\eta ). \end{aligned}$$

But from (32), we find

$$\begin{aligned} \frac{\partial F(T,t)}{\partial t}=-Q(t)\xi (t)-A^T(t)F(T,t), \end{aligned}$$

and conclude that

$$\begin{aligned} \begin{array}{l} \frac{\partial L(T,t,\eta )}{\partial t}=-A^T(t)L(T,t,\eta )-Q(t)\xi (t),\\ L(T,T,\eta )= -C^T(T)\mathcal {M}_{q_0,T}^{-1}(\eta + C(T)P(T)). \end{array} \end{aligned}$$

(37)

Eventually, taking into account the formula (34), and the fact that $F(t,t)=0$, we compute

$$\begin{aligned} \dot{P}(t)=A(t)P(t)+D(t)Q(t)\xi (t),\quad P(0)=0, \end{aligned}$$

(38)

where

$$\begin{aligned} D(t)=\int _0^t\varPhi (t,s)B(s)R^{-1}(s)B^T(s)\varPhi ^T(t,s)\hbox {d}s. \end{aligned}$$

It is easily checked that D(t) solves a Lyapunov equation

$$\begin{aligned} \dot{D}(t)=B(t)R^{-1}(t)B^T(t)+A(t)D(t)+D(t)A^T(t), \end{aligned}$$

(39)

with $\quad D(0)=0,$ i. e. the Equation (21) is true. Obviously, the mobility matrix $\mathcal {M}_{q_0,T}=C(T)D(T)C^T(T)$, and hence, also the identity (22) has been proved.

Taking into account the form of (36) as well as (5), (37) and (38), one can observe that in order to compute the Lagrangian Jacobian inverse one needs to solve a set of linear, time-dependent differential equations

$$\begin{aligned} \left( \begin{array}{l}\dot{\xi }(t)\\ \dot{L}(t)\\ \dot{P}(t)\end{array}\right)= & {} \left[ \begin{array}{ccc} A(t)&{}-B(t)R^{-1}(t)B^T(t)&{}0\\ -Q(t)&{}-A^T(t)&{}0\\ D(t)Q(t)&{}0&{}A(t) \end{array}\right] \nonumber \\&\times \left( \begin{array}{l}\xi (t)\\ L(t)\\ P(t)\end{array}\right) , \end{aligned}$$

(40)

where, to simplify notations, we let $L(T,t,\eta )=L(t)$, and $\frac{\partial L(T,t,\eta )}{\partial t}=\dot{L}(t)$.

The system (40) is subject to mixed initial and terminal conditions $\xi (0)=0$, $P(0)=0$, and $L(T)=-C^T(T)\mathcal {M}_{q_0,T}^{-1}(u(\cdot ))(\eta + C(T)P(T))$. Let $\varPsi (t)$ denote the fundamental matrix $\tilde{\varPhi }(t,0)$ of (40). The matrix $\varPsi (t)=[\psi _{ij}(t)]$ satisfies the evolution equation

$$\begin{aligned} \dot{\varPsi }(t)= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c} \dot{\psi }_{11}(t)&{}\dot{\psi }_{12}(t)&{}\dot{\psi }_{13}(t)\\ \dot{\psi }_{21}(t)&{}\dot{\psi }_{22}(t)&{}\dot{\psi }_{23}(t)\\ \dot{\psi }_{31}(t)&{}\dot{\psi }_{32}(t)&{}\dot{\psi }_{33}(t) \end{array}\right] \nonumber \\= & {} \left[ \begin{array}{ccc} A(t)&{}-B(t)R^{-1}(t)B^T(t)&{}0\\ -Q(t)&{}-A^T(t)&{}0\\ D(t)Q(t)&{}0&{}A(t)\end{array}\right] \varPsi (t),\nonumber \\ \end{aligned}$$

(41)

with initial condition $\psi _{ij}(0)=\delta _{ij}I_n$, that is exactly (20). From the equation (41), we deduce

$$\begin{aligned} L(t)= & {} \psi _{21}(t)\xi (0)+\psi _{22}(t)L(0)+\psi _{23}(t)P(0)\nonumber \\= & {} \psi _{22}(t)L(0), \end{aligned}$$

(42)

and in particular,

$$\begin{aligned} L(T)= & {} \psi _{21}(T)\xi (0)+\psi _{22}(T)L(0)+\psi _{23}(T)P(0)\nonumber \\= & {} \psi _{22}(T)L(0). \end{aligned}$$

Furthermore, invoking (37), we get

$$\begin{aligned} \psi _{22}(T)L(0)=-C^T(T)\mathcal {M}_{q_0,T}^{-1}(u(\cdot ))(\eta + C(T)P(T)). \end{aligned}$$

Using again (41), one finds

$$\begin{aligned} P(T)= & {} \psi _{31}(T)\xi (0)+\psi _{32}(T)L(0)+\psi _{33}(T)P(0)\\= & {} \psi _{32}(T)L(0), \end{aligned}$$

therefore

$$\begin{aligned} L(0)= & {} -\left( \psi _{22}(T)+C^T(T)\mathcal {M}_{q_0,T}^{-1}C(T)\psi _{32}(T)\right) ^{-1}\\&\times \, C^T(T)\mathcal {M}_{q_0,T}^{-1}(u(\cdot ))\eta . \end{aligned}$$

Combining the above with (42), we deduce (19). This concludes the proof.

1.2 Proof of Corollary 1

Indeed, if $Q(t)=0$, then (20) implies that

$$\begin{aligned} \dot{\psi }_{22}(t)=-A^T(t)\psi _{22}(t),\quad \psi _{22}(0)=I_n. \end{aligned}$$

Now, because of

$$\begin{aligned} \frac{\partial \varPhi ^T(0,t)}{\partial t}=-A^T(t)\varPhi ^T(0,t),\quad \varPhi (0,0)=I_n, \end{aligned}$$

it follows that $\psi _{22}(t)=\varPhi ^T(0,t)$. Also $\dot{\psi }_{32}(t)=A(t)\psi _{32}(t),\quad \psi _{32}(0)=0,$ so $\psi _{32}(t)=0.$ Taking this into account, and using (19), we deduce that

$$\begin{aligned} L(T,t,\eta )=-\varPhi ^T(T,t)C^T(T)\mathcal {M}_{q_0,T}^{-1}\eta . \end{aligned}$$

But, since $R(t)=I_m$, the definition (15) yields the identity $\mathcal {M}_{q_0,T}=\mathcal {G}_{q_0,T}$.

1.3 Proof of Corollary 3

Since the output matrix $C(T)=I_n$, the term inverted in (19) becomes

$$\begin{aligned}&\psi _{22}(T)+C^T(T)\mathcal {M}_{q_0,T}^{-1}C(T)\psi _{32}(T)\\&\quad =\psi _{22}(T)+D^{-1}(T)\psi _{32}(T). \end{aligned}$$

Consider a matrix

$$\begin{aligned} X(t)=D(t)\psi _{22}(t)+\psi _{32}(t), \end{aligned}$$

and compute its time derivative

$$\begin{aligned} \dot{X}(t)=\dot{D}(t)\psi _{22}(t)+D(t) \dot{\psi }_{22}(t)+\dot{\psi }_{32}(t). \end{aligned}$$

Now, it follows from (20) that

$$\begin{aligned} \dot{\psi }_{22}=-Q(t)\psi _{12}(t)-A^T(t)\psi _{22}(t) \end{aligned}$$

and

$$\begin{aligned} \dot{\psi }_{32}(t)=D(t)Q(t)\psi _{12}(t)+A(t)\psi _{32}(t). \end{aligned}$$

Taking these into account, and after invoking (21), we arrive at a differential equation

$$\begin{aligned} \dot{X}(t)=B(t)R^{-1}(t)B^T(t)\psi _{22}(t)+A(t)X(t), \end{aligned}$$

with the initial condition $X(0)=0$. But, simultaneously, (20) yields

$$\begin{aligned} \dot{\psi }_{12}(t)=-B(t)R^{-1}(t)B^T(t)\psi _{22}(t)+A(t)\psi _{12}(t) \end{aligned}$$

with the same initial condition $\psi _{12}(0)=0$. We conclude that $X(t)=-\psi _{12}(t)$, so

$$\begin{aligned}&\psi _{22}(T)+D^{-1}(T)\psi _{32}(T)=D^{-1}(T)X(T)\\&\quad =-D^{-1}(T)\psi _{12}(T). \end{aligned}$$

Finally, a substitution of the above to (19) results in (23).