Skip to main content
SpringerLink
Log in

On the analytical solutions of the Hindmarsh–Rose neuronal model

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

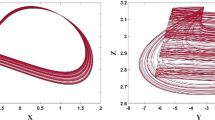
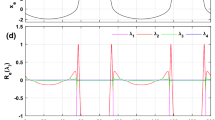
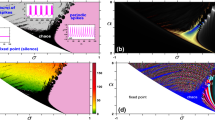
In this article we analytically solve the Hindmarsh–Rose model (Proc R Soc Lond B221:87–102, 1984) by means of a technique developed for strongly nonlinear problems—the step homotopy analysis method. This analytical algorithm, based on a modification of the standard homotopy analysis method, allows us to obtain a one-parameter family of explicit series solutions for the studied neuronal model. The Hindmarsh–Rose system represents a paradigmatic example of models developed to qualitatively reproduce the electrical activity of cell membranes. By using the homotopy solutions, we investigate the dynamical effect of two chosen biologically meaningful bifurcation parameters: the injected current I and the parameter r, representing the ratio of time scales between spiking (fast dynamics) and resting (slow dynamics). The auxiliary parameter involved in the analytical method provides us with an elegant way to ensure convergent series solutions of the neuronal model. Our analytical results are found to be in excellent agreement with the numerical simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Hindmarsh, J.L., Rose, R.M.: A model of neuronal bursting using three coupled 1st order differential equations. Proc. R. Soc. Lond. B221, 87–102 (1984)

    Article  Google Scholar 

  2. Hodgkin, A.L., Huxley, A.F.: A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544 (1952)

    Article  Google Scholar 

  3. Raninovich, M.I., Abarbanel, D.I., Huerta, R., Elson, R., Selverston, A.I.: Self-regularization of chaos in neural systems: experimental and theoretical results. IEEE Trans. CAS 44, 997–1005 (1997)

    Article  Google Scholar 

  4. Wand, W., Wang, Y., Wang, Z.D.: Firing and signal transduction associated with an intrinsic oscillation in neuronal systems. Phys. Rev. E 57, R2527 (1998)

    Article  Google Scholar 

  5. Baltanás, J.P., Casado, J.M.: Noise-induced resonances in the Hindmarsh–Rose neuronal model. Phys. Rev. E 65, 041915 (2002)

    Article  Google Scholar 

  6. Huerta, R., Bazhenov, M., Rabinovich, M.I.: Clusters of synchronization and bistability in lattices of chaotic neurons. Europhys. Lett. 43, 719–724 (1998)

    Article  Google Scholar 

  7. He, D.H., Zhan, M., Lu, H.P.: Periodic states with functional phase relation in weakly coupled chaotic Hindmarsh–Rose neurons. Phys. D 156, 314 (2001)

    Article  MATH  Google Scholar 

  8. Liao, S.J.: The proposed homotopy analysis techniques for the solution of nonlinear problems. Ph.D. Dissertation. Shanghai Jiao Tong University, Shanghai (1992)

  9. Liao, S.J.: Beyond Perturbation: Introduction to the Homotopy Analysis Method. CRC Press/Chapman and Hall, Boca Raton (2003)

    Book  Google Scholar 

  10. Liao, S.J., Tan, Y.: A general approach to obtain series solutions of nonlinear differential equations. Stud. Appl. Math. 119, 297–355 (2007)

    Article  MathSciNet  Google Scholar 

  11. Lyapunov, A. M.: General Problem on Stability of Motion (English translation). Taylor & Francis, London (1992) (The original one was published in 1892 in Russian)

  12. Adomian, A.: Nonlinear stochastic differential equations. J. Math. Anal. Appl. 55, 441–452 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  13. Adomian, A.: A review of the decomposition method and some recent results for nonlinear equations. Comput. Math. Appl. 21, 101–127 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  14. Adomian, A.: Solving Frontier Problems of Physics: The Decomposition Method. Kluwer Academic Publishers, Boston (1994)

    Book  MATH  Google Scholar 

  15. Liao, S.J.: An explicit, totally analytic approximation of Blasius’ viscous flow problems. Int. J. Nonlinear Mech. 34, 759–778 (1999)

  16. Liao, S.J.: On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 147, 499–513 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  17. Abbasbandy, S.: Solution for the FitzHugh–Nagumo equation with the homotopy analysis method. Appl. Math. Model. 32, 2706–2714 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  18. Bataineh, A.S., Noorani, M.S.M., Hashim, I.: Solving systems of ODEs by homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 13, 2060–2070 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  19. Mustafa, M., Khan, J.A., Hayat, T., Alsaedi, A.: Boundary layer flow of nanofluid over a nonlinearly stretching sheet with convective boundary condition. IEEE Trans. Nanotechnol. 14, 159–168 (2015)

    Article  Google Scholar 

  20. Mustafa, M., Khan, J.A., Hayat, T., Alsaedi, A.: Analytical and numerical solutions for axisymmetric flow of nanofluid due to non-linearly stretching sheet. Int. J. Non-Linear Mech. (2015). doi:10.1016/j.ijnonlinmec.2015.01.005

    Google Scholar 

  21. Khan, H., Mohapatra, R.N., Vajravelu, K., Liao, S.J.: The explicit series solution of SIR and SIS epidemic models. Appl. Math. Comput. 215, 653–669 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  22. Alomari, A.K., Noorani, M.S.M., Nazar, R., Li, C.P.: Homotopy analysis method for solving fractional Lorenz system. Commun. Nonlinear Sci. Numer. Simul. 15, 1864–1872 (2010)

    Article  MATH  Google Scholar 

  23. Corson, N., Aziz-Alaoui, M.A.: Asymptotic dynamics of the slow-fast Hindmarsh–Rose neuronal system. Dyn. Cont. Disc. Imp. Syst. Ser. B. Appl. Algorithms 16, 535 (2008)

    MathSciNet  Google Scholar 

  24. FitzHugh, R.: Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1, 445–466 (1961)

    Article  Google Scholar 

  25. Liao, S.: Advances in the Homotopy Analysis Method. World Scientific Publishing Co, Singapore (2014)

    Book  MATH  Google Scholar 

Download references

Acknowledgments

This work was partially funded by FCT/Portugal through the project PEst-OE/EEI/LA0009/2013. The authors would like to thank the anonymous reviewers of this article for all the helpful and constructive comments that have been made.

Author information

Authors and Affiliations

  1. Department of Mathematics, ISEL - Engineering Superior Institute of Lisbon, Rua Conselheiro Emídio Navarro 1, 1949-014, Lisbon, Portugal

    Jorge Duarte & Cristina Januário

  2. Mathematics Department, Center for Mathematical Analysis, Geometry and Dynamical Systems, Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais 1, 1049-001, Lisbon, Portugal

    Jorge Duarte & Nuno Martins

Authors
  1. Jorge Duarte
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Cristina Januário
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nuno Martins
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jorge Duarte.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Duarte, J., Januário, C. & Martins, N. On the analytical solutions of the Hindmarsh–Rose neuronal model. Nonlinear Dyn 82, 1221–1231 (2015). https://doi.org/10.1007/s11071-015-2228-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2228-5

Keywords

Search

Navigation