Abstract
The chaotic behavior of the secondary asteroid in a system of binary asteroids due to the asphericity and orbital eccentricity is investigated analytically and numerically. The binary asteroids are modeled with a sphere–ellipsoid model, in which the secondary asteroid is ellipsoid. The first-order resonance is studied for different values of asphericity and eccentricity of the secondary asteroid. The results of the Chirikov method are verified by Poincare section which show good agreement between analytical and numerical methods. It is also shown that asphericity and eccentricity affect the size of resonance regions such that beyond the threshold value, the resonance overlapping occurs and widespread chaos is visible.








Similar content being viewed by others
References
Bellerose, J., Scheeres, D.J.: Energy and stability in the full two body problem. Celest. Mech. Dyn. Astron. 100, 63–91 (2008)
Koon, W., Marsden, J.E., Ross, S.D., Lo, M., Scheeres, D.J.: Geometric mechanics and the dynamics of asteroid pairs. Ann. N. Y. Acad. Sci. 1017, 11–38 (2004)
Scheeres, D.J., Ostro, S.J., Werner, R.A., Asphaug, E., Hudson, R.S.: Effects of gravitational interactions on asteroid spin states. Icarus 147, 106–118 (2000)
Scheeres, D.J.: Bounds on rotation periods of disrupted binaries in the full 2-body problem. Celest. Mech. Dyn. Astron. 89(02), 127–140 (2004)
Fahnestock, E.G., Scheeres, D.J.: Simulation and analysis of the dynamics of binary near-Earth asteroid (66391) 1999 KW4. Icarus 194, 410–435 (2008)
Werner, R.A., Scheeres, D.J.: Mutual potential of homogeneous polyhedra. Celest. Mech. Dyn. Astron. 91, 337–349 (2005)
Cuk, M., Nesvorny, D.: Orbital evolution of small binary asteroids. Icarus 207, 732–743 (2010)
Steinberg, E., Sari, R.: Binary YORP and evolution of binary asteroids. Astron. J. 141(55), 1–10 (2011)
Zhao, Z., Chen, L.: Chemical chaos in enzyme kinetics. Nonlinear Dyn. 57(1–2), 135–142 (2009)
Farshidianfar, A., Saghafi, A.: Global bifurcation and chaos analysis in nonlinear vibration of spur gear systems. Nonlinear Dyn. 75(4), 783–806 (2014)
Jensen, C.N., True, H.: On a new route to chaos in railway dynamics. Nonlinear Dyn. 13(2), 117–129 (1997)
Gao, Q., Ma, J.: Chaos and Hopf bifurcation of a finance system. Nonlinear Dyn. 58(1–2), 209–216 (2009)
Hu, W., Zichen, D., Bo, W., Huajiang, O.: Chaos in an embedded single-walled carbon nanotube. Nonlinear Dyn. 72(1–2), 389–398 (2013)
Zounes, R.S., Rand, R.H.: Global behavior of a nonlinear quasiperiodic Mathieu equation. Nonlinear Dyn. 27(1), 87–105 (2002)
Abouhazim, N., Belhaq, M., Rand, R.H.: Two models for the parametric forcing of a nonlinear oscillator. Nonlinear Dyn. 50(1–2), 147–160 (2007)
Luo, A.C.: Resonance and stochastic layer in a parametrically excited pendulum. Nonlinear Dyn. 25(4), 355–367 (2001)
Murray, C.D., Dermott, S.F.: Solar System Dynamics. Cambridge University Press, Cambridge (1999)
Jose, J.V., Saletan, E.J.: Classical Dynamics: A Contemporary Approach. Cambridge University Press, Cambridge (1998)
Sussman, G.J., Wisdom, J., Mayer, M.E.: Structure and Interpretation of Classical Mechanics. MIT Press, Cambridge (2001)
Chirikov, B.V.: Universal instability of many-dimensional oscillator systems. Phys. Rep. 52(5), 263–379 (1979)
Lichtenberg, A.J., Lieberman, M.A.: Regular and Chaotic Dynamics, 2nd edn. Springer, Berlin (1992)
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
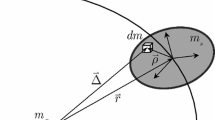
In this appendix, the potential energy for an ellipsoidal rigid body in gravitational field of point-mass body is derived. It is assumed that the ellipsoidal rigid body of the mass \(m_s \) is subjected to the gravitational attraction of a point-mass or homogenous spherical body with the mass \(m_p \). The distance between the two bodies is supposed to be large in comparison with the size of the ellipsoid body and also center of mass of the ellipsoid moves on a Keplerian orbit (see Fig. 9). The potential takes the form:

where \(G\) is the universal gravitational constant and  which
which  is instantaneous orbital radius vector and
is instantaneous orbital radius vector and  is the position vector of \(dm\) with respect to the center of mass of the ellipsoid.
is the position vector of \(dm\) with respect to the center of mass of the ellipsoid.
The magnitude of  can be expressed as
can be expressed as

By using these representation

the inverse of \(\varDelta \) is expanded by means of Legendre polynomials, \(P_l \) as followed
The first four Legendre polynomials are
which are utilized to derive approximate potential energy up to the third order, i.e.,
The first term is
This is well-known Newton’s law of universal gravitation.
Forasmuch as the origin coincides with the center of mass, as said before, the second term is:

It follows that \(V_2 \) is expressed as:

By using these useful expressions

where \(E\) is the unit matrix and \(I\) is the moment of inertia tensor, the \(V_2 \) is followed as

By introducing unit vector

and considering that the moment of inertia is calculated in the body coordinate
which \(T_B^\mathrm{ref} \) and \(T_\mathrm{ref}^B \) are transformation matrixes, transforming a vector from the body frame to the reference frame and vice versa, respectively, the final expression for \(V_2 \) is
There are some integrals of the form \(\int {x^{p}y^{q}z^{r}\,dm} \) in evaluating \(V_3 \). This integral for an ellipsoid which has three symmetry planes, is zero whenever one of \(p, q, r\) is odd. According to fourth term of Legendre polynomial, \(P_3 \) contains only odd powers. Therefore, \(V_3 \) vanishes.
Thus the potential energy up to the third order is
Since in this paper only the rotational motion of ellipsoid rigid body is considered, the term of potential energy which contributes on the rotational motion is
Appendix 2
In this appendix, the Eq. (9) is derived in details. Consider the second term of the Hamiltonian
The last part of this term can be written as
Also the \(\cos 2\!f\) and \(\sin 2\!f\) can be written in terms of sin and cos of the \(f\):
Using the series function based on the Bessel functions of the first kind, the following relations are used and substituted in the above equation :
Then
By simplifying above equation by elementary arithmetic and combining the terms and collecting all the coefficients with the same rational power of eccentricity up to third order of eccentricity, yields:
All of the above manipulations can be done using every computer algebra software such as Maple\({\copyright }\) and Mathematica\({\copyright }\).
Rights and permissions
About this article
Cite this article
Jafari Nadoushan, M., Assadian, N. Widespread chaos in rotation of the secondary asteroid in a binary system. Nonlinear Dyn 81, 2031–2042 (2015). https://doi.org/10.1007/s11071-015-2123-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-015-2123-0