1 Introduction

It is well known that chaotic dynamics is not restricted only to complicated and strongly nonlinear vector fields [1] but can be observed also in the case of algebraically simple systems with six terms including nonlinearity [2]. Recent progress in overall performance of the personal computers and possibility of multi-grid calculation allows to implement fast-to-be-calculated quantifier of the dynamical motion inside a procedure for chaos or hyper-chaos localization [3]. Doing this we can start searching for irregular behavior of arbitrary-order nonlinear dynamical system. Such process begins with analytical definition of dimensionless mathematical models and continues with specification of the internal system parameters which are so far unknown. Since coexistence of multiple different attractors is possible in such systems, the initial conditions are randomly and, more importantly, repeatedly chosen. Each time a routine comes across vector field which provides the so-called folding and stretching mechanism, the dynamical system is remembered for consequent numerical analysis.

This work has been primarily motivated by two recently published research papers where a group of dynamical systems with very specific properties have been presented. In paper [4] a class of the dynamical systems without equilibrium has been presented. Similarly paper [5] introduces several dynamical systems with a line equilibrium. Both works can be considered as a breakthrough idea since chaos is often put into the context of the singular saddle-type fixed points; the most common configuration of the vector field contains two [6] or three[7] of them. From this point of view a system with circular equilibrium (CES) represents somehow future logical progress.

2 Mathematical models under inspection

As previously mentioned first step toward discovery of new chaotic dynamics goes through a choice of dimensionless set of three first-order differential equations

$$\begin{aligned} \frac{{\text {d}}x}{{\text {d}}t}= & {} a\cdot z \nonumber \\ \frac{{\text {d}}y}{{\text {d}}t}= & {} z \cdot f_{1}(x,y,z) \nonumber \\ \frac{{\text {d}}z}{{\text {d}}t}= & {} x^2+y^2 - r^2 +z \cdot f_{2}(x,y,z), \end{aligned}$$
(1)

where \(r\) became radius of circular equilibrium and \(a\) marks free parameter. Of course a predefined form (1) is not unique for CES; it is only the most straightforward realization of system containing fixed points which form a circle located on the plane \(z=0\). The nonlinear functions \(f_1\) and \(f_2\) can contain a variety of terms; eventually it seems that several quadratic polynomials are sufficient to generate necessary geometrical structure of a vector field. In particular search routine reveals following smooth functions

$$\begin{aligned} f_{1}(x,y,z)= & {} b \cdot x+c \cdot z^2 \nonumber \\ f_{2}(x,y,z)= & {} d \cdot x, \end{aligned}$$
(2)

where \(b\), \(c\) and \(d\) are remaining free constants. The numerical values of all free parameters are following

$$\begin{aligned} a=-0.1 \quad b=3 \quad c=-2.2 \quad d=-0.1 \quad r=1, \end{aligned}$$
(3)

for which a chaotic attractor evolves. To prove it Mathcad and built-in fourth-order Runge–Kutta integration method have been employed with final time \(5000\) and time step equals to \(0.1\) as demonstrated by means of Fig. 1.

Fig. 1
figure 1

3D perspective view of the chaotic attractor without initial transient motion and associated plane projections for a \(d = -0.15\), b \(d = -0.12\), c \(d = -0.10\) with equilibrium half-circle located in plane \(z = 0\)

Full size image

The initial conditions can be taken as \(\mathbf x _0=(0, 0, 0)^T\). Typical property of this dynamical system is long spiral-type transient behavior and dissipative dynamical flow given by parameter \(d\).

Figure 2 demonstrates the regions of chaotic solution in the hyper-space of the internal system parameters where a concept of the largest Lyapunov exponent (LE) is adopted. The LEs are calculated using Jacobi matrix (4) as presented in [8]. In order to get better insight into global dynamics only fragments of this hyper-space are demonstrated. The dark blue color in the topographically scaled graphs should be understood as limit cycle and green as a weakly chaotic system, and yellow denotes chaotic motion. Discovered dynamical system possesses several attractors; see the basins of attraction provided in Fig. 3.

Fig. 2
figure 2

A contour-surface plots of the largest Lyapunov exponent (LE) for two variable parameters while remaining two are fixed at default values (3). The positive value of LE stands for chaotic solution

Full size image
Fig. 3
figure 3

Cross sections of basin of attraction, from left to right \(z=-1\), \(z=-0.5\), \(z=0\), \(z=0.5\), \(z=1\) (white color represent unbounded solutions, black areas are fixed points, and gray regions denote chaotic motion)

Full size image

Dynamical motion in the close neighborhood of the equilibrium circle is determined by the eigenvalues and associated eigenspaces established along this structure [9]. In the case of (1) and (2) a state-dependent linearization matrix can be established as

$$\begin{aligned} \mathbf J(x) =\left( \begin{array}{ccc} 0 &{} 0 &{} a \\ b\cdot z &{} 0 &{} b \cdot x+3\cdot c \cdot z^2 \\ 2 \cdot x + d\cdot z &{} 2\cdot y &{} d \cdot x \end{array}\right) \end{aligned}$$
(4)

A local behavior along the equilibrium circle is determined by the so-called eigenvalues, i.e., roots of the parameterized characteristic equation

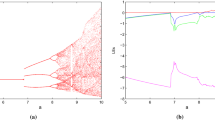
$$\begin{aligned} \lambda (x)= & {} \lambda ^3-d \cdot x \cdot \lambda ^2 \\&- 2 \cdot x \cdot \left( a \pm b \sqrt{r^2-x^2}\right) \cdot \lambda =0. \nonumber \end{aligned}$$
(5)

One eigenvalue is zero, and the remaining two depend on a position on the equilibrium circle. Obviously there always exists a center manifold, and dynamical motion in the neighborhood of this circle can be decomposed into different configurations of the remaining two-dimensional subspace. Its nature can be clarified by means of Fig. 4.

Fig. 4
figure 4

A local behavior of the discovered system: a two remaining eigenvalues and the associated two-dimensional subspace: red (saddle-type), blue (stable spiral), green (unstable spiral), b dynamical motion with initial conditions near equilibrium circle (outside) and c dynamical motion with initial conditions near equilibrium circle (inside)

Full size image

After huge efforts it turns out that even simpler system without nonlinear function \(f_2\) can get very close to the situation where it exhibits chaotic motion, in detail

$$\begin{aligned} \frac{{\text {d}}x}{{\text {d}}t}= & {} z \nonumber \\ \frac{{\text {d}}y}{{\text {d}}t}= & {} z \cdot f(x,y,z) \nonumber \\ \frac{{\text {d}}z}{{\text {d}}t}= & {} x^2+y^2-r^2, \end{aligned}$$
(6)

and this expression can be marked as canonical polynomial CES.

3 Experimental verification

To illustrate that dynamical systems (1) and (2) provide chaotic attractor with certain degree of the structural stability it has been implemented as a lumped electronic circuit. For network synthesis we choose a concept based on integrator block schematic [10, 11]. Final network is given in Fig. 5 where route-to-chaos scenario can be traced via a change in the external dc voltage supply \(Vd\). Since desired chaotic attractor is bounded into relatively small state space volume, the dynamical ranges of used active devices can be also reduced. Thus a four-channel four-quadrant analog multiplier MLT04 has been chosen for implementation of the quadratic terms. The supply voltage for these devices is symmetrical \(\pm 5\) V. Voltage limitation of this active device occurs for values outside of \(\pm 2.5\) V range. Thus strange attractors that occupy bigger volumes in the state space cannot be realized by the proposed circuitry. For mathematical operations integration and summation a basic inverting voltage-mode two ports with voltage feedback operational amplifier TL084 are utilized. In this case a supply voltage is raised to symmetrical \(\pm 15\) V. The time constant of the ideal integrators is chosen to be only \(\tau =RC=10^{-4}s\) such that parasitic properties of the utilized active elements can be neglected. The individual state variables are easily measurable at the output nodes of the lossless integrators. Sixth multiplier is used in order to control bifurcation parameter \(d\) via external dc voltage source and can be removed for further network simplification.

Fig. 5
figure 5

Circuitry realization of CES

Full size image

If active devices can be considered as close enough to ideal and by assumption of a fundamental transformation of the coordinates \((-x, y, -z) \rightarrow (u_1, u_2, u_3)\), the describing differential equations became

$$\begin{aligned} \frac{{\text {d}} u_1}{{\text {d}}t}= & {} -\frac{u_3}{R_1 C} \nonumber \\ \frac{{\text {d}} u_2}{{\text {d}}t}= & {} \frac{u_3}{R_6 K_3 C}\left( \frac{R_2}{R_3}u_1 + \frac{R_2}{R_5 K_1} u_3^2\right) , \nonumber \\ \frac{{\text {d}} u_3}{{\text {d}}t}= & {} \frac{1}{C} \left( \frac{u_1^2}{R_7 K_2} + \frac{u_2^2 }{R_8 K_4} - \frac{V_{r}}{R_9}-\frac{u_1 u_3 V_d}{R_4 K_5 K_6} \right) \end{aligned}$$
(7)

where \(K_i=5/2\) is internally trimmed scaling factor of \(i\)-th multiplier. The set of values for circuit realization can be calculated by a comparison of the individual terms of (7) with system (1) having functions (2) with numerical values (3), in detail

$$\begin{aligned} \begin{array}{ll} V_r=r^2=1 V &{} V_d=-d \\ R_1=\frac{-R}{a}=10{\text {k}}\Omega &{} R_2=R_9=R=1\,{\text {k}}\Omega \\ R_3=\frac{R}{b}=333 \Omega &{} R_4=\frac{R}{K_5 K_6}=160\,\Omega \\ R_5=\frac{-R}{K_1 c}=182 \Omega &{} R_6=\frac{R}{K_3}=400\,\Omega \\ R_7=\frac{R}{K_2}=400 \Omega &{} R_8=\frac{R}{K_4}=400\,\Omega . \end{array} \end{aligned}$$
(8)

If natural frequency components of the chaotic waveforms need to be moved behind 1 MHz, the non-ideal and parasitic properties of the used active elements need to be analyzed. Unlike others especially input and output admittances in the form of a parallel combination of resistor and capacitor as well as roll-off nature of a transfer function typical for both MLT04 and TL084 should be respected. These unwanted features can introduce several error terms into describing differential equations causing deformation of the desired chaotic attractor or its geometrical collapse. Note that only three integrated circuits are required for design of the proposed chaotic oscillator. The circuit was evaluated by circuit simulator Orcad Pspice, and the voltage spectrum and plane projections can be seen in Fig. 6.

Fig. 6
figure 6

Time-domain analysis of designed chaotic oscillator by using Orcad Pspice circuit simulator: a power spectra of \(u_1\) and \(u_2\) signals, b \(xy\) (blue) and \(xz\) (red) plane projections

Full size image

The circuit was designed on breadboard, and in experimental setup digital oscilloscope HP54603B was used for attractor visualization, see Fig. 7. Based on the computed riddled basins of attraction serious problems have to be expected during measurement. Before documentation of each particular routing-to-chaos scenario predefined initial conditions need to be imposed into the oscillator. However, this additional circuitry is not provided.

Fig. 7
figure 7

Oscilloscope traces of the chaotic attractors. Projection of the chaos evolution onto (upper left:\(xy\), upper right: \(xz\), bottom: \(yz\)) plane: a Vd = 800 mV, b Vd = 500 mV, c Vd = 480 mV, d Vd = 420 mV, e Vd = 400 mV, f Vd = 250 mV

Full size image

4 Conclusion

In this short paper a novel dynamical system with circular equilibrium is uncovered and numerically confirmed as well as experimentally measured. Brief nature of this paper leaves the place for upcoming deeper investigation of the class of dynamical system with circular equilibrium. It is believed that brute-force method that combines stochastic search routine with objective function in the form of precise motion quantifier is powerful tool which can be utilized for discovering interesting dynamical systems with prescribed features. As indicated by new publications [6, 12] research in this particular area will proceed in the near future.