Understanding memristors and memcapacitors in engineering mechanics applications

Abstract

A significant event happened for electrical engineering in 2008, when researchers at HP Labs announced that they had found “the missing memristor,” a fourth basic circuit element that was postulated nearly four decades earlier by Dr. Leon Chua, who was also instrumental in developing the mathematical theories of memristive, memcapacitive, and meminductive systems, resulting in an entire class of “mem-models” that are the foundation of the present work. By applying well-known mechanical–electrical analogies, the mathematics of mem-models may be transferred to the setting of engineering mechanics, creating the mechanical counterparts of memristors, memcapacitors, etc. However, this transfer is nontrivial; for example, a new concept and state variable called “absement,” the time integral of deformation, emerge. We study these mem-models, which are characterized by a “zero-crossing” property that has interesting implications for nonlinear constitutive modeling, particularly hysteresis, and we identify some examples of “mem-dashpots” and “mem-springs,” which include displacement-dependent and variable dampers, the superelasticity found in shape-memory alloys, and the pinched hysteresis loops associated with self-centering structures. This work adds to the fast-growing body of literature on elements and systems labeled with “mem,” which is a basic branch of study in nonlinear dynamics.

Appendices

Appendix 1 for Sect. 2

Table 7 lists various definitions of the memristor and the publications from which they were taken. First, these seemingly different definitions are indeed all consistent once notational differences are taken into account. Next, they are for either a general or a specific electrical system. Last, they distinguish a flow-controlled electrical device from an effort-controlled electrical device. For electrical systems, charge- or current-controlled are aliases for flow-controlled, while flux-, voltage-, or impulse-controlled are aliases for effort-controlled.

Table 7 Many faces of mathematical expressions for the memristor

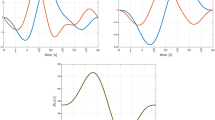
Figure 25 depicts some simple situations where the necessity to contrast flow- and effort-controlled mechanical systems becomes evident. After all, basic elements like springs, dampers, or memristors are made to be used repetitively and in a well-organized manner in order to form a “system” that models a complex real-world device or structure. For translational mechanics, the connectivity of these basic elements can be reduced to either parallel or serial connections, the roots of the concepts of flow- and effort-controlled systems.

Fig. 25

1a A Kelvin model connected in series with a mass, 1b a Maxwell model connected in series with a mass, 2a a Kelvin model connected with a memristor in parallel and then connected in series with a mass, 2b a Maxwell model connected with a memristor in series and then connected in series with a mass. Each is subject to a prescribed force $u(t)$

Figure 251a and 1b shows the Kelvin and Maxwell models, each connected in series with a mass. Jeltsema and Scherpen [24] reveal the duality between these flow- and effort-controlled systems, expressed in terms of integro-differential equations. In a flow-controlled device, the natural state variables are displacement $x$ and velocity $\dot{x}$. These state variables should be solved (or calculated) first by integrating the differential equation based on force equilibrium. In contrast, in an effort-controlled device, the natural state variables are momentum $p$ and restoring force $r$, where momentum is the time integral of restoring force. These state variables should be solved (or calculated) first from the equation based on deformation compatibility.

These two linear time-invariant flow- and effort-controlled systems may be extended by introducing a new element—such as the memristor (nonlinear time-invariant)—as shown in Fig. 25 2a and 2b. Table 8 presents the state variables and state equations for the corresponding models in Fig. 25, where $u(t)$ is an applied force as in Eq. (1). For systems in general, the constitutive relations of all components—either elements or systems—need to be “assembled” in accord with the connectivity of the components. In the absence of other important details, the need for two different mathematical expressions for the same memristor to fit into these two different systems may be seen clearly. In other words, when doing computations, we may need to deal with either a flow-controlled memristor or an effort-controlled memristor, depending on the element or system connectivity.

Table 8 Summary of possible state variables and equations for all cases in Fig. 25

Table 9 lists expressions that are analogous to the set of ($v$, $i$) plots in Strukov [42] under the title of “Curious Lay Person’s Viewgraph—II,” plus one more for the memcapacitor. Table 9 also illustrates the underlying mathematical parallelism in the case of sinusoidal excitation.

Table 9 Periodic solution for spring and memcapacitor subject to $^\dag x(t) = A \sin \left( \omega t \right)$, and for mass, dashpot, and memristor subject to $^\ddag \dot{x}(t) = A \sin \left( \omega t \right)$

The proof to Remark 4 is given below. The equation of motion corresponding to Fig. 25(2a) is:

$$\begin{aligned}&m \ddot{x} + k x = u - \left[ c + M(x) \right] \dot{x},~\text {with}~x(0) = x_0,\nonumber \\&\dot{x}(0) = \dot{x}_0 \end{aligned}$$

(43)

Assume free vibration; i.e., $u = 0$. Multiply both sides of Eq. (43) by $\dot{x}(t)$. Note that

$$\begin{aligned} \left( m \ddot{x} + k x \right) \dot{x} = \frac{\mathrm{d}}{\mathrm{d}t} E(t) \end{aligned}$$

(44)

where $E(t) = \frac{1}{2} m \dot{x}^2 + \frac{1}{2} k x^2$. Multiply this equation by $dt$ and integrate from $t = 0$ to $t = T$ to obtain $E(T) = E(0) - \varDelta (T)$, where

$$\begin{aligned} \varDelta (T) = \int _0^T \left[ c + M(x) \right] \dot{x}^2 dt \end{aligned}$$

(45)

is a dissipation function. If $c + M(x) \ge 0$, $\forall x(t)$, then $\varDelta (T) \ge 0$. Thus, $M(x) \ge -c$ is sufficient for passivity (i.e., no produced energy).

Appendix 2 for Sect. 3

Examples of mem-dashpots are given in Table 10. See Tables 11 and 12 for some models used in Sects. 3.3 and 3.4, respectively. Table 13 and Figs. 26 and 27 are also referred to in Sect. 3.

Table 10 Examples of mem-dashpots

Table 11 Secant stiffness $S(a)$ used in simple mem-spring models $r = S(a)x$ in Sect. 3.3

Table 12 Secant stiffness $S(a, x)$ used in simple mem-spring models $r = S(a, x) x$ in Sect. 3.4

Table 13 Values and $S$, $K$, and $U$ at the controlling points within a cycle for selected models given in Sect. 3.4

Appendix 3 for Sect. 4

1.1 Case studies from nano-field

Tables 14 and 15 give an overview of all these case studies.

Table 14 Three case studies on nano-devices selected as case studies herein with the equation or page numbers appeared in these papers

Table 15 Case studies: Both the state and input–output equations are from the original papers where they are cited from

1.2 Understanding case study #3

To see that $W = \frac{i(t)}{v(t)}$ is a bivariate function of $v(t)$ and $\phi (t)$, note that $i(t)$, defined by Eq. (58), is a bivariate function of $w(t)$ and $v(t)$. Applying the fundamental existence-uniqueness theorem for ODEs (e.g., in [18]) to Eq. (57), the solution exists and is unique on an open set for $v$; i.e., ($w$, $\phi$) is one-to-one (since the hyperbolic sine in Eq. (57) is analytic and thus satisfies the Lipschitz condition). Hence, $W = f( w(\phi ), v) = g( \phi , v)$.

Hereafter, consider only prescribed piecewise linear $v(t)$ as in [7]. Assume $v(t) = bt + c$ for a generic section of the excitation and proceed as follows:

$$\begin{aligned} \frac{\mathrm{d}\phi }{\mathrm{d}v} = \frac{\dot{\phi }}{\dot{v}} = \frac{v(t)}{b} \end{aligned}$$

(59)

leading to the following piecewise relation for the phase plot ($\phi$, $v$):

$$\begin{aligned} \phi (t) = \frac{v^2(t)}{2b} + \phi _0 \Longrightarrow v(t) = \pm \sqrt{2b(\phi (t) - \phi _0)}\nonumber \\ \end{aligned}$$

(60)

The general solution to Eq. (57) with $v(t) = bt + c$ is:

$$\begin{aligned}&w(t) = w(t_0) + \frac{2 \lambda }{\eta b} \left[ \cosh (\eta v(t)) - \cosh (\eta bt_0 + \eta c) \right] \end{aligned}$$

(61)

$$\begin{aligned}&\mathop {=}\limits ^{\text {Eq. (60)}} w(t_0)+ \frac{2 \lambda }{\eta b} \left[ \cosh \left( \pm \eta \sqrt{2b \left( \phi (t) - \phi _0 \right) } \right) \right. \nonumber \\&\quad -\, \left. \cosh (\eta bt_0 + \eta c) \right] \end{aligned}$$

(62)

where the sign $\pm$ remains the same within each piece as before. Clearly, ($w$, $\phi$) is a one-to-one mapping within each piece of the solution curve separated by the time events. Given that $\cosh$ is an even function, the first and third quadrants in ($v$, $i$) share the same ($w$, $\phi$). These can be verified in Fig. 28.

Fig. 26

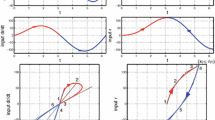
Two system models (see Table 12) illustrate the behavior of ($x$, $r$) at $x = 0$ and the impact of a Situation (1) and b Situation (2) to the tangent stiffness of ($x$, $r$); $x(t) = A \sin (\omega t)$ with $A = 1$ and $\omega = 1$

Fig. 27

Same system models as in Fig. 26 (see Table 12) but subject to $x(t) = \frac{4A}{T} \left( t - \frac{T}{2} \left\lfloor \frac{2t}{T} + \frac{1}{2} \right\rfloor \right) (-1)^{\lfloor \frac{2t}{T} + \frac{1}{2} \rfloor },\hbox {with}\, a(0) = 0,~T = \frac{2\pi }{\omega }$, $A = 1$, and $\omega = 1$. This is to illustrate the behavior of ($x$, $r$) at $x = 0$ and the impact of a Situation (1), and b Situation (2) to the tangent stiffness of ($x$, $r$)

Fig. 28

More insights in terms of $\frac{w}{D}$ to understand Chang et al.’s  [7] Fig. 5a and Fig. 5b

Substituting Eqs. (58) to (61), it can be seen that, for a pair of $v$ and $-v$, the absolute values of their $i$ differ, so do their $q$ and $W$ values—as stated in the caption for Fig. 19. Indeed, this system is not a memristor; rather, it is a memristive system.

In fact, the pair of $\dot{w}$ and $v$ defined in Eq. (57) represents a relationship in a nonlinear resister with $\dot{w}$ and $w$ corresponding to current and charge, respectively. Having said this, ($w$, $\phi$) must be a one-to-one mapping as stated above and illustrated in Fig. 28. Alternatively (and at the risk of unnecessary length), the one-to-one’ness and inflection points on ($w$, $\phi$) shown in Fig. 28 can be understood as follows:

$$\begin{aligned} \frac{\mathrm{d}w}{\mathrm{d}\phi } = \frac{\dot{w}}{\dot{\phi }} = \frac{2 \lambda \sinh (\eta v)}{v} \end{aligned}$$

(63)

For all $v(t)$, $\frac{\mathrm{d}w}{\mathrm{d}\phi } > 0$, which explains the monotonic ($w$, $\phi$); i.e., ($w$, $\phi$) is one-to-one for all $t$. Furthermore, the continuity of $\sinh$ can be used to explain the continuity of ($w$, $\phi$) even when $v(t)$ is only ${\mathcal {C}}^0$ continuous.

Appendix 4 for Sect. 5

A prototype mem-spring model for SMA wire is given herein. While the models in Figs. 26 and 27 could be candidates for SMA wire in tension (e,g., those in [14]), there is a useful methodology for establishing a memcapacitor model for any individual set of SMA wire data under a clearly defined excitation—if we adopt the philosophy of Sect. 4.6 by paying attention to time-varying secants. For the piecewise-defined displacement in Eqs. (13) to (16), this methodology is illustrated in Fig. 29 and explained hereafter.

Fig. 29

Illustrations of the procedure of developing a memcapacitor model by using an arbitrary set of SMA wire under a piecewise linear displacement as in Eqs. (13) to (16)

Fig. 30

To expand on Fig. 9, different variations in the hysteric loop in the first quadrant (subject to a piecewise linear displacement) and their corresponding models. The piecewise linear displacement is defined in Eqs. (13) to (16) with $a(0) = 0$, $A = 1$, and $\omega = 1$. Five sets of values are used for $x_1$, $r_1$, and $x_2$

The mathematical expressions involved in modeling—for the example illustrated in Fig. 29—are given as follows:

$$\begin{aligned} r_1 \left( x \right)&\Rightarrow s_1 \left( x \right) = \frac{r_1 \left( x \right) }{x} = s_1 \left( h_1(a) \right) = S_1 (a)\end{aligned}$$

(64)

$$\begin{aligned} r_2 \left( x \right)&\Rightarrow s_2 \left( x \right) = \frac{r_2 \left( x \right) }{x} = s_2 \left( h_2(a) \right) = S_2 (a) \end{aligned}$$

(65)

To clearly demonstrate this modeling method, Fig. 9 presented previously is utilized again. The restoring force versus displacement plot in the first quadrant is examined first. As shown in Fig. 30, the model parameters $x_1$, $r_1$, and $x_2$ are to be given in advance. Others can be conveniently obtained from geometry: $r_2 = R - \frac{A - x_2}{x_1} r_1$ and where $R$ is the restoring force corresponding to A, and $x_3 = x_2 - (A - x_1)$; $r_3 = \frac{x_3}{x_1} r_1$. The corresponding absement values are: $a_1 = \frac{T}{8A} x_1^2$; $a_2 = 2 a_0 - \frac{T}{8A} x_2^2$, and $a_3 = 2 a_0 - \frac{T}{8A} x_3^2$. By varying the values of $x_1$, $r_1$ and $x_2$, a set of these sub-models are obtained. In all these sub-models, applying Eqs. (64) and (65) but considering a total of five pieces that characterize an experimental restoring force versus displacement plot, we have the following equations to define $S(a)$ in a piecewise manner:

(66)

(67)

(68)

(69)

(70)

After finishing modeling the first quadrant, the model in the third quadrant must be made “anti-symmetric with respect to the origin” following [13] (see Sect. 3.4), which is conveniently carried out, say, using vector concatenation under MATLAB$^\mathrm{TM}$. Mathematically, this could be done using either of two approaches given in Sects. 5.2 and 5.3. Data sets from other analytic or piecewise continuous displacements can be treated in a similar manner.