A wavelet-based approach for stability analysis of periodic delay-differential systems with discrete delay

Abstract

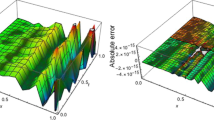
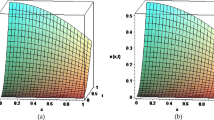
This paper presents a semi-analytical wavelet-based approach for stability analysis of time-periodic delay-differential equations (DDEs) with a single discrete time delay. By using the autocorrelation functions of compactly supported Daubechies scaling functions, the DDE is discretized to a set of algebraic equations, employing the wavelet collocation method. The state transition matrix over a single period is constructed to determine the stability based on Floquet theory. Stability charts for the one-degree-of-freedom milling model and time-delayed Mathieu equation are obtained, illustrating both the efficiency and accuracy of the proposed approach.

Appendices

Appendix A: Multiresolution analysis and Daubechies scaling function [40]

A multiresolution analysis is a sequence $\{V_J\}, J\in {\mathbb {Z}}$ of subspaces of $L^{2}(\mathbb {R})$ with the following properties:

$$\begin{aligned}&V_J \subset V_{J+1},\quad \forall J\in \mathbb {Z} \end{aligned}$$

(31)

$$\begin{aligned}&\overline{\bigcup _{J\in {\mathbb {Z}}} {V_J}} =L^{2}({\mathbb {R}}), \quad \hbox {and}\quad \bigcap _{J\in {\mathbb {Z}}} {V_J} =\{0\}\end{aligned}$$

(32)

$$\begin{aligned}&f(x)\in V_J \Leftrightarrow f(2x)\in V_{J+1},\quad \forall J\in {\mathbb {Z}} \end{aligned}$$

(33)

$$\begin{aligned}&f(x)\in V_J \Leftrightarrow f(x-2^{-J}k)\in V_J,\quad \forall k\in \mathbb {Z} \end{aligned}$$

(34)

The Daubechies scaling function, ${\varphi } (t)$, with $M$ vanishing moments, is constructed by applying the iterative procedure [40]

$$\begin{aligned} {\varphi } (t)=\sqrt{2}\sum _{k=0}^{2M-1} {h_k {\varphi } (2t-k)} \end{aligned}$$

(35)

where $h_k$ are the Daubechies filter coefficients (Table 2). The set $\{ {\phi (t-k),k\in {\mathbb {Z}}}\}$ is an orthonormal basis for $V_0$. The support of the scaling function ${\varphi } (t)$ is $[0,L]$, and $L=2M-1$, where the support of ${\varphi } (t)$ means an interval $P$ such that ${\varphi } (t)=0$, for $t \notin P$.

The corresponding Daubechies wavelet function $\psi (t)$ can be expressed as

$$\begin{aligned} \psi (t)=\sqrt{2}\sum _{k=0}^{2M-1} {(-1)^{k+1}h_k {\varphi } (2t+k-1)} \end{aligned}$$

(36)

The Daubechies wavelet function has the following property, i.e.,

$$\begin{aligned} \int _{-\infty }^{+\infty } {t^{k}\psi (t)\hbox {d}t}=0,\quad \hbox {for}\; k=0,\ldots ,M-1 \end{aligned}$$

(37)

where it means $\psi (t)$ has its first $M$ moments vanish.

Table 2 Coefficients $h_k$ for Daubechies scaling function with $M$ vanishing moments [40]

Appendix B: Formulation of the single DOF milling system

The governing equation of the single DOF milling system can be formulated as [9]

$$\begin{aligned} {\ddot{x}}(t)+2\zeta \omega _n \dot{x}(t)+\omega _\mathrm{n}^2 x(t){=}-\frac{a_p h(t)}{m_t }({x(t){-}x(t-T)}) \end{aligned}$$

(38)

where $\zeta$ is the relative damping, $\omega _\mathrm{n}$ is the angular natural frequency, $m_t$ is the modal mass of the cutter, $a_p$ is the depth of cut, and $h(t)$ is the cutting force coefficient.

By denoting that $y(t)=m_t\frac{\hbox {d}}{\hbox {d}t}x(t)+m_t \zeta \omega _n x(t)$ and ${\mathbf{x}}(t)=[x(t) \quad y(t)]^\mathrm{T}$, Eq. (38) can be represented as the state-space form, i.e.,

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}{\mathbf{x}}(t)=\mathbf{A}(t)\mathbf{x}(t)+\mathbf{B}(t)\mathbf{x}(t-T) \end{aligned}$$

(39)

where

$$\begin{aligned} \mathbf{A}(t)&= \left[ {{\begin{array}{ll} -\zeta \omega _n &{} \frac{1}{m_t} \\ {m_t \left( {\zeta \omega _n } \right) ^{2}-m_t \omega _n^2 -a_p h(t)}&{} {-\zeta \omega _n} \\ \end{array} }} \right] , \nonumber \\ \mathbf{B}(t)&= \left[ {{\begin{array}{ll} 0 &{} 0 \\ a_p h(t) &{} 0 \\ \end{array}}} \right] \end{aligned}$$

(40)