Abstract
The nonlinear flutter oscillations of a restrained cantilevered plate induced by subsonic flow have been investigated in this paper. A non-smooth piecewise linear spring is considered to simulate the motion constraints. A set of discrete equations is obtained by the Galerkin method. Emphasis is placed on the limit cycle oscillations (LCOs) of the aeroelastic system due to the nonlinearity. A flutter determinant is developed to the analysis of flutter instability. The system loses stability by flutter and undergoes LCOs afterward due to the nonlinearity. The stability of LCOs is addressed on the basis of the equivalent linearized method. The location of the nonlinear motion constraints is intimately bound up with the type of Hopf bifurcations (subcritical or supercritical). Interestingly, for some special cases, the Hopf bifurcations are both subcritical and supercritical. The two-multiple semi-stable limit cycle bifurcation due to the extreme point of the flutter curve is also determined. The analytical results predicted by the analysis scheme are sufficiently validated by numerical calculations.





















Similar content being viewed by others
Abbreviations
- \(c_{ij}\) :
-
The element of damping matrix \(\mathbf{C}\)
- \(D\) :
-
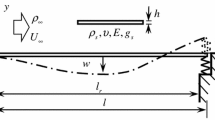
Plate bending stiffness \(=\,{Eh^{3}}/{[12(1-\upsilon ^{2})]}\)
- \(E\) :
-
Plate elastic modulus
- \(f_{\mathrm{non}}\) :
-
Force of nonlinear spring support
- \(g_\mathrm{s}\) :
-
Structural damping coefficient of plate
- \(h\) :
-
Plate thickness
- \(K_1, K_2\) :
-
Linear stiffness of nonlinear spring support
- \(k_{ij}\) :
-
The element of stiffness matrix \(\mathbf{K}\)
- \(k_{\mathrm{eq}}\) :
-
Equivalent linearization stiffness
- \(l\) :
-
Plate length
- \(l_r\) :
-
Location of motion constraints
- \((\mathrm{LCO})_\mathrm{s}\) :
-
A stable LCO
- \((\mathrm{LCO})_\mathrm{u}\) :
-
An unstable LCO
- \(m_{ij}\) :
-
The element of mass matrix \(\mathbf{M}\)
- \(n\) :
-
Mode number
- \(N\) :
-
Total number of modes
- \(q_n\) :
-
\(n\)th mode amplitude
- \(s_n\) :
-
\(n\)th eigenvalue of a cantilever beam: \(s_1=1.875,s_2 =4.694\)
- \(k_{ij}\) :
-
The element of matrix \(\mathbf{K}\)
- \(\mathbf{O}_A^{\mathrm{s(u)}}\) :
-
Stable (unstable) fixed point \(\mathbf{O}_A\)
- \(P_\mathrm{s}\) :
-
Amplitude of a stable LCO
- \(\Delta P_\mathrm{s}\) :
-
Increment of amplitude of a stable LCO
- \((p_1)_0\) :
-
Initial condition of \(p_1 \)
- \(t\) :
-
Time
- \(u_\infty \) :
-
Velocity of air at freestream
- \(w\) :
-
Plate bending deflection
- \(w_0\) :
-
Initial deviation of the nonlinear spring
- \(\mathbf{X}\) :
-
State space
- \(x\) :
-
Stream-wise spatial coordinate
- \(y\) :
-
Coordinate normal to plane of plate
- \(\delta (\cdot )\) :
-
Dirac-delta function
- \(\omega _\mathrm{f}\) :
-
Flutter frequency
- \(\varphi _n\) :
-
\(n\)th eigenfunction of a cantilevered beam
- \(\upsilon \) :
-
Poisson’s ratio
- \(\rho _\mathrm{s}\) :
-
Plate density
- \(\rho _\infty \) :
-
Density of air at freestream
- \(\lambda _\mathrm{f}\) :
-
Flutter critical dynamic pressure
- \(\lambda _A\) :
-
Flutter critical dynamic pressure corresponding to the fixed point \(\mathbf{O}_A \)
- \(\lambda _B\) :
-
Flutter critical dynamic pressure corresponding to the fixed point \(\mathbf{O}_B \)
- \(\lambda _C\) :
-
Flutter critical dynamic pressure corresponding to the maximum \(k_\mathrm{eq} \)
- \(\lambda _h\) :
-
Flutter critical dynamic pressure corresponding to \(k_\mathrm{eq}\)
- \(\lambda _{M}\) :
-
Critical dynamic pressure of the two-multiple semi-stable cycle bifurcation
- \(\lambda _t\) :
-
Dynamic pressure for a LCO
References
Jeromr, C.R.: A train for the 21st century. Rail Int. 25, 2–8 (1994)
Raghunathan, R.S., Kim, H.D., Setoguchi, T.: Aerodynamics of high-speed railway trains. Prog. Aerosp. Sci. 38, 469–514 (2002)
Li, P., Yang, Y.R., Zhang, M.L.: Melnikov’s method for chaos of a two-dimensional thin panel in subsonic flow with external excitation. Mech. Res. Commun. 38, 524–528 (2011)
Dowell, E.H.: Aeroelasticity of Plates and Shells. Noordhoff International Publishing, Leyden (1975)
Païdoussis, M.P.: Fluid-Structure Interactions. Slender Structures and Axial Flow, vol. 2, 1st edn. Elsevier Academic Press, London (2004)
Dugundji, J., Dowell, E.H., Perkin, B.: Subsonic flutter of panels on continuous elastic foundations. AIAA J. 5, 1146–1154 (1963)
Kornecki, A., Dowell, E.H., O’Brien, J.: On the aeroelastic instability of two-dimensional panels in uniform incompressible flow. J. Sound Vib. 47, 163–178 (1974)
Bisplinghoff, R.L., Ashley, H., Halfman, R.L.: Aeroelasticity. Addison-Wesley Publishing Co., Inc., Cambridge, MA (1955)
Guo, C.Q., Païdoussis, M.P.: Stability of rectangular plates with free side-edges in two-dimensional inviscid channel flow. J. Appl. Mech. 67, 171–176 (2000)
Li, P., Yang, Y.R., Xu, W.: Nonlinear dynamics analysis of a two-dimensional thin panel with an external forcing in incompressible subsonic flow. Nonlinear Dyn. 67, 2483–2503 (2012)
Li, P., Yang, Y.R., Xu, W., Chen, G.: On the aeroelastic stability and bifurcation structure of subsonic nonlinear thin plates subjected to external excitation. Arch. Appl. Mech. 82, 1251–1267 (2012)
Huang, L.X.: Flutter of cantilevered plates in axial flow. J. Fluids Struct. 9, 127–147 (1995)
de Breuker, R., Abdalla, M.M., Gürdal, Z.: Flutter of partially rigid cantilevered plates in axial flow. AIAA J. 46, 936–946 (2008)
Yang, Y.B., Moretti, P.M.: Flow-induced vibration of free edges of thin films. J. Fluids Struct. 16, 989–1008 (2002)
Watanabe, Y., Suzuki, S., Sugihara, M., Sueoka, Y.: A theoretical study of paper flutter. J. Fluids Struct. 16, 543–560 (2002)
Li, P., Yang, Y.R.: On the stability and chaos of a plate with motion constrains subjected to subsonic flow. Int. J. Non-Linear. Mech. 59, 28–36 (2014)
Ellen, C.H.: The non-linear stability of panels in incompressible flow. J. Sound Vib. 54, 117–121 (1977)
Matsuzaki, Y.: Reexamination of stability of a two-dimensional finite panel exposed to an incompressible flow. Trans. ASME. J. Appl. Mech. 48, 472–478 (1981)
Tang, D.M., Yamamoto, H., Dowell, E.H.: Flutter and limit cycle oscillations of two-dimensional panels in three-dimensional axial flow. J. Fluids Struct. 17, 225–242 (2003)
Attar, P.J., Dowell, E.H., Tang, D.M.: Modeling aerodynamic nonlinearity for two aeroelastic configurations: delta and flapping flag. In: Proceedings of the 44th AIAA/ASME/ASCE/AHS Structure, Structural dynamics and Material Conference, 7–10 April, Norfolk, VA, pp. 1–12 (2003)
Tang, L.S., Païdoussis, M.P.: On the stabilities and the post-critical behavior of two-dimensional cantilevered flexible plates in axial flow. J. Sound Vib. 305, 97–115 (2007)
Tang, L.S., Païdoussis, M.P., Jiang, J.: The dynamics of variants of two-dimensional cantilevered flexible plates in axial flow. J. Sound Vib. 323, 214–231 (2009)
Yang, Y.R.: KBM method of analyzing limit cycle flutter of a wing with an external store and comparison with a wind-tunnel test. J. Sound Vib. 187, 271–280 (1995)
Yang, Z.C., Zhao, L.C.: Analysis of limit cycle flutter of an airfoil in incompressible flow. J. Sound Vib. 123, 1–13 (1988)
Jin, J.D.: Stability and chaotic motions of a restrained pipe conveying fluid. J. Sound Vib. 208, 427–439 (1997)
Païdoussis, M.P., Li, G.X., Rand, R.H.: Chaotic motions of a constrained pipe conveying fluid: comparison between simulation, analysis, and experiment. Trans. ASME. J. Appl. Mech. 58, 559–565 (1991)
Yang, Y.R., Zhao, L.C.: Investigation of subharmonic response of limit cycle flutter of wing-store system. J. Vib. Eng. 5, 296–305 (1992). (in Chinese)
Shaw, S.W., Holmes, P.J.: A periodically forced piece linear oscillator. J. Sound Vib. 90, 129–155 (1983)
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Grant Nos: 11302183; 11372257; 11072204); the Fundamental Research Funds for Central Universities (Grant No: 2682013XC026) and the project for “Youth Science and Technology Innovation Team (2013TD0004) of Sichuan Province, China.” The authors are grateful to the anonymous reviewers whose work helped greatly in writing this paper.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
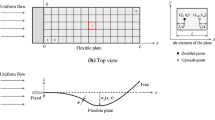
The elements of each matrix in Eq. 8 are defined as follows:
\(\mathbf{M}_\mathrm{s} \) and \(\mathbf{M}_\mathrm{f} \) are \(N\times N\) matrices with the elements:
\(\mathbf{C}_\mathrm{s}\) and \(\mathbf{C}_\mathrm{f}\) are \(N\times N\) matrices with the elements:
\(\mathbf{K}_\mathrm{s}\) and \(\mathbf{K}_\mathrm{f} \) are \(N\times N\) matrices with the elements:
\(\mathbf{F}_{\mathrm{non}} \) is a \(N\times 1\) vector with the elements:
where \(\eta _r\) is the dimensionless plate displacement at \(\xi =\xi _r\):
Appendix 2
The elements of each matrix in Eq. 10 are defined as follows:
Appendix 3
The elements of each matrix in Eq. 22 are defined as follows:
The elements of each matrix in Eq. 24 are defined as follows:
Rights and permissions
About this article
Cite this article
Li, P., Yang, Y. & Chen, G. Analysis of nonlinear limit cycle flutter of a restrained plate induced by subsonic flow. Nonlinear Dyn 79, 119–138 (2015). https://doi.org/10.1007/s11071-014-1650-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-014-1650-4