Skip to main content
SpringerLink
Log in

The velocity difference control signal for two-lane car-following model

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

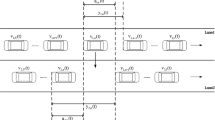
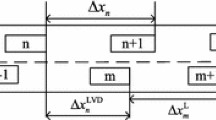
Based on single-lane traffic model, a two-lane traffic model is presented considering the velocity difference control signal. The stability condition of the model is obtained by the control theory. The delayed feedback control signal is added to the two-lane model, and the corresponding stability condition is derived again. The numerical simulations show that as the stability conditions are satisfied, the small disturbance will not amplify with and without control signal. In the meantime, the stability is strengthened as the control signal is considered. So the control signal would suppress the traffic disturbance successfully.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Bando, M., Hasebe, K., Nakayama, A.: Dynamic model of traffic congestion and numerical simulation. Phys. Rev. E 51, 1035–1042 (1995)

    Article  Google Scholar 

  2. Peng, G.H., Cai, X.H., Liu, C.Q., Cao, M.X., Tuo, M.X.: Optimal velocity difference model for a car-following theory. Phys. Lett. A 375, 3973–3977 (2011)

    Article  MATH  Google Scholar 

  3. Ge, H.X., Cheng, R.J., Li, Z.P.: Two velocity difference model for a car following theory. Physica A 387, 5239–5245 (2008)

    Article  Google Scholar 

  4. Li, Z.P., Liu, F.Q.: An improved car-following model for multiphase vehicular traffic flow and numerical tests. Commun. Theor. Phys. 46, 367–373 (2006)

    Article  Google Scholar 

  5. Li, Z.P., Gong, X.B., Liu, Y.C.: A velocity-separation difference model for car-following theory and simulation tests. IEEE ICNSC 2006, 556–561 (2006)

    Google Scholar 

  6. Li, Z.P., Gong, X.B., Liu, Y.C.: A model of car-following with adaptive headway. J. Shanghai Jiao Tong Univ. 11(3), 394–398 (2006)

  7. Jiang, R., Wu, Q.S., Zhu, Z.J.: Full Velocity difference model for car-following theory. Phys. Rev. E 64, 017101–017105 (2001)

    Article  Google Scholar 

  8. Xue, Y.: One-dimensional traffic model to consider priority of the stochastic deceleration. Commun. Theor. Phys. 41, 477–480 (2004)

    Article  MATH  Google Scholar 

  9. Peng, G.H.: A new lattice model of two-lane traffic flow with the consideration of optimal current difference. Commun. Nonlinear Sci. Numer. Simul. 18, 559–566 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  10. Konishi, K.J., Michio, H., Hideki, K.: Decentralized delayed-feedback control of a coupled map model for open flow. Phys. Rev. E 58, 3055–3059 (1998)

    Article  Google Scholar 

  11. Zhao, X.M., Gao, Z.Y.: A control method for congested traffic induced by bottlenecks in the coupled map car-following model. Physica A 366, 513–522 (2006)

    Article  Google Scholar 

  12. Han, X.L., Jiang, C.Y., Ge, H.X., Dai, S.Q.: A modified coupled map car-following model based on application of intelligent transportation system and control of traffic congestion. Acta. Phys. Sin. 56, 4383 (2007). (in Chinese)

    Google Scholar 

  13. Shen, F.Y., Zhang, H., Ge, H.X., Yu, H.M., Lei, L.: A control method for congested traffic in the coupled map car-following model. Chin. Phys. B 18, 4208 (2009)

    Article  Google Scholar 

  14. Yu, H.M., Cheng, R.J., Ge, H.X.: Considering backward effect in coupled map car-following model. Commun. Theor. Phys. 54, 117 (2010)

    Article  MATH  Google Scholar 

  15. Ge, H.X., Cheng, R.J., Li, Z.P.: Considering two-velocity difference effect for coupled map car-following model. Acta. Phys. Sin. 60, 080508 (2011)

  16. Ge, H.X., Yu, J., Lo, S.M.: A control method for congested traffic in the car-following model. Chin. Phys. B 29, 050502 (2012)

  17. Ge, H.X., Meng, X.P., Ma, J., Lo, S.M.: An improved car-following model considering influence of other factors on traffic jam. Physica A 377(1–2), 9–12 (2012)

    Google Scholar 

  18. Chen, X., Gao, Z.Y., Zhao, X.M., Jia, B.: Study on the two-lane feedback controlled car-following model. Acta. Phys. Sin. 56, 2046 (2007). (in Chinese).

    Google Scholar 

  19. Nagatani, T.: Jamming transitions and the modified Korteweg C de Vries equation in a two-lane traffic flow. Physica A 256, 297–310 (1999)

    Article  Google Scholar 

  20. Tang, T.Q., Huang, H.J., Gao, Z.Y.: Stability of the car-following model on two lanes. Phys. Rev. E 72, 066124 (2005)

  21. Tang, T.Q., Huang, H.J., Wong, S.C., Jiang, R.: Lane changing analysis for two-lane traffic flow. Acta. Mech. Sin. 23, 49–54 (2007)

    Article  MATH  Google Scholar 

  22. Shingo, K., Nagatani, T.: Spatio-temporal dynamics of jams in two-lane traffic flow with a blockage. Physica A 318, 537–550 (2003)

    Article  MATH  Google Scholar 

  23. Zheng, L., Ma, S.F., Zhong, S.Q.: Influence of lane change on stability analysis for two-lane traffic flow. Chin. Phys. B 20, 088701 (2011)

    Article  Google Scholar 

Download references

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos. 11262003, 11302125 and 11372166 Shanghai Science and Technology Commission (No. 12PJ1404000)), the Scientific Research Fund of Zhejiang Provincial, China (Grant No. LY13A010005) and the K.C. Wong Magna Fund in Ningbo University, China.

Author information

Authors and Affiliations

  1. Faculty of Science, Ningbo University, Ningbo , 315211, China

    Yu Cui

  2. Department of Fundamental Course, Ningbo Institute of Technology, Zhejiang University, Ningbo , 315100, China

    Rong-Jun Cheng

  3. Faculty of Maritime and Transportation, Ningbo University, Ningbo , 315211, China

    Hong-Xia Ge

  4. National Traffic Management Engineering & Technology Research Centre, Ningbo University Sub-centre, Ningbo , 315211, China

    Hong-Xia Ge

  5. Jiangsu Province Collaborative Innovation Center for Modern Urban Traffic Technologies, Nanjing , 210096, China

    Hong-Xia Ge

Authors
  1. Yu Cui
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rong-Jun Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hong-Xia Ge
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hong-Xia Ge.

Appendices

Appendix 1

In this appendix, we present details of linearization and Laplace transformation.

According to the control theory, the vehicular dynamics described by Eq. (4) can be rewritten as a linear time-invariant system, that is

$$\begin{aligned}&\!\!\!\left[ \begin{array}{l} \mathrm{d}v_{l,n}^{0}(t)/dt\\ \mathrm{d}y_{l,n}^{0}(t)/dt\\ \mathrm{d}y_{l,n-1}^{0}(t)/dt\\ \mathrm{d}q_{l,n}^{0}(t)/dt\\ \mathrm{d}q_{l,n+1}^{0}(t)/dt \end{array}\right] \nonumber \\&=\quad \left[ \begin{array}{lllll} -a_l &{} a_l\varLambda _{n,l}^{y_1} &{} a_l\varLambda _{n,l}^{y_2} &{}a_l\varLambda _{n,l}^{q_1}&{} a_l\varLambda _{n,l}^{q_2}\\ -1 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ -1 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array}\right] \left[ \begin{array}{l} v_{l,n}^0(t)\\ y_{l,n}^0(t)\\ y_{l,n-1}^0(t)\\ q_{l,n}^0(t)\\ q_{l,n+1}^0(t)\\ \end{array}\right] \nonumber \\&\quad \!\!\!+\left[ \begin{array}{l} 0\\ 1\\ -1\\ 0\\ 0\\ \end{array}\right] v_{l,n-1}^0(t)+ \left[ \begin{array}{l} 0\\ 0\\ 1\\ 0\\ 0\\ \end{array}\right] v_{l,n-2}^0(t) + \left[ \begin{array}{l} 0\\ 0\\ 0\\ 1\\ 0\\ \end{array}\right] v_{l,n}^{f0}(t)\nonumber \\&\quad \!\!\!+ \left[ \begin{array}{l} 0\\ 0\\ 0\\ 0\\ 1\\ \end{array}\right] v_{l,n+1}^{f0}(t) + \left[ \begin{array}{l} 0\\ 0\\ 0\\ 1\\ 1\\ \end{array}\right] \Delta v^{*}. \end{aligned}$$
(19)

Taking Laplace transformation, we have

$$\begin{aligned}&\!\!\!s\left[ \begin{array}{l} V_{l,n}^0(s)\\ Y_{l,n}^0(s) \\ Y_{l,n-1}^0(s) \\ Q_{l,n}^0(s)\\ Q_{l,n+1}^0(s)\\ \end{array}\right] \nonumber \\&\!\!\!\quad =\left[ \begin{array}{lllll} -a_l &{} a_l\varLambda _{n,l}^{y_1} &{} a_{n,l}\varLambda _l^{y_2} &{}a_l\varLambda _{n,l}^{q_1}&{} a_l\varLambda _{n,l}^{q_2}\\ -1 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0&{} 0\\ -1 &{}0&{} 0 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array}\right] \left[ \begin{array}{l} V_{l,n}^0(s)\\ Y_{l,n}^0(s)\\ Y_{l,n-1}^0(s)\\ Q_{l,n}^0(s)\\ Y_{l,n+1}^o(s)\\ \end{array}\right] \nonumber \\&\qquad \!\!\!+\left[ \begin{array}{l} 0\\ 1\\ -1\\ 0\\ 0\\ \end{array}\right] V_{l,n-1}^0(s){+} \left[ \begin{array}{l} 0\\ 0\\ 1\\ 0\\ 0\\ \end{array}\right] V_{l,n-2}^0(s) {+} \left[ \begin{array}{l} 0\\ 0\\ 0\\ 1\\ 0\\ \end{array}\right] V_{l,n}^{f0}(s)\nonumber \\&\qquad \!\!\!+ \left[ \begin{array}{l} 0\\ 0\\ 0\\ 0\\ 1\\ \end{array}\right] V_{l,n+1}^{f0}(s) + \left[ \begin{array}{l} 0\\ 0\\ 0\\ 1\\ 1\\ \end{array}\right] \Delta V^{*}, \end{aligned}$$
(20)

where \(V_{l,n}^0(s)=L(v_{l,n}^0(t))\), \(V_{l,n-1}^0(s)=L(v_{l,n-1}^0(t))\), \(V_{l,n-2}^0(s)=L(v_{l,n-2}^0(t))\), \(V_{l,n}^{f0}(s)=L(v_{l,n}^{f0}(t))\), \(V_{l,n+1}^{f0}(s)=L(v_{l,n+1}^{f0}(t))\), \(Y_{l,n}^0(s)=L(y_{l,n}^0(t))\), \(Y_{l,n-1}^0(s)=L(y_{l,n-1}^0(t))\), \(Q_{l,n}^0(s)=L(q_{l,n}^0(t))\), \(Q_{l,n+1}^0(s)=L(q_{l,n+1}^0(t))\), \(\Delta V^*=L(\Delta v^*)\), \(L(\cdot )\) denotes the Laplace transformation. After derivation of Eq. (23), we have the following transfer relationship:

$$\begin{aligned} V_{l,n}^0(s)&= \frac{a_{l}(\varLambda _{n,l}^{y_1}-\varLambda _{n,l}^{y_2})}{s^2+a_ls+\varLambda _{n,l}^{y_1}+\varLambda _{n,l}^{q_1}-\varLambda _{n,l}^{q_2}} V_{l,n-1}^0(s)\nonumber \\&+\frac{a_l\varLambda _{n,l}^{y_2}}{s^2+a_ls+\varLambda _{n,l}^{y_1} +\varLambda _{n,l}^{q_1}-\varLambda _{n,l}^{q_2}}V_{l,n-2}^0(s)\nonumber \\&+\frac{a_l\varLambda _{n,l}^{y_2}}{s^2+a_ls+\varLambda _{n,l}^{y_1}+\varLambda _{n,l}^{q_1} -\varLambda _{n,l}^{q_2}}V_{l,n}^{f0}(s)\nonumber \\&-\frac{a_l\varLambda _{n,l}^{q_1}}{s^2+a_ls+\varLambda _{n,l}^{y_1} +\varLambda _{n,l}^{q_1}-\varLambda _{n,l}^{q_2}}V_{l,n+1}^{f0}(s)\nonumber \\&+\frac{a_l\varLambda _{n,l}^{q_1}-a_l\varLambda _{n,l}^{q_2}}{s^2+a_ls+\varLambda _{n,l}^{y_1} +\varLambda _{n,l}^{q_1}-\varLambda _{n,l}^{q_2}}\Delta V^{*} \end{aligned}$$
(21)

and

$$\begin{aligned} V_{l,n}^0(s)=G_l(s)V_{l,n-1}^0(s). \end{aligned}$$
(22)

Appendix 2

In this appendix, we present details of linearization and Laplace transformation with control signals. Eq. (12) can be given as

$$\begin{aligned}&\!\!\!\left[ \begin{array}{l} \frac{\mathrm{d}v_{l,n}^{0}(t)}{\mathrm{d}t}\\ \frac{\mathrm{d}y_{l,n}^{0}(t)}{\mathrm{d}t}\\ \frac{\mathrm{d}y_{l,n-1}^{0}(t)}{\mathrm{d}t}\\ \frac{\mathrm{d}q_{l,n}^{0}(t)}{\mathrm{d}t}\\ \frac{\mathrm{d}q_{l,n+1}^{0}(t)}{\mathrm{d}t}\\ \end{array}\right] \nonumber \\&\!\!\!\quad =\left[ \begin{array}{lllll} -a_l-k_n^{y_1}-k_n^{q_1}+k_n^{q_2} &{} a_l\varLambda _{n,l}^{y_1} &{} a_l\varLambda _{n,l}^{y_2} &{}a_l\varLambda _{n,l}^{q_1}&{} a_l\varLambda _{n,l}^{q_2}\\ -1 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ -1 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array}\right] \nonumber \\&\times \left[ \begin{array}{l} v_{l,n}^0(t)\\ y_{l,n}^0(t)\\ y_{l,n-1}^0(t)\\ q_{l,n}^0(t)\\ q_{l,n+1}^0(t)\\ \end{array}\right] \nonumber \\&\quad \!\!\!+\left[ \begin{array}{l} k_n^{y_1}-k_n^{y_2}\\ 1\\ -1\\ 0\\ 0\\ \end{array}\right] v_{l,n-1}^0(t)+ \left[ \begin{array}{l} k_n^{y_2}\\ 0\\ 1\\ 0\\ 0\\ \end{array}\right] v_{l,n-2}^0(t)\nonumber \\&\!\!\!\quad +\left[ \begin{array}{l} k_n^{q_1}\\ 0\\ 0\\ 1\\ 0\\ \end{array}\right] v_{l,n}^{f0}(t) {+}\left[ \begin{array}{l} k_n^{q_2}\\ 0\\ 0\\ 0\\ 1\\ \end{array}\right] v_{l,n+1}^{f0}(t) {+}\left[ \begin{array}{l} 0\\ 0\\ 0\\ 1\\ 1\\ \end{array}\right] \Delta v^{*}. \end{aligned}$$
(23)

After Laplace transformation, we have

$$\begin{aligned}&\!\!\!s\left[ \begin{array}{l} V_{l,n}^0(s)\\ Y_{l,n}^0(s) \\ Y_{l,n-1}^0(s) \\ Q_{l,n}^0(s)\\ Q_{l,n+1}^0(s)\\ \end{array}\right] \nonumber \\&\quad =\left[ \begin{array}{lllll} -a_l-k_n^{y_1}-k_n^{q_1}+k_n^{q_2} &{} a_l\varLambda _{n,l}^{y_1} &{} a_l\varLambda _{n,l}^{y_2} &{}a_l\varLambda _{n,l}^{q_1}&{} a_l\varLambda _{n,l}^{q_2}\\ -1 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ -1 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array}\right] \nonumber \\&\qquad \left[ \begin{array}{l} V_{l,n}^0(s)\\ Y_{l,n}^0(s)\\ Y_{l,n-1}^0(s)\\ Q_{l,n}^0(s)\\ Q_{l,n-1}^0(s)\\ \end{array}\right] \nonumber \\&\quad +\left[ \begin{array}{l} k_n^{y_1}-k_n^{y_2}\\ 1\\ -1\\ 0\\ 0\\ \end{array}\right] V_{l,n-1}^0(s)+ \left[ \begin{array}{l} k_n^{y_2}\\ 0\\ 1\\ 0\\ 0\\ \end{array}\right] V_{l,n-2}^0(s) + \left[ \begin{array}{l} k_n^{q_1}\\ 0\\ 0\\ 1\\ 0\\ \end{array}\right] V_{l,n}^{f0}(s)\nonumber \\&\quad +\left[ \begin{array}{l} k_n^{q_2}\\ 0\\ 0\\ 0\\ 1\\ \end{array}\right] V_{l,n+1}^{f0}(s) +\left[ \begin{array}{l} 0\\ 0\\ 0\\ 1\\ 1\\ \end{array}\right] \Delta V^{*}. \end{aligned}$$
(24)

So we have the following transfer relationship:

$$\begin{aligned}&\!\!\!\!V_{l,n}^0(s)\nonumber \\&\!\!\!\!\quad =\frac{a_{l}(\varLambda _{n,l}^{y_1}-\varLambda _{n,l}^{y_2})+ k_n^{y_1}-k_n^{y_2}}{s^2+(a_l+k_n^{y_1}+k_n^{q_1}-k_n^{q_2})s+ \varLambda _{n,l}^{y_1}+\varLambda _{n,l}^{q_1}-\varLambda _{n,l}^{q_2}}V_{l,n-1}^0(s)\nonumber \\&\!\!\!\!\qquad +\frac{a_l\varLambda _{n,l}^{y_2}+k_n^{y_2}}{s^2+(a_l+k_n^{y_1}+k_n^{q_1}-k_n^{q_2})s +\varLambda _{n,l}^{y_1}+\varLambda _{n,l}^{q_1}-\varLambda _{n,l}^{q_2}}V_{l,n-2}^0(s)\nonumber \\&\!\!\!\!\qquad +\frac{a_l\varLambda _{n,l}^{y_2}+k_n^{q_1}}{s^2+(a_l+k_n^{y_1}+k_n^{q_1}-k_n^{q_2})s +\varLambda _{n,l}^{y_1}+\varLambda _{n,l}^{q_1}-\varLambda _{n,l}^{q_2}}V_{l,n}^{f0}(s)\nonumber \\&\!\!\!\!\qquad -\frac{a_l\varLambda _{n,l}^{q_1}+k_n^{q_2}}{s^2+(a_l+k_n^{y_1}+k_n^{q_1}-k_n^{q_2})s +\varLambda _{n,l}^{y_1}+\varLambda _{n,l}^{q_1}-\varLambda _{n,l}^{q_2}}V_{l,n+1}^{f0}(s)\nonumber \\&\!\!\!\!\qquad +\frac{a_l\varLambda _{n,l}^{q_1}-a_l\varLambda _{n,l}^{q_2}}{s^2+(a_l+k_n^{y_1}+k_n^{q_1} -k_n^{q_2})s+\varLambda _{n,l}^{y_1}+\varLambda _{n,l}^{q_1}-\varLambda _{n,l}^{q_2}}\Delta V^{*},\nonumber \\ \end{aligned}$$
(25)
$$\begin{aligned}&\!\!\!\!V_i^0(s)=T^*(s)V_{i+n-1}^0(s). \end{aligned}$$
(26)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cui, Y., Cheng, RJ. & Ge, HX. The velocity difference control signal for two-lane car-following model. Nonlinear Dyn 78, 585–596 (2014). https://doi.org/10.1007/s11071-014-1462-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-014-1462-6

Keywords

Search

Navigation