Skip to main content
SpringerLink
Log in

Bifurcations of backbone curves for systems of coupled nonlinear two mass oscillator

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

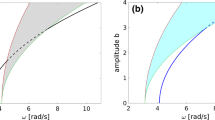
This paper considers the dynamic response of coupled, forced and lightly damped nonlinear oscillators with two degree-of-freedom. For these systems, backbone curves define the resonant peaks in the frequency–displacement plane and give valuable information on the prediction of the frequency response of the system. Previously, it has been shown that bifurcations can occur in the backbone curves. In this paper, we present an analytical method enabling the identification of the conditions under which such bifurcations occur. The method, based on second-order nonlinear normal forms, is also able to provide information on the nature of the bifurcations and how they affect the characteristics of the response. This approach is applied to a two-degree-of-freedom mass, spring, damper system with cubic hardening springs. We use the second-order normal form method to transform the system coordinates and identify which parameter values will lead to resonant interactions and bifurcations of the backbone curves. Furthermore, the relationship between the backbone curves and the complex dynamics of the forced system is shown.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Arnold, V.I., Levi, M., Szücs, J.: Geometrical Methods in the Theory of Ordinary Differential Equations. Springer, New York (2012)

    Google Scholar 

  2. Cartmell, M.: Introduction to Linear, Parametric and Nonlinear Vibrations. Chapman and Hall, London (1990)

    MATH  Google Scholar 

  3. Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York (1983)

    Book  MATH  Google Scholar 

  4. Nayfeh, A.H., Pai, P.F.: Linear and Nonlinear Structural Mechanics. Wiley, New York (2008)

    Google Scholar 

  5. Thompson, J.M.T., Stewart, H.B.: Nonlinear Dynamics and Chaos. Wiley, Chichester (2002)

    MATH  Google Scholar 

  6. Wagg, D.J., Neild, S.A.: Nonlinear Vibration with Control: For Flexible and Adaptive Structures. Springer, New York (2009)

    Google Scholar 

  7. Neild, S.A., Wagg, D.J.: Applying the method of normal forms to second order nonlinear vibration problems. Proc. R. Soc. A 467, 1141–1163 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  8. Lewandowski, R.: Solutions with bifurcation points for free vibration of beams: an analytical approach. J. Sound Vib. 177, 239–249 (1994)

    Article  MATH  Google Scholar 

  9. Lewandowski, R.: On beams membranes and plates vibration backbone curves in cases of internal resonance. Meccanica 31, 323–346 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  10. Kerschen, G., Peeters, M., Golinval, J.C., Vakakis, A.F.: Nonlinear normal modes, Part I: a useful framework for the structural dynamicist. Mech. Syst. Signal Process. 23, 170–194 (2009)

    Article  Google Scholar 

  11. Rand, R.H.: Lecture notes on nonlinear vibrations. Dept. Theoretical & Applied Mechanics, Cornell University, Ithaca, NY. http://www.tam.cornell.edu/randdocs (2005)

  12. Vakakis, A.F., Manevitch, L.I., Mikhlin, Y.V., Pilipchuk, V.N., Zevin, A.A.: Normal Modes and Localization in Nonlinear Systems. Wiley, New York (1996)

    Book  MATH  Google Scholar 

  13. Nayfeh, A.H., Lacarbonara, W., Chin, C.M.: Nonlinear normal modes of buckled beams: three-to-one and one-to-one internal resonances. Nonlinear Dynam. 18, 253–273 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  14. Jezequel, L., Lamarque, C.: Analysis of non-linear dynamical systems by the normal form theory. J. Sound Vib. 149(3), 429–459 (1991)

    Article  Google Scholar 

  15. Touzé, C., Thomas, O., Chaigne, A.: Hardening/softening behaviour in non-linear oscillations of structural systems using non-linear normal modes. J. Sound Vib. 273(1), 77–101 (2004)

    Article  Google Scholar 

  16. Neild, S.A.: Approximate methods for analysing nonlinear structures. In: Wagg, D.J., Virgin, L. (eds.) Exploiting Nonlinear Behavior in Structural Dynamics, pp. 53–109. Springer, Vienna (2012)

    Chapter  Google Scholar 

  17. Neild, S.A., Wagg, D.J.: A generalized frequency detuning method for multidegree-of-freedom oscillators with nonlinear stiffness. Nonlinear Dyn. 73, 649–663 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  18. Nayfeh, A.H.: Method of Normal Forms. Wiley, New York (1993)

    MATH  Google Scholar 

  19. Vakakis, A.F., Rand, R.H.: Normal modes and global dynamics of a two-degree-of-freedom non-linear system. Low energies. Int. J. Nonlinear Mech. 27, 861–874 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  20. Xin, Z.F., Neild, S.A., Wagg, D.J., Zuo, Z.X.: Resonant response functions for nonlinear oscillators with polynomial type nonlinearities. J. Sound Vib. 332, 1777–1788 (2013)

    Article  Google Scholar 

  21. Lust, K.: Improved numerical Floquet multipliers. Int. J. Bifurcat. Chaos 11, 2389–2410 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  22. Chicone, C.: Ordinary Differential Equations with Applications. Springer, New York (2006)

    MATH  Google Scholar 

  23. Doedel, E.J., Champneys, A.R., Fairgrieve, T.F., Kuznetsov, Y.A., Dercole, F., Oldeman, B.E., Paffenroth, R.C., Sandstede, B., Wang, X.J., Zhang, C.: AUTO-07P: Continuation and Bifurcation software for ordinary differential equations. Concordia University, Montreal. http://cmvl.cs.concordia.ca (2008)

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Bristol, Bristol , BS8 1TR, UK

    A. Cammarano, T. L. Hill & S. A. Neild

  2. Department of Mechanical Engineering, University of Sheffield, Sheffield , S1 3JD, UK

    D. J. Wagg

Authors
  1. A. Cammarano
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. L. Hill
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. A. Neild
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. D. J. Wagg
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Cammarano.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Cammarano, A., Hill, T.L., Neild, S.A. et al. Bifurcations of backbone curves for systems of coupled nonlinear two mass oscillator. Nonlinear Dyn 77, 311–320 (2014). https://doi.org/10.1007/s11071-014-1295-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-014-1295-3

Keywords

Search

Navigation