Sticking and nonsticking orbits for a two-degree-of-freedom oscillator excited by dry friction and harmonic loading

Abstract

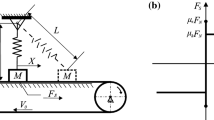
We consider a system composed of two masses connected by linear springs. One of the masses is in contact with a rough surface. Friction force, with Coulomb’s characteristics, acts between the mass and the surface. Moreover, the mass is also subjected to a harmonic external force. Several periodic orbits are obtained in closed form. A first kind of orbits involves sticking phases: during these parts of the orbit, the mass in contact with the rough surface remains at rest for a finite time. Another kind of orbits includes one or more stops of the mass with zero duration. Normal and abnormal stops are obtained. Moreover, for some of these periodic solutions, we prove that symmetry in space and time occurs.

Appendix 1

$$\begin{aligned} H_{i} (t)&= \Lambda B_i (t)\Lambda ^{-1},\,(i=1,2,3) \nonumber \\ B_{2} (t)&= \left( {\begin{array}{ll} s_{1} /\omega _1 &{}\quad 0 \\ 0 &{}\quad s_2 /\omega _2 \\ \end{array}} \right) ,\;s_j =\sin (\omega _j t)\;(j=1,2) \nonumber \\ B_{1} (t)&= B^{\prime }_2 (t),\;B_3 (t)=B^{\prime \prime }_2 (t) \end{aligned}$$

(55)

The natural frequencies ($\omega _{1},~\omega _{2})$ are the roots of the characteristic equation:

$$\begin{aligned} D(s^{2})\equiv \det (K-Is^{2})=0,\quad K=\left( {\begin{array}{l} \;1\quad \quad -\chi \\ -\chi \eta \;\;\chi \eta \\ \end{array}} \right) \nonumber \\ \end{aligned}$$

(56)

The eigenvectors $\psi _j =\left( {\begin{array}{l} 1 \\ \lambda _j \\ \end{array}} \right) ,(j=1,2)$ are defined by ($K~-~I\omega _{j}^{2})\psi _{j}~=~0$

These matrices fulfil the following property

$$\begin{aligned}&H_1^2 (t)-H_2 (t)H_3 (t)=0\end{aligned}$$

(57)

$$\begin{aligned}&\Gamma _i (t)=\Sigma \gamma _i (t)\Sigma ^{-1},\quad (i=1,2,3) \nonumber \\&\gamma _2 (t)=\left( {\begin{array}{ll} \sin t\quad 0 \\ 0\quad \quad \;t \\ \end{array}} \right) ,\quad \Sigma =\left( {\begin{array}{l} 1\;\;\chi \\ 0\;\;1 \\ \end{array}} \right) \nonumber \\&\gamma _1 (t)=\gamma ^{\prime }_2 (t),\;\gamma _3 (t)=\gamma ^{\prime \prime }_2 (t) \end{aligned}$$

(58)

The matrices $\Gamma _{i}(t)$ fulfil also the property

$$\begin{aligned}&\Gamma _1^2 (t)-\Gamma _2 (t)\Gamma _3 (t)=0 \end{aligned}$$

(59)