Suppression of harmonic perturbations and bifurcation control in tracking objectives of a boiler–turbine unit in power grid

Abstract

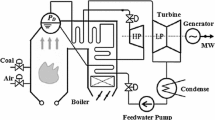
In the presence of harmonic disturbances, boiler–turbine units may demonstrate quasi-periodic behaviour due to the occurrence of various types of bifurcation. In this article, a nonlinear model of boiler–turbine unit is considered in which drum pressure, electric output and drum water level are controlled via manipulation of valve positions for fuel, steam and feed-water flow rates. For bifurcation control in tracking problem, two controllers are designed based on gain scheduling and feedback linearization (FBL). To investigate the efficiency of control strategies, three cases are considered for desired tracking objectives (a sequence of steps, ramps/steps, and a combination of them). According to the results, FBL controller works successfully in suppression of harmonic perturbations and consequently bifurcation control. As it is implemented, quasi-periodic solutions (caused by Hopf bifurcation) are vanished; leading to the appearance of periodic solutions with low amplitudes. Consequently, appropriate tracking performance with less oscillatory behaviour is observed for the drum pressure, electric output, and drum water level (desirable for the power grid). In addition, when FBL controller is used, less control efforts are predicted for the bifurcation control.

Appendices

Appendix 1: Design of controller based on feedback linearization

In feedback linearization (FBL) approach, the nonlinear terms of the dynamic system are eliminated by means of state variables feedback. Then a suitable controller is designed to stabilize the desired trajectories of the system [31]. In this section, a brief overview on the design of FBL controller is presented. More details of this approach were discussed in [29]. Consider a square MIMO system in the neighbourhood of the operating point $\bar{{x}}^{0}$ as [31]

$$\begin{aligned} \dot{\bar{{x}}}=\Phi (\bar{{x}})+\Psi (\bar{{x}}) \bar{{u}}; \bar{{y}}=\mathrm{H}(\bar{{x}}) \end{aligned}$$

(10)

where $\bar{{x}}$ is $n \times 1$ the state vector, $\bar{{u}}$ is $r \times 1$ control input vector,$\bar{{y}}$ is $m \times 1$ outputs vector; $\Phi$ and H are smooth vector fields and $\Psi$ is a $n \times r$ smooth matrix (in this paper, $m = r =3$). Assume that $\delta _{i}$ is the smallest integer that at least one of the inputs appears in $y_i ^{(\delta _i )}$, then (in this paper, $y_{i}^{(j)}$ represents the $j$ order differentiation of $y_{i}$):

$$\begin{aligned} y_i ^{(\delta _i )}=L_{\Phi ^{\delta _i }} \mathrm{H}_i +\sum _{j=1}^r {L_{\Psi _j } L_{\Phi ^{\delta _i -1}} \mathrm{H}_i u_j } \end{aligned}$$

(11)

with repeated Lie derivatives $L_{\Psi _j } L_{\Phi ^{\delta _i -1}} \mathrm{H}_i (x)\ne 0$ for at least one $j$ in the vicinity of $\bar{{x}}^{0}$; while Lie derivative of H with respect to $\Phi$ is a scalar function defined as:

$$\begin{aligned} L_\Phi \mathrm{H}&= \nabla \mathrm{H} \cdot \Phi ; L_{\Phi ^{0}} \mathrm{H}=\mathrm{H}\nonumber \\ L_{\Phi ^{i}} \mathrm{H}&= L_\Phi (L_{\Phi ^{i-1}} \mathrm{H})=\nabla (L_{\Phi ^{i-1}} \mathrm{H})\cdot \Phi . \end{aligned}$$

(12)

Similarly, if $\Psi$ is another vector field, then the scalar function $L_{\Psi }L_{\Phi }$H$(x)$ is

$$\begin{aligned} L_\Psi L_\Phi \hbox {H}=\nabla (L_\Phi \mathrm{H})\cdot \Psi . \end{aligned}$$

(13)

Applying the same procedure for each output $y_{i}$, yields

$$\begin{aligned} \left[ {y_1 ^{(\delta _1 )}\ldots y_m ^{(\delta _m )}} \right] ^{T}&= \left[ {L_{\Phi ^{\delta _1 }} \mathrm{H}_1 (\bar{{x}})}\quad {L_{\Phi ^{\delta _2 }} \mathrm{H}_2 (\bar{{x}})}\right. \nonumber \\&\quad \left. \ldots {L_{\Phi ^{\delta _m }} \mathrm{H}_m (\bar{{x}})} \right] ^{T}+\mathrm{N}(\bar{{x}}) \bar{{u}}.\nonumber \\ \end{aligned}$$

(14)

If $\mathrm{N} (\bar{{x}})$ is invertible over the region $\Omega$, the input transformation

$$\begin{aligned} \bar{{u}}&= \mathrm{N}^{-1} \left[ {v_1 -L_{\Phi ^{\delta _1}} \mathrm{H}_1}\quad {v_2 -L_{\Phi ^{\delta _2 }} \mathrm{H}_2}\right. \nonumber \\&\qquad \quad \left. \cdots \, {v_m -L_{\Phi ^{\delta _m }} \mathrm{H}{ }_m}\right] ^{T} \end{aligned}$$

(15)

yields a simpler form of $m$equations as

$$\begin{aligned} y_i ^{(\delta _i )}=v_i. \end{aligned}$$

(16)

In this research, it is assumed that the third state variable $(x_{3})$ is measured either directly or by estimation through a robust state observer (with a general design as presented in the previous research [28]). To avoid tedious computations caused by differentiation of $y_{3}$ as given in Eq. (2), third state variable is chosen as the third output (instead of water level of drum, the fluid density is considered as the third output,$y_{3} = x_{3}$). Through simulations, it can be shown that this definition of $y_{3}$ will not affect the control of real output (i.e., drum water level) represented by Eq. (2). The validity of this assumption was discussed in [29]. Following the same procedure given above (while $\delta _{i}=1$), FBL control laws are determined for the dynamic system of Eq. (1) as [29]:

$$\begin{aligned}&\!\!\!\left[ {{\begin{array}{ccc} {u_1 }&{} {u_2 }&{} {u_3 } \\ \end{array} }} \right] ^{T}\nonumber \\&\quad =\mathrm{N}^{-1}\left[ {{\begin{array}{ccc} {v_1 }&{} {v_2 +\beta _3 x_2 +\beta _2 x_1 ^{9/8}}&{} {v_3 -\frac{\gamma _3 }{\gamma _4 }x_1 } \nonumber \\ \end{array} }} \right] ^{T} ; \\&\qquad \mathrm{N}=\;\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {\alpha _2 }&{} {-\alpha _2 x_1 ^{9/8}}&{} {-\alpha _3 } \\ 0&{} {\beta _1 x_1 ^{9/8}}&{} 0 \\ 0&{} {-({\gamma _2 }/{\gamma _4 }) x_1 }&{} {({\gamma _1 }/{\gamma _4 })} \\ \end{array} }} \right] \end{aligned}$$

(17)

after decoupling the outputs dynamics (Eq. 16), a PI controller is designed as:

$$\begin{aligned} v_i =-K_{1i} e_i -K_{2i} \sigma _i ,\quad \dot{\sigma }_i =e_i =y_i -r_i \end{aligned}$$

(18)

where $r_{i}$ is the command input signal that is desired to be tracked (Fig. 4). Differentiating from Eq. (16), using Eq. (18), and transforming the result into the Laplace domain, yields

$$\begin{aligned} \frac{Y_i (s)}{R_i (s)}=\frac{K_{1i} s+K_{2i} }{s^{2}+K_{1i} s+K_{2i}}. \end{aligned}$$

(19)

To have a characteristic equation similar to the standard second-order system as:

$$\begin{aligned} s^{2}+2\zeta \omega _n s+\omega _n ^{2}=0,\,\omega _n >0,\,0<\zeta <1. \end{aligned}$$

(20)

Control signal gains must be adjusted as

$$\begin{aligned} K_{1i} =2\zeta _i \omega _i , \; K_{2i} =\omega _i ^{2}. \end{aligned}$$

(21)

Appendix 2: Structure of the feedback control law in MIMO system

Dynamic model of boiler–turbine unit is of rank $n=3$. Since the controllability matrix

$$\begin{aligned} {\mathbb {C}}= [B\quad AB\quad A^{2}B \ldots \quad A^{n-1}B]\quad \end{aligned}$$

is of rank 3, dynamic system is completely state controllable. Using the similarity transformation $\mathfrak {R}$ as $\bar{{x}}= \mathfrak {R}\bar{{z}}$, Eq. (5) is represented as:

$$\begin{aligned}&\dot{\bar{{z}}}_\delta = \hat{{A}}_G \bar{{z}}_\delta + \hat{{B}}_G \bar{{u}}_\delta \nonumber \\&\hat{{A}}_G = \mathfrak {R}^{-1}A \mathfrak {R}, \hat{{B}}_G = \mathfrak {R}^{-1} B \end{aligned}$$

(22)

where $\bar{{z}}_\delta$ is the new introduced state vector. Also, using the following transformations:

$$\begin{aligned} \bar{{u}}_\delta = F \bar{{w}}_\delta ; \bar{{w}}_\delta = \bar{{v}}_\delta - P \bar{{z}}_\delta . \end{aligned}$$

(23)

Equation (22) is described as:

$$\begin{aligned}&\dot{\bar{{z}}}_\delta = A_G \bar{{z}}_\delta +B_G \bar{{v}}_\delta \nonumber \\&A_G =\hat{{A}}_G - \hat{{B}}_G FP, B_G =\hat{{B}}_G F \end{aligned}$$

(24)

where $\bar{{v}}_\delta$ is the new control input vector and $A_{G}, B_{G}$ has the general canonical form with elements of $[A_i ]_{\gamma _i \times \gamma _i }\, , \,[B_i ]_{\gamma _i \times 1} ,\,i =1,2,..,r$ and $\sum _{i=1}^{r} \gamma _{i} = n$ as [32]:

$$\begin{aligned} A_G&= \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} [A_1 ]&{}0&{} \ldots &{}0 \\ 0&{}[A_2 ]&{}\ldots &{}0 \\ &{}&{}.&{} \\ 0&{}0&{}\ldots &{}[A_r ] \\ \end{array}} \right] _{n\times n},\nonumber \\ B_G&= \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} [B_1 ]&{}0&{}\cdots &{}0 \\ 0&{}[B_2 ]&{}\cdots &{}0 \\ &{}&{}.&{} \\ 0&{}0&{} \cdots &{} [B_r ] \\ \end{array}} \right] _{n\times r}, \nonumber \\ \left[ A_i\right]&= \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0&{}1&{}0&{}\cdots &{}0 \\ 0&{}0&{}1&{}\cdots &{}0 \\ &{}&{}&{}.&{} \\ 0&{}0&{}0&{}\cdots &{}1 \\ 0&{}0&{}0&{}\cdots &{}0 \\ \end{array}} \right] _{\gamma _i \times \gamma _i }, [B_i ]=\left[ {\begin{array}{l} 0 \\ 0 \\ . \\ . \\ 1 \\ \end{array}} \right] _{\gamma _i \times 1} \end{aligned}$$

(25)

where $r$ is the number of input variables (in this case, $r=3$). Introducing the modified controllability matrix as:

$$\begin{aligned} \bar{{\mathbb {C}}}&= [b_1 b_2\,...\,b_\mathrm{r} \vdots Ab_1 Ab_2\,...\,Ab_\mathrm{r}\vdots \, \ldots \,\vdots A^{n-r}b_1\\&\quad A^{n-r}b_2\,...\,A^{n-r}b_\mathrm{r}] \end{aligned}$$

where $b_{i}$ are the columns of matrix $B$ given by Eq. (6); regular basis of $\bar{{\mathbb {C}}}$ is developed as

$$\begin{aligned} \hat{{ \mathbb {C}}}&= [b_1\,Ab_1\,...\,A^{\gamma _1 -1}b_1\vdots \,b_2\,Ab_2\,...\,A^{\gamma _2-1}b_2\vdots \,...\,\vdots b_r\nonumber \\&\quad Ab_\mathrm{r}\,...\,A^{\gamma _r -1}b_\mathrm{r} ] \end{aligned}$$

(26)

where each column, $A^{j}b_{i}, i = 1,...,r, j = 0,..., r$, is independent from its previous columns. Inverse of $\hat{{\mathbb {C}}}$ given by Eq. (26) is displayed as ([]$^{\prime }$ stands for transpose of the [] quantity):

$$\begin{aligned} \hat{{\mathbb {C}}}^{-1}=\left[ {{e}'_{11}\,..\,{e}'_{1\gamma _1 } \vdots {e}'_{21}\,...\,{e}'_{2\gamma _2 } \vdots \,...\,\vdots {e}'_{r1}\,...\,{e}'_{r\gamma _r } } \right] ^{\prime }. \end{aligned}$$

Similarity transformation $\mathfrak {R}$ is defined as [32]:

$$\begin{aligned} \mathfrak {R}&= \left( \left[ {e}'_{1\gamma _1 } {e}'_{1\gamma _1 } A,\,...\,{e}'_{1\gamma _1 } A^{\gamma _1 -1} \vdots {e}'_{2\gamma _2 } {e}'_{2\gamma _2 } A\,...\,{e}'_{2\gamma _2 } \right. \right. \nonumber \\&\quad \left. \left. A^{\gamma _2 -1} \,\vdots \ldots \vdots \, {e}'_{r\gamma _r } {e}'_{r\gamma _r } A\,...\, {e}'_{r\gamma _r } A^{\gamma _r -1}\right] ^{\prime }\right) ^{-1}.\nonumber \\ \end{aligned}$$

(27)

Considering again Eq. (24) and constructing the feedback control law as $v_{\delta }=-\Gamma z_{\delta }$, yields:

$$\begin{aligned} \dot{\bar{{z}}}_\delta = A_d \bar{{z}}_\delta , A_d =A_G -B_G \Gamma \end{aligned}$$

(28)

where $A_{d}$ is the desired state matrix including coefficients representing desired closed loop poles $({\vert }{ sI}-A_{d}{\vert }=(s-\mu _{1})(s-\mu _{2})\ldots (s-\mu _{n}))$; having the general form of $A_{G}$ as given by Eq. (25). Considering Eqs. (7), (B-2) and similarity transformation $\bar{{x}}_\delta = \mathfrak {R}\bar{{z}}_\delta$, yields the feedback control law of the system as:

$$\begin{aligned}&\bar{{u}}_\delta =- K (\xi _i ,\eta _i ) \bar{{x}}_\delta \nonumber \\&K (\xi _i ,\eta _i )= F [ \Gamma + P] \mathfrak {R}^{-1} \end{aligned}$$

(29)

where $F, P$, and $\Gamma$ are obtained using Eqs. (23), (24), and (28) as follows:

$$\begin{aligned} F&= (B_G ^{\prime }\hat{{B}}_G )^{-1}, P= B_G ^{\prime } (A_G -\hat{{A}}_G ),\nonumber \\ \Gamma&= B_G ^{\prime } (A_G -A_d). \end{aligned}$$

(30)