On the nonlinear stability of relative equilibria of the full spacecraft dynamics around an asteroid

Abstract

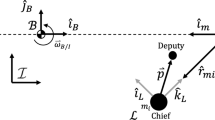
The full dynamics of a spacecraft around an asteroid, in which the gravitational orbit–attitude coupling is considered, has been shown to be of great value and interest. Nonlinear stability of the relative equilibria of the full dynamics of a rigid spacecraft around a uniformly rotating asteroid is studied with the method of geometric mechanics. The non-canonical Hamiltonian structure of the problem, i.e., Poisson tensor, Casimir functions and equations of motion, are given in the differential geometric method. A classical kind of relative equilibria of the spacecraft is determined from a global point of view, at which the mass center of the spacecraft is on a stationary orbit, and the attitude is constant with respect to the asteroid. The conditions of nonlinear stability of the relative equilibria are obtained with the energy-Casimir method through the semi-positive definiteness of the projected Hessian matrix of the variational Lagrangian. Finally, example asteroids with a wide range of parameters are considered, and the nonlinear stability criterion is calculated. However, it is found that the nonlinear stability condition cannot be satisfied by spacecraft with any mass distribution parameters. The nonlinear stability condition by us is only the sufficient condition, but not the necessary condition, for the nonlinear stability. It means that the energy-Casimir method cannot provide any information about nonlinear stability of the relative equilibria, and more powerful tools, which are the analogues of the Arnold’s theorem in the canonical Hamiltonian system with two degrees of freedom, are needed for a further investigation.

Appendix: Formulations of coefficients in characteristic equation

The explicit formulations of the coefficients in Eq. (43) are given as follows:

$$\begin{aligned}&A_{1} = 36\,\tau _{2} \,m^{2} \mu - 6\,\tau _{0} \,m^{2} \mu + 2\,R_{e}^{2} m^{2} \mu \nonumber \\&\quad +\,6\,m\mu \,I_{{yy}} - 12\,I_{{xx}} \,m\mu + 6\,m\mu I_{{zz}} - R_{e}^{5}.\end{aligned}$$

(48)

$$\begin{aligned}&A_{0} = 6\,\mu \,m\tau _{0} - 2\,R_{e}^{2} m\mu - 36\,\mu \,m\tau _{2} - \omega _{T}^{2} R_{e}^{5} m \nonumber \\&\quad -\,6\,\mu \,I_{{yy}} + 12\,I_{{xx}} \,\mu - 6\,\mu \,I_{{zz}}.\end{aligned}$$

(49)

$$\begin{aligned}&B_{2} = - 9mR_{e}^{3} \mu \,I_{{yy}} + 3\,m^{2} R_{e}^{3} \mu \,\tau _{0} - 3\,mR_{e}^{3} \mu \,I_{{zz}} \nonumber \\&\quad -\, 42\,m^{2} R_{e}^{3} \mu \,\tau _{2} - 2\,m^{2} R_{e}^{5} \mu - 12\,m^{2} R_{e}^{5} \mu \,\tau _{2} \nonumber \\&\quad +\, 12\,mR_{e}^{3} I_{{xx}} \,\mu - 2\,R_{e} ^{8}. \end{aligned}$$

(50)

$$\begin{aligned}&B_{1} = - 72\,m^{2} \mu ^{2} \tau _{2} \,I_{{xx}} + 2\,\mu \,mR_{e}^{5} - 18\,m^{3} \mu ^{2} \tau _{2} \,\tau _{0}\nonumber \\&\quad -\, 3\,mR_{e}^{3} \mu \,\tau _{0} + 12\,\mu \,mR_{e}^{5} \tau _{2} + 12\,m^{3} \mu ^{2} \tau _{2} \,R_{e}^{2} \nonumber \\&\quad +\, 9\,R_{e}^{3} \mu \,I_{{yy}} + 54\,m^{2} \mu ^{2} \tau _{2} \,I_{{yy}} - 12\,R_{e}^{3} I_{{xx}} \,\mu \nonumber \\&\quad +\, 3\,R_{e}^{3} \mu \,I_{{zz}} + 18\,m^{2} \mu ^{2} \tau _{2} \,I_{{zz}} + 108\,m^{3} \mu ^{2} \tau _{2}^{2} \nonumber \\&\quad -\, 2\,m\omega _{T}^{2}R_{e}^{8} + 42\,mR_{e}^{3} \mu \,\tau _{2}. \end{aligned}$$

(51)

$$\begin{aligned}&B_{0} = - 18\,m\mu ^{2} \tau _{2} \,I_{{zz}} + 72\,mI_{{xx}} \,\mu ^{2} \tau _{2} - 12\,m^{2} R_{e}^{2} \mu ^{2} \tau _{2} \nonumber \\&\quad +\, 12\,m^{2} R_{e}^{5} \omega _{T}^{2} \tau _{2} \,\mu + 18\,m^{2} \mu ^{2} \tau _{2} \,\tau _{0} \nonumber \\&\quad -\, 108\,m^{2} \mu ^{2} \tau _{2}^{2} - 54\,m\mu ^{2} \tau _{2} \,I_{{yy}}. \end{aligned}$$

(52)

$$\begin{aligned}&C_2 =-2\,R_e^8 \omega _T^2 I_{xx} \,I_{zz} -4\,mR_e^5 I_{xx} \,\mu -4\,R_e^8\nonumber \\&\quad +\,24\,R_e^3 I_{xx}^2 \mu -6\,R_e^3 I_{xx} \,\mu \,I_{yy} -18\,R_e^3 I_{xx} \,\mu \,I_{zz} \nonumber \\&\quad -\,60\,mR_e^3 I_{xx} \,\mu \,\tau _2 -2\,m\omega _T^2 I_{xx} \,R_e^{10} +6\,mR_e^5 I_{xx} \,\mu \,\tau _0\nonumber \\&\quad -\,12\,mR_e^5 I_{xx} \,\mu \,\tau _2 +18\,mR_e^3 I_{xx} \,\mu \,\tau _0.\end{aligned}$$

(53)

$$\begin{aligned}&C_1 =-2\,R_e^8 \omega _T^2 I_{xx} +4\,\mu \,mR_e^5 +12\,\mu \,mR_e^5 \tau _2 -24\,R_e^3 I_{xx} \,\mu \nonumber \\&\quad +\,18\,R_e^3 \mu \,I_{zz} -9\,mR_e^3 I_{xx} \,\mu \,\omega _T^2 I_{zz} \,\tau _0 \nonumber \\&\quad -\,9\,mI_{xx} \,\mu ^2\tau _0 \,I_{yy} -72\,mI_{xx}^2 \mu ^2\tau _2 +11\,mR_e^5 I_{xx} \,\mu \,\omega _T^2 I_{zz} \nonumber \\&\quad +\,6\,m^2R_e^5 \omega _T^2 \tau _2 \,\mu \,I_{xx} +3\,R_e^3 I_{xx} \,\mu \,\omega _T^2 I_{yy} \,I_{zz} \nonumber \\&\quad -\,6\,\mu \,mR_e^5 \tau _0 +3\,m^2R_e^5 \omega _T^2 \mu \,\tau _0 \,I_{xx} +2\,R_e^8 \omega _T^2 I_{zz} \nonumber \\&\quad +\,3\,mR_e^5 I_{xx} \,\mu \,\omega _T^2 I_{yy} +2\,m\omega _T^2 R_e^{10} +9\,R_e^3 I_{xx}\,\mu \,\omega _T^2 I_{zz}^2 \nonumber \\&\quad -\,2\,m^2\omega _T^4 I_{xx} \,R_e^{10} +2\,m^2I_{xx} \,\mu \,\omega _T^2 R_e^7 +18\,mI_{xx} \,\mu ^2\tau _2 \,I_{yy} \nonumber \\&\quad -\,72\,m^2\mu ^2\tau _2 \,\tau _0 \,I_{xx} -12\,R_e ^3I_{xx}^2 \mu \,\omega _T^2 I_{zz} \nonumber \\&\quad +\,108\,m^2I_{xx} \,\tau _2 ^2\mu ^2-6\,m^2R_e^2 I_{xx} \,\mu ^2\tau _0 +12\,m^2R_e^2 I_{xx}\,\mu ^2\tau _2 \nonumber \\&\quad -\,27\,mI_{xx} \,\mu ^2\tau _0 \,I_{zz} -12\,mR_e^5 I_{xx}^2 \mu \,\omega _T^2 \nonumber \\&\quad +\,9\,m^2\mu ^2\tau _0 ^2I_{xx} \!+\!54\,mI_{xx} \,\mu ^2\tau _2 \,I_{zz} \!+\!30\,mR_e^3 I_{xx} \,\mu \,\tau _2 \,\omega _T^2 I_{zz}\nonumber \\&\quad -\,18\,mR_e^3 \mu \,\tau _0 +36\,mI_{xx}^2 \mu ^2\tau _0 \nonumber \\&\quad +\,60\,mR_e^3 \mu \,\tau _2 +6\,R_e^3 \mu \,I_{yy}. \end{aligned}$$

(54)

$$\begin{aligned}&C_0 =-9\,m^2\mu ^2\tau _0^2 +2\,m^2\omega _T^4 R_e^{10} -11\,\mu \,mR_e^5 \omega _T^2 I_{zz} \nonumber \\&\quad -\,3\,\mu \,mR_e^5 \omega _T^2 I_{yy} +3\,R_e^3 I_{xx} \,\mu \,\omega _T^2 I_{yy} +21\,R_e^3 I_{xx} \,\mu \,\omega _T^2 I_{zz}\nonumber \\&\quad -\,3\,m^2R_e^5 \omega _T^2 \mu \,\tau _0 -3\,R_e^3 \mu \,\omega _T^2 I_{yy} \,I_{zz} +14\,\omega _T^2 R_e^5 mI_{xx} \,\mu \nonumber \\&\quad -\,6\,m^2R_e^5 \omega _T^2 \tau _2 \,\mu -9\,R_e^3 \mu \,\omega _T^2 I_{zz}^2\nonumber \\&\quad -\,18\,m\mu ^2\tau _2 \,I_{yy} +72\,mI_{xx} \,\tau _2 \,\mu ^2-36\,mI_{xx} \,\mu ^2\tau _0 \nonumber \\&\quad -\,54\,m\mu ^2\tau _2 \,I_{zz} +9\,m\mu ^2\tau _0 \,I_{yy} -108\,m^2\mu ^2\tau _2^2 \nonumber \\&\quad -\,2\,m^2\mu \,\omega _T^2 R_e^7 -12\,R_e ^3\omega _T^2 I_{xx}^2 \mu +72\,m^2\mu ^2\tau _2 \,\tau _0 \nonumber \\&\quad +\,6\,m^2R_e^2 \mu ^2\tau _0 -12\,m^2R_e^2 \mu ^2\tau _2 +27\,m\mu ^2\tau _0 \,I_{zz} \nonumber \\&\quad +\,9\,mR_e^3 \mu \,\omega _T^2 I_{zz} \,\tau _0 -9\,mR_e^3 \omega _T^2 I_{xx} \,\mu \,\tau _0 \nonumber \\&\quad -\,30\,mR_e^3 \mu \,\tau _2 \,\omega _T^2 I_{zz} +30\,mR_e^3 \omega _T^2 I_{xx} \,\tau _2 \,\mu . \end{aligned}$$

(55)

$$\begin{aligned}&D_2 =-2\,m-2\,I_{yy} -\omega _T^2 I_{yy} \,I_{zz} \,m-m^2\omega _T^2 I_{yy} \,R_e^2.\end{aligned}$$

(56)

$$\begin{aligned}&D_1 \!=\!2\!+\!\omega _T^2 I_{zz} \,m\!+\!m^2\omega _T^2 R_e^2 \!+\!\omega _T^2 I_{yy} \,I_{zz} \!-\!\omega _T^2 I_{yy} \,m.\end{aligned}$$

(57)

$$\begin{aligned}&D_0 =-\omega _T^2 I_{zz} +\omega _T^2 I_{yy}. \end{aligned}$$

(58)