Skip to main content
SpringerLink
Log in

Analysis of stability and Hopf bifurcation of delayed feedback spin stabilization of a rigid spacecraft

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

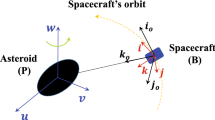
The stability and bifurcation of delayed feedback spin stabilization of a rigid spacecraft is investigated in this paper. The spin is stabilized about the principal axis of the intermediate moment of inertia using a simple delayed feedback control law. In particular, linear stability is analyzed via the exponential-polynomial characteristic equations and then the method of multiple scales is used to obtain the normal form of the Hopf bifurcation. Bifurcation diagrams and the dynamics of the delayed closed-loop system are verified using continuation software and with numerical simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

References

  1. Albu, I., Neamtu, M., Opris, D.: Dissipative mechanical systems with delay. Tensor 67, 1–27 (2006)

    MathSciNet  MATH  Google Scholar 

  2. Albu, I., Neamtu, M., Opris, D.: The dynamical rigid body with memory. In: Balkan Society of Geometers (BSG) Proceedings of International Conference of Differential Geometry Dynamical Systems (DGDS), October 5–7, 2007, vol. 15, pp. 1–10. Geometry Balkan Press, Bucharest (2008)

    Google Scholar 

  3. Ramnath, R.V.: Multiple Scales Theory and Aerospace Applications. AIAA, Reston (2010)

    Book  Google Scholar 

  4. Tao, Y.C., Ramnath, R.V.: Satellite Attitude Prediction by Multiple Time Scales Method. The Charles Stark Draper Laboratory, Cambridge (1975)

    Google Scholar 

  5. Alfriend, K.T.: Magnetic attitude control system for dual-spin satellites. AIAA J. 13(6), 817–822 (1975)

    Article  MATH  Google Scholar 

  6. Gebman, J.R., Mingori, D.L.: Perturbation solution for the flat spin recovery of a dual-spin spacecraft. AIAA J. 14(7), 859–867 (1976)

    Article  Google Scholar 

  7. Chunodkar, A., Akella, M.: Attitude stabilization with unknown bounded delay in feedback control implementation. J. Guid. Control Dyn. 34(2), 533–542 (2011)

    Article  Google Scholar 

  8. Samiei, E., Nazari, M., Butcher, E., Schaub, H.: Delayed feedback control of rigid body attitude using neural networks and Lyapunov–Krasovskii functionals. In: AAS/AIAA Spaceflight Mechanics Meeting, Charleston, SC (2012). Paper No. 12-168

    Google Scholar 

  9. Nazari, M., Butcher, E., Schaub, H.: Spacecraft Attitude Stabilization using Nonlinear Delayed Multi-Actuator Control and Inverse Dynamics. J. Guid. Control Dyn. (2013). doi:10.2514/1.58249

    MATH  Google Scholar 

  10. Nayfeh, A.: Method of Normal Forms. Wiley, New York (1993)

    MATH  Google Scholar 

  11. Bambusi, D.: Galerkin averaging method and Poincaré normal form for some quasilinear PDEs. Ann. Sc. Norm. Super. Pisa, Cl. Sci. 4(5), 669–702 (2005)

    MathSciNet  MATH  Google Scholar 

  12. Butcher, E.: Normal forms for high co-dimension bifurcations of nonlinear time-periodic systems with nonsemisimple eigenvalues. Nonlinear Dyn. 30, 29–53 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  13. Nayfeh, A.: Order reduction of retarded nonlinear systems—the method of multiple scales versus center-manifold reduction. Nonlinear Dyn. 51, 483–500 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  14. Xu, J., Lu, Q.: Hopf bifurcation in a time-delayed lienard equation. Int. J. Bifurc. Chaos Appl. Sci. Eng. 9(5), 939–951 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  15. Faria, T.: Normal forms and Hopf bifurcation for partial differential equations with delays. Trans. Am. Math. Soc. 352(5), 2217–2238 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  16. Das, S., Chatterjee, A.: Multiple scales without center manifold reductions for delay differential equations near Hopf bifurcations. Nonlinear Dyn. 30, 323–335 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  17. Kielhöfer, H.: Bifurcation Theory: an Introduction with Applications to Partial Differential Equations. Springer, New York (2004)

    Google Scholar 

  18. Doedel, E., Champneys, A.T.F., Kuznetsov, Y., Oldeman, B., Paffenroth, R., Sandstede, B., Wang, X., Zhang, C.: AUTO-07p: Continuation and Bifurcation Software for Ordinary Differential Equations. Concordia University Montreal, Canada (2007)

    Google Scholar 

  19. Insperger, T., Stépán, G.: Semi-Discretization for Time-Delay Systems: Stability and Engineering Applications. Springer, New York (2011)

    Book  Google Scholar 

  20. Bers, L., John, F., Schechter, M.: Partial differential equations. In: Lectures in Applied Mathematics, vol. 3A, pp. 1–343. Wiley, New York (1964)

    Google Scholar 

  21. Nayfeh, A.: Problems in Perturbation. Wiley, New York (1985)

    MATH  Google Scholar 

  22. Schaub, H., Junkins, J.: Analytical Mechanics of Space Systems. AIAA, Reston (2009)

    MATH  Google Scholar 

  23. Engelborghs, K., Luzyanina, T., Samaey, G.: DDE-BIFTOOL v. 2.00: A Matlab Package for Bifurcation Analysis of Delay Differential Equations. Department of Computer Science. K.U. Leuven, Technical Report TW-330, Leuven, Belgium (2001)

  24. Engelborghs, K., Luzyanina, T., Roose, D.: Numerical bifurcation analysis of delay differential equations using DDE-BIFTOOL. ACM Trans. Math. Softw. 28(1), 1–21 (2002)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgement

Financial support of from the National Science Foundation under Grant No. CMMI-1131646 is gratefully acknowledged. The authors would also like to thank Dr. Young S. Lee for his valuable help and support.

Author information

Authors and Affiliations

  1. Department of Mechanical and Aerospace Engineering, New Mexico State University, Las Cruces, NM, 88003, USA

    Morad Nazari & Eric A. Butcher

Authors
  1. Morad Nazari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Eric A. Butcher
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Morad Nazari.

Appendix

Appendix

1.1 Critical frequency of the characteristic equation in Sect. 3.1

Substituting for k p from Eq. (8) into Eq. (10a) on the stability boundary, the term \(\kappa_{c}^{2}\cos 2\gamma_{c} \tau\) appears which, using trigonometric identities, can be expressed as

$$\begin{aligned} \kappa_c^2\cos 2 \gamma_c \tau =&\kappa_c^2\bigl(1-2 \sin^2\gamma_c \tau\bigr) \\ =&\kappa_c^2-2(\kappa_c\sin \gamma_c\tau)^2. \end{aligned}$$
(A.1)

Solving Eq. (10b) for κ c gives

$$\begin{aligned} \kappa_c=\frac{J_2+J_3}{2}\frac{\gamma_c}{\sin\gamma_c\tau}. \end{aligned}$$
(A.2)

Substituting Eq. (A.2) into Eq. (A.1), one can obtain

$$\begin{aligned} \kappa_c^2\cos2 \gamma_c\tau =&\frac{(J_2+J_3)^2}{4}\frac{\gamma_c^2}{\sin^2\gamma_c\tau}-2 \frac{(J_2+J_3)^2}{4}\gamma_c^2 \\ =&\frac{(J_2+J_3)^2}{4}\gamma_c^2 \biggl(\frac{1}{ \sin^2\gamma_c\tau}-2 \biggr). \end{aligned}$$
(A.3)

Substituting Eqs. (A.2) and (A.3) into Eq. (10a), it becomes

$$\begin{aligned} &-\gamma_c^2+\gamma_c^2 \biggl(\frac{J_2+J_3}{J_2J_3} \biggr)\frac{J_2+J_3}{2} \\ &\qquad{}+\frac{(J_2+J_3)^2}{4J_2J_3}\gamma_c^2 \biggl(\frac{1}{ \sin^2\gamma_c\tau}-2 \biggr) \\ &\quad{}=\frac{(J_3-J_1)}{(J_1-J_2)}{J_2J_3}\varOmega_1^2, \end{aligned}$$
(A.4)

where Eq. (8) is used to substitute for α, k p , and k d in terms of κ and the parameters of the system. Therefore, the critical frequency corresponding to κ c can be obtained via

$$\begin{aligned} \gamma_c =&\varOmega_1\sqrt{\frac{(J_3-J_1)(J_1-J_2)}{-1+\frac{1}{2}(J_2+J_3)^2 [1+\frac{1}{2} (\frac{1}{\sin^2\gamma_c\tau}-2 ) ]}} \\ =&\varOmega_1\sqrt{\frac{(J_1-J_3)(J_1-J_2)}{1-\frac{(J_2+J_3)^2}{4\sin^2\gamma_c\tau}}}, \end{aligned}$$
(A.5)

or, after using Eq. (A.2), the critical frequency can be expressed in terms of κ c as

$$\begin{aligned} \gamma_c^2=\frac{1}{J_2J_3} \bigl[\kappa_c^2+\varOmega_1^2(J_3-J_1) (J_2-J_1) \bigr]. \end{aligned}$$
(A.6)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Nazari, M., Butcher, E.A. Analysis of stability and Hopf bifurcation of delayed feedback spin stabilization of a rigid spacecraft. Nonlinear Dyn 74, 801–817 (2013). https://doi.org/10.1007/s11071-013-1006-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-013-1006-5

Keywords

Search

Navigation