Nonlinear vibration of viscoelastic sandwich plates under narrow-band random excitations

Abstract

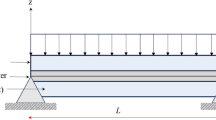
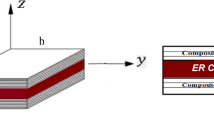
The effect of the narrow-band random excitation on the non-linear response of sandwich plates with an incompressible viscoelastic core is investigated. To model the core, both the transverse shear strains and rotations are assumed to be moderate and the displacement field in the thickness direction is assumed to be linear for the in-plane components and quadratic for the out-of-plane components. In connection to the moderate shear strains considered for the core, a non-linear single-integral viscoelastic model is also used for constitutive modeling of the core. The fifth-order perturbation method is used together with the Galerkin method to transform the nine partial differential equations to a single ordinary integro-differential equation. Converting the lower-order viscoelastic integral term to the differential form, the fifth-order method of multiple scale is applied together with the method of reconstitution to obtain the stochastic phase-amplitude equations. The Fokker–Planck–Kolmogorov equation corresponding to these equations is then solved by the finite difference method, to determine the probability density of the response. The variation of root mean square and marginal probability density of the response amplitude with excitation deterministic frequency and magnitudes are investigated and the bimodal distribution is recognized in narrow ranges of excitation frequency and magnitude.

Appendices

Appendix A: Derivation of kinematic relations

Consider the Green strain tensor written in terms of the linear strain tensor, e, and the linear rotation tensor, Ω, as

(49)

where e and Ω are related to the displacement gradient matrix (∂ U/∂ X) of the core as

(50)

with U being the displacement vector and $\mathbf{X} = (x_{1},x_{2},x_{3}^{(c)})$ is the position vector of a particle at its un-deformed state. For bending deformation of shell type structure, the following ordering is commonly used based on the assumption of moderate transverse rotations:

$$ \varOmega_{\alpha3} = O(\theta), \qquad \varOmega_{\alpha\beta} = O\bigl( \theta^{2}\bigr), $$

(51)

where α,β=1,2 in Eqs. (51) and all the subsequent formulations. θ ² is also a small number compared to unity [33, 34]. The order of magnitude of the linear strain tensor components are also assumed as

$$ e_{\alpha3} = O(\theta),\quad e_{\alpha\beta} = O\bigl(\theta^{2} \bigr),\quad e_{33} = O\bigl(\theta^{2}\bigr). $$

(52)

This is the same as the assumption made in Refs. [35–37] except that the transverse shear strains are assumed to be moderate here due to the constraint of the core between stiff layers. Using Eqs. (51) and (52) in Eq. (49), neglecting the terms of order θ ⁴ and higher [37, 38], and using Eqs. (50) yield [35–37]

$$\begin{aligned} &{E_{\alpha\beta} = \frac{1}{2} ( U_{\alpha,\beta} + U_{\beta,\alpha } + U_{3,\alpha} U_{3,\beta} ),} \\&{E_{\alpha3} = \frac{1}{2} \biggl( U_{3,\alpha} + U_{\alpha,3}} \\ \\&{\hphantom{E_{\alpha3} =}{} + \sum_{i = 1,2} U_{i,\alpha} U_{i,3} + U_{3,3}U_{3,\alpha} \biggr),} \\&{E_{33} = U_{3,3} + \frac{1}{2}\sum _{i = 1,2} U_{i,3} ^{2},} \end{aligned}$$

(53)

where ()_,i denotes the partial differentiation with respect to $x_{i}^{(c)}$. Equation (53) is the same as the equation given in Ref. [38] for shell-type structures based on the assumption of moderate transverse rotations. Thus the assumption of moderate shear strain does not affect the strain-displacement relations. Next, substituting the assumed displacement distribution (i.e., Eqs. (1)) into Eq. (49), and assuming that $\mathop{u}\limits^{1}\!{}_{3,\alpha} ^{(c)}$, $\mathop{u}\limits ^{2}\!{}_{3,\alpha} ^{(c)}$ and $\mathop{u}\limits^{2}\!{}_{3}^{(c)}$ are all of order θ ³, the final form of strain-displacement relations given in Eqs. (2) and (3) will be obtained. It must be emphasized that the last assumption, on the order of magnitudes of $\mathop{u}\limits^{1}\!{}_{3,\alpha} ^{(c)}$, $\mathop{u}\limits ^{2}\!{}_{3,\alpha} ^{(c)}$ and $\mathop{u}\limits^{2}\!{}_{3}^{(c)}$, is not in contrast to the initial assumption made on the linear strain and rotation components in Eqs. (51) and (52). This assumption also seems to be physically reasonable, since the through-the-thickness deformation of the especially incompressible core is expected to be much lower than the overall transverse displacement.

Appendix B: Derivation of incompressibility constraints

Expanding |2E+I|=1 yields [39, 40]

$$\begin{aligned} &{\operatorname{tr} \mathbf{E} + ( \operatorname{tr} \mathbf{E} )^{2} - \operatorname{tr} \mathbf{E}^{2}} \\&{\quad {} + \frac{2}{3} \bigl[ 2 \operatorname{tr} \mathbf{E}^{3} - 3\operatorname{tr} \mathbf{E} \operatorname{tr} \mathbf{E}^{2} + ( \operatorname{tr} \mathbf{E} )^{3} \bigr] = 0,} \end{aligned}$$

(54)

where $\operatorname{tr}$ denotes trace of a matrix. Retaining the terms of order θ ³ and lower in Eq. (54), the simplified form of the incompressibility constraint is obtained as

$$ 2\operatorname{tr} \mathbf{E} - 4\sum_{\alpha= 1,2} E_{\alpha3}^{2} + O\bigl(\bar{\varepsilon} ^{4}\bigr) = 0, $$

(55)

which, upon substituting for components of E from Eq. (3), and setting the coefficients of different powers of $x_{3}^{(c)}$ equal to 0 yields

$$ \begin{array}{@{}l} \displaystyle \mathop{u}\limits ^{1}\!{}_{3}^{(c)} + \sum _{i = 1,2} \mathop{u}\limits ^{0}\!{}_{i,i}^{(c)} - \sum _{i = 1,2} \mathop{u}\limits ^{1}\!{}_{i}^{(c)} \mathop{u}\limits ^{0}\!{}_{3,i}^{(c)} = 0,\\ \displaystyle 2\mathop{u}\limits ^{2}\!{}_{3}^{(c)} + \mathop{u}\limits ^{1}\!{}_{i,i}^{(c)} = 0. \end{array} $$

(56)

Appendix C: Derivation of constitutive equation

Based on the modification made by Pipkin [40] in the Green-Rivlin model for an isotropic incompressible viscoelastic material, and using the simplification procedure proposed by Stafford [19] and Nambudiripad and Neis [20], the following single integral constitutive relation can be obtained from the three-integral Green-Rivlin model:

$$\begin{aligned} \mathbf{S}(\mathbf{X},t) =& - p(\mathbf{X},t)\mathbf {C}^{ - 1}( \mathbf{X},t) \\&{} + \int_{ - \infty} ^{t} \biggl\{ k_{1}(t - \tau)\dot{\mathbf{E}}(\mathbf {X},\tau) \\&{} + k_{2}(t - \tau )\frac{d}{d\tau} \bigl[ \mathbf{E}(\mathbf{X},\tau)^{2} \bigr] \\&{}+ k_{3}(t - \tau )\frac{d}{d\tau} \bigl[ \mathbf{E}(\mathbf{X}, \tau)^{3} \bigr] \\&{} + k_{4}(t - \tau)\frac{d}{d\tau} \bigl[ \mathbf{E}(\mathbf{X},\tau)\operatorname{tr} \bigl( \mathbf {E}(\mathbf{X}, \tau)^{2} \bigr) \bigr] \biggr\}\,d\tau \\ \end{aligned}$$

(57)

where S is the second Piola–Kirchhoff stress tensor and dot represents differentiation with respect to time. Also, p is an unknown hydrostatic pressure, which is the result of the volume-preserving constraint of an incompressible material and C is the Cauchy–Green strain tensor, which is related to the Green strain tensor by C=(2E+I) with I being the identity matrix of dimension 3. The temporal functions k _i ’s, (i=1,…,4) in Eq. (57) are also the stress–relaxation functions that are generally determined from experiment. In Eq. (57), C ⁻¹ can be defined in terms of E by the Taylor expansion of [I−C ⁻¹] around E as [40]

$$\begin{aligned} &{\bigl[ \mathbf{I} - \mathbf{C}^{ - 1} \bigr] = 2\mathbf{E} ( \mathbf{I} + 2\mathbf{E} )^{ - 1} = 2\mathbf{E} - 4\mathbf{E}^{2} + 8 \mathbf{E}^{3} + \cdots.} \\ \end{aligned}$$

(58)

The reason for retaining up to third-order terms in Eq. (58) is that E is assumed to be generally of order θ. Therefore, some higher order terms still exist in Eq. (58) that will be discarded in the final constitutive equations.

Substituting Eq. (58) into Eq. (57), assuming that the medium is in its un-deformed state for t=(−∞,0), and the strain history is differentiable for t>0, yield [41, 42]

$$\begin{aligned} \mathbf{S}(\mathbf{X},t) =& - p(\mathbf{X},t)\mathbf{I} + \bigl[ 2p( \mathbf{X},t) + k_{1}(0) \bigr]\mathbf{E}(\mathbf{X},\tau) \\&{} + \bigl[ - 4p(\mathbf {X},t) + k_{2}(0) \bigr]\mathbf{E}(\mathbf{X}, \tau)^{2} \\&{} + \bigl[ 8p(\mathbf{X},t) + k_{3}(0) \bigr]\mathbf{E}(\mathbf{X}, \tau)^{3} \\&{} + k_{4}(0)\mathbf{E}(\mathbf {X},\tau ) \operatorname{tr} \bigl( \mathbf{E}(\mathbf{X},\tau)^{2} \bigr) \\&{} + \int _{0}^{t} \biggl\{ \frac{dk_{1}(t - \tau)}{d(t - \tau)}\mathbf{E}( \mathbf{X},\tau) \\&{}+ \frac{dk_{2}(t - \tau)}{d(t - \tau)}\mathbf{E}(\mathbf{X},\tau)^{2} \\&{} + \frac{dk_{3}(t - \tau)}{d(t - \tau )}\mathbf{E}(\mathbf{X},\tau)^{3} \\&{} + \frac{dk_{4}(t - \tau)}{d(t - \tau )} \mathbf{E}(\mathbf{X},\tau)\operatorname{tr} \bigl( \mathbf{E}(\mathbf {X}, \tau)^{2} \bigr) \biggr\}\,d\tau. \\ \end{aligned}$$

(59)

The final step to completely define the constitutive equation of the core is to determine k _i ’s. These functions must in fact be obtained from experiment. However, in the present study, for the purpose of qualitative investigation, they are assumed to be in the form of the Standard Linear Solid (SLS) model’s stress relaxation function as [43]

$$ k_{i}(t) = k_{i0} \bigl[ ( 1 - \gamma )e^{ - t/t_{R}} + \gamma \bigr],\quad 0 < \gamma< 1, $$

(60)

where t _R is the stress relaxation time and k _i0 and γ are related to the initial modulus, and the residual to initial modulus ratio, respectively. Moreover, based on the fact that the behavior of viscoelastic materials is elastic at limits of time [39], k _i0’s are chosen in a way that the initial instantaneous and the steady-state response of the material conform to the Mooney–Rivlin model. For this purpose, the constitutive equation of Mooney–Rivlin material, given in Ref. [43], is written in terms of the second Piola–Kirchhoff stress tensor, S and E, as

$$\begin{aligned} \mathbf{S} =& {-} \mathop{p}\limits ^{ *} [ 2\mathbf{E} + \mathbf{I} ]^{ - 1} + c_{0} \bigl[ 1 + 2\mu \bigl(\operatorname{tr}(\mathbf{E}) + 1 \bigr) \bigr]\mathbf{I} \\&{} - 2\mu \mathbf{E}, \end{aligned}$$

(61)

where c ₀ and μ are the Mooney–Rivlin material’s constants. The scalar function, $\mathop{p}\limits^{ *}$, has also arisen from the incompressibility constraint and is defined by the relation $\mathop{p}\limits^{ *} = p + ( 1 + 2\mu+ 2\mu \operatorname{tr}(\mathbf{E}) )c_{0}$. Using Eq. (58) and the fact that $\operatorname{tr}(\mathbf{E})$ is of order θ ² (see Eq. (55)), Eq. (61) will be reduced to the following equation by discarding the terms of higher order than θ ³:

$$\begin{aligned} \mathbf{S} =& {-} \mathop{p}\limits \mathbf{I} + \bigl[ 2p + 2 ( 1 + \mu )c_{0} \bigr] \mathbf{E} \\&{} - 4 \bigl[ p + (1 + 2\mu)c_{0} \bigr]\mathbf{E}^{2} \\&{} + 8 \bigl[ p + (1 + 2\mu)c_{0} \bigr]\mathbf{E}^{3} + 4c_{0}\mu\operatorname {tr}(\mathbf{E})\mathbf{E}. \end{aligned}$$

(62)

Comparing Eq. (62) with Eq. (59) and using Eq. (60), k _i0’s will be determined as

$$ \begin{array}{@{}l} k_{10} = 2 ( 1 + \mu )c_{0},\qquad k_{20} = - 4(1 + 2 \mu)c_{0},\\ k_{30} = 8(1 + 2\mu)c_{0},\qquad k_{40} = 4c_{0}\mu. \end{array} $$

(63)

Using Eqs. (59)–(61) and (63), and neglecting the terms of higher order than θ ³, the final form of the constitutive equation given in Eqs. (6) and (7) can be obtained.

Appendix D: Stress resultants in terms of strain components

$$ \mathop{\mathbf{N}}\limits ^{j}{}^{(c)} = \mathop{\mathbf{N}} \limits^{j}{}_{e}^{(c)} - \frac{(1 - \gamma )}{t_{R}}\int_{0}^{t} \mathop{\mathbf{N}} \limits^{j}{}_{e}^{(c)}( \tau ) e^{ - (t - \tau )/t_{R}}d\tau $$

(64)

where,

(65)

where in Eqs. (65), j=0,2 and $\tilde{k}_{10} = h_{c}, \tilde{k}_{20} = \tilde{k}_{12} = h_{c}^{3}/12$, and $\tilde{k}_{22} = h_{c}^{5}/80$.