1 Introduction

Spatial soliton is a stable self-trapped wave packet propagating in a nonlinear (NL) medium, in which diffraction is exactly balanced by the nonlinearity [1]. One of the most often used models to describe two-dimensional (2D) optical spatial solitons propagating in Kerr media is the nonlinear Schrödinger (NLS) equation [1, 2]. Spatial solitons have been identified in many physical systems and can self-trap in two transverse dimensions [2]; however, their stability is still an open problem. It can be improved, for example by employing soliton management techniques [3] or by including nonlocality into the analysis. We have recently considered two types of strongly nonlocal solitons with azimuthal symmetry. The first one corresponds to solitons with maximum intensity at the center, surrounded by dark rings [4, 5] and the second to solitons with zero intensity in the center, surrounded by bright rings [6]. In both cases the solitons have been shown to be unstable in Kerr media with constant diffraction and nonlinearity coefficients [7]. Depending on whether their power is above or below a critical point, Kerr solitons either focus to a zero radius (i.e., undergo catastrophic collapse) or diffract and broaden [8]. Saturation may suppress this collapse, but the rings still suffer from azimuthal instabilities, which grow with propagation. A bright ring, however, can self-trap in a stable fashion in a saturable medium [9] if it is a component of a vector soliton [10]. Another family of ring solitons comprises the necklace beams [11]—the beams that become stable by having the intensity azimuthally modulated and resemble pearls in a necklace. The construction of various types of robust soliton clusters in both 2D and 3D physical settings has been considered by a number of authors [12–16]. Recent review work [17] lists a variety of exact solutions of the (2+1)-dimensional nonlinear Schrodinger equation with the trapping potential, including soliton clusters having the special form of “dromion lattices”.

Spatial solitons can also be divided into scalar solitons (one-component) and vector solitons (multicomponent), according to the number of field components [18]. An important prerequisite for the generation of vector solitons is the absence of interference between components. In general, there exist many ways to generate vector solitons. The first, suggested by Manakov [19], consist in considering two orthogonally polarized optical field components in a NL Kerr medium, in which self-phase modulation (SPM) is equal to cross-phase modulation (XPM). Another approach is realized by considering two beams of different wavelengths in the case of quadratic solitons [20]. Finally, vector solitons can be formed using mutually incoherent beams which consist of two-component azimuthons [17]. In NL optics, the XPM-mediated interaction between mutually incoherent or orthogonally polarized waves leads to the formation of bound states, also known as vector solitons. Such sets of vector spatial solitons include vortices [21], dipoles [17], and multipole-mode solitons [22]. Since azimuthons constitute a link between vortex solitons and other types of NL localized excitations, it is natural to seek localized coupled bound states with azimuthal modulation and form directly higher-order vector solitons.

In our previous works [16], we report the localized dipole solitons which exhibit symmetric shapes, using the Hirota method. However, Hirota’s method is mathematically complex; it is hard to follow its physical consequences and it rarely leads to closed sets of modes. In this paper, we introduce again the concept of azimuthal modulation but in a simpler setting, in which two interacting components of the spatially localized resonance solitons exist in the same model with self-focusing and self-defocusing NL coefficients and nontrivial special trapping potential. Specifically, we demonstrate how to realize resonance solitons in the physical system consisting of two-component solitons in 2D NL Kerr medium, by selecting appropriately the self-consistency and resonance conditions. It is noted that the intensity of resonance solitons does not change with propagation distance; they display the characteristics of an ideal information carrier. As far as we know, no other reports exist following this line of inquiry.

The paper is organized as follows. In Sect. 2, we describe the model that governs azimuthally modulated dynamics of a binary beam mixture, by properly selecting the self-consistency conditions. We also introduce a special trapping potential, to help us form the resonance solitons. The lowest-order scalar resonance soliton with a single component and different vector resonance soliton clusters, including vortex and necklace solitons, are described in Sect. 3. The azimuthon-azimuthon bound states are also discussed in this section. The dynamic instabilities of the bound states of fundamental and other soliton states are studied numerically in Sect. 4. Finally, Sect. 5 concludes the paper.

2 The model and resonance solitons

To construct scalar and vector solitons consisting of N mutually incoherent optical components propagating in a self-focusing and self-defocusing Kerr NL medium, we utilize a system of coupled (2+1)D NLS equations for the evolution of the slowly varying field envelopes E j (z,r,φ) (j=1,2,…,N). Here z is the propagation coordinate, and r and φ are the polar coordinates in the transverse plane. The generalized NLS equations are of the following dimensionless form [16, 23]:

$$ i\frac{\partial E_{j}}{\partial z} = - \frac{1}{2}\nabla_{ \bot} ^{2}E_{j} + g ( z,r )\sum_{j = 1}^{N} \vert E_{j} \vert ^{2} E_{j} + V ( z,r )E_{j}, $$
(1)

where all the SPM and XPM contributions are taken to be equal. The factor g(z,r) stands for the variable nonlinearity coefficient; the diffraction coefficient in the second term in Eq. (1) has been normalized. Here, \(\nabla_{ \bot} ^{2} = \frac {\partial^{2}}{\partial r^{2}} + \frac{1}{r}\frac{\partial}{\partial r} + \frac{1}{r^{2}}\frac{\partial ^{2}}{\partial\varphi ^{2}}\) is the transverse 2D Laplacian with the transverse radial coordinate \(r = \sqrt{x^{2} + y^{2}}\); φ is the azimuthal angle and V(z,r) is a special trapping potential, to be determined.

We presume the solutions of Eq. (1) in the form E j (r,φ,z)=u(z,r)Φ j (φ). Substituting this into Eq. (1), we find

(2)

We assume that Eq. (2) satisfies the self-consistency condition \(\sum _{j = 1}^{N} | \varPhi _{j}( \varphi)|^{2} = 1\), allowing the separation of variables in Eq. (2). This leads to the following two equations:

$$ \frac{\partial^{2}\varPhi_{j}}{\partial\varphi^{2}} + m^{2}\varPhi_{j} = 0, $$
(3a)
(3b)

where m is the separation constant, also known as the topological charge (TC); it is assumed to be an integer [4, 5, 24]. Obvious solutions to Eq. (3a) are the functions Φ j (φ)=A j cosmφ+B j sinmφ, with the complex coefficients A j and B j obeying conditions \(\sum_{j = 1}^{N} \operatorname{Re}( A_{j}B_{j}^{ *}) = 0\) and \(\sum_{j = 1}^{N}| A_{j} |^{2} = \sum_{j = 1}^{N} | B_{j} |^{2} = 1\). These equations define analytical solutions of Eq. (1) for any integer N. In the particular case N=1, they describe a scalar soliton with arbitrary TC m, A=1, and B=i. In general, N is an integer larger than 1, so the system describes vector solitons with azimuthal modulation. In this paper, we focus on the simplest solutions of the two-component (N=2) case and choose the corresponding coefficients as follows: A 1=(1+q)−1/2, B 1=iqA 1, A 2=qA 1, B 2=iA 1, where the parameter q, 0≤q≤1, determines the modulation depth of the beam. For an arbitrary q, representing the incoherent superposition of two components, we obtain two-component vector solitons.

Let us now deal with Eq. (3b). Our aim is to transform Eq. (3b) into the standard NLS equation [25, 26] with constant nonlinearity coefficient

$$ \mu U + \frac{1}{2}\frac{\partial^{2}U}{\partial R^{2}} + GU^{3} = 0, $$
(4)

where U=U(R) depends only on R≡R(z,r), both of them real functions. Here, μ denotes the eigenvalue of the NLS equation, and G is a constant nonlinearity coefficient; the choices G=1 and G=−1 lead to the bright and dark soliton solutions, respectively. Next, we construct the bright soliton solution of Eq. (4), for the case of negative eigenvalue μ<0 and G=1,

$$ U ( R ) = \sqrt{ - 2\mu} \operatorname{sech} ( \sqrt{ - 2\mu} R ), $$
(5A)

and for the case of positive eigenvalue μ>0 and G=−1, the dark soliton solution,

$$ U ( R ) = \sqrt{\mu} \tanh ( \sqrt{\mu} R ). $$
(5B)

To connect solutions of Eq. (3b) with those of Eq. (4), we use the following similarity transformation:

$$ u ( z,r ) = \rho ( z,r ) U \bigl[ R ( z,r ) \bigr]e^{i\varOmega ( z,r )}, $$
(6)

where the amplitude ρ(z,r) (ρ is positive) and the phase Ω(z,r) are real functions of z and r. This kind of transformation has been studied for the generalized NLS equations in various contexts [25–27]. It should be emphasized that we require U(R) to satisfy Eq. (4) and u(z,r) to be a solution of Eq. (3b). The substitution of Eq. (6) into Eq. (3b) leads to Eq. (4) and in addition one obtains a system of partial differential equations to solve:

$$ R_{z} + R_{r}\varOmega_{r} = 0, $$
(7A)
$$ r \bigl( \rho^{2}\varOmega_{r} \bigr)_{r} + \rho^{2}\varOmega_{r} + 2r\rho\rho_{z} = 0, $$
(7B)
$$ - g\rho^{2} - GR_{r}^{2} = 0, $$
(7C)
$$ r \bigl( \rho^{2}R_{r} \bigr)_{r} + \rho^{2}R_{r} = 0, $$
(7D)
$$ \frac{\rho_{rr}}{\rho} - 2\varOmega_{z} - \varOmega_{r}^{2} - \frac {m^{2}}{r^{2}} + \frac{\rho _{r}}{r\rho} - 2V - 2\mu R_{r}^{2} = 0, $$
(7E)

where the subscripts r and z mean partial derivatives of the function with respect to r and z. To find exact solutions of Eqs. (7A)–(7E), we introduce another self-similar transformation [4, 5] and a few auxiliary functions:

$$ \rho ( z,r ) = \frac{k}{w ( z )}F ( \theta ),\qquad\varOmega ( z,r ) = a ( z )r^{2} + b ( z ), $$
(8)

where k is the normalization constant. Here, w(z) is the beam width, θ(z,r) is the similarity variable to be determined, a(z) is the wave front curvature, and b(z) represents the phase offset. These variables are all allowed to vary with propagation distance z. Inserting Eqs. (8) into Eqs. (7A)–(7E), after some algebra one obtains the following expressions for \(\theta ( z,r ) = \frac {r^{2}}{w^{2} ( z )}\), the wave front curvature \(c ( z ) = \frac{1}{2w}\frac{dw}{dz}\), and

$$ R ( z,r ) = \int_{0}^{\frac{r}{w}} \frac{1}{tF^{2} ( t )} \,dt, $$
(9A)
$$ g ( z,r ) = - \frac{GR_{r}^{2}}{\rho^{2}}. $$
(9B)

The amplitude ρ(z,r) is found from Eq. (7E), which is transformed into the following NL differential equation for F(θ)

(10)

We choose the special trapping potential as follows:

$$ V ( z,r ) = s^{2}r^{2} - \mu R_{r}^{2}, $$
(11)

where s is a positive constant, and after a variable transformation \(F( \theta) = \theta^{ - \frac{1}{2}}f( \theta)\), from Eq. (10) we arrive at

$$ \frac{d^{2}f}{d\theta^{2}} + \biggl[ - \frac{1}{4} + \frac{n}{\theta} + \frac{1 - m^{2}}{4\theta ^{2}} \biggr]f = 0, $$
(12A)

with

$$ - \frac{m + 1}{2} - \frac{w^{2}}{2}b_{z} = n, $$
(12B)

and

$$ \frac{1}{2w^{2}} - \frac{w}{2}\frac{d^{2}w}{dz^{2}} - s^{2}w^{2} = 0. $$
(12C)

Here, n (=0,1,2,…) is a non-negative integer. The differential equation (12A) is known as the Whittaker differential equation and its solutions are the Whittaker functions [28], namely f(θ)=W nm (θ) with

(13)

where Γ is the Gamma function. Taking w(z)| z=0=w 0 and \(\frac{dw( z )}{dz}|_{z = 0} = 0\), where the subscript 0 denotes the value of the corresponding quantity at z=0, and integrating Eq. (12C) yields [4, 5]

$$ w^{2} = w_{0}^{2} \bigl[ 1 + ( \lambda- 1 ) \sin^{2} \bigl( 2sw_{0}^{2}z \bigr) \bigr], $$
(14A)

where \(\lambda= \frac{1}{2s^{2}w_{0}^{4}}\). Hence, from Eqs. (14A), (12B) and from the definition of \(a( z ) = \frac{1}{2w}\frac{dw}{dz}\), we obtain

$$ b ( z ) = b_{0} - \frac{ ( 2n + m + 1 )\tan^{ - 1} [ \sqrt{\lambda} \tan ( 2sw_{0}^{2}z ) ]}{2s\sqrt{\lambda} w_{0}^{4}}, $$
(14B)
$$ a ( z ) = \frac{sw_{0}^{2} ( \lambda- 1 )\sin ( 4sw_{0}^{2}z )}{1 + \lambda- ( \lambda- 1 )\cos ( 4sw_{0}^{2}z )}. $$
(14C)

Collecting all these partial solutions together, we finally obtain the analytical solution of Eq. (1):

$$ \begin{array}[b]{@{}lll} E_{j} ( z,r,\varphi ) &=& \displaystyle\frac{k ( A_{j}\cos m\varphi+ B_{j}\sin m\varphi )}{r}W_{nm} \biggl( \frac{r^{2}}{w^{2}} \biggr)\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\[4mm] &&{}\times U \bigl[ R ( z,r ) \bigr]e^{i [ a ( z )r^{2} + b ( z ) ]}, \end{array} $$
(15A)

where j=1,2. Here, w(z), a(z),b(z), U(R), R(z,r), W nm (r 2/w 2) are determined by Eqs. (14A)–(14C), (5A)–(5B), (9A), (13), and \(k = \sqrt{\frac{n!}{\varGamma ( n + m + 1 )}}\).

The localized solution in Eq. (15A) has the pulse width, wave front curvature, phase, and other characteristics changing with the propagation distance. Thus, it does not represent a shape-invariant spatial soliton. However, from Eq. (14A) we see that for λ=1 the beam diffraction is exactly balanced by the nonlinearity. Since for λ=1 it is w(z)=w 0, the beam width is independent of the propagation distance z. In this case the beam becomes an exact soliton beam that is termed the resonance soliton. The parameter functions are then simplified as follows: w(z)=w 0, \(b( z ) = b_{0} - ( 2n + m + 1 )\frac{z}{w_{0}^{2}}\), \(s = \frac{1}{\sqrt{2} w_{0}^{2}}\), a(z)=0, and Eq. (1) admits the following analytical resonance soliton solutions:

$$ \begin{array}[b]{@{}lll} E_{j} ( z,r,\varphi ) &=& \displaystyle\frac{k ( A_{j}\cos m\varphi+ B_{j}\sin m\varphi )}{r}W_{nm} \biggl( \frac{r^{2}}{w_{0}^{2}} \biggr)\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\[4mm] &&{}\times U \bigl[ R ( z,r ) \bigr]e^{i [ b_{0} - \frac{2n}{w_{0}^{2}}z ]}. \end{array} $$
(15B)

From Eq. (15B), it is seen that the novel solitons are characterized by three parameters: the mode number n, TC m, and the modulation depth q. Based on the values of these parameters, we introduce new classes of 2D resonance scalar and vector solitons. Note that in this case, the auxiliary function R, the nonlinearity coefficient g, and the trapping potential V depend only on the radial variable r. Hence, to obtain shape-invariant solitons by the present method, it is necessary to have the nonlinearity coefficient that depends only on the transverse distance.

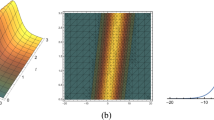
We first study the case when n and m are different non-negative integers. Selecting some specific values of the parameter q, we present plots of the intensity distributions with an initial condition w 0=1. It is easy to see that the solutions in Eq. (15B) are localized, since lim|r|→∞ E j (z,r,φ)=0. The distributions of the nonlinearity coefficient g(r) and the external potential V(r) with respect to the radial coordinate r are shown in Fig. 1. It should be pointed out that our procedure requires specific well-shaped external potentials and nonlinearity coefficients. Their forms are enforced by Eqs. (11) and (9B), which present a drawback in the procedure and in the applicability of the method. Thus, to obtain the nice analytical solution of Eq. (15B), one has to impose certain conditions on the nonlinearity coefficient and the external potential, which in principle are not known beforehand. On the other hand, the knowledge of analytical solutions presents an asset that can be used in the search of approximate quasi-stable solutions and of the materials that may display the required nonlinearity coefficients. In the same venue, the trapping external potential—which to leading order is parabolic and contains a term proportional to g—may be conveniently expanded in more realistic cases, to mimic the required form.

Fig. 1
figure 1

Distributions of the nonlinearity coefficient g(r) and the external potential V(r) for the resonance soliton from Eq. (15B). Parameters: w 0=1, n=m=0. Self-focusing material, G=1, μ=−0.001 (dashed line); self-defocusing material, G=−1, μ=0.008 (solid line) (Color figure online)

Full size image

3 The structure of resonance solitons

The structure of the analytical solution (15B) for resonance solitons can be controlled—as mentioned—by three parameters: n, m and q. We emphasize that the total angular momentum of the resonance soliton can be represented as \(M = \sum_{j = 1}^{N} M_{j} = mP^{( m)}\operatorname{Im} ( A_{j}^{ *} B_{j} )\), where \(P^{( m )} = 2\pi \int_{0}^{\infty} | u |^{2}r\,dr\) is the power of the resonance soliton with the topological charge m. The total power is expressed as \(P = \frac {1}{2}\sum_{j} ( | A_{j} |^{2} + | B_{j} |^{2} )P^{( m )} = P^{( m )}\). The ratio of the total angular momentum to the total power, \(\frac{M}{P} = m\operatorname{Im} ( A_{j}^{ *} B_{j} ) = \frac{2mq}{1 + q}\), can be regarded as an analogue of the spin of the resonance soliton (but is not formally equal to the actual spin of the optical field in question). Thus, the value of the spin depends on the parameters q and m. The spin is zero for q=0 and m=0, and is nonzero for 0<q≤1 and m≠0.

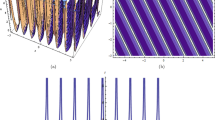
We begin by analyzing the scalar soliton (N=1) and select the lowest order (fundamental) solution of Eq. (15B) with bell-shaped (self-focusing material) or ring-shaped (self-defocusing material) distributions of the beams for m=0 and zero spin. Such a fundamental soliton can exist as a spatially localized excitation, that is, a 2D resonance scalar soliton. The solutions of Eq. (15B) are presented in Fig. 2. For μ<0 and G=1, the bell-shaped solutions of this type consist of several rings surrounding the central peak, see the top row in Fig. 2. We plot the intensity distributions (I=|u|2) for different n with the fixed topological charge m=0. The left panel, corresponding to n=0, is a fundamental soliton state. The middle and the right panels, corresponding to n=1,2, represent two excited states. It is seen that the number of rings increases with increasing n, while at the same time the optical intensity at the center decreases. For a fixed n (n>1), the intensity of rings surrounding the center peak increases slowly with increasing the radial distance.

Fig. 2
figure 2

Intensity profiles of scalar resonance solitons, for the parameters m=0, n=0,1,2 from left to right; top row, the self-focusing material, bottom row, the self-defocusing material (Color figure online)

Full size image

The bottom row in Fig. 2 depicts intensity profiles of the fundamental vortex solution, with μ>0 and G=−1. Now, the optical intensity in the center is zero, and the intensity of rings surrounding the center increases with the increasing radial distance.

Next, we discuss the vector resonance solitons from Eq. (15B) with nonzero TC (m≠0) and zero modulation depth (q=0), for m=6, q=0 and different n. The beam represents an incoherent superposition of two components. Each component of such a localized solution displays a necklace-type self-trapped structure, which consists of a large number of “petals”, and the total intensity distribution exhibits similar vortex profile. We present the dynamics of vector resonance solitons in Figs. 3, 4, 5 for n=0,1,2. In the figures, the symbols I=|E 1|2+|E 2|2, I 1=|E 1|2, and I 2=|E 2|2 stand for the total intensity, as well as intensities of the constituent components, respectively.

Fig. 3
figure 3

Top row: Intensity profiles of the soliton components and of the total soliton in the self-focusing material with G=1, μ=−1/2. Bottom row: The same, but for the self-defocusing material with G=−1, μ=1. Solutions correspond to the parameters q=0, n=0, and m=6 (Color figure online)

Full size image
Fig. 4
figure 4

The same as Fig. 3 except for n=1 (Color figure online)

Full size image
Fig. 5
figure 5

Radial distributions of the total intensity for different topological charges. Left: Self-focusing material; Right: Self-defocusing material. The parameters are the same as Fig. 3, except for n=2 (Color figure online)

Full size image

In the top row of panels in Fig. 3, we depict the intensity profiles in the self-focusing material, for G=1 and μ=−1/2. The bottom row depicts the profiles in the self-defocusing material, for G=−1 and μ=1. In the present work, unlike [16], self-trapped necklace solitons do not expand as they propagate; it is also different from the slowly expanding necklaces in Ref. [29]. One of the interesting properties to note is a wider extent of the resonant solitons in the self-defocusing materials than those in the self-focusing materials, under the same conditions, because of the self-defocusing effect. In Fig. 4 we present the same results for the vector resonance soliton when n=1.

To compare the properties of analytical solutions from (15B), we also display radial structures of the total optical intensity distributions (I=|u 1|2+|u 2|2) in Fig. 5, by choosing different topological charges m (m≠0) with fixed n=2. It is seen that the total optical intensity of the vortex states becomes less localized with increasing topological charge m, due to the larger angular momentum of the higher topological charge. Vector soliton becomes wider as the topological charge is increased and it possesses larger angular momentum. Similar results have been found numerically and have been generated experimentally in Ref. [30], in an anisotropic photorefractive medium.

Furthermore, we find that the larger the TC m with zero modulation depth, the smaller the total intensity of solitons for self-focusing materials, while for self-defocusing materials the opposite holds. The resonance soliton with the same parameters has larger optical intensity in the self-focusing material than in the self-defocusing material (see Fig. 5).

By increasing the modulation depth q from 0, one finds resonance solitons with changing azimuthal modulation—the azimuthons. The solitons still possess the vortex structure and carry nonzero angular momentum. In Figs. 6 and 7 we demonstrate two examples of azimuthons with four intensity peaks for each component of the vector soliton described by Eq. (15B). Incoherent interaction between the components of a vector necklace beam allows for compensation of the repulsion between beamlets, creating a new type of self-trapped structure that exhibits the properties of ring vortex solitons. The physical mechanism for creating such a composite vector ring soliton is similar to the mechanism responsible for the formation of the so-called solitonic gluons [31] and is explained by a balance of the forces acting between two incoherent components of a composite soliton. In that case, the mutual repulsion of the beamlets in the E 2-component is balanced by the incoherent attraction of the coupled E 1-component.

Fig. 6
figure 6

Evolution of vector necklace ring resonance solitons with nonzero modulation depth in each component. Top row is the self-focusing material, bottom row is the self-defocusing material. The parameters are q=0.75, n=0, m=2 (Color figure online)

Full size image
Fig. 7
figure 7

The same as Fig. 6, except for n=2 (Color figure online)

Full size image

Finally, we stress that the defocusing nonlinearity is a necessary ingredient for the existence of multi-peaked fundamental, low-order and high-order dark vortex ring solitons. A 2D NLS equation with defocusing nonlinearity was shown to support the fundamental vortex soliton solutions whose intensity vanishes at the vortex center and asymptotically approaches a constant value at infinity (see the bottom row in Fig. 2). Such vortex ring solitons were experimentally observed in a bulk self-defocusing optical medium [32]. The low-order vortices with m=1 are energetically favorable, which implies that instabilities of other families of solutions may result in the formation of only low-order vortices. In particular, a 2D vortex ring soliton stripe is unstable to long-wave symmetry-breaking perturbations, leading to the generation of low-order vortex soliton pairs with opposite vorticities [33, 34]. Higher-order vortices are also unstable and break down into low-order vortices. However, in the NLS limit no exponentially growing modes exist [35] and, as a consequence, multi-TC vortices are very long-lived objects. Strong instabilities of multi-TC vortices can be triggered by different mechanisms such as dissipation, nonlinearity saturation, or anisotropy [36]. Vortex beams observed in experiments exhibit some features expected from a dark vortex soliton, but a comprehensive investigation and understanding of these important observations is not yet fully achieved. Thus, the existence of stable dark vortices in a quadratic NL medium remains an open problem.

4 Stability analysis

The stability of scalar and vector vortex resonance solitons, especially for higher topological charges, is an important problem. The following discussion will focus on the stability of fundamental scalar and vector vortex solitons with different n, m, and q values in the self-focusing and self-defocusing materials. In this section, we investigate the stability of the analytical solution (15B) and show that stable fundamental scalar solitons and only some types of the vortices with m=1 can be supported by the azimuthal modulations in our model.

We perform direct numerical simulations using the split-step Fourier method [37] and solve Eq. (1) by taking the analytical solution (15B) at z=0 as an initial condition. We first present in Fig. 8 the scalar soliton, with parameters m=0, n=2. It is seen that the scalar solitons are stable. The comparison of analytical solutions from Fig. 2 with the numerical simulations in Fig. 8 reveals that the analytical solution is consistent with the numerical results.

Fig. 8
figure 8

Contour profiles of intensity distributions (nonzero in white annuli, zero in orange areas) for the fundamental resonance soliton. Top row is the self-focusing material, bottom row is the self-defocusing material. Left column is the analytical solution, right column the numerical simulation (Color figure online)

Full size image

Next, we select different topological charges m with the same parameters as in Fig. 7, but increase the modulation depth to q=0.96. In Fig. 9, we again display the optical intensity of analytical solution (15B) with n=2 and m=1,2,3 from top to bottom, which was used as an initial condition, and compare with solutions obtained in the numerical simulation of Eq. (1). It is seen that only when the topological charge is m=1 the numerical solution is stable against perturbation with an initial Gaussian noise level of 5 %. But when the topological charge is m≥2, the vector soliton solution (15B) is unstable in propagation and splits into necklace ring-shaped structures. We furthermore find that the stability of vector solution (15B) in the self-defocusing material is better than that in the self-focusing material. In fact, when q→1 the stability of vector resonance soliton solutions of Eq. (15B) improves, in that it propagates with little change for very long.

Fig. 9
figure 9

Comparison of analytical and numerical intensity distribution contour plots. Left two columns are for the self-focusing material, right two columns are for the self-defocusing material. The parameters are:q=0.96, n=2, and m=1,2,3 from top to bottom (Color figure online)

Full size image

5 Conclusions

In summary, we investigated the dynamics of azimuthally modulated resonance solitons in self-focusing and self-defocusing materials. Under the same parameters, the intensity of resonance solitons in the self-focusing material is larger than that in the self-defocusing material. The stability of the solitons is checked by direct numerical simulation. Our results show that the stability of resonance solitons in defocusing material is better than in the focusing material, and that the stability improves as q→1. We find that the scalar resonance solitons with zero topological charge and low-order vector solitons with m=1 are stable. But, for higher topological charges (m≥2), the vector vortex solitons are unstable. Our approach can be applied to other problems, e.g., Bose–Einstein condensates and light propagation in plasmas.