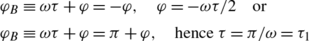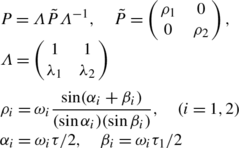New limit cycles of dry friction oscillators under harmonic load

Abstract

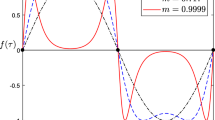
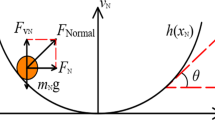
We consider a system composed of two masses connected by linear springs. One of the masses is in contact with a driving belt moving at a constant velocity. Friction force, with Coulomb’s characteristics, acts between the mass and the belt. Moreover, the mass is also subjected to a harmonic external force. Several periodic orbits including stick phases and slip phases are obtained. In particular, the existence of periodic orbits including a part where the mass in contact with the belt moves in the same direction at a higher speed than the belt itself is proved. Non-sticking orbits are also found for a non-moving belt. We prove that this kind of solution is symmetric in space and in time.

Appendices

Appendix 1

(38)

The natural frequencies (ω ₁,ω ₂) are the roots of the characteristic equation:

(39)

The eigenvectors , (j=1,2) are defined by $(K-I\omega_{j}^{2})\psi_{j}=0$.

These matrices fulfil the following property:

$$ H_{1}^{2}(t) - H_{2}(t)H_{3}(t) = 0, $$

(40)

(41)

The matrices Γ _i (t) fulfil also the property:

$$ {\varGamma}_{1}^{2}(t) - {\varGamma}_{2}(t){\varGamma}_{3}(t) = 0 $$

(42)

Appendix 2

For τ/2<t<τ, the periodic solution is defined by

$$ Z(\tau - t) = H(\tau - t)(Z_{0} - F_{0}) + F(\tau - t) $$

(43)

From the identities:

$$ \begin{array}{l} F(\tau - t) = EF(t),\quad \bigl(\hbox{i.e.}\ F(\tau) = EF_{0}\bigr) \\[6pt] H(\tau - t) = H(\tau)H(-t),\quad H(-t)E = EH(t) \end{array} $$

(44)

the first relation (17) is deduced.

For T/2<t ₁<T, the solution is defined by

$$ Z(t) = {\varGamma}(T - t_{1})EZ_{0} $$

(45)

From the identities:

$$ \begin{array}{l} {\varGamma}(T-t_{1}) = {\varGamma}(T){\varGamma}( - t_{1}), \\[6pt] E{\varGamma}(-t_{1}) = {\varGamma}(t_{1})E, \\[6pt] Z(\Theta) = {\varGamma}(T)EZ_{0} = Z_{0} \end{array} $$

(46)

the last relation (17) follows.

Appendix 3

$$ \begin{array}{lll} a_{1} &=& \tilde{H}_{11} - {\varGamma}_{11},\qquad b_{1} = \tilde{H}_{12} - {\varGamma}_{12}, \\[6pt] c_{1} &=& \tilde{H}_{13} - {\varGamma}_{13} \\[6pt] d_{1} &=& -\bigl(\tilde{H}_{11}q_{1} + \tilde{H}_{12}q_{2}\bigr)\cos\varphi \\ [6pt] && {} + \omega\bigl(\tilde{H}_{13}q_{1} + \tilde{H}_{14}q_{2}\bigr)\sin\varphi + q_{1}\cos\varphi_{C} \\[6pt] && {} + 2(h_{11}-1)d_{01} + 2h_{12}d_{02} + \bigl(\tilde{H}_{14} + {\varGamma}_{14}\bigr)V, \end{array} $$

(47)

$$ \begin{array}{lll} a_{2} &=& \tilde{H}_{21},\qquad b_{2} = \tilde{H}_{22} - 1,\qquad c_{2} = \tilde{H}_{23} \\[6pt] d_{2} &=& - \bigl(\tilde{H}_{21}q_{1} + \tilde{H}_{22}q_{2}\bigr)\cos\varphi \\[6pt] && {} + \omega\bigl(\tilde{H}_{23}q_{1} + \tilde{H}_{24}q_{2}\bigr)\sin\varphi + q_{2}\cos\varphi_{C} \\[6pt] && {} + 2h_{21}d_{01} + 2\bigl(h_{22} - 1\bigr)d_{02} + (\tilde{H}_{24} + T)V, \end{array} $$

(48)

$$ \begin{array}{lll} a_{3} &=& \tilde{H}_{31} + {\varGamma}_{31},\qquad b_{3} = \tilde{H}_{32} + {\varGamma}_{32}, \\[6pt] c_{3} &=& \tilde{H}_{11} - {\varGamma}_{11} \\[6pt] d_{3} &=& - \bigl(\tilde{H}_{31}q_{1} + \tilde{H}_{32}q_{2}\bigr)\cos\varphi \\[6pt] && {} + \omega\bigl(\tilde{H}_{11}q_{1} + \tilde{H}_{12}q_{2}\bigr)\sin\varphi - q_{1}\sin\varphi_{C} \\[6pt] && {} + 2h_{31}d_{01} + 2h_{32}d_{02} + \bigl(\tilde{H}_{12} - {\varGamma}_{12}\bigr)V, \end{array} $$

(49)

$$ \begin{array}{lll} a_{4} &=& H_{41},\qquad b_{4} = H_{42},\qquad c_{4} = H_{21}, \\[6pt] d_{4} &=& (H_{22} - 1)V - q_{2}\omega\sin(\varphi_{B}) \\[6pt] && {} - (H_{41}q_{1} + H_{42}q_{2})\cos\varphi \\[6pt] && {} + (H_{21}q_{1} + H_{22}q_{2})\omega\sin\varphi, \end{array} $$

(50)

$$ \begin{array}{lll} a_{5} &=& \tilde{H}_{41},\qquad b_{5} = \tilde{H}_{42},\qquad c_{5} = \tilde{H}_{21},\\[6pt] d_{5} &=& \bigl(\tilde{H}_{22} - 1\bigr)V - q_{2}\omega\sin(\varphi_{C}) \\[6pt] && {} - \bigl(\tilde{H}_{41}q_{1} + \tilde{H}_{42}q_{2}\bigr)\cos\varphi \\[6pt] && {} + \bigl(\tilde{H}_{21}q_{1} + \tilde{H}_{22}q_{2}\bigr)\omega\sin\varphi \\[6pt] && {} + 2(h_{41}d_{01} + h_{42}d_{02}) \end{array} $$

(51)

$$\begin{array}{l} H_{ij} = H_{ij}(\tau),\quad h_{ij} = H_{ij}(\tau_{1}),\quad \tilde{H}_{ij} = H_{ij}(\tau + \tau_{1}) \\[6pt] \varphi_{B} = \omega\tau + \varphi,\quad \varphi_{C} = \varphi_{B} + \omega\tau_{1} \end{array} $$

Appendix 4

From (5), (19) and (30), the non-sticking periodic orbit obtained with the assumption that τ=π/ω=Θ/2 is described by

(52)

Taking into account the properties

$$ F(t + \tau) = -F(t),\quad 0 \le t \le\tau,\quad X_{B} = - X_{0} $$

(53)

the symmetry of the motion is deduced:

$$ X(t) = -X(t + \tau),\quad 0 \le t \le\tau $$

(54)

Appendix 5

Let us consider the same kind of non-sticking periodic orbits as in Sect. 6, with V=0 but without the assumption τ=Θ/2.

For 0<t<τ, the motion is given by (5), while for τ<t<Θ, the motion is described by

(55)

A periodic motion of period Θ=2π/ω is obtained if Z(Θ)=Z ₀ or:

$$ \begin{array}{l} \bar{Z}_{0} = H(\tau_{1})\bigl(\bar{Z}_{B} - F_{B}\bigr) + F_{0}, \\[6pt] Z_{B} = Z(\tau) = H(\tau)(Z_{0} - F_{0}) + F_{B}, \\[6pt] F_{B} = F(\tau),\quad \tau_{1} = {\varTheta} - \tau,\quad \bar{Z}_{0} = \bar{Z}(0) \end{array} $$

(56)

From (56), we deduce:

$$ \begin{array}{l} \xi_{1}\equiv Z_{B} - F_{B} + E(Z_{0} - F_{0}) \\[6pt] \phantom{\xi_{1} } = \bigl(H(\tau) + E\bigr)(Z_{0} - F_{0}), \\[6pt] \xi_{2}\equiv \bar{Z}_{B} - F_{B} + E(\bar{Z}_{0} - F_{0}) \\[6pt] \phantom{\xi_{2} } = \bigl(H( - \tau_{1}) + E\bigr)(\bar{Z}_{0} - F_{0}) \end{array} $$

(57)

From the relations:

$$ H(t)E = E\bigl(H(t)\bigr)^{-1} = EH( - t) $$

(58)

it follows:

$$ \begin{array}{l} \bigl(H(-t)-E\bigr)\bigl(H(t) + E\bigr) = 0, \\[6pt] \bigl(H(t) - E\bigr)\bigl(H( - t) + E\bigr) = 0 \end{array} $$

(59)

From (57) and (59), we deduce

$$ \bigl(H(-\tau) - E\bigr)\xi_{1} = 0,\qquad \bigl(H(\tau_{1}) - E\bigr)\xi_{2} = 0 $$

(60)

On the other hand, it is not difficult to show that

$$ \xi_{1} - \xi_{2} = Z_{B} - \bar{Z}_{B} + E(Z_{0} - \bar{Z}_{0}) = 0 $$

(61)

Let us introduce the following notations:

(62)

From (60), it results:

$$ \begin{array}{l} Y_{1} = P_{1}X_{1},\quad P_{1} = H_{2}^{ - 1}(H_{1} + I), \\[6pt] Y_{2} = P_{2}X_{2},\quad P_{2} = - h_{2}^{ - 1}(h_{1} + I) \end{array} $$

(63)

The relations X ₁=X ₂,Y ₁=Y ₂, deduced from (61) are equivalent to:

$$ X_{1} = X_{2},\quad PX_{1} = 0,\quad P = P_{1} - P_{2} $$

(64)

From (64), two cases are obtained:

• 1. Det(P)≠0 leads to X ₁=0, hence

  $$ X_{2} = 0,\qquad Y_{1} = 0,\qquad Y_{2} = 0 $$

  (65)

  From (56) and (64), we deduce

  $$ \begin{array}{l} z_{B} - Q\cos\varphi_{B} = z_{0} - Q\cos\varphi, \\[6pt] z'_{B} + Q\omega\sin\varphi_{B} = - \bigl(z'_{0} + Q\omega\sin\varphi\bigr), \\[6pt]\ \bar{z}_{B} - Q\cos\varphi_{B} = \bar{z}_{0} - Q\cos\varphi \end{array} $$

  (66)

  From the relation:

  $$ \begin{array}{l} z'_{B} = - Q\omega\sin\varphi_{B} - \bigl(z'_{0} + Q\omega\sin\varphi\bigr), \\[6pt] z'_{2B} = z'_{20} = 0 \end{array} $$

  (67)

  we obtain sinφ _B =−sinφ, hence

  

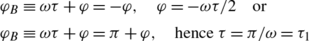
  In the first case, (φ _B ≡−φ,φ=−ωτ/2), from (67) $z'_{B} = - z'_{0}$ and from (66):

  $$z_{B} = z_{0} - Q\cos\varphi + Q\cos\varphi_{B} = z_{0} $$

  which is impossible because for 0<t<τ, $z'_{2}<0$, hence: z _2B <z ₂₀.

  In the second case, (τ=π/ω=τ ₁), hence H _i =h _i , i=1,2,3

  $$z_{B} + Q\cos\varphi = z_{0} - Q\cos\varphi,\quad \hbox{i.e.}, $$

  x _B +Qcosφ=x ₀−Qcosφ.

  From (56), we get

  $$ \begin{array}{l} z_{B} + \bar{z}_{B} + 2Q\cos\varphi \\[6pt] \quad = H_{1}(z_{0} + \bar{z}_{0} - 2Q\cos\varphi)\quad \hbox{i.e.}\\[6pt] x_{B} + Q\cos\varphi \\[6pt] \quad = H_{1}(x_{0} - Q\cos\varphi) = x_{0} - Q\cos\varphi \end{array} $$

  (68)

  Hence, if det(H ₁−I)≠0, we obtain

  $$ x_{0} = Q\cos\varphi,\qquad x_{B} = - Q\cos\varphi = - x_{0} $$

  (69)

• 2. Det(P)=0

  From $P=H_{2}^{-1}(H_{1}+I)+h_{2}^{ - 1}(h_{1} + I)$: we deduce

  

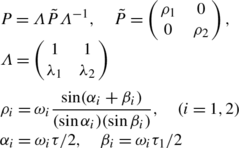  (70)

  It results Det(P)=0 if sin(α _i +β _i )≡sin(ω _i π/ω)=0, i.e., ω _i =kω, (k=1,2,…) (resonance).

  Except this particular case of resonance with the natural frequencies of the system, only symmetrical periodic solutions with a phase of slipping motion and a phase of overshooting motion exist.