Skip to main content
SpringerLink
Log in

A novel non-equilibrium fractional-order chaotic system and its complete synchronization by circuit implementation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

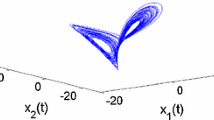
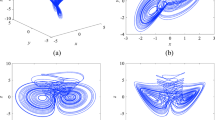
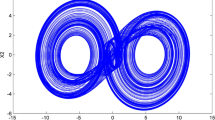
In this paper, we construct a novel four dimensional fractional-order chaotic system. Compared with all the proposed chaotic systems until now, the biggest difference and most attractive place is that there exists no equilibrium point in this system. Those rigorous approaches, i.e., Melnikov’s and Shilnikov’s methods, fail to mathematically prove the existence of chaos in this kind of system under some parameters. To reconcile this awkward situation, we resort to circuit simulation experiment to accomplish this task. Before this, we use improved version of the Adams–Bashforth–Moulton numerical algorithm to calculate this fractional-order chaotic system and show that the proposed fractional-order system with the order as low as 3.28 exhibits a chaotic attractor. Then an electronic circuit is designed for order q=0.9, from which we can observe that chaotic attractor does exist in this fractional-order system. Furthermore, based on the final value theorem of the Laplace transformation, synchronization of two novel fractional-order chaotic systems with the help of one-way coupling method is realized for order q=0.9. An electronic circuit is designed for hardware implementation to synchronize two novel fractional-order chaotic systems for the same order. The results for numerical simulations and circuit experiments are in very good agreement with each other, thus proving that chaos exists indeed in the proposed fractional-order system and the one-way coupling synchronization method is very effective to this system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Tavazoei, M.S., Haeri, M.: A proof for non existence of periodic solutions in time invariant fractional-order systems. Automatica 45, 1886–1890 (2009)

    Article  MATH  Google Scholar 

  2. Westerlund, S., Ekstam, L.: Capacitor theory. IEEE Trans. Dielectr. Electr. Insul. 1, 826–839 (1994)

    Article  Google Scholar 

  3. Jenson, V.G., Jeffreys, G.V.: Mathematical Methods in Chemical Engineering. Academic Press, New York (1977)

    MATH  Google Scholar 

  4. Sun, H.H., Abdelwahad, A.A., Onaral, B.: Linear approximation of transfer function with a pole of fractional-order. IEEE Trans. Autom. Control 29, 441–444 (1984)

    Article  MATH  Google Scholar 

  5. Ichise, M., Nagayanagi, T., Kojima, T.: An analog simulation of non-integer order transfer functions for analysis of electrode process. J. Electroanal. Chem. 33, 253–265 (1971)

    Article  Google Scholar 

  6. Heaviside, O.: Electromagnetic Theory. Academic Press, New York (1971)

    Google Scholar 

  7. Bagley, R.L., Calico, R.A.: Fractional-order state equations for the control of visco-elastically damped structures. J. Guide Conteol Dyn. 14, 304–311 (1991)

    Article  Google Scholar 

  8. Kusnezov, D., Bulgac, A., Dang, G.D.: Quantum levy processes and fractional kinetics. Phys. Rev. Lett. 82, 1136–1139 (1999)

    Article  Google Scholar 

  9. Laskin, N.: Fractional market dynamics. Physica A 278, 482–492 (2000)

    Article  MathSciNet  Google Scholar 

  10. EI-Sayed, A.M.A.: Fractional-order diffusion wave equation. Int. J. Theory Phys. 35, 311–322 (1996)

    Article  Google Scholar 

  11. Yang, Q.G., Zeng, C.B.: Chaos in fractional conjugate Lorenz system and its scaling attractors. Commun. Nonlinear Sci. Numer. Simul. 15, 4041–4051 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  12. Gao, X., Yu, J.B.: Chaos in the fractional-order periodically forced complex Duffing’s oscillators. Chaos Solitons Fractals 26, 1125–1133 (2005)

    Article  MathSciNet  Google Scholar 

  13. Hartley, T.T., Lorenzo, C.F., Qammer, H.K.: Chaos on a fractional Chua’s system. IEEE Trans. Circuits Syst. I, Fundam. Theory Appl. 42, 485–490 (1995)

    Article  Google Scholar 

  14. Li, C.P., Peng, G.J.: Chaos in Chen’s system with a fractional-order. Chaos Solitons Fractals 20, 443–450 (2004)

    Article  MathSciNet  Google Scholar 

  15. Lu, J.G.: Chaotic dynamics of the fractional-order Lü system and its synchronization. Phys. Lett. A 354, 305–311 (2006)

    Article  Google Scholar 

  16. Wang, J.W., Zhang, Y.B.: Designing synchronization schemes for chaotic fractional-order unified systems. Chaos Solitons Fractals 30, 1265–1272 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  17. Grigorenko, I., Grigorenko, E.: Chaotic dynamics of the fractional-order Lorenz system. Phys. Rev. Lett. 91, 034101 (2003)

    Article  Google Scholar 

  18. Li, C.P., Chen, G.R.: Chaos and hyperchaos in the fractional-order Rössler equations. Physica A 341, 55–61 (2004)

    Article  MathSciNet  Google Scholar 

  19. Charef, A., Sun, H., Tsao, B., Onaral, B.: Fractal systems as represented by singularity function. IEEE Trans. Autom. Control 37, 1465–1470 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  20. Adomian, G.: A review of the decomposition method and some recent results for nonlinear equation. Math. Comput. Model. 13, 17–43 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  21. Diethelm, K., Ford, N.J., Freed, A.D.: A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 29, 3–22 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  22. Cafagna, D., Grassi, G.: Fractional-order chaos: a novel four-wing attractor in coupled Lorenz systems. Int. J. Bifurc. Chaos 19, 3329–3338 (2009)

    Article  MATH  Google Scholar 

  23. Gejji, D., Jafari, H.: Adomian decomposition: a tool for solving a system of fractional differential equations. J. Math. Anal. Appl. 301, 508–518 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  24. Tavazoei, M.S., Haeri, M.: Limitations of frequency domain approximation for detecting chaos in fractional-order systems. Nonlinear Anal. 69, 1299–1320 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  25. Adomian, G.: Solving Frontier Problems of Physics: The Decomposition Method. Kluwer Academic, Boston (1994)

    MATH  Google Scholar 

  26. Gao, X., Yu, J.B.: Chaos in the fractional-order periodically forced complex Duffing’s oscillators. Chaos Solitons Fractals 26, 1097–1104 (2005)

    Article  MathSciNet  Google Scholar 

  27. Lu, J.G.: A note on the fractional-order Chen system. Chaos Solitons Fractals 27, 685–688 (2006)

    Article  MATH  Google Scholar 

  28. Peng, G., Jiang, Y., Chen, F.: Generalized projective synchronization of fractional-order chaotic systems. Physica A 387, 3738–3746 (2008)

    Article  Google Scholar 

  29. Peng, G., Jiang, Y.: Generalized projective synchronization of a class of fractional-order chaotic systems via a scalar transmitted signal. Phys. Lett. A 372, 3963–3970 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  30. Deng, W.H., Li, C.P.: Chaos synchronization of the fractional Lü system. Physica A 353, 61–72 (2005)

    Article  Google Scholar 

  31. Samko, S.G., Klibas, A.A., Marichev, O.I.: Fractional Integrals and Derivatives: Theory and Applications. Gordan and Breach, Amsterdam (1993)

    MATH  Google Scholar 

  32. Peng, G.J., Jiang, Y.L.: Two routes to chaos in the fractional Lorenz system with dimension continuously varying. Physica A 389, 4140–4148 (2010)

    Article  MathSciNet  Google Scholar 

  33. Muth, E.J.: Transform Methods with Applications to Engineering and Operations Research. Prentice Hall, Englewood Cliffs (1977)

    MATH  Google Scholar 

  34. Charef, A., Sun, H.H., Tsao, Y.Y., Onaral, B.: Fractal system as represented by singularity function. IEEE Trans. Autom. Control 37, 1465–1470 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  35. Ahmad, W.M., Sprott, J.C.: Chaos in fractional-order autonomous nonlinear systems. Chaos Solitons Fractals 16, 339–351 (2003)

    Article  MATH  Google Scholar 

  36. Yu, Y.G., Li, H.X.: The synchronization of fractional-order Rössler hyperchaotic systems. Physica A 11, 1393–1403 (2007)

    MathSciNet  Google Scholar 

  37. Grigorenko, I., Grigorenko, E.: Chaotic Dynamics of the Fractional Lorenz System. Phys. Rev. Lett. 91, 034101 (2003)

    Article  Google Scholar 

  38. Zeng, C.B., Yang, Q.G., Wang, J.W.: Chaos and mixed synchronization of a new fractional-order system with one saddle and two stable node-foci, Nonlinear Dynamics. doi:10.1007/s11071-010-9904-2

Download references

Author information

Authors and Affiliations

  1. State Key Lab. of Power Transmission Equipment & System Security and New Technology, College of Computer Science, Chongqing University, Chongqing, 400044, PR China

    Huaqing Li & Xiaofeng Liao

  2. College of Automation, Chongqing University of Posts and Telecommunications, Chongqing, 400065, PR China

    Mingwei Luo

Authors
  1. Huaqing Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaofeng Liao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mingwei Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Huaqing Li.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, H., Liao, X. & Luo, M. A novel non-equilibrium fractional-order chaotic system and its complete synchronization by circuit implementation. Nonlinear Dyn 68, 137–149 (2012). https://doi.org/10.1007/s11071-011-0210-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-011-0210-4

Keywords

Search

Navigation