Skip to main content

Advertisement

SpringerLink
Log in

Nonlinear dynamics and chaos methods in neurodynamics and complex data analysis

  • Review Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

In this paper, we review modern nonlinear dynamical methods used in neuroscience and complex data analysis. We start with the general description of nonlinear dynamics, its geometrical (and topological) picture, as well as its extreme case, deterministic chaos, including its most popular models and methods: Lorenz attractor, Lyapunov exponents, and Kolmogorov–Sinai entropy.

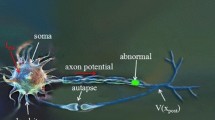
Then we review the most important nonlinear models in modern computational neuroscience: (i) Spiking and bursting neurons, including: integrate-and-fire neuron (linear and quadratic, without and with adaptation as well as bursting), complex-valued resonate-and-fire neuron, FitzHugh–Nagumo neuron, Hindmarsh–Rose thalamic neuron, Morris–Lecar neuron, Wilson–Cowan model of interacting neural populations, as well as classical (more general) Hodgkin–Huxley and FitzHugh–Nagumo neural models; (ii) Synchronization in oscillatory neural networks, based on oscillatory phase neurodynamics of the famous Kuramoto network model; and (iii) Neural attractor dynamics, based on Amari’s neural field theory and its application to behavioral and motivational autonomous robot dynamics.

Similarly, we review nonlinear and chaos methods suitable for complex data analysis, including: (i) Basic nonlinear analysis of the heart interbeat time series (with phase plots of delayed data and its approximate entropy calculations); (ii) Lyapunov spectrum and the related fractal and Kaplan–Yorke dimensions; (iii) Other chaotic dimensions and entropies of the complex data structures; and (iv) Medical applications to breast cancer diagnosis and preterm birth analysis.

The main application of all presented tools is in various areas of medical diagnosis. Other applications include Grossberg–Arbib type brain modeling, autonomous robotics, nonlinear, and adaptive control, as well as nonlinear data classification.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Amari, S.: Dynamics of pattern formation in lateral-inhibition type neural fields. Biol. Cybern. 27, 77–87 (1977)

    Article  MATH  MathSciNet  Google Scholar 

  2. Arbib, M. (ed.): Handbook of Brain Theory and Neural Networks, 2nd edn. MIT Press, Cambridge (1998)

    Google Scholar 

  3. Badii, R., Politi, A.: Statistical description of chaotic attractors. J. Stat. Phys. 40, 725 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  4. Beck, C., Schlögl, F.: Thermodynamics of Chaotic Systems. Cambridge Univ. Press, Cambridge (1993)

    Google Scholar 

  5. Benettin, G.: Power law behaviour of Lyapunov exponents in some conservative dynamical systems. Physica D 13, 211–213 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  6. Benettin, G., Giorgilli, A., Galgani, L., Strelcyn, J.M.: Lyapunov exponents for smooth dynamical systems and for Hamiltonian systems; a method for computing all of them. Part 1: Theory, and Part 2: Numerical applications. Meccanica 15, 9–30 (1980)

    Article  MATH  Google Scholar 

  7. Boffetta, G., Lacorata, G., Vulpiani, A.: Introduction to chaos and diffusion. Chaos in geophysical flows. In: International Summer School on Atmospheric and Oceanic Sciences (2001)

  8. Boffetta, G., Cencini, M., Falcioni, M., Vulpiani, A.: Predictability: a way to characterize complexity. Phys. Rep. 356, 367–474 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  9. Caiani, L., Casetti, L., Clementi, C., Pettini, M.: Geometry of dynamics, Lyapunov exponents, and phase transitions. Phys. Rev. Lett. 79, 4361–4364 (1997)

    Article  Google Scholar 

  10. Chen, G., Dong, X.: From Chaos to Order: Methodologies, Perspectives and Application. World Scientific, Singapore (1998)

    MATH  Google Scholar 

  11. Chirikov, B.V.: A universal instability of many-dimensional oscillator systems. Phys. Rep. 52, 264–379 (1979)

    Article  MathSciNet  Google Scholar 

  12. Eckmann, J.P., Ruelle, D.: Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 57, 617 (1985)

    Article  MathSciNet  Google Scholar 

  13. Eisenhart, L.P.: Dynamical trajectories and geodesics. Math. Ann. 30, 591–606 (1929)

    MathSciNet  Google Scholar 

  14. Ermentrout, G.B.: The behavior of rings of coupled oscillators. J. Math. Biol. 12, 327 (1981)

    Article  MATH  MathSciNet  Google Scholar 

  15. FitzHugh, R.A.: Impulses and physiological states in theoretical models of nerve membrane. Biophys J. 1, 445–466 (1961)

    Article  Google Scholar 

  16. FitzHugh, R.A.: Mathematical models of excitation and propagation in nerve. In: Schwan, H.P. (ed.) Biological Engineering. McGraw-Hill, New York (1969)

    Google Scholar 

  17. Franzosi, R., Casetti, L., Spinelli, L., Pettini, M.: Topological aspects of geometrical signatures of phase transitions. Phys. Rev. E 60, 5009 (1999)

    Article  Google Scholar 

  18. Franzosi, R., Pettini, M.: Theorem on the origin of phase transitions. Phys. Rev. Lett. 92(6), 060601 (2004)

    Article  Google Scholar 

  19. Franzosi, R., Pettini, M., Spinelli, L.: Topology and phase transitions: a paradigmatic evidence. Phys. Rev. Lett. 84, 2774–2777 (2000)

    Article  Google Scholar 

  20. Grassberger, P.: Finite sample corrections to entropy and dimension estimates. Phys. Lett. A 128, 369 (1988)

    Article  MathSciNet  Google Scholar 

  21. Grote, C., Schöner, G.: Context-sensitive generation of goal-directed behavioral sequences based on neural attractor dynamics. In: Proceedings of the ISR/ROBOTIK2006 Joint Conference on Robotics, Munich, Germany, May (2006)

  22. Haken, H.: Synergetics: An Introduction, 3rd edn. Springer, Berlin (1983)

    MATH  Google Scholar 

  23. Haken, H.: Advanced Synergetics: Instability Hierarchies of Self-Organizing Systems and Devices, 3rd edn. Springer, Berlin (1993)

    Google Scholar 

  24. Haken, H.: Brain Dynamics, Synchronization and Activity Patterns in Pulse-Coded Neural Nets with Delays and Noise. Springer, New York (2002)

    Google Scholar 

  25. Hegger, R., Kantz, H., Schreiber, T.: Practical implementation of nonlinear time series methods: The TISEAN package. Chaos 9, 413 (1999)

    Article  MATH  Google Scholar 

  26. Hilborn, R.C.: Chaos and Nonlinear Dynamics: An Introduction for Scientists and Engineers. Oxford University Press, New York (1994)

    MATH  Google Scholar 

  27. Ho, K.K.L., et al.: Predicting survival in heart failure case control subjects by use of fully automated methods for deriving nonlinear and conventional indices of heart rate dynamics. Circulation 96, 842–848 (1997)

    Google Scholar 

  28. Hodgkin, A.L., Huxley, A.F.: A quantitative description of membrane current and application to conduction and excitation in nerve. J. Physiol. 117, 500–544 (1952)

    Google Scholar 

  29. Hoppensteadt, F.C., Izhikevich, E.M.: Weakly Connected Neural Networks. Springer, New York (1997)

    Google Scholar 

  30. Ivancevic, V., Ivancevic, T.: Human-Like Biomechanics: A Unified Mathematical Approach to Human Biomechanics and Humanoid Robotics. Springer, Dordrecht (2005)

    Google Scholar 

  31. Ivancevic, V., Ivancevic, T.: Geometrical Dynamics of Complex Systems. Springer, Dordrecht (2006)

    Book  MATH  Google Scholar 

  32. Ivancevic, V., Ivancevic, T.: High-Dimensional Chaotic and Attractor Systems. Springer, Dordrecht (2006)

    Google Scholar 

  33. Ivancevic, V., Ivancevic, T.: Natural Biodynamics. World Scientific, Singapore (2006)

    Google Scholar 

  34. Ivancevic, V., Ivancevic, T.: Neuro-Fuzzy Associative Machinery for Comprehensive Brain and Cognition Modelling. Springer, Berlin (2007)

    MATH  Google Scholar 

  35. Ivancevic, V., Ivancevic, T.: Computational Mind: A Complex Dynamics Perspective. Springer, Berlin (2007)

    MATH  Google Scholar 

  36. Ivancevic, V., Ivancevic, T.: Complex Dynamics: Advanced System Dynamics in Complex Variables. Springer, Dordrecht (2007)

    MATH  Google Scholar 

  37. Ivancevic, V., Ivancevic, T.: Applied Differential Geometry: A Modern Introduction. World Scientific, Singapore (2007)

    MATH  Google Scholar 

  38. Ivancevic, V., Ivancevic, T.: Complex Nonlinearity: Chaos, Phase Transitions, Topology Change and Path Integrals. Springer, Berlin (2008)

  39. Izhikevich, E.M.: Class 1 neural excitability, conventional synapses, weakly connected networks, and mathematical foundations of pulse-coupled models. IEEE Trans. Neu. Netw. 10, 499–507 (1999)

    Article  Google Scholar 

  40. Izhikevich, E.M.: Resonate-and-fire neurons. Neu. Netw. 14, 883–894 (2001)

    Article  Google Scholar 

  41. Izhikevich, E.M.: Which model to use for cortical spiking neurons? IEEE Trans. Neu. Netw. 15, 1063–1070 (2004)

    Article  Google Scholar 

  42. Kantz, H.: A robust method to estimate the maximal Lyapunov exponent of a time series. Phys. Lett. A 185, 77 (1994)

    Article  Google Scholar 

  43. Kaplan, J., Yorke, J.: Chaotic behavior of multidimensional difference equations. In: Peitgen, H.O., Walther, H.O. (eds.) Functional Differential Equations and Approximation of Fixed Points. Springer, New York (1987)

    Google Scholar 

  44. Kaplan, D.T., Furman, M.I., Pincus, S.M., Ryan, S.M., Lipsitz, L.A., Goldberg, A.L.: Aging and the complexity of cardiovascular dynamics. Biophys. J. 59, 945–949 (1991)

    Article  Google Scholar 

  45. Kuramoto, Y.: Chemical Oscillations. Waves and Turbulence. Springer, New York (1984)

    MATH  Google Scholar 

  46. Lorenz, E.N.: Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141 (1963)

    Article  Google Scholar 

  47. Mattfeldt, T.: Nonlinear deterministic analysis of tissue texture: a stereological study on mastopatic and mammary cancer tissue using chaos theory. J. Microsc. 185(1), 47–66 (1997)

    Article  Google Scholar 

  48. Morris, C., Lecar, H.: Voltage oscillations in the barnacle giant muscle fiber. Biophys. J. 35, 193–213 (1981)

    Article  Google Scholar 

  49. Nagumo, J., Arimoto, S., Yoshizawa, S.: An active pulse transmission line simulating 1214-nerve axons. Proc. IRL 50, 2061–2070 (1960)

    Article  Google Scholar 

  50. Oczeretko, E., Kitlas, A., Swiatecka, J., Laudanski, T.: Fractal analysis of the uterine contractions. Rivista di Biologia (Biol. Forum) 97(3), 499–504 (2004)

    Google Scholar 

  51. Oczeretko, E., Kitlas, A., Swiatecka, J., Borowska, M., Laudanski, T.: Nonlinear dynamics in uterine contractions analysis. In: Losa, G., Merlini, D., Nonnemacher, T., Weibel, E. (eds.) Fractals in Biology and Medicine, vol. IV, pp. 215–222. Birkhäuser, Basel (2005)

    Chapter  Google Scholar 

  52. Oczeretko, E., Swiatecka, J., Kitlas, A., Laudanski, T., Pierzynski, P.: Visualization of synchronization of the uterine contraction signals: Running cross-correlation and wavelet running cross-correlation methods. Med. Eng. Phys. 28, 75–81 (2006)

    Article  Google Scholar 

  53. Ott, E., Grebogi, C., Yorke, J.A.: Controlling chaos. Phys. Rev. Lett. 64, 1196–1199 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  54. Ott, E.: Chaos in Dynamical Systems. Cambridge University Press, Cambridge (1993)

    MATH  Google Scholar 

  55. Pierzynski, P., Oczeretko, E., Laudanski, P., Laudanski, T.: New research models and novel signal analysis in studies on preterm labor: a key to progress? BMC Pregnancy Childbirth 7(Suppl. 1), S6 (2007)

    Article  Google Scholar 

  56. Pikkujamsa, S.M., et al.: Cardiac interbeat interval dynamics from childhood to senescence: Comparison of conventional and new measures based on fractals and chaos. Circulation 100, 393–399 (1999)

    Google Scholar 

  57. Pincus, S.: Approximate entropy (ApEn) as a complexity measure. Chaos 5, 110–117 (1995)

    Article  Google Scholar 

  58. Radharkrishnan, N., Wilson, J.D., Lowery, C., Eswaran, H., Murphy, P.: A fast algorithm for detecting contractions in uterine electromyography. IEEE Eng. Med. Biol. 19(2), 89–94 (2000)

    Article  Google Scholar 

  59. Rose, R.M., Hindmarsh, J.L.: The assembly of ionic currents in a thalamic neuron. I The three-dimensional model. Proc. R. Soc. Lond. B 237, 267–288 (1989)

    Google Scholar 

  60. Rosenstein, M.T., Collins, J.J., De Luca, C.J.: A practical method for calculating largest Lyapunov exponents from small data sets. Physica D 65, 117 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  61. Sauer, T., Yorke, J.: How many delay coordinates do you need? Int. J. Bifurc. Chaos 3, 737 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  62. Schöner, G., Dose, M.: A dynamical systems approach to task-level system integration used to plan and control autonomous vehicle motion. Robotics Autom. Syst. 10, 253–267 (1992)

    Article  Google Scholar 

  63. Schöner, G., Dose, M., Engels, C.: Dynamics of behavior: theory and applications for autonomous robot architectures. Robotics Autom. Syst. 16, 213–245 (1995)

    Article  Google Scholar 

  64. Schöner, G.: Dynamical Systems Approaches to Cognition. In: Sun, R. (ed.) Cambridge Handbook of Computational Cognitive Modeling. Cambridge University Press, Cambridge (2007)

    Google Scholar 

  65. Schnitzler, A., Gross, J.: Normal and pathological oscillatory communication in the brain. Nat. Rev. Neurosci. 6, 285–296 (2005)

    Article  Google Scholar 

  66. Sharma, S.: An exploratory study of chaos in human-machine system dynamics. IEEE Trans. Syst. Man Cybern. B 36(2), 319–326 (2006)

    Article  Google Scholar 

  67. Sparrow, C.: The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors. Springer, New York (1982)

    MATH  Google Scholar 

  68. Strogatz, S.H.: From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Physica D 143, 1–20 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  69. Williams, G.P.: Chaos Theory Tamed. Joseph Henry, Washington (1997)

    MATH  Google Scholar 

  70. Wilson, H.R., Cowan, J.D.: Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 12, 1–24 (1972)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Electrical and Information Engineering, University of South Australia, Mawson Lakes Boulevard, Mawson Lakes Campus, Mawson Lakes, South Australia, 5095, Australia

    Tijana Ivancevic, Lakhmi Jain, John Pattison & Alex Hariz

Authors
  1. Tijana Ivancevic
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lakhmi Jain
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. John Pattison
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Alex Hariz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tijana Ivancevic.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ivancevic, T., Jain, L., Pattison, J. et al. Nonlinear dynamics and chaos methods in neurodynamics and complex data analysis. Nonlinear Dyn 56, 23–44 (2009). https://doi.org/10.1007/s11071-008-9376-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-008-9376-9

Keywords

Search

Navigation