1 Introduction

Floods cause significant damage to infrastructure and the community (Al Baky et al. 2020). For example, on average annual flood damage is over $40 billion globally, according to the Organization for Economic Cooperation and Development. In Australia, the average annual flood damage cost is over $400 million. Since the beginning of 2021, flood damage cost has been well over $200 million only in New South Wales (NSW), according to the Insurance Council of Australia. In some years, flood damage is enormous in Australia. For example, during 2010–2011, the flood damage cost in Australia was estimated to be more than $30 billion (Carter 2012). Design flood is defined as a flood discharge that is associated with a return period and widely used in the hydrologic design. Flood frequency analysis is the most direct method to estimate design floods, which, however, needs a significant quantity of recorded flood data at the site of interest. There are numerous ungauged catchments where there is no recorded flood data; for these ungauged catchments, we use regional flood frequency analysis (RFFA) to estimate design floods. RFFA attempts to transfer flood characteristics information from gauged catchments to ungauged ones (Haddad and Rahman 2012).

There are many RFFA techniques that have been proposed in different countries, such as Probabilistic Rational Method (Pilgrim et al. 1987; Rahman et al. 2010), Index Flood Method (IFM) (Dalrymple 1960; Formetta et al. 2018; Kalai et al. 2020; Mosaffaie 2015; Stedinger and Lu 1995; Strnad et al. 2020; Yang 2016), Quantile Regression Techniques (QRT) (Ahn and Palmer 2016; Formetta et al. 2021; Haddad et al. 2015; Mosaffaie 2015; Rahman 2005; Rahman et al. 2020), Parameter Regression Technique (PRT) (Ahn and Palmer 2016; Haddad and Rahman 2012; Haddad et al. 2015; Perez et al. 2019), artificial intelligence based methods (Aziz et al. 2017; Janizadeh and Vafakhah 2021; Khan et al. 2021; Rahman et al. 2019b; Sharifi Garmdareh et al. 2018; Zalnezhad et al. 2022a, b, c) and some mixed and combined methods (Ahn and Palmer 2016; Allahbakhshian-Farsani et al. 2020; Aziz et al. 2013; Brodie 2013; Formetta et al. 2021; Janizadeh and Vafakhah 2021; Mosavi et al. 2018; Rahman and Rahman 2020; Vafakhah et al. 2020).

There have been some studies that compared different RFFA techniques. For example, Mosaffaie (2015) used 15 gauged catchments in Iran to compare IFM and multiple regression-based methods. He asserted that results from IFM are more reliable than the regression-based method. Haddad and Rahman (2012) proposed an approach based on Bayesian Generalized Least Squares (BGLS) regression in a region-of-influence (ROI) framework to compare QRT and PRT. They used data from 399 catchments and found that using BGLS-ROI approach enhanced the performance of both models as compared to fixed region approach. They also suggested that PRT performed better or at least equal to the QRT and hence they recommended PRT for application in Australia. Perez et al. (2019) used 5000 sites in USA to compare four different RFFA methods (IFM, QRT, PRT and an at-site flood frequency analysis) and found that the accuracy of the methods depends on model assumptions, parameter estimation method, sample size and the size of the proposed regions. They also noted that skewness affects the relative accuracy of the RFFA methods. Rahman et al. (2020) compared QRT and PRT using data from 88 catchments in NSW, Australia using independent component (IC) regression. They showed that the QRT model with four catchment characteristics provided less absolute median relative error than the PRT model with all the ICs as predictors. Formetta et al. (2021) investigated the efficiency of IFM to assess its applicability as compared to other RFFA methods in UK. Based on 540 catchments, they found that 30–70% of the peak flow variability can be explained by the catchment area. They discovered that QRT based on pooling group outperformed UK Flood Estimation Handbook method.

Research conducted by Ahn and Palmer (2016) compared the accuracy of two popular models, QRT and PRT, based on data from 237 catchments in USA. In this research, by using spatial proximity based RFFA methods, 30 catchment characteristics were investigated to find out the most important predictor variables. They suggested that PRT, due to its accuracy and simplicity, is more favourable than QRT.

There have been limited comparative studies on RFFA, for Australia. Hence this study is devoted to comparing two popular RFFA techniques, QRT and IFM, using the latest data set in Australia. Hence, the objectives of this study are: (i) to compile relevant data from a large number of natural gauged catchments in Australia, which can be used to develop and test new RFFA techniques; (ii) to develop IFM and QRT for the selected catchments; (iii) to compare IFM and QRT by an independent testing; and (iv) to compare our results with similar Australian and international studies. It is expected that the findings of this study will form new scientific basis to upgrade the RFFA techniques in Australia.

2 Study area and data

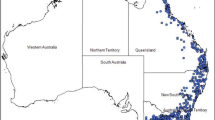
This study focuses on southeast Australia as high-quality streamflow data is available in this part of Australia compared to other regions. In selecting the study catchments, a set of selection criteria was adopted as noted below. The area of the catchment must be smaller than 1000 km2 as very large catchments possess different flood frequency behaviour than that of smaller catchments. The catchment must be natural without a major regulation (such as dam) and there should not be any land use changes over the period of streamflow data availability. The catchment should have a valid rating curve and the streamflow data quality should be rated as ‘good’ by the gauging authority. Based on these criteria, a total of 181 gauged catchments are selected from New South Wales (NSW) and Victoria. Amongst these, 55 catchments were selected randomly as test catchments leaving 126 catchments for model development. Figure 1 shows the locations of selected 181 catchments. The range of streamflow record lengths of these 181 catchments ranges from 40 to 89 years (average = 48 years). The reason for selecting these variables are that in previous Australian studies, these have been found to be significant in RFFA (e.g. Haddad and Rahman 2012; Rahman 1997). To estimate flood quantiles of annual exceedance probabilities (AEPs) of 1 in 2 (Q2), 1 in 5 (Q5), 1 in 10 (Q10), 1 in 20 (Q20), 1 in 50 (Q50) and 1 in 100 (Q100), a Log Pearson Type 3 distribution was adopted as it has been found to be the best-fitting probability distribution in Australia (Rahman et al. 2013). In fitting the LP3 distribution, a Bayesian fitting procedure based on the method of moments is adopted (Kuczera and Franks 2019).

Fig. 1
figure 1

Location of the selected catchments used for training and testing models

Full size image

A total of eight predictor variables (Table 1), as discussed below, are selected in this study as these have been found to be significant variables in RFFA in Australia (Haddad and Rahman 2012; Rahman et al. 2020).

Table 1 Summary of independent and dependent variables data for 181 study catchments
Full size table

2.1 Catchment area

The area of a catchment (AREA) is one of the main factors in predicting flood quantiles. In almost all previous RFFA studies, AREA has been used. Many other catchment characteristics such as slope, stream order and stream length are closely related to AREA (Anderson 1957; Rahman 1997). The area is the most used morphometric characteristic amongst the other characteristics, and it is known to be the main scaling factor in statistical hydrology. AREA was measured for each of the selected catchments by planimeter on the topographic map of 1:100,000 scale and validated by the recorded AREA in the catchment database of the relevant gauging authority.

2.2 Design rainfall intensity (I62)

Rahman (1997) asserted that rainfall intensity is one of the characteristics that have the most impact on the flood generation process whilst it is easy to be acquired. In RFFA studies, duration and AEP are the two factors that need to be selected appropriately whilst defining rainfall intensity. An appropriate value for the duration is the time of concentration (tc) as it is used in the rational method, however, tc is highly sensitive to the catchment size and shape and can vary from one catchment to another. In this study, an AEP of 1 in 2 (or average recurrence interval (ARI) of 2 years) and a fixed duration of 6 h is used similar to the previous RFFA (Haddad and Rahman 2012; Rahman et al. 2019a). Data for I62 were obtained from the Australian Bureau of Meteorology (BOM) website.

2.3 Mean annual rainfall (MAR)

MAR is considered as one the main and easiest to obtain parameters. MAR does not directly affect flood peaks; however, it has secondary impacts on flood generation. In this study, data for MAR was obtained from the BOM website.

2.4 Shape factor

The shape factor is one of the most important factors in the flood generation process, e.g. the longer catchment has a slower flood response. Rahman et al. (2015) suggested a formula to calculate the shape factor (SF) shown below:

$$\mathrm{SF}=\frac{D}{\sqrt{\mathrm{AREA}}}$$
(1)

where D is the shortest distance between the catchment outlet and catchment centre.

2.5 Mean annual evapotranspiration (MAE)

MAE is one of the most influential characteristics in runoff generation. Even though MAE, like MAR, does not have a direct impact on flood peak it has indirect effects on flood generation, e.g. a higher MAE indicates a drier catchment generally in Australia. MAE is a combination of evaporation and transpiration of water from a catchment and is an indicator of water loss through the catchment vegetation during flood events. Data for MAE were obtained from the BOM website.

2.6 SDEN

Stream density (SDEN) is linked to drainage efficiency. A higher SDEN indicates a quicker flood response i.e. a higher peak flow. SDEN is calculated by the equation below.

$$\mathrm{SDEN}=\frac{{S}_{\mathrm{L}}}{ \mathrm{AREA}}$$
(2)

where SL is the total length of all the streams in a catchment measured on a topographic map with scale of 1:100,000.

2.7 S1085

Mainstream slope (S1085) is one of the most critical predictors in RFFA modelling. The higher the S1085, the quicker the flood response. S1085 can be calculated from the flowing equation.

$$\mathrm{S}1085=\frac{(E2 - E1)}{(0.75 \times L)}$$
(3)

where E2 and E1 are elevations at 0.85 and 0.10 lengths of the mainstream measured from catchment outlet and L is the length of the mainstream.

2.8 Forest

The forested fraction of a catchment (FOREST) is defined as the forested area divided by the total catchment area. Forested area increases infiltration during the rainfall-runoff event and decreases the pace of runoff movement as forest increase catchment roughness factor. Deforestation has led to more flood risk in recent decades and including this factor in the study can reveal the impacts of it in flood events. FOREST area is measured on a topographic map with scale of 1:100,000.

3 Methodology

3.1 Quantile regression technique (QRT)

Quantile regression technique is used to develop a prediction equation by regressing a flood quantile (e.g. Q2: flood peak with 1 in 2 AEP) with a set of predictor variables. The general form of the regression can be expressed as:

$$\mathrm{log}\left({Q}_{\mathrm{T}}\right)={b}_{0}+{b}_{1}\times \mathrm{log}\left({V}_{1}\right)+{b}_{2}\times \mathrm{log}\left({V}_{2}\right)+{b}_{3}\times \mathrm{log}\left({V}_{3}\right)+\dots +{b}_{m}\times \mathrm{log}({V}_{m})$$
(4)

where QT = Flood quantile for the AEP of 1 in T, b0, b1, … are regression coefficients and V1, V2, … are predictor variables.

In this study, regression coefficients are estimated using SPSS software based on the ordinary least squares (OLS) method. In SPSS, a backward variable selection method is adopted. Any predictor variable having a p value of less than or equal to 0.10 is considered to be significant and included in the final regression equation. Initially, regression coefficients are estimated based on 126 model catchments, the developed regression equation is then tested on 55 test catchments as a means of independent validation of the developed prediction equation.

3.2 Index flood method (IFM)

IFM can be expressed as below:

$$ Q_T = X_T \times Q_{{\text{mean}}} $$
(5)

where XT = Growth factor for AEP of 1 in T and Qmean = Mean annual flood, which is the growth factor for IFM.

XT is estimated based on the data of 126 model catchments by taking the median of the individual XT values of the model catchments. A prediction equation for Qmean was developed using regression analysis similar to the QRT method as noted above. The general form of this regression equation is shown below:

$$\mathrm{log}\left({Q}_{\mathrm{mean}}\right)={b}_{0}+{b}_{1}\times \mathrm{log}\left({V}_{1}\right)+{b}_{2}\times \mathrm{log}\left({V}_{2}\right)+{b}_{3}\times \mathrm{log}\left({V}_{3}\right)+\dots +{b}_{m}\times \mathrm{log}({V}_{m})$$
(6)

where Qmean = Mean annual flood used as a growth factor in IFM models, b0, b1, … are regression coefficients, and V1, V2, … are predictor variables.

3.3 Performance measures

The following statistical measures are adopted to evaluate the relative accuracy of the QRT and IFM:

$$\mathrm{RE}=\frac{Q\mathrm{pred}-Q\mathrm{obs}}{Q\mathrm{obs}}\times 100$$
(7)
$$\mathrm{RE}r=\mathrm{median}\,[\mathrm{abs}\left(\mathrm{RE}\right)]$$
(8)
$$\mathrm{MSE}=\mathrm{mean}\,[{\left(Q\mathrm{pred}-Q\mathrm{obs}\right)}^{2}]$$
(9)
$$\mathrm{RMSE}=\sqrt{\mathrm{MSE}}$$
(10)
$$\mathrm{Bias}=\mathrm{mean}\,(Q\mathrm{pred}-Q\mathrm{obs})$$
(11)
$$\mathrm{RBias}=\left[\mathrm{mean}\left(\frac{Q\mathrm{pred}-Q\mathrm{obs}}{Q\mathrm{obs}}\right)\right]\times 100$$
(12)
$$\mathrm{RRMSE}=\frac{\sqrt{\mathrm{mean}\left[{\left(Q\mathrm{pred}-Q\mathrm{obs}\right)}^{2}\right]}}{\mathrm{mean}(Q\mathrm{obs})}$$
(13)
$$\mathrm{RMSNE}=\sqrt{\mathrm{mean}\left[{\left(\frac{Q\mathrm{pred}-Q\mathrm{obs}}{Q\mathrm{obs}}\right)}^{2}\right]}$$
(14)

here QT_obs is at-site flood quantile (e.g. Q2) estimated using LP3 distribution (Bayesian method) as noted above for each of the test catchments; and QT_pred is predicted flood quantiles (e.g. Q2) based on either QRT or IFM for each of the test catchments.

4 Results and discussion

The selected catchments did not form any homogenous regions according to the criteria of Hosking and Wallis (1993). All the proposed regions based on catchment areas and state boundaries exhibited H-values much higher than 1.00 indicating these regions are highly heterogeneous. This finding is similar to previous studies such as Rahman et al. (2020) and Rahman (1997) and Bates et al. (1998).

Table 2 shows important statistics in the development of prediction equations in the QRT and IFM framework. The R2 values for the prediction equations for QRT are in the range of (0.65–0.74) with the smallest value for Q100 and the highest value for Q5. The R2 for the prediction equation for Qmean for IFM is 0.75, which is higher than any of the prediction equation for QRT. Prediction equations for QRT are shown by Eqs. 15–20, and the prediction equation for Qmean for IFM is shown by Eq. 21. As it is seen in Table 2, AREA and I62 have appeared in all the prediction equations, which is similar to previous Australian RFFA studies (Haddad and Rahman 2012; Han et al. 2020; Rahman et al. 2019a). Predictor variables such as SDEN, MAR and MAE are the other important predictors. In IFM, the prediction equation for Qmean includes three predictor variables (ARE, I62 and SDEN) which are the same in QRT for Q5 and Q10. Darbin–Watson statistics range 1.94–2.18 for the QRT prediction equations, which is 2.07 for the prediction equation for Qmean for IFM. These values are not far away from 2.00 indicating that the predictor variables in Eqs. 15–21 are not highly correlated. Regional growth factors for IFM are exhibited in Table 3. These growth factors are well compared with other RFFA studies, e.g. Zaman et al. (2012) found regional growth factors 6.84 for Q100 which is much higher than this study (5.5), however, it should be noted that Zaman et al. (2012) used data from arid regions of Australia whereas we have used data from coastal regions of Australia.

Table 2 Summary of important statistics for the prediction equations in QRT and IFM
Full size table
Table 3 Growth factors for IFM
Full size table

Finally, selected prediction equations for QRT are presented below.

$$\mathrm{log}({Q}_{2})=-4.404+0.708\times \mathrm{log}(\mathrm{AREA})+1.452\times \mathrm{log}(\mathrm{I}62)+0.648\times \mathrm{log}(\mathrm{MAR})+0.379\times \mathrm{log}(\mathrm{SDEN})$$
(15)
$$\mathrm{log}({\mathrm{Q}}_{5})=-2.845+0.703\times \mathrm{log}(\mathrm{AREA})+1.938\times \mathrm{log}(\mathrm{I}62)+1.938\times \mathrm{log}(\mathrm{SDEN})$$
(16)
$$\mathrm{log}({\mathrm{Q}}_{10})=-2.822+0.712\times \mathrm{log}(\mathrm{AREA})+2.025\times \mathrm{log}(\mathrm{I}62)+0.406\times \mathrm{log}(\mathrm{SDEN})$$
(17)
$$\mathrm{log}\left({\mathrm{Q}}_{20}\right)=-2.084+0.710\times \mathrm{log}\left(\mathrm{AREA}\right)+2.507\times \mathrm{log}\left(\mathrm{I}62\right)+0.451\times \mathrm{log}\left(\mathrm{MAR}\right)+0.389\times \mathrm{log}(\mathrm{SDEN})$$
(18)
$$\mathrm{log}\left({\mathrm{Q}}_{50}\right)=-1.836+0.715\times \mathrm{log}\left(\mathrm{AREA}\right)+2.829\times \mathrm{log}\left(\mathrm{I}62\right)-0.657\times \mathrm{log}\left(\mathrm{MAR}\right)+0.397\times \mathrm{log}(\mathrm{SDEN})$$
(19)
$$\mathrm{log}\left({\mathrm{Q}}_{100}\right)=-8.001+0.692\times \mathrm{log}\left(\mathrm{AREA}\right)+2.685\times \mathrm{log}\left(\mathrm{I}62\right)-0.731\times \mathrm{log}\left(\mathrm{MAR}\right)+2.260\times \mathrm{log}(\mathrm{MAE})$$
(20)

Prediction equation for Qmean for IFM:

$$\mathrm{log}({Q}_{\mathrm{mean}})=-3.207+0.702\times \mathrm{log}(\mathrm{AREA})+2.053\times \mathrm{log}(I62)+0.358\times \mathrm{log}(\mathrm{SDEN})$$
(21)

Table 3 shows the regional growth factors for the IFM model with different AEPs. Each regional growth factor generates a new value for QT_pred for different AEPs.

$${Q}_{T}\_\mathrm{pred}={X}_{T}\times {Q}_{\mathrm{mean}}$$
(22)

Figures 2 and 3 show the regression standardized residual for Q10 as an example for QRT and Qmean for IFM, respectively. As it can be seen from these figures, standardized residuals are near normally distributed, 90% of the values fall in between ± 2.00, which indicates that the developed regression equations largely satisfied least square model assumptions.

Fig. 2
figure 2

Plot of standardized residual for Q10 for QRT

Full size image
Fig. 3
figure 3

Plot of standardized residual for Qmean for IFM

Full size image

As it is seen in Fig. 4, the median RE values (represented by thick line within the box) mostly match with 0.00–0.00 reference line, with the best results for Q5, Q10 and Q50 for QRT, and Q2, Q5 and Q10 for IFM. There is a slight negative bias for Q2, and a positive bias for Q20 and Q100 for QRT. However, for IFM there is a slight negative bias for Q20, Q50 and Q100 (Fig. 4). The smallest box width (which is an indication of model uncertainty) for QRT is seen for Q5 followed by Q10, Q20, Q50, Q2 and Q100. For IFM, the smallest box width is seen for Q5 followed by Q10, Q20, Q50, Q100 and Q2. For both the QRT and IFM methods, there are few catchments with gross overestimation as can be seen by the outlier points in Fig. 4.

Fig. 4
figure 4

Boxplots of RE values for QRT and IFM

Full size image

As it is seen in Fig. 5, QRT is quite different from IFM in all aspects except the midrange return periods, where both models perform reasonably well for AEPs of 1 in 5 and 1 in 10.

Fig. 5
figure 5

Boxplots of QT_pred/QT_obs (QT_Ratio) values for QRT and IFM

Full size image

Table 7 shows the important statistics for validation of QRT and IFM, where we have compared the evaluation statistics such as REr, QT_pred/QT_obs (Median), RRMSE, Bias, RBias and RMSNE. This evaluation method is frequently used to compare RFFA models (Haddad and Rahman 2012; Naghavi and Yu 1995; Rahman et al. 2020). From Table 7, it can be seen that the lowest REr value of IFM is much lower than that of QRT, which indicates that IFM performs better when AEP values are in the higher range. Additionally, when Q2 value is considered, REr of Q2-IFM outperforms REr of Q2-QRT by 10.8%. The performance of QRT gets better with decreasing AEPs, with the best performance for AEP of 1 in 10; however, IFM outperforms QRT by 2.8%. In terms of QT_pred/QT_obs, IFM performs better than QRT for higher AEPs, with the best performance for AEP of 1 in 2 (1.01 for IFM and 0.93 for QRT); however, QRT outperforms IFM for AEP of 1 in 50 by 0.07.

The REr values for QRT and IFM models range 35.58–48.12%, 32.29–46.29%, respectively; similar statistical measures were used by Haddad and Rahman (2011), with REr ranging 13–42%, and Rahman et al. (2020) with REr ranging 33–44%, and Rahman and Rahman (2020) with REr ranging 22–37%.

RRMSE is another important statistics used to evaluate RFFA techniques (Zrinji and Burn 1994). Lower values of RRMSE indicate higher accuracy of a RFFA method. As shown in Table 7, RRMSE ranges 0.75–1.01 for QRT and 0.74–1.12 for IFM. RRMSE is found in other studies to be 0.22–0.53 for IFM and multiple regression methods used by Malekinezhad et al. (2011), and 0.00–0.27 for QRT and PRT by Rahman et al., (2020), and 0.99–5.69 for IFM and multiple regression methods by Mosaffaie (2015). In terms of Bias, QRT and IFM for the AEP of 1 in 2 have the highest values, − 10 and − 5, respectively. The lowest Bias value for QRT is − 48.38 for AEP of 1 in 100, however, the lowest Bias value of − 332.65 is found for IFM with AEP of 1 in 100, which is a sign of gross under-estimation. In terms of RBias, the lowest and the highest values of 31.76% and 57.25%, are found for QRT with AEPs of 1 in 2 and 1 in 100, respectively. Rahman et al. (2020) in their RFFA study with NSW data reported RBias values in the range of 22–75%. In terms of RMSNE, the QRT model has the lowest value of 1.13 for Q2. RMSNE ranges from 1.13 to 2.09 for QRT and 1.24–1.95 for the IFM model. Rahman et al. (2020) reported this statistic in the range of 1.01–3.6.

Figure 9 represents the observed and predicted discharge values for QRT and IFM, where for both, there is an overestimation in the lower and mid-range discharge values. As it can be seen in higher ranges of AEPs like Q2, Q5 and Q10, there is an underestimation; however, in lower ranges of AEPs such as for Q20, Q50 and Q100 the predicted discharge values match quite well with the observed ones for both the QRT and IFM.

Figure 6 shows cumulative percentage of catchments having REr values in given ranges. As it is seen in Fig. 6, for AEP of 1 in 2, for the range of REr values of 0–19%, 20–39% and 40–59%, there are higher proportion of catchments for the IFM as compared to QRT. For AEPs of 1 in 5 and 1 in 10, both IFM and QRT perform very similarly over all the REr ranges. For other AEPs, QRT performs better than or equal to the IFM.

Fig. 6
figure 6

Plot of cumulative percentage of REr for QRT and IFM

Full size image

In Table 4, a comparison between the REr for the ARR RFFA model and QRT and IFM is shown. As it is seen in Table 4, whilst REr values for QRT are ranging from 33.88 to 48.12%, REr values for IFM are slightly smaller (32.29–46.29%); moreover, the REr values for the ARR RFFA model are larger than both the QRT and IFM. RFFA model is based on 558 stations throughout Australia including NSW, Queensland, and Victoria, however, our study is based on 188 stations in NSW and Victoria. Also, ARR RFFA model used a leave one out validation (in contrast to a split-sample validation as adopted in our study) which generally produces a higher model error as this is a more extensive validation procedure.

Table 4 Comparison of absolute REr values between ARR RFFA model and QRT and IFM
Full size table

As shown in Table 5, RE (%) values are compared between the two models (QRT and IFM). Three different qualitative ranges were selected to compare the two models similar to Rahman et al. (2020). For a RE (%) value beyond the ± 60 range, a ‘Poor’ ranking is assigned to the test catchment, a ranking of ‘Good’ is related RE (%) values ranging from − 30– + 30%, and a ‘Fair’ ranking is given for the rest of the test catchments with RE (%) values between − 60– − 30% and + 30–60%. Table 6 compares the QRT and IFM based on QT_pred/QT_obs (ratio) values grouped in three qualitative ranges. A ‘Poor’ ranking is assigned to a test catchment if the ratio value is greater than 2, ‘Good’ ranking if the ratio value falls between 0.80 to 1.3, and ‘Fair’ if the ratio value is in the range of 0.6–0.8 and 1.3–2. Whilst Table 6 shows that QRT performs better than IFM in general, since the number of stations with ‘Poor’ and ‘Fair’ categories are relatively smaller than IFM, it is clear that IFM has a very strong performance in higher AEPs. As it is also seen in Table 6, QRT outperforms IFM in having a greater number of stations with a ‘Good’ ranking.

Table 5 Grouping RE (%) values for QRT and IFM
Full size table
Table 6 Grouping QT_pred/QT_obs (ratio) values for QRT and IFM models
Full size table

Figures 7 and 8 show the spatial distribution of the absolute RE values of the test catchments for Q20 for QRT and IFM. It should be noted that according to our catchment selection criteria, most western catchments in NSW did not meet the criteria, which is why most of the selected catchments in NSW are from the east. As shown by green pins in these figures, the best performing catchments are those with the lowest absolute RE values of ≤ 25. It is also found that QRT performs slightly better than IFM for Q20 since Fig. 8 shows four more green pins than Fig. 7. For both QRT and IFM, the catchments located near the northeast part of NSW demonstrate smaller RE values. Figure 8 shows seven poorly performing catchments that have RE values of ≥ 100; however, six of those are the same catchments as in Fig. 7. In general, in many cases, both models work well in the selected area with low-performance catchments surrounded by very high-performance ones in Figs. 7, 8, and Appendix Figs. 10 and 11. This shows that the IFM and QRT do not show any spatial coherence in terms of poor model performance. Interestingly, same test catchments are performing poorly by both the IFM and QRT. Further investigation is needed to understand why these catchments are performing poorly by these linear RFFA techniques, which is left for future research efforts.

Fig. 7
figure 7

Spatial distribution of RE values for IFM-Q20 for South East Australia

Full size image
Fig. 8
figure 8

Spatial distribution of RE values for QRT-Q20 for South East Australia

Full size image

5 Conclusion

This study compares two common RFFA techniques, QRT and IFM using data from 181 catchments from south-east Australia, where 55 of them selected randomly as independent test catchments. The mean flood prediction model in IFM has R2 of 0.75 using three predictor variables (AREA, I62 and SDEN); however, the prediction equations of the QRT have an average R2 of 0.69 and have three to four predictor variables from AREA, I62, SDEN, MAR and MAE. The data of these predictor variables can be obtained relatively easily and hence the developed IFM and QRT can be applied easily in practice. Based on RE (%) and Qpred/Qobs ratio values, it is found that QRT underestimates the observed floods for the higher range of AEPs. However, IFM produces more accurate predictions for higher AEPs with a slight underestimation in smaller ranges of AEPs. In terms of comparing predicted and observed flood quantiles for IFM and QRT, IFM’s performance is slightly better than QRT. Comparing REr results shows that, in general, IFM produces better outcomes in higher ranges of AEPs, whilst QRT’s performance gets better with decreasing AEP. The REr values for IFM and QRT range 32.29–46.29% and 35.58–48.12%, respectively. There is no spatial coherence in the performance of the IFM and QRT. Most of the poor performing catchments are found to be common in both the IFM and QRT.

Based on REr results, both models have shown a good performance compared to the ARR-RFFA model. The REr values of ARR-RFFA model ranges 57.25–64.06%. It should be noted that our study uses a different data set than ARR in terms of record length and number of stations and validation technique. ARR-RFFA model adopted a leave-one-out validation technique based on 558 Australian catchments and this validation technique is more rigorous than the split-sample validation adopted in this study, which is the possible reason for having higher REr values for ARR-RFFA model. It is expected that the new methods proposed here will be accepted in the next version of ARR.

Further study should focus on extending the adopted methodology to all the Australian states, apply leave-one-out and Monte Carlo cross-validation techniques and incorporating the impacts of climate change on design flood estimates using QRT and IFM.