1 Introduction

Risk is a function of seismic hazard, exposure, and vulnerability (Algermissen 2007). The total risk is defined by the following relation (Sinadinovski et al. 2005):

$$\begin{aligned} {\text {Risk}} = {\text {Hazard}} \times {\text {Elements}}\,{\text {at}}\,{\text {Risk}} \times {\text {Vulnerability}}\,{\text {of}}\,{\text {the}}\,{\text {Elements}}\,{\text {at}}\,{\text {Risk}}\end{aligned}$$
(1)

A seismic hazard is a natural process or physical phenomenon often related to earthquakes and may cause loss of life, injury or property damage. Additionally, such events can cause environmental damage or social and economic disruptions (UNISDR 2009). Measures of exposure can be based on the number of people affected or the types of resources in a region (UNISDR 2009). Elements at risk are those directly influenced by earthquake hazards (Sinadinovski et al. 2005). Vulnerability is often broadly used to include element exposure (UNISDR 2009) . Earthquake vulnerability models are used to estimate the level of damage caused by a given level of ground shaking for a wide range of building types (Sinadinovski et al. 2005). Recently, many studies on seismic hazards and risks have been performed in different parts of the world (e.g., (Simeonova et al. 2006; Leydecker et al. 2008; Pavel et al. 2016; Valentini et al. 2017); (Loi et al. 2018; Solakov et al. 2019a; Mahmood et al. 2020)). Other studies, such as (Tyagunov et al. 2006), (Zhu et al. 2016), (Mesgar and Jalilvand 2017), (Solakov et al. 2019b), (Derakhshan et al. 2020) and (Kolathayar 2021) expanded their research by considering population exposure.The present study is an earthquake risk scenario analysis of the city of Plovdiv (Fig. 1), one of the largest earthquake-prone cities in Bulgaria.

Fig. 1
figure 1

Administrative zoning (suburbs) in the city of Plovdiv and its location in the territory of Bulgaria

Full size image

The history of the city of Plovdiv spans over 6,000 years, with traces of a Neolithic settlement dating to approximately 4000 BC. In 342 BC, it was conquered by Philip II of Macedon, the father of Alexander the Great, who renamed it “Philippopolis” or “the city of Philip” in his own honor. In 72 AD, it was incorporated into the Roman Empire, where it was called Trimontium (City of Three Hills) and served as the metropolis (capital) of the province of Thrace. In the Middle Ages, it retained its strategic regional importance, changing hands between the Byzantine and Bulgarian Empires. It came under Ottoman rule in the 14th century. In 1885, Plovdiv became part of Bulgaria with the unification of that region and the Principality of Bulgaria. At present, Plovdiv is one of the largest industrial and cultural regions in Bulgaria, with a population of more than 340,000 people. Currently, studies of seismic hazard have been performed for some of the largest cities in Bulgaria based on the methodology for developing ground motion hazard maps (earthquake scenarios) that was adopted in the Risk EU Project (2001–2004) funded by The European Economic Commission (Contract: EVK4-CT- 2000-00014) Faccioli et al. (2003). Deterministic earthquake scenarios have been generated for several cities in Bulgaria: Blagoevgrad Solakov et al. (2020a)), Ruse Solakov et al. (2020b), Plovdiv Solakov et al. (2021a) and Veliko Tarnovo Solakov et al. (2021b). Both deterministic and probabilistic earthquake (seismic) ground-motion scenarios for the cities of Sofia Solakov and Simeonova (2006), Ruse Solakov et al. (2021c) and Veliko Tarnovo Solakov et al. (2023), were assessed.

Here presented scenarios (deterministic and probabilistic) are generated using the methodology adopted in the Risk EU Project (Contract: EVK4-CT-2000-0001). The approach applied for the creation of ground motion maps combines via GIS, source geometry, an earthquake occurrence model, maximum earthquake magnitude and appropriate attenuation relations for shallow (crustal) earthquakes. Additionally, an assessment of the base level of the seismic risk considering population (human) exposure in the territory of the city of Plovdiv is performed. Population exposure refers to the population present within the hazard area that would be directly affected by a potential earthquake (Freire and Aubrecht 2012).

2 Seismotectonics

In the Eastern Mediterranean, active geodynamic processes are basically influenced by three large plates (African, Arabian and Eurasian) and several minor ones (Anatolia, Sinai, Aegean and Adria). This area is currently undergoing a widespread regional extension, which can be dated back to the Eocene–Early Miocene Gautier et al. (1999). There is a common agreement in the literature (as, for example, in Jackson and McKenzie (1988), Papazahos et al. (2000) and ten Veen et al. (2004)) on this general geodynamic framework, that the African plate is undergoing the Eurasian one and that there is a left lateral transtension between the Arabian and African plate.

The collision of the Arabian and African plates with the Eurasian is an important element of the tectonic background of the Balkan Peninsula. In the Balkan Peninsula, the NS extension observed in Northern Greece and the Aegean Sea continues at 5 mm/y into the inner Balkans Burchfiel et al. (2006). Bulgaria is located at the northern boundary of the Aegean extensional regime (in Burchfiel et al. (2006) and Kotzev et al. (2006)). The current tectonics of Bulgaria are defined by the processes of extension in a general north–south direction. Consequently, the active fault structures are striking from east–west and southeast–northwest (in Burchfiel et al. (2006) and Kotzev et al. (2006)).

It is accepted (in Métois et al. (2015), among others) that the central and western parts of the southern Bulgaria are located in the transition zone between the Eurasian continental plate and Aegean microplate—South Balkan extensional region. Analyses of the horizontal velocities (Georgiev et al. 2011) have indicated an increase from 2 mm/y in the central part of southwestern Bulgaria till to 10 mm/y in the Khalkidhiki Peninsula (Greece).

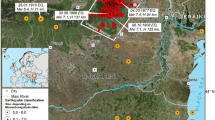
The regional seismotectonic pattern is illustrated in Fig. 2, which is also the epicenter map of historical and instrumental recent earthquakes that have occurred in the Plovdiv region. The figure also shows the model of the active faults in the region that is defined in European project SHARE (Seismic Hazard Harmonization in Europe, (Basili et al. 2013)). The seismogenic potential of the faults, as defined in Basili et al. (2013), was considered in during the scenario generation.

Fig. 2
figure 2

Spatial pattern of seismicity (historical and recent earthquakes with \(M_{W}>3.0\)) and active faults for the city of Plovdiv and the surrounding area (modified from Solakov et al. (2021))

Full size image

The seismic history of the city of Plovdiv includes 1928 earthquakes, such as the \(M_{W}6.5\) foreshock on April 14, 1928, and the main \(M_{W}7.1\) event on April 18, 1928, which caused the strongest seismic effects ever observed in Plovdiv Kirov (1945). Pronounced surface ruptures occurred during the \(M_{W}7.1\) earthquake Yankov (1935). The two earthquakes completely destroyed 74,000 buildings in Plovdiv, Chirpan and Parvomay (DIPOZE 1931).

3 Soil properties

The soil properties in the study area were determined based on the average shear-wave velocity in the upper 30 m of the soil/rock profile - \(V_{s30}\). The \(V_{s30}\) values for the city of Plovdiv (illustrated in Fig. 4) are based on the results presented in Rangelov et al. (2020) and supplemented with data from the USGS slope-based global model (available at https://earthquake.usgs.gov/data/Vs30) in order to cover the built-up area of the city.

Most of the territory of the city of Plovdiv is characterized by velocities in the range of 200–250 m/s. The lowest values (between 180 and less than 200 m/s) are observed along the Maritsa River, which crosses the northern part of the city in a subequatorial direction. The \(V_{s30}\) values are larger than 350 m/s in the areas of the seven syenite hills that are located in the central part of the city (Fig. 3).

Fig. 3
figure 3

Average shear-wave velocity in the upper 30 m of the soil/rock profile in the Plovdiv region (modified from Solakov et al. (2021a))

Full size image

4 Ground motion attenuation (GMPE‘S)

An essential element in both deterministic and probabilistic seismic hazard analyses is the ability to estimate strong ground motion from a specified set of seismological parameters. This estimation is carried out using a ground motion prediction equation, or what is also commonly referred to as GMPEs, also referred to as attenuation models. A GMPE is a mathematical equation that relates a given strong-motion parameter to one or more parameters of the earthquake source, wave propagation path and local site conditions, collectively referred to as seismological parameters. Selection of the ground motion prediction equations (GMPE’s, also referred to as attenuation relations or models) is an essential step in seismic hazard assessment. The relations between some strong motion parameters and earthquake rupture parameters, wave propagation paths and local site conditions are represented with mathematical equations, such as GMPE’s.

The selection process of adequate GMPEs started from a list of available ground motion models to which a set of exclusion criteria (presented in Cotton et al. (2006) and Bommer et al. (2010)) related to tectonic settings, the characteristics of basic data sets, the frequency ranges of prediction equations, and other factors were applied. The details of the selection process and justifications for selecting certain equations are described in Solakov et al. (2019a) and Solakov et al. (2019c). Finally, the following six ground-motion models for tectonically active regions were selected: AS14 Abrahamson et al. (2014), AB14 Akkar et al. (2014), BA14 Boore et al. (2014), CB14 Campbell and Bozorgnia (2014), CY14 Chiou and Youngs (2014), and CF15 Cauzzi et al. (2015).

The method presented in Scherbaum et al. (2009) was chosen to test the selected 6 models against real ground-motion data from the Balkan countries, Italy and countries in the Middle East. The data used are from the Engineering Strong Motion (ESM) data base presented in Luzi et al. (2016). The fit between the observed data and model results is given by the following relation Scherbaum et al. (2009):

$$\begin{aligned} {\text {LLH}} = - \frac{1}{N}\sum \limits _{{i = 1}}^{N} {\log _{2} \left( {g\left( {x_{i} } \right) } \right) }. \end{aligned}$$
(2)

where N is the number of observations \(x_{i}\) and g is the probability density function predicted by the GMPEs (normal distribution). A small LLH value (ranking criterion) indicates that the candidate model is highly similar to the observation model. The approach presented in Delavaud et al. (2012) was used to weight the selected GMPEs. The weights of the selected six GMPEs (presented in Table 1) are used in the probabilistic earthquake scenarios.

Table 1 Weights of the selected GMPE’s used in the computation
Full size table

5 Deterministic earthquake scenarios for the city of Plovdiv

By deterministic scenario it is mined, a representation of the severity of ground shaking over the studied urban area using one or more hazard descriptors. The basic characteristic of the approach is that a deterministic scenario should be consistent with the regional seismotectonics, the seismic history of the city and the active faults that generate earthquakes and have the largest influence on the considered urban area.

The PGA scenario for the city of Plovdiv is mapped in Fig. 4. The corresponding event is the \(M_{W}7.1\) earthquake that occurred at the active fault located north of the city of Plovdiv (Fig. 2). The ground motion in the city is estimated based on the application of the selected 6 GMPEs for shallow (crustal) earthquakes. The ground motions in PGA are calculated as follows:

$$\begin{aligned} {\text {GM}}(x,y) = \sum \limits _{{i = 1}}^{6} {w_{i} g_{i} (x,y)} \end{aligned}$$
(3)

where GM(x, y) is the evaluated ground motion at point with coordinates (x, y), \(g_{i}(x,y)\) is the median ground motion predicted by \(i^{th}\) GMPE and \(w_{i}\) is the corresponding weight.

The PGA values vary between 0.19 and 0.44 g throughout the city. The lowest values of 0.19 g are observed near the seven syenite hills located in the central part of the city.

Fig. 4
figure 4

Deterministic earthquake scenario for the city of Plovdiv based on PGA (modified from Solakov et al. (2021b))

Full size image

6 Probabilistic seismic hazard assessment for the city of Plovdiv

The probabilistic seismic hazard level corresponds to the probability that various levels of strong ground motion will be exceeded during a specific period at a given site. The ground motion levels may be expressed in terms of peak ground acceleration (velocity and displacement) and/or peak spectral response amplitudes for a range of frequencies.

Estimation of probabilistic seismic hazard for a region is one the most important challenges in the field of seismology. The probabilistic approach (PSHA) was developed in the late 1960 and early 1970 at the Universidad Nacional Autonoma de Mexico (UNAM) and the Massachusetts Institute of Technology (MIT) to provide a systematic method to deal with the uncertainty in the numbers, sizes, and locations of future earthquakes (Cornell 1968) than compared to the arbitrary selections used previously (Bommer and Abrahamson 2006). Currently, the PSHA is the most widely used approach for estimating seismic-design loads. It is assumed that the seismic hazard at a considered site is defined by integrating the effects of ground motion from earthquakes of different sizes occurring at different locations within different seismic source regions and with different frequencies of occurrence (Thenhause and Campbell 2003). In our study, the PSHA is estimated implemented by using a version of the machine code EQRISK (McGuire 1976) that was developed in Bulgaria and has been used in practice for probabilistic hazard assessment in Bulgaria (presented in Solakov et al. (2019)).

6.1 Seismic source model

An important element of seismic hazard assessment is the design of a seismic source model, which demands translating seismotectonic information in to a spatial approximation of earthquake location and recurrence. The connection between the collected database and seismic source model is a regional seismotectonic map (model). The seismotectonic model is based on coherent merging of the total regional neotectonic, geophysical and seismological data bases and concerns the results of previous investigations. The seismotectonic model allows geological, geophysical and seismological evidence to be combined aiming to obtain an overall understanding of earthquake generation. A seismic source model is a simplification of regional seismotectonic model into a form that can readily be employed for hazard computation (Thenhause and Campbell 2003)).

In the present study, a seismic source model with 19 seismic sources that are located in the 200 km region surrounding the city of Plovdiv is defined. The model contains all seismic sources that significantly affect the seismic hazard level for the city of Plovdiv. For each seismic source, the geometry, active fault parameters, earthquake distribution within the source area, earthquake recurrence frequency and maximum potential earthquake magnitude are defined. The seismic source model used in seismic hazard analysis for the city of Plovdiv is illustrated in Fig. 5 and specified in Table 2.

Fig. 5
figure 5

Seismic source model (modified from Solakov et al. (2019))

Full size image
Table 2 Seismic source parameters used in the hazard analysis
Full size table

6.2 Seismicity parameters

The seismicity parameters (presented in Table 2) are determined based on the magnitude-frequency relation with the annual seismic rate parameter \(\lambda\) (number of earthquakes with magnitudes between \(M_{min}\) and \(M_{max}\)), the b-value in the Gutenberg-Richter Gutenberg and Richter (1944)) exponential relation, the minimum magnitude \(M_{min}\) and the maximum possible magnitude \(M_{max}\). The seismicity parameters for each seismic source in the area within a radius of 200 km surrounding the studied city and used in the seismic hazard analysis are estimated and presented in Solakov et al. (2019a). For the purpose of the seismological study a catalog for the region bordered by 41.0\(^{\circ }\) \(-\)44.6\(^{\circ }\)N and 22.0\(^{\circ }\) - 30.0\(^{\circ }\)E was compiled. The earthquake catalog includes 1062 shallow (crustal) earthquakes with magnitude \(M_{W}>3.0\). The catalog is processed in the sense that duplicated events are removed, and the foreshocks and aftershocks are identified. Uniform magnitude measure is estimated for earthquakes. To examine the completeness of the catalog data two tests that are presented in Stepp (1971) and Hakkimhashemi and Grüntal (2012) are applied. The results show that 475 years for magnitude \(M_{W}\) larger than or equal to 6.0 (\(M_{W}\ge 6.0\)), 167 years for earthquake with magnitude estimates in the interval (4.5\(-\)6.0), and 37 years for magnitude \(M_{W}<4.5\). Seismicity parameters a, b and \(M_{max}\) are considered in the PSHA Logic tree.

6.3 Treatment of uncertainties

Handling uncertainties is a key element of probabilistic seismic hazard analysis. Two types of uncertainty are defined in seismic hazard analysis-random and modeling (McGuire 1993). Distinction between the two types of uncertainty has emerged as an important issue in the proper estimation of seismic hazard. The first type uncertainty (aleatory) represents the randomness inherent in the natural phenomena of earthquake generation and seismic wave propagation. Aleatory variability is included directly in the PSHA calculations by means of mathematical formulation.

Modeling (epistemic) uncertainties come from statistical or modeling variations. The large uncertainties in seismic hazard result from lack of knowledge about earthquake cause, characteristics, ground motions, i.e. from uncertainties in the inputs. There are many epistemic uncertainties in any seismic hazard assessment, including the configuration and characteristics of the seismic source zones, the model for earthquake recurrence frequency, and the maximum earthquake magnitude.

In the PSHA, the established procedure is to incorporate the epistemic uncertainty into the calculation through the use of logic tree. Logic tree was first introduced into PSHA by Kulkarni et al. (1984) as a tool to model and quantify the uncertainties in the inputs required for such analysis and have since become a part of PSHA Coppersmith and Youngs (1986). The logic tree allows a formal characterization of uncertainty in the analysis by explicitly including alternative interpretations, models, and parameters that are weighted in the analysis according to their probability of being correct.

In the present study, to account for the epistemic uncertainties in seismic input, a logic tree approach is used in the seismic hazard assessment of the city of Plovdiv. To propagate the epistemic uncertainties through the probabilistic seismic hazard, a logic tree presented in details in Solakov et al. (2019a) is used in the study.

7 Probabilistic ground motion scenarios for the city of Plovdiv

Using the model of seismic sources illustrated in Fig. 5 and defined in Table 2, probabilistic seismic analysis (PSHA) for the city of Plovdiv is performed. The ground motion values (in [g]) are calculated using the six selected GMPE’s for crustal earthquakes. The epistemic uncertainties are considered, with 4-level logic trees generated for each seismic source. Probabilistic scenario maps are created in terms of PGA for 475- and 1000-year return periods.

Fig. 6
figure 6

Probabilistic earthquake scenario for the city of Plovdiv in terms of PGA for a 475-year return period

Full size image

The estimated PGA for the city of Plovdiv varies from 0.20 \(-\)0.34 g and 0.29\(-\)0.46 g for the 475- and 1000-year return periods, respectively (as shown in Figs. 6 and 7 and Table 3). As shown in Table 3, the highest deterministic estimates of PGA coincide with the highest probabilities ones for 1000-year return period. Moreover, the deterministic estimates indicate that the probabilistic results are reasonable.

Table 3 Seismic hazard estimates
Full size table
Fig. 7
figure 7

Probabilistic earthquake scenario for the city of Plovdiv in terms of PGA for a 1000-year return period

Full size image

8 Population exposure

The earthquake risk for Plovdiv was assessed considering the earthquake hazard level, the population (human) exposure as an element at risk, and the vulnerability of elements to ground shaking. The three factors that influence the seismic risk follow the multiplicative rule, as described in Dao and Peduzzi (2003). Theoretically, if no-one lives in an area exposed to a hazard and if the population is invulnerable, the risk is correspondingly \({\varnothing }\) (null).

We model the population exposure by considering the seismic hazard and population in a given target area. Similar to Solakov et al. (2019), we introduce a quality parameter called the population exposure index (PEI) with five classes: minor, low, moderate, high and major. Their number and range were carefully selected and evaluated according to several criteria, such as the optimum number of levels for visual representation and the levels of errors. The combination of seismic hazard and population density information can be used to estimate population exposure as an element of risk. A hypothesis is established: Similar to the risk, the expression of the PEI can be simplified as a multiplicative formula:

$$\begin{aligned} {\text {Pop}}\,{\text {Exp}}^{E} = H^{E}.\,{\text {Pop}}^{E} \end{aligned}$$
(4)

where \(PopExp^{E}\) is the population exposure for a single spatial element E, which here is the site (polygon) of an individual building, and \(H^{E}\) and \(Pop^{E}\) are the seismic hazard classes and are determined according to the levels in Table 4 and Table 5, respectively.

Table 4 Seismic hazard levels
Full size table
Table 5 Population density levels
Full size table

The input data used for the analysis are 1) seismic hazard data (deterministic and probabilistic, displayed in Fig. 4 and 6) for the territory of Plovdiv and 2) the population distribution based on the total number of citizens reported by the National Statistical Institute (NSI) in 2020 (available at https://infostat.nsi.bg/infostat/pages/external/login.jsf); moreover, built-up land information released by the Geodesy, Cartography and Cadastre Agency of Bulgaria (GCCA) is used.

For consistency, the seismic hazard levels are the same as those in Solakov et al. (2019b), in which calculations were performed over the entire territory of Bulgaria. The seismic hazard levels obtained for the examined city fall within the highest classes in Table 3. From both scenarios, almost the entire territory is classified as level 5, with the exception of the farthest southwestern parts of the city and the seven syenite hill areas in the central part of the city. Our database includes the resident population (i.e., the night-time population) published by the NSI, and spatiotemporal variations in the population distribution in the urban area are not considered. According to the data, the total population living in the city of Plovdiv in 2020 was 342,028 people. In the calculations, we used the population per 100 square meters [pers./100 m2 ] obtained for the site of each residential building in the city. The results vary widely from 1.9 to 42.8 persons/100 m2, with an average of 6 and a median of 4 persons/100 m2.

There are 25,987 residential buildings in the city of Plovdiv according to the data from the GCCA. Table 6 presents the distribution of residential buildings based on the number of floors and floor area in m2 . Most buildings 67% are low-rise buildings with up to 3 floors. These are the homes of 15% of residents. Additionally, 247 buildings (1%) with more than 10 floors are inhabited by 9% of the people in the city. The seismic hazard level and population density were estimated at every site (polygon) and for each individual building according to the levels in Table 4 and Table 5 using GIS.

Table 6 Distribution of buildings (based on the number of floors and TFA) in Plovdiv
Full size table

Equation 4 is applied to obtain the population exposure for all individual spatial elements (building sites). The obtained results are categorized into the same five classes, namely minor, low, moderate, high and major, using the standard risk matrix (see, e.g.,http://jasonpope.co.uk/risk-management/) displayed in Fig. 8.

Fig. 8
figure 8

The standard risk matrix used for PEI classification

Full size image

Calculations were performed for two seismic scenarios: one deterministic scenario (an earthquake with magnitude \(M_{W}7.1\) in the active fault located north of the city; Fig. 4) and one probabilistic scenario (for a 475-year return period, as described above; Fig. 6). The obtained results are presented in Table 7 and Fig. 9 and Fig. 10, respectively. The PEI values obtained for the deterministic scenario vary from low to major. Only 4% (1026 residential buildings) of sites have PEI values classified as low (Table 7). These sites are associated with one-story houses located in the central part of the city near the syenite hills and to the southeast. The sites for which moderate and high values are obtained account for approximately 35% of all sites. A quarter, or 25%, of sites are characterized by major exposure index values. These sites are marked in red in Fig. 9 and are concentrated near the periphery of the central part of the city, in the eastern suburbs of Trakia and Izgrev and in areas with tall buildings north of the river. Notably, 76.3% of the population of Plovdiv lives in these areas. Figure 10 presents the PEI obtained for the probabilistic earthquake scenario (for a 475-year return period) with the same categories, and similar results were obtained (see Table 7). The main differences in results are as follows: 1) the number of buildings and portion of the population classified as low exposure risk are concentrated in the central part of the city only, and 2) the percentages of sites in the major and high classes slightly increased.

Table 7 Distribution of buildings and the population in the obtained PEI classes for the city of Plovdiv
Full size table
Fig. 9
figure 9

Population exposure index (PEI) obtained from the deterministic scenario for the city of Plovdiv

Full size image

In both cases (deterministic and probabilistic), the PEI results indicate that 96% of the population in Plovdiv is exposed to high seismic hazard levels. The largest number of residential building at high risk is in the area north of the Maritsa River and in the Trakia and Vastanicheski districts. Because only residential buildings were included in our analysis, the industrial zones of Plovdiv, which are colored in gray on the maps, are areas with high concentrations of people during working hours each day.

Fig. 10
figure 10

PEI obtained from the probabilistic scenario (475-year return period) for the city of Plovdiv

Full size image

9 Results and conclusions

Our study shows that an earthquake near the city of Plovdiv can generate a significant number of casualties within a short period of time. Based on both deterministic (DSHA) and probabilistic (PSHA) earthquake scenarios (in PGA) generated for the city of Plovdiv, we found that most of the city’s territory can be classified at the highest level of seismic hazard at a PGA of 0.26.

The average population density per square meter of building floor area is 0.0195. More than half of the population lives in buildings with more than seven floors, and almost one-tenth of the population lives in buildings with more than 10 floors.

The exposure data, combined with the evaluated hazard levels, were used to establish the PEI over the considered territory. For the 25% of the study area that is inhabited by more than 75% of the city’s residents, the maximum PEI classification is obtained. The integrated GIS results that are presented can contribute to the development of GIS applications and digital maps that are needed as the bases for evaluating the vulnerability of the region to earthquake hazards and preparing for events.

In conclusion, seismic risk assessments of cities provide valuable information for enhancing seismic safety and mitigating disasters.