Abstract
Flood is one of the most common natural disasters, which also triggers other natural disasters such as erosion and landslides. Flood damage can be minimised by ensuring optimum design of drainage infrastructure and other flood management tasks, which depends largely on reliable estimation of flood quantiles. This study investigates flood quantile estimation in ungauged catchments using a kriging-based regional flood frequency analysis (RFFA) technique. Three main research objectives are addressed in this study. Firstly, kriging-based RFFA models are developed using 558 catchments from eastern Australia in the range of frequent to rare flood quantiles (2, 5, 10, 20, 50 and 100 years of average recurrence intervals (ARIs)). Secondly, a validation of the models by adopting a leave-one-out (LOO) validation technique is undertaken to identify the best and the worst performing catchments across eastern Australia. Finally, a detailed comparison is made for the kriging-based RFFA technique with a generalised least-squares-based quantile regression technique, known as ‘RFFE model 2016’ using the same dataset to evaluate whether there are general patterns of the performance in different catchments. The study shows that for eastern Australia (a) the developed kriging-based RFFA model is a viable alternative for flood quantile estimation in ungauged catchments, (b) the 10-year ARI model Q10 performs best among the six quantiles, which is followed by the models Q5 and Q20, and (c) the kriging-based RFFA model is found to outperform the ‘RFFE model 2016’.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Flood-related economic losses and number of fatalities have increased dramatically over the past decades around the globe (OECD 2016; CRED and UNISDR 2015). Floods damage crops, livestock, properties and infrastructure, and also negatively impact ecology by increasing erosion and pollution of rivers. An optimum design of drainage infrastructure can reduce the damage, which depends largely on a reliable estimation of flood quantiles—defined as the flood discharge associated with a given return period or average recurrence interval (ARI) (Kuczera and Franks 2019; Rahman et al. 2019). The most direct method for flood quantile estimation is flood frequency analysis (FFA), which requires a long period of recorded streamflow data at the site of interest. In such situations, where streamflow data are not available, regional flood frequency analysis (RFFA) is adopted, which attempts to exploit flood data available within the region by the use of flood information from nearby or similar gauged catchments (Stedinger et al. 1993; Ouarda et al. 2001; Haddad et al. 2013). The technique primarily regionalises flood data, which are assumed to be independent (in both space and time), identically distributed, not to be affected by natural or manmade changes (Cunnane 1989; Ouarda et al. 2001; Haddad and Rahman 2020); then, use predictor variables, such as catchment physiographic, geomorphologic or climatic characteristics, to estimate the streamflow for a given catchment. The limitation of using these approaches (whether FFA or RFFA) is that the requirement of a reasonably long period of flow observations collected at or (at least) close to the site of interest. Additionally, these approaches assume that the flow data are stationary over time, which may not always be the case especially in the context of climate change and land use changes (Ishak and Rahman 2019).
RFFA has a long history in hydrology for being used in flood quantile estimation, and accordingly, the last couple of decades, in particular, have seen extensive research on RFFA techniques worldwide. RFFA is a broad area of study depending on the diversity of climatic conditions and site characteristics in general; hence, different researchers have focused on different issues (Micevski et al. 2015). In the 1970s and early 1980s, the focus was on developing reliable at-site FFA techniques, while in the late 1980s the attention was shifted towards developing new and improved RFFA techniques (e.g. Potter 1987; Kirby and Moss 1987; Cunnane 1988; and NRC 1988). Some studies (Potter and Lettenmaier 1990; Bobee et al. 1993) in early 1990s suggested to compare the existing RFFA techniques and to look for an improvement as an alternative for developing new methods. During the next twenty years, researchers had made efforts to develop techniques in which similarity between sites is defined by a multidimensional space of catchment or statistical characteristics (Douglas 1995). Alternate methods were also derived so that each site has its own region, for instance, the region of influence (ROI) approach (Burn 1990a and 1990b) and canonical correlation analysis (Cavadias 1990). In 2003, the International Association of Hydrological Sciences launched a collective effort, known as the Prediction in Ungauged Basins (PUB) initiative, to improve the knowledge of climatic as well as landscape controls on hydrological practices and to improve the ability to estimate the water fluxes in ungauged catchments associated with their uncertainties (Sivapalan et al. 2003). One of the significant tasks that the PUB initiative attained was performing the comparative evaluation of different modelling approaches in terms of time/space scales, climate, data requirements and type of application (Parajka et al. 2013).
In the last two decades, with the advent of geographical information systems, alternative methods of using the flood quantiles directly in regressions against catchment characteristics (Griffis and Stedinger 2007; Engeland and Hisdal 2009) or geostatistical methods that exploit the spatial correlation of floods either in space (Merz and Bl¨oschl 2005; Merz et al. 2008) or along the stream network (Skøien et al. 2006; Laaha et al. 2012) have become popular. One of the strengths of the geostatistical techniques is that it directly exploits the spatial correlations of the flood data to develop regional maps of the predicted variables; there is no need for defining pooling groups explicitly, but a relatively dense stream gauge network is needed in general (Chokmani and Ouarda 2004; Parajka et al. 2013; Salinas et al. 2013). Geostatistical maps of hydrological variables are often produced using an interpolation technique like kriging, a model established originally in the mining industry (Skøien et al. 2006). In a typical kriging model, the hydrologic variable (that is predicted) is considered to be spatially continuous and the prediction equations are made based on the geospatial locations.
Various types of kriging models are used in hydrology, such as ordinary kriging (Adhikary et al. 2016; Farmer 2016), canonical kriging or co-kriging (Ouarda et al. 2001; Chokmani and Ouarda 2004), topological kriging or ‘top-kriging’ (Skøien et al. 2006; Skøien and Blöschl 2007; Persiano et al. 2021) and kriging with an external drift (KED) (Goovaerts 2000). In a number of studies emphasising on the prediction of mean annual runoff (Skøien et al. 2006) and other variables of the streamflow distribution (Castiglioni et al. 2011; Archfield et al. 2013; Viglione et al. 2013), top-kriging has been found to be performing better than many other kriging types, including ordinary kriging (Sauquet 2006). However, ordinary kriging is the simplest type of kriging model that is capable of combining flood quantile at multiple sites for making regional prediction. It provides a competitive first-order approximation and hence is better understood than top-kriging or other types of kriging. It is also hypothesised by many researchers that a simple geostatistical method can produce estimates nearly as good as it is produced by more advanced geostatistical methods. Farmer (2016) explored to characterise the spatial correlation of daily streamflow data in Southeastern US and showed that the ordinary kriging model can generate accurate streamflow predictions at ungauged sites, significantly outperforming more traditional approaches that employ a single-index stream gauge. Adhikary et al. (2016) applied ordinary kriging model for spatial interpolation of monthly and mean annual rainfall (MAR) to produce the gridded rainfall dataset for the Middle Yarra River catchment in Australia, then compared the result with a deterministic interpolation method and found that the ordinary kriging-based stochastic interpolation method outperformed the deterministic method for spatial interpolation of rainfall.
Valizadeh et al. (2017) reviewed artificial intelligence and geostatistical methods to forecast the runoff at ungauged catchments. For a large dataset of Canadian rivers, Durocher et al. (2019) found that application of generalised additive models (GAM), local regression, thin plate spline and kriging can show the best predictive powers among several other RFFA techniques. Meral and Eroğlu (2021) conducted a flood risk analyses in Bingöl, Eastern Turkey using kriging and weighted sum models. Baidya et al. (2020) compared inverse distance weighing method, ordinary kriging and area weighted method in RFFA data the Mahanadi River basin in India. They noted that at smaller return periods, index flood method is preferable, but for the higher return periods kriging provides more accurate results. In another recent study, Tran and Kim (2022) showed that polynomial chaos kriging and Gaussian process with kriging variance can provide more accurate prediction of the hydrograph and flood peaks.
In Australia, there have been several studies that have focused on several RFFA techniques (both process-based and statistics-based) and ways of minimising errors in flood quantile estimates (e.g. Haddad and Rahman 2012; Haddad et al. 2013; Zaman et al. 2012; Durocher et al. 2018; Rahman et al. 2018; Haddad and Rahman 2019). When reviewing the rich literature on RFFA techniques in Australia, it has been found that there are a very few studies that directly compared the different RFFA methods. The predictive performance for ungauged catchments is dependent on the hydrological or climatological setting of the region as well as the quality and the length of the datasets used in developing and testing the technique; this idea possibly made process-based techniques (e.g. rainfall runoff model that has the inclusion of physical catchment characteristics) more popular in Australia. But, in data-rich regions of the world, statistics-based RFFA techniques have been found to perform better in ungauged catchments than other RFFA approaches (Viglione et al. 2013). Also due to the large heterogeneity in Australian catchments, it is often difficult to establish homogeneous regions in Australia (Rahman et al. 2019); hence, a simple geostatistics-based technique like kriging that does not strictly require a homogeneous region, but needs a relatively dense stream gauge network, can be a viable alternative for RFFA in Australia.
In this study, kriging-based RFFA models are developed and tested for eastern Australia (data-rich areas of Australia having highest density of gauging stations) using a comprehensive flood database. This research is particularly topical given the fact that there has been no study on the application of kriging in RFFA problem in Australia. Methods used and developed in this study are therefore centred on the flood quantile estimation in ungauged catchments in the range of frequent to rare ARIs (2, 5, 10, 20, 50 and 100 years). The main innovation of this study is development and testing of kriging in RFFA using a large dataset. It also quantifies the uncertainty associated with the new kriging-based RFFA method. It is expected that the outcome of this study would encourage applying kriging in RFFA instead of more complex techniques.
Various aspects of the streamflow data collation (collated by the Australian Rainfall and Runoff (ARR)-the national guideline (ed. Ball et al. 2019)) are described in Sect. 2. Section 3 discusses thoroughly the mathematical formulations and the theory behind the technique of the development and testing of the kriging-based RFFA models. This section also evaluates the developed models, identifies the best/worst performing catchments in the validation process by adopting a leave-one-out (LOO) validation technique and compares the performance of the kriging-based RFFA technique on a global scale as well as with the currently recommended RFFA technique in ARR 2019, ‘RFFE Model 2016’. Finally, Sect. 4 outlines the main conclusions of this study.
2 Materials and methods
2.1 Study area and data
The study area comprises of 558 unregulated catchments in the eastern coast of Australia (New South Wales (NSW), Victoria (VIC) and Queensland (QLD)). The reason for selecting these three states is that there are a good number of high-quality stream gauging stations in these states that can be used in RFFA study. These catchments have also been used in the development of the ‘RFFE model 2016’ (Rahman et al. 2019); hence, the annual maximum flood (AMF) data series for the selected catchments used in this investigation has been obtained from the project ARR_ RFFE Model 2016 (ed. Ball et al. 2019). The same catchments set is adopted so that the performance of the kriging-based RFFA model can be compared objectively with that of the ‘RFFE model 2016’ (which is covered in Sect. 4).
Six criteria were considered in making the selection of the study catchments including (i) catchment area (an upper limit of 1000 km2); (ii) streamflow record length (cut off record length was 20 years); (iii) regulation (largely unregulated); (iv) urbanisation (catchments having more than 10% of the area affected by urbanisation were excluded); (v) land use change (catchments known to have undergone major land use changes such as clearing of forest were excluded); and (vi) quality of streamflow data (stations graded as poor quality by the gauging authority were excluded).
The AMF series of the selected catchments were prepared by adopting standard exploratory data analysis procedure which refers to the process of performing the initial investigations on a given dataset so as to maximise insight into a dataset, to check gross data error, to detect outliers and to check underlying assumptions with the help of summary statistics and graphical representations. Most of the detected low outliers occurred for stations which are in low rainfall areas, especially in the western parts of NSW, VIC and QLD. The detected low outliers were treated as censored flows in FFA using FLIKE software (Kuczera and Franks, 2019). The details of the exploratory data analysis for the selected catchments can be found in Rahman et al. (2019).
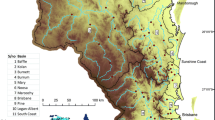
The physiography of the study region is stretching from the lowlands in the western part of VIC to the highlands in the eastern part of VIC and NSW. In the lowlands, the mean catchment elevation is less than 300 m above mean sea level (ASL), while in the high land area, the mean catchment elevation is about 800 ASL. The MAR of the study region ranges from 400 mmyr − 1 (in the north-western part of VIC, which is mainly dominated by winter rainfall) to 4500 mmyr − 1 (in the eastern parts of QLD, which is dominated by summer rainfall). The catchments in the drier parts of these three states, represented as the arid/semi-arid catchments (Rahman et al. 2019)), have not been used in this study. The geographical distribution of the study area is shown in Fig. 1, which shows that most of the selected catchments fall within the proximity of the coastline. These catchments are rural, not affected by major regulation and land use changes and are small to medium in size having catchment areas in the range of 0.6 to 1036 km2. Also, about 77% of the total number of catchments have AMF data lengths larger than 30 years. Detail statistics of the dataset, including streamflow record lengths (range, mean, median), catchment sizes (range, mean, median) and mean annual rainfall (MAR) (range, mean, median) are presented in Table 1.
In previous RFFA studies in Australia (Haddad and Rahman 2012; Aziz et al. 2014), several physiographical and meteorological predictor variables were adopted such as catchment area, design rainfall intensity, MAR, mean annual evapo-transpiration, stream density, mainstream slope and stream length. It should be noted that kriging-based model does not need many catchment characteristics as with many other RFFA techniques (such as Quantile Regression Technique); in this study, catchment area is needed to scale the dependent variable (which is flood quantile here).
2.2 Structure of the analysis
The adopted RFFA approach consists of estimating at-site flood quantiles by fitting a LP3 distribution with the Bayesian parameter estimation procedure (using FLIKE software) at the selected stations and developing ordinary kriging-based RFFA model. The developed RFFA model is tested to each of the selected catchments independently so that the validation statistics can be used as an indication how the kriging-based RFFA model will be performing for the real ungauged catchments of eastern Australia.
2.2.1 At-site flood frequency analysis (FFA)
At-site FFA seeks to relate the magnitude and frequency of flood data, by choosing and fitting a probability distribution model to a dataset at a given site (Stedinger et al., 1993). In this study, an at-site FFA is carried out in order to estimate flood quantiles at each of the selected stations by fitting a log Pearson type 3 (LP3) distribution with the Bayesian parameter estimation procedure using FLIKE software (Kuczera and Franks 2019). LP3 distribution is chosen here since this distribution has shown better FFA results in the past studies for Australian catchments (Haddad et al. 2012; Haddad and Rahman 2012). The LP3 model has the probability distribution function as Eq. 1.
where α, β and γ are shape, scale and location parameters, respectively, with \(\tau \left( \alpha \right)\) being the gamma function. If β > 0, the distribution has a positive skewness and x \(\ge \gamma\). If β < 0, the distribution has a negative skewness and x \(\le \gamma\).
The parameters of the LP3 distribution and the associated moments (i.e. mean, standard deviation and skewness) are extracted from the FLIKE software for use with the RFFA. The software has facilitated (i) using time series data; (ii) safely censoring the data which are too low; (iii) integration of the multiple Grubbs–Beck test for low outlier identification; and (iv) combining regional information (from ‘RFFE Model 2016’) as prior knowledge. The flood quantile estimates from the LP3 distribution are described by Eq. 2.
where \(\overline{{Q_{{\text{T}}} }}\) and S are mean and standard deviation of the base-10 logarithms of AMF data and \(K_{{\text{T}}}\) is a frequency factor that is a function of the skewness coefficient and return period T.
2.2.2 Kriging-based regional flood frequency analysis
Geostatistics-based RFFA is comprised of two major steps in general, which are (i) creating physiographical space and (ii) using interpolation methods within that physiographical space. The physiographical space is defined as a multidimensional space and its coordinate is attained by geomorphological parameters of each catchment using multivariate statistical methods. Hence, catchments with similar climatic and physiographical properties would have the same coordinates along the space. Consequently, each catchment can be placed as one point along the physiographical space and the values for the measured quantity (at-site flood quantiles with different ARIs) are considered as the third axis. Therefore, interpolation method can be incorporated adopting a standard interpolation algorithm, such as kriging methods, where catchments with similar characteristics have similar coordinates in general along the physiographic space (Castiglioni et al. 2009; Durocher et al. 2019). Finally, by using an interpolation method (e.g. kriging), flood quantile estimation is obtained for each of the ARIs individually.
In this study, kriging model was applied to estimate flood quantiles at ungauged catchments. Here, a gauged catchment is assumed to be ungauged, the kriging model is developed without this gauged catchment (referred to as test catchment) and the developed kriging model is used to estimate the flood quantile at the test catchment. While there are many considerations in the development of a kriging model, this analysis mainly considers the spatial correlation between different data points and the distribution of the parameters along the structural function called ‘variogram’ (Persiano et al. 2021). The robustness of kriging heavily depends on proper selection of a variogram model that demonstrates the degree of spatial correlation in the dataset. The variogram model is integrated over the catchment areas associated with each catchment and can be characterised by three parameters: ‘nugget’, ‘sill’ and ‘range’. A ‘nugget’ effect is added to the model to identify the level of uncertainty relating to the sampling or localisation errors, while a ‘sill’ effect is added to represent the regional semivariance, and the ‘range’ represents the distance at which the observed points are spatially correlated and the semivariance is best approximated. These graphical parameters are used together with the distance matrix to estimate the value of the variable of interest at unsampled locations. This integrated variogram depends on the point variogram as well as the sizes, the relative positions and the ‘nestedness’ of catchments. In some previous hydrologic applications of kriging, the semivariance, which is modelled by the semivariogram, has been assumed to be temporally constant; this is clearly not the case for the reconstruction of historical time series of streamflow and flood quantiles.
Let P(u) be a random variable defined at location u and be a second-order stationary random field in a spatial domain. Under the second-order stationarity assumption, the spatial variation structure of P(u) is independent of spatial location and is characterised by a semivariogram model defined as Eq. 3.
The model refers to a linear one due to its weighted linear combination of observed values. Here, the estimated value P for a location u (which refers to the coordinates of the respective catchment outlet) is a weighted linear combination of the values from n reference points. Using the predefined co-variance model, the weights \(\lambda_{i}\) are assigned so that the estimation variance is minimal. The unbiasedness of Eq. 3 is satisfied with unit-sum weights as derived in Eq. 4.
The assumption of the best linear unbiased estimator then gives the kriging weights which are used to estimate the flood quantile for each catchment from the observed flood quantiles of neighbouring stations for the same ARI, weighted by the kriging weights. Thus, a theoretical (predicted) model is fitted to the experimental (observed) variogram. In developing the kriging-based RFFA technique in this study, the estimated flood quantiles are standardised. This standardisation is done as QT/Ab where b is the slope of the linear regression line fitted between ln(A) (as x-axis) and ln(QT) (as y-axis).
In a typical validation approach, a certain portion of the dataset (e.g. 10%) is left out while developing the model, and then, the developed model is verified on the left-out dataset, which is not used in the model development (i.e. validation dataset). The validation procedure helps to select an appropriate model according to its prediction ability, while at the same time evaluating the prediction ability of the model for ungauged catchments.
A jackknifing LOO cross-validation technique is applied in this study to evaluate the relative accuracy of the estimated flood quantiles by the developed kriging-based RFFA model (Haddad and Rahman 2020). In LOO, one gauged catchment is omitted (treated as ungauged) from the database and the flood quantiles for that particular catchment are estimated based on the flood data in other catchments using the kriging method. The process is repeated until all the catchments are independently tested and validated. For example, in this study, all the 558 catchments are considered to have formed one region, then, one catchment is left out for cross-validation and the procedure is repeated for 558 times to implement the LOO validation approach. Hence, the model dataset contains 557 catchments in each iteration step and the model estimation errors are obtained using Eqs. 5 –9.
2.2.3 Model evaluation statistics
A range of evaluation statistics is calculated to evaluate the performance of the kriging-based RFFA model: ratio between predicted and observed flood quantiles (Eq. 5), relative error (RE) (Eq. 6), root mean square normalised error (RMSNE) (Eq. 7), the coefficient of determination (\({R}^{2}\)) (Eq. 8) and absolute relative median error (REm) (Eq. 9).
where \(Q_{{\text{p}}}\) is the flood quantile estimated from the developed kriging-based RFFA model, \(Q_{o}\) is the at-site flood frequency estimate obtained from LP3 distribution using a Bayesian parameter fitting procedure (Kuczera 1999) and \(\overline{Q}_{{\text{o}}}\) is the mean of the observed AMF series at the given site. Here, a \(\frac{{Q_{{\text{p}}} }}{{Q_{{\text{o}}} }}\) ratio closer to 1 indicates a perfect match between the observed and the predicted value, and a smaller median RE is desirable for a model. The performance of the model is also measured in terms of the described \(R^{2}\) in cross-validation, which represents the amount of explained variance by the model and is also affected by both bias and dispersion of the estimators.
It should be noted that the \({Q}_{o}\) are not free from error; these are subject to data error (such as rating curve extrapolation error), sampling error (due to limited record length of AMF series data), error due to the choice of flood frequency distribution and error due to the selection of parameter estimation method. This error undermines the usefulness of the validation statistics (e.g. RE); however, this provides an indication of possible error of the developed RFFA model as far as practical application of the RFFA model is concerned.
3 Results and discussion
3.1 Flood quantile estimation using kriging-based RFFA
Considering that the dataset consists of different types of variables and different scale of values, the data should be rescaled. The procedure considered standardizing the QT values (flood quantiles) of all the sites in the region as if they form a single random sample from a common parent population. The pooled standardised data are fitted to a suitable distribution. For the development of the kriging model, the data series is assumed to be independent. This assumption may be valid if the data being pooled come from stations that are spread over a very large region. To assess the underlying model assumptions, the plots of the standardised residuals vs. predicted values are examined. The predicted values are obtained from the LOO validation. No specific pattern (heteroskedasticity) has been identified, also the standardised values do not exhibit any pattern. Figure 2 shows the spatial plots of the standardised flood quantile for the models Q2, Q5, Q10, Q20, Q50 and Q100; here, Q2 refers 2-year ARI model, Q5 refers 5-year ARI model and so on.
Figure 3 shows the experimental variogram and fitted variogram models with the optimal variogram parameters (e.g. nugget, sill and range) for the six selected flood quantiles (Q2, Q5, Q10, Q20, Q50 and Q100). The figure shows the fitted lines for the developed models being superimposed on the standardised data. Table 2 summarises the results of the kriging analysis, which indicates an increasing trend of ‘sill’ and ‘range’ with the increasing ARIs. The ‘range’ indicates the distance after which the data are no longer significantly correlated, while the ‘sill’ represents the total variance where the empirical variogram appears to be levelled off. Table 2 shows that the ‘nugget’ value is least for Q10 model and it increases with the increasing ARIs from 10 to 100 years; however, the trend differs for Q2 and Q5 models. This indicates that the level of uncertainty increases gradually for the ARIs of 10 to 100 years.
3.2 Performance of the kriging-based RFFA model
The predicted (kriging-based RFFA model) (based on LOO) and observed (at-site FFA model) flood quantiles for the 558 stations are plotted in Fig. 4, which is a measure of how well the flood quantiles could be estimated in ungauged catchments in the study area. Here, the observed flood quantiles are estimated using the LP3 distribution and Bayesian parameter estimation procedure as mentioned before. Figure 4 shows a good agreement overall between the predicted and observed flood quantiles; however, it exhibits a slightly more underestimation as well as a scatter around the 45-degree line (red line). Most of the test catchments are within a narrow range of variability from the 45-degree line except for a few outliers. In broad spectrum, Fig. 4 shows that the predicted and observed flood quantiles show a good agreement for ARIs of 2 to 100 years.
Figure 5 shows the performance of the models for six selected ARIs for each of the three states and when these three states are combined, based on a ratio statistic and RE (%) values. The ratio statistic (Eq. 5) gives an indication of the degree of bias (i.e. systematic, over or under estimation), where a value of 1 indicates good ‘average’ agreement between the Qp and Qo, while RE (Eq. 6) values indicates the prediction bias. In terms of the ratio statistics, the model Q2 for NSW shows noticeable underestimation by the kriging-based RFFA model as the ratio value is located well below the 1–1 line. Here, the best agreement between the Qp and Qo is found for ARIs of 5, 10 and 20 years (see Fig. 5) and a reasonable degree of agreement is found for ARIs of 50 and 100 years. In general, the spread of the ratio values is found very similar for all three states.
Figure 5 shows that the median RE values (represented by the thick black lines within the boxes) are located very close to the zero RE line (indicated by 0 – 0 horizontal line), in particular for ARIs of 5, 10 and 20 years. For Q2 model, the median RE value shows the highest departure (especially for NSW), which indicates an underestimation by the kriging-based RFFA model. But largely, the median RE values match with the zero RE line closely as shown in Fig. 5. In terms of the spread of the RE (represented by the width of the box), Q2 and Q100 models present the highest RE band and Q20 and Q10 models present the smallest RE band, followed by Q5 and Q50 models. This implies that kriging-based RFFA model provides the most accurate flood quantile estimates for Q20 and Q10 models, and the least accurate flood quantiles for Q2 and Q100 models.
Figure 6 shows the cumulative distributions function (CDF) of the Qp/Qo ratio values for all three states and eastern Australia (combined) for 20- and 50-year ARIs. The reason of adopting 20 and 50 years of ARI is that these are the most frequently applied ARI model in hydrologic design. Here, for both Q20 and Q50 models, QLD shows the best result as the median ratio is the closest to the line corresponding to Qp/Qo = 1 (1–1 line) and while, VIC shows the highest degree of bias among the three states. The CDF of the RE values for all three states are also shown in Fig. 6 for 20- and 50-year ARIs; the plot demonstrates the similar result as CDF of ratio statistics that for both Q20 and Q50 models, QLD shows the best results and VIC shows the highest degree of bias.
In this study, an objective assessment of the developed models is also performed by adopting the numerical evaluation statistics given in Eq. (7), Eq. (8) and Eq. (9), in which RMSNE and \({R}^{2}\) are associated with the predictive error variance, while REm is related mostly with the prediction bias. Using the LOO validation, the evaluation statistics are calculated; the results are given in Table 3. Numerical values of these statistics indicate that the models Q20 and Q10 for all the three states (i.e. NSW, VIC and QLD) perform the best among the six quantiles, while the flood quantile estimates obtained for Q2 and Q100 model are found to be more biased (i.e. higher REm) and are of a lesser accuracy (i.e. higher RMSNE). This is observed for all three states; however, the results of VIC show overall poorer performance comparing with the other two states.
Table 3 shows that in the case of Q10, the spatial variance is relatively low; on the other hand, the spatial variance of Q100 is relatively high, indicating that the percentage error is on average high (i.e. lower R2 value) when the flood events get rarer. Here, the RMSNE value shows that, for EA, the least erroneous estimation is achieved for Q5 and Q10 model (RMSNE = 0.16), which is followed by Q20, while the RMSNE value is found to be the highest for 100-year ARI model (RMSNE = 0.24). This also indicates that the model performance decreases with the increasing ARIs from 10 to 100 years. Additionally, Table 3 shows that (i) there is not much difference in accuracy (RMSNE) for NSW and QLD states and also in relation to bias (REm); both the states are found to be very similar for all six ARI models, but overall, QLD shows slightly better accuracy over NSW and a lot better from VIC; (ii) the model Q10 performs best among the six quantiles, which is followed by the models Q5 and Q20; and (iii) largely, the results from the evaluation statistics indicate that the kriging is indeed a viable approach for RFFA in Australia as an alternative to the commonly applied RFFA approaches.
The error statistics of the developed kriging model are comparable to RFFA studies carried out in other countries (e.g. Durocher et al. 2018; Chebana et al. 2014 ; Rahman et al. 2020).
Publications in the international refereed literature on RFFA studies have been scrutinised to compare the performances of the developed kriging-based RFFA model. The advantage of this type of meta-analysis is that a wide range of environments, climates and hydrological processes can be considered in the validation, which goes beyond what can be reasonably achieved by a single study within a country. The study is essentially a comparative assessment that synthesises the results from the available international literature. The results in the literature are reported in an aggregated way in most cases, i.e. as average or median performance over the study region or part of the study region.
Table 4 lists 15 RFFA studies considered in this comparison. It includes summary information about the study region, RFFA method applied and the predictive performance in terms of the root mean square normalised error (RMSNE) as defined in Eq. 7. RMSNE is a common error measure for estimators, combining both the bias and the dispersion component of the error. The target flood quantile, on which this performance is reported, is 100 yr ARI flood quantile, Q100. RMSNE measures are estimated by LOO. The flood regionalisation methods represented in the assessment included: (i) regression methods (R), 5 studies from different regression models where the flood quantiles or the distribution parameters had been transferred to ungauged basins; (ii) index methods (IM), 7 studies where a regional growth curve had been defined for homogeneous regions; and (iii) geostatistical (G) methods, 3 studies where runoff at the target site was estimated as a weighted mean of runoff at the surrounding gauges. While the assessments made by the literature are not based on exactly the same RFFA approach, the methodology is similar. It is interesting to note that the numbers of studies applying regression and index methods are larger than those applying geostatistical methods, which is because they are quite common in hydrology.
Table 4 shows that the geostatistical methods (ordinary kriging model falls in this group) perform the best (RMSNE of 0.30–0.52) across the selected studies, although the number of studies is small compared to other groups. For example, Merz and Blöschl (2005) in Austria and Walther et al. (2011) in Saxony (Germany), provided the combination of the necessary stream network density and non-arid climate leading to lower RMSNE values (0.30 and 0.46, respectively). Table 4 also shows that the geostatistical studies have been applied generally in data-rich environments, which partly explain why they perform better. For instance, the study by Merz and Blöschl (2005) used a large number of catchments (575) and provided the best performance with RMSNE value of 0.30.
Figure 7 shows that the studies listed in Table 4 cover a variety of countries and climate. Figure 7 also shows that the developed ordinary kriging-based RFFA model (which falls under geostatistical method) provides a promising performance in eastern Australia (data-rich regions in Australia having the necessary stream network density) with the least RMSNE value (0.24) followed by Austria (0.30) and China (0.31).
3.3 Comparison of the kriging-based RFFA with ‘RFFE model 2016’
In this section, a detailed comparison is made to evaluate the performance of the kriging-based RFFA technique with the currently recommended RFFA technique in the ARR 2019, known as ‘RFFE Model 2016’. The aim is to generalise the findings of the predictive performance or to understand whether there are general patterns of performance in a given environment for the kriging-based RFFA model and generalised least-squares (GLS)-based quantile regression technique used to develop ‘RFFE Model 2016’.
Figure 8 compares the predicted flood quantiles (estimated by LOO validation) for the selected 558 test catchments in eastern Australia (176 catchments in NSW, 186 catchments in VIC and 196 catchments in QLD), from the kriging-based RFFA model with the predicted flood quantiles from the GLS-based quantile regression technique (RFFE Model 2016) for the 6 selected ARIs (Q2, Q5, Q10, Q20, Q50 and Q100). Both the predicted quantiles are individually compared with the observed flood quantiles, estimated by LP3 distribution and Bayesian parameter estimation procedure (using FLIKE software) as discussed in Sect. 3.1. It should be noted here that the observed flood quantiles are subjected to errors (such as rating curve extrapolation error, sampling error, error due to the choice of flood frequency distribution and error due to selection of parameter estimation method), which provide an indication of possible error of the developed RFFA model as far as the practical application of RFFA model is concerned.
Figure 8 shows the plot of predicted flood quantiles by the kriging-based RFFA model against observed flood quantiles in its left side; the plot of predicted flood quantiles by the ‘RFFE model 2016’and the observed flood quantiles for the corresponding ARIs in its right side individually for each of the three states.
Figure 8 demonstrates that most of the test catchments are within a narrow range of variability from the 45-degree line (red line) except for a few outliers. But, overall a better agreement between the predicted and the observed flood quantiles can be seen for the kriging-based RFFA model as it shows a greater scatter for the ‘RFFE Model 2016’ around the 45-degree line than the ordinary kriging-based RFFA model (see Fig. 8). This is the case for all three states (NSW, VIC and QLD) and the results are very similar in particular for ARIs of 2, 5, 10 and 20 years. The models, Q50 and Q100 (i.e. for the higher discharges), exhibit relatively better results by the kriging-based RFFA technique than the ‘RFFE Model 2016’. For ARI of 2 years, there is a noticeable scatter at smaller discharges for both kriging and ‘RFFE Model 2016’ models.
Figure 9 shows the boxplot of the RE values (Eq. 6) (obtained by LOO validation) of the selected test catchments for the kriging-based RFFA model and ‘RFFE Model 2016’ for different return periods. Figure 9 shows that the median RE values (represented by the black line within the boxes) match with the 0 – 0 line reasonably better for the kriging-based RFFA model as compared to ‘RFFE Model 2016’. For ARIs of 2 years, the median RE value is located notably below the zero line and also the highest departure is noticed, which indicates an underestimation by the kriging-based RFFA model for 2-year ARI.
Conversely, for ‘RFFE Model 2016’, the median RE values for ARIs of 50 and 100 years are located well below the zero line with ARI of 50 years showing the highest departure, while for ARIs of 2 years, the median RE value of is located above the zero line for all three states, which indicates an overestimation by the model. In terms of the RE band (represented by the spread of the box), the kriging-based RFFA model shows smaller box width as compared with the ‘RFFE Model 2016’. This indicates a smaller variability/standard error for all six quantiles for the kriging-based RFFA model. For the kriging-based RFFA model, the smallest spread is found for ARIs of 10 and 20 years, followed by ARIs of 5, 50, 100 and 2 years (see Fig. 9). For all six quantiles, the box widths for the kriging-based RFFA model are about half of those of the ‘RFFE Model 2016’. This is a significant result in favour of the kriging-based RFFA model as far as variability/standard error is concerned; however, there are more outliers (shown by small circles) in the RE plot (as shown in Fig. 9) for the kriging-based RFFA model than the ‘RFFE Model 2016’. This is a concern for the kriging-based RFFA model since this contributes to a higher standard error of flood quantile estimates. These outliers for the kriging-based RFFA model (see Fig. 9) need further investigation for possible data errors. If these catchments are found to be genuine outliers, they should be removed from the dataset to enhance the performance of the kriging-based RFFA model; however, this has not been undertaken in this study.
Figure 9 also presents the boxplot of the Qpred/Qobs ratio values (Eq. 5) of the selected test catchments in eastern Australia (NSW, VIC and QLD) for the kriging-based RFFA model along with the ‘RFFE Model 2016’ for different ARIs. The figure shows that the median Qobs/Qpred ratio values (represented by the thick black lines within the boxes) are located closer to 1 – 1 line (the horizontal line), in particular for ARIs of 5, 10 and 20 years (the best agreement is for ARI of 5 years) for the ordinary kriging-based RFFA model. However, ‘for RFFE Model 2016’, the median Qobs/Qpred ratio value for each quantile locates a short distance above the 1 – 1 line, indicating an overestimation by this model. The model Q2 for RFFE shows a noticeable overestimation by the ‘RFFE Model 2016’. In terms of the spread of the Qobs/Qpred ratio values, for the kriging-based RFFA model, ARIs of 5, 10 and 20 years exhibit the similar (and the lowest) spread followed by ARIs of 50 years. For ‘RFFE Model 2016’ model, the spreads of the Qobs/Qpred ratio values for ARIs of 5 and 10 years also exhibit the lowest level, while ARIs of 50 and 100 years exhibit the largest spread.
Considering, the Qobs/Qpred ratio and the RE values as discussed above, it can be concluded that the kriging-based RFFA model largely provides better flood quantile estimates for medium ARIs (10 to 20 years), i.e. for Q10 and Q20 models.
Finally, considering all the test catchments, Table 5 summarises the results of the median absolute RE values (Eq. 9) for both kriging-based RFFA model and the ‘RFFE Model 2016’. In case of the kriging-based RFFA model, the median RE values range from 38.2% to 35.9% for NSW, 36.2% to 39.1% for VIC and 27.1% to 35.1% for QLD. The smallest and highest median RE values are found for Q10 and Q100 model, respectively, for both NSW and QLD, while in VIC the smallest and highest median RE values are found for ARIs of 5 and 100 years. For the kriging-based RFFA model, the best value is obtained in case of Q10, QLD (27.1%) and the highest median RE (%) value is obtained for Q100 for VIC (39.1%). In comparison with RFFE model, the ordinary kriging model shows much smaller median RE values for all the 6 ARIs for all the three states NSW, VIC and QLD.
3.4 Identification of the best and the worst performing catchments
This section identifies the best (having RE value close to zero line in the boxplot of Fig. 9) and the worst (having RE value furthest from the zero line) performing catchments for the kriging-based RFFA model. Here, the spatial distributions of the relative error (RE) values for the kriging-based RFFA model for all the 176 test catchments of NSW, 186 test catchments of VIC and 196 test catchments of QLD are evaluated and examined more closely.
Figure 10 shows the spatial distribution of RE values across NSW, VIC and QLD considering 20 years of ARI (Q20). The reason of adopting Q20 model is that this is one of the most frequently applied ARI models in hydrologic design. For the validation study, it is important to observe how many test catchments fall within the specified ranges of RE. For this purpose, RE (%) values for the kriging-based RFFA model are grouped into four classes as shown in Table 6. The selected arbitrary ranges of RE (%) are ((\(<\) 25%), marked green in Fig. 10), ((25–50%), marked dark green in Fig. 10), ((50–100%), marked orange in Fig. 10) and ((\(>\) 100%), marked red in Fig. 10).
In the range of RE (\(<\) 25%), the QLD is placed at rank 1 with 46% of the 196 test catchments falling in this range, followed by NSW (42%) and VIC (33%). In case of (25–50%) of RE, a total of 59 (34%) test catchments falls under this category for NSW, which is very closely followed by VIC (33%) and QLD (32%). In the range of both (50–100%) and (\(>\) 100%) of RE, VIC is found to be placed at rank 1 with 22% and 12% of the test catchments falling in this range, respectively. NSW is placed at rank 2, with 14% and 10%, followed by QLD to be ranked at 3 with 12% and 10% of the total test catchments falling in these classifications. Overall, the kriging model performs best for QLD in terms of the distributions of RE (%) values, which is followed by NSW and VIC.
The spatial distribution of RE (%) values across NSW, VIC and QLD shows that most of the selected catchments fall near the coastal area of the region and also in the eastern part of each state (see Fig. 10), since not many catchments met the catchment selection criteria from the western part of the states. Figure 10 also identifies the best performing catchments (having smaller RE values (\(\le 25\%\), marked in green)) along with their respective RE values for the kriging-based RFFA model. For NSW, the catchments near the north-eastern part are found to be exhibiting smaller RE values; for VIC, the catchments close to NSW are found to be exhibiting slightly smaller RE values, while for QLD, the catchments close to NSW and QLD border are found to be exhibiting a slightly better result with respect to RE values. But largely, for all three states, no noticeable spatial trend of the RE values is found across the state.
Figure 11 shows 18 (in NSW) poor performing catchments for the kriging-based RFFA model having higher RE values (\(\ge 100\%\)). Figure 11 also shows the corresponding RE values for ‘RFFE Model 2016’ for comparison. In NSW, 8 catchments (out of 18) have been found to be poorly performing for both the kriging-based RFFA model and ‘RFFE Model 2016’. In VIC, among 23 poor performing catchments for the kriging-based RFFA model, 16 catchments are found to be poor performing in ‘RFFE Model 2016’ as well. Similarly, in QLD, 12 catchments (out of 19) have been found to be poorly performing for both the kriging-based RFFA model and ‘RFFE Model 2016’.
Among 60 poorly performed catchments in the developed model, 36 catchments are found having higher RE for both the kriging-based RFFA model and ‘RFFE Model 2016’. These catchments need further investigation, which, however, is not undertaken in this study. There are few catchments where the developed kriging-based RFFA model shows relatively higher RE than the ‘RFFE Model 2016’, which indicates that there are limitations with both the kriging-based RFFA model and ‘RFFE Model 2016’ and the kriging-based RFFA model can provide poor results in some cases too.
4 Conclusion
Australia is a vast continent with numerous streams, many of which are ungauged or have little or no recorded flood data. RFFA techniques are important for Australia, as they can provide reasonably accurate flood quantile estimation for the numerous ungauged or poorly gauged catchments. There have been many RFFA techniques which have been proposed and used over the years in Australia, but most of them are associated with significant error in flood quantile estimates. To enhance the accuracy of RFFA methods in Australia, there is a need for the further research of new RFFA methods that have not been developed and tested in Australia. This study has undertaken this task. No previous study in Australia focused on kriging-based RFFA model development and testing using a comprehensive flood database. The analysis indicates that the developed kriging-based RFFA model provides a very positive performance in eastern Australia (NSW, VIC and QLD), where stream gauging density is relatively better than other parts of Australia.
Methods used and developed in this study were centred on flood quantile estimation in ungauged catchments in the range of frequent to rare ARIs (2, 5, 10, 20, 50 and 100 years). A total of 586 catchments, located across the three states of eastern Australia (NSW, VIC and QLD), have been selected as the study catchments. The reason for selecting these three states (data-rich regions in the latest version of ARR 2019 (ed. Ball et al., 2019)) is that there are good numbers of high-quality stream gauging stations in these states that can be used in the proposed RFFA study. The results from the validation study (using a LOO) indicate that the kriging-based RFFA model performs best in QLD of the three states in eastern Australia, which is followed by NSW and VIC. The best (having RE value < 25%) and the worst (having RE > 100%) performing catchments in each state (NSW, VIC and QLD) have been identified for the developed kriging-based RFFA model. In general, for all three states, it has found that the kriging-based RFFA model largely provides better flood quantile estimates for medium ARIs (10 to 20 years), i.e. for Q10 and Q20 models. Besides, the developed model is found to outperform the ‘RFFE model 2016’ overall. The spatial distributions of the RE values have shown that there is no noticeable spatial trend across the three states in eastern Australia. Also, it appears that it is difficult to generalise the findings from individual case studies which involve different levels of details on the region of interests.
The kriging-based RFFA models developed in this study were based on the flood database available up to the year 2011 for most of the catchments. It is expected that availability of a more up-to-date comprehensive database (in terms of both quality and quantity) will further improve the predictive performance of the method, which, however, needs to be investigated in future when such a database is available. For at-site FFA, a single standard distribution (LP3 distribution) is adopted, but the 586 catchments may not be fully represented by the selected distribution, and hence, other distributions should be tested. Some outliers can be seen for all six ARIs, which may need to be examined more closely for data errors or issues regarding the hydrology and physical characteristics of these catchments; if these catchments are deemed to be genuine outliers, they should be removed to enhance the performance of the kriging-based RFFA technique; however, this has not been undertaken in this study. All related variables such as seasonal runoff, flow duration curves, low flows and high flows are not included in the study to interpret the differences in performance of the kriging-based RFFA models in terms of the underlying climate and catchment characteristics. Despite these potential limitations, this study emphasises the usefulness of flood quantile estimates in ungauged catchments by exploiting the spatial correlation of flood data or flood statistics over geographical space in RFFA. A detailed comparative approach focused on the understanding of individual variables and how they are connected may provide more insights and eventually lead to better predictions across places (the different catchments/the regions of Australia) and across scales (small and large catchments, see Blöschl et al. 2013) than solely focusing on reproducing the flood quantiles. Some limitations of the adopted method are that this is applicable to the region where streamflow gauging density is relatively higher, and this does not consider catchment characteristics directly in model formulation. The future studies should focus on use of catchment characteristics in kriging, account for scaling effects and impacts of climate change in flood quantile estimation by kriging-based RFFA techniques.
Data availability
The primary data used in this analysis can be obtained from Australian Bureau of Meteorology and other water authorities in Australia by paying a prescribed fee.
Abbreviations
- AMF:
-
Annual maximum flood
- ARI:
-
Average recurrence interval
- ARR :
-
Australian Rainfall and Runoff
- EA:
-
Eastern Australia
- FFA :
-
Flood frequency analysis
- FLIKE:
-
Flood frequency analysis software
- LOO:
-
Leave-one-out validation
- LP3 :
-
Log Pearson type III
- MAR:
-
Mean annual rainfall
- NSW:
-
New South Wales
- PUB:
-
Prediction in Ungauged Basins
- QLD:
-
Queensland
- RE:
-
Relative error
- REm:
-
Absolute relative median error
- RFFA:
-
Regional flood frequency analysis
- RFFE :
-
Regional flood frequency estimation
- RMSNE:
-
Root mean square normalised error
- ROI :
-
Region of influence
- SA:
-
South Australia
- VIC:
-
Victoria
- α :
-
Shape parameter of LP3 distribution
- β :
-
Scale parameter of LP3 distribution
- γ :
-
Location parameter of LP3 distribution
- \(\tau \left(\alpha \right)\) :
-
Gamma function
- \({K}_{T}\) :
-
Frequency factor
- P(u) :
-
Random variable defined at location u
- Q 2, Q 5, Q 10, Q 20, Q 50 and Q 100 :
-
2-yr, 5-yr, 10-yr, 20-yr, 50-yr and 100-yr ARI flood quantile
- \({Q}_{p}\) :
-
Flood quantile estimated from the developed model
- \({Q}_{o}\) :
-
Flood quantile obtained from LP3 distribution
- \({\overline{Q} }_{o}\) :
-
Mean of the observed AMF series
- \({R}^{2}\) :
-
Coefficient of determination
- T :
-
Return period
- G:
-
Geostatistics-based methods
- IM:
-
Index methods
- R :
-
Regression method
References
Adhikary S, Muttil N, Yilmaz A (2016) Ordinary kriging and genetic programming for spatial estimation of rainfall in the Middle Yarra River catchment. Aust Hydrol Res. https://doi.org/10.2166/nh.2016.196
Archfield SA, Pugliese A, Castellarin A, Skøien JO, Kiang JE (2013) Topological and canonical kriging for design flood prediction in ungauged catchments: an improvement over a traditional regional regression approach? Hydrol Earth Syst Sci 17:1575–1588. https://doi.org/10.5194/hess-17-1575-2013
Aziz K, Rahman A, Fang G, Shrestha S (2014) Application of artificial neural networks in regional flood frequency analysis: a case study for Australia. Stoch Env Res Risk Assess 28(3):541–554
Baidya S, Singh A, Panda SN (2020) Flood frequency analysis. Nat Hazards 100:1137–1158. https://doi.org/10.1007/s11069-019-03853-4
Ball J, Babister M, Nathan R, Weeks W, Weinmann E, Retallick M, Testoni I (Eds) (2019) Australian rainfall and runoff: a Guide to flood estimation, commonwealth of Australia.
Blöschl G, Sivapalan M, Savenije H, Wagener T, Viglione A (eds) (2013) Runoff prediction in ungauged basins: synthesis across processes, places and scales. Cambridge University Press
Bobee B, Cavadias G, Ashkar F, Bernier J, Rasmussen P (1993) Towards a systematic approach to comparing distributions used in flood frequency analysis. J Hydrol 142:21–36
Burn DH (1990a) Evaluation of regional flood frequency analysis with a region of influence approach. Water Resour Res 26(10):2257–2265. https://doi.org/10.1029/WR026i010p02257
Burn DH (1990b) An appraisal of the “region of influence” approach to flood frequency analysis. Hydrol Sci J 35(2):49–165
Castiglioni S, Castellarin A, Montanari A (2009) Prediction of Low-Flow Indices in Ungauged Basins Through Physiographical Space-Based Interpolation. J Hydrol 378:272–280
Castiglioni S, Castellarin A, Montanari A, Skøien JO, Laaha G, Blöschl G (2011) Smooth regional estimation of low-flow indices: physiographical space based interpolation and top-kriging. Hydrol Earth Syst Sci 15:715–727. https://doi.org/10.5194/hess-15-715-2011
Cavadias GS (1990) The canonical correlation approach to regional flood estimation. In: regionalization in hydrology (eds. by MA Beran, M Brilly, A Becker, O Bonacci) (Proc. Ljubljana Symp., April 1990):171–178. IAHS Publ.no. 191.
Chebana F, Ouarda TBMJ (2008) Depth and homogeneity in regional flood frequency analysis. Water Resour Res 44:879–887. https://doi.org/10.1029/WR024i006p00879
Chebana F, Charron C, Ouarda TBMJ, Martel B (2014) Regional frequency analysis at ungauged sites with the generalized additive model. J Hydrometeorol 15(6):2418–2428
Chokmani K, Ouarda T (2004) Physiographical space-based kriging for regional flood frequency estimation at ungauged sites. Water Resour Res 40:1–13. https://doi.org/10.1029/2003WR002983
CRED and UNISDR (2015) The human cost of weather related disasters 1995–2015, UN office for disaster risk reduction (UNISDR) and centre for research on the epidemiology of disasters (CRED). http://www.unisdr.org/files/46796_cop21weatherdisastersreport2015.pdf.
Cunnane C (1988) Methods and merits of regional flood frequency analysis. J Hydrol 100:269–290
Cunnane C (1989) Statistical distributions for flood frequency analysis. world meteorological organisation. operational hydrology report 33
Douglas BC (1995) U.S. National Report to IUGG, 1991–1994. Reviews of Geophysics, 33 Supplement. Online; available at http://www.agu.org/revgeophys/dougla01/dougla01
Durocher M, Burn DH, Zadeh SM (2018) A nationwide regional flood frequency analysis at ungauged sites using ROI/GLS with copulas and super regions. J Hydrol 567:191–202
Durocher M, Burn DH, Mostofi Zadeh S, Ashkar F (2019) Estimating flood quantiles at ungauged sites using nonparametric regression methods with spatial components. Hydrol Sci J 64(9):1056–1070
Engeland K, Hisdal H (2009) A Comparison of Low Flow Estimates in Ungauged Catchments Using Regional Regression and the HBV-Model. Water Resour Manage 23:2567–2586. https://doi.org/10.1007/s11269-008-9397-7
Farmer W (2016) Ordinary kriging as a tool to estimate historical daily streamflow records. Hydrol Earth Syst Sci 20:2721–2735. https://doi.org/10.5194/hess-20-2721-2016
Goovaerts P (2000) Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J Hydrol 228(1–2):113–129
Griffis VW, Stedinger JR (2007) Log-Pearson Type 3 distribution and its application in Flood Frequency Analysis. 1: Distribution characteristics. J Hydrol Eng 12:482–491. https://doi.org/10.1061/(ASCE)1084-0699(2007)12:5(482)
Haddad K, Rahman A (2012) Regional flood frequency analysis in eastern Australia: Bayesian GLS regression-based methods within fixed region and ROI framework – quantile regression vs. parameter regression technique. J Hydrol 430–431(2012):142–161
Haddad K, Rahman A (2019) Development of a large flood regionalisation model considering spatial dependence - application to ungauged catchments in Australia. Water 11:677. https://doi.org/10.3390/w11040677
Haddad K, Rahman A (2020) Regional flood frequency analysis: Evaluation of regions in cluster space using support vector regression. Nat Hazards 102:489–517
Haddad K, Stedinger RA, JR, (2012) Regional flood frequency analysis using bayesian generalized least squares: a comparison between quantile and parameter regression techniques. Hydrol Process 26:1008–1021
Haddad K, Rahman A, Zaman M, Shrestha S (2013) Applicability of Monte Carlo cross validation technique for model development and validation using generalised least squares regression. J Hydrol 482:119–128
Ishak E, Rahman A (2019) Examination of changes in flood data in Australia. Water 11(8):1734. https://doi.org/10.3390/w11081734
Javelle P, Ouarda TBMJ, Lang M, Bob´ee B, Gal´ea G, Gr´esillon JM, (2002) Development of regional flood-durationfrequency curves based on the index-flood method. J Hydrol 258:249–259
Jimenez A, Garcia C, Mediero L, Incio L, Garrote J (2012) Map of maximum flows of intercommunity basins. Revista De Obras Publicas 3533:7–32
Jingyi Z, Hall MJ (2004) Regional flood frequency analysis for the Gan-Ming River basin in China. J Hydrol 296:98–117. https://doi.org/10.1016/j.jhydrol.2004.03.018
Kirby W, Moss M (1987) Summary of flood frequency analysis in the United States. J Hydrol 96:5–14
Kjeldsen TR, Jones DA (2010) Predicting the index flood in ungauged UK catchments: on the link between data-transfer and spatial model error structure. J Hydrol 387:1–9
Kuczera G (1999) Comprehensive at-site flood frequency analysis using Monte Carlo Bayesian inference. Water Resour Res 35(5):551–1557
Kuczera G, Franks S (2019) At-site flood frequency analysis. In: Australian rainfall & runoff, Chapter 2, Book 3, edited by Ball et al., Commonwealth of Australia
Laaha G, Skøien JO, Bloschl G (2012). Spatial prediction on river networks comparison of top-kriging with regional regression Hydrological Processes. https://doi.org/10.1002/hyp.9578
Leclerc M, Ouarda TBMJ (2007) Non-stationary regional flood frequency analysis at ungauged sites. J Hydrol 343:254–265. https://doi.org/10.1016/j.jhydrol.2007.06.021
Madsen H, Rasmussen PF, Rosbjerg D (1997) Comparison of annual maximum series and partial duration series methods for modeling extreme hydrologic events: 1. At-Site Modeling Water Resour Res 33:747. https://doi.org/10.1029/96WR03848
Meigh J, Farquharson F, Sutcliffe J (1997) A worldwide comparison of regional flood estimation methods and climate. Hydrol Sci J 42:225–244
Merz R, Blöschl G (2005) Flood frequency regionalisation-spatial proximity vs. catchment attributes. J Hydrol 302:283–306. https://doi.org/10.1016/j.jhydrol.2004.07.018
Meral A, Eroğlu E (2021) Evaluation of flood risk analyses with AHP, Kriging, and weighted sum models: example of Çapakçur, Yeşilköy, and Yamaç microcatchments. Environ Monit Assess 193(8):1–15
Merz R, Blöschl G, Humer G (2008) National flood discharge mapping in Austria. Nat Hazards 46(1):53–72
Merz Bl¨oschl RG (2005) Flood frequency regionalisation-spatial proximity vs. catchment attributes. J Hydrol 302:283–306. https://doi.org/10.1016/j.jhydrol.2004.07.018
Micevski T, Hackelbusch A, Haddad K, Kuczera G, Rahman A (2015) Regionalisation of the parameters of the log-Pearson 3 distribution: a case study for New South Wales. Aust Hydrol Process 29(2):250–260
National Research Council (1988) estimating probabilities of extreme floods: methods and recommended research, 141, National Academy Press, Washington D.C.
OECD (2016) Financial management of flood risk. OECD Publishing, Paris. https://doi.org/10.1787/9789264257689-en
Ouarda TBMJ, Girard C, Cavadias GS, Bobée B (2001) Regional flood frequency estimation with canonical correlation analysis. J Hydrol 254:157–173
Ouarda TBMJ, Ba KM, Diaz-Delgado C, Carsteanu A, Chokmani K, Gingras H, Quentin E, Trujillo E, Bob´ee B, (2008) Intercomparison of regional flood frequency estimation methods at ungauged sites for a Mexican case study. J Hydrol 348:40–58. https://doi.org/10.1016/j.jhydrol.2007.09.031
Ouarda T, Charron C, St-Hilaire A (2008) Statistical models and the estimation of low flows. Canadian Water Resour J 33:195–206. https://doi.org/10.4296/cwrj3302195
Pandey GR, Nguyen VTV (1999) A comparative study of regression based methods in regional flood frequency analysis. J Hydrol 225:92–101. https://doi.org/10.1016/S0022-1694(99)00135-3
Parajka J, Viglione A, Rogger M, Salinas JL, Sivapalan M, Bl¨oschl G (2013) Comparative assessment of predictions in ungauged basins – Part 1: Runoff-hydrograph studies. Hydrol Earth Syst Sci 17:1783–1795. https://doi.org/10.5194/hess-17-1783-2013
Persiano S, Salinas JL, Stedinger JR, Farmer WH, Lun D, Viglione A, Castellarin A (2021) A comparison between generalized least squares regression and top-kriging for homogeneous cross-correlated flood regions. Hydrol Sci J 66(4):565–579
Potter KW (1987) Research on flood frequency analysis: 1983–1986. Rev Geophys 25(2):113–118
Potter KW, Lettenmaier DP (1990) A comparison of regional flood frequency estimation mean using a resampling method. Water Resour Res 26(3):424
Ouarda TBMJ, Bâ KM, Diaz-Delgado KM, Cârsteanu CA, Chokmani K, Gingras H, Quentin E, Trujillo E, Bobée B (2008a). Intercomparison of regional flood frequency estimation methods at ungauged sites for a Mexican case study. J Hydrol 348:40–58. https://doi.org/10.1016/j.jhydrol.2007.09.031
Ouarda T, Charron C, St-Hilaire A (2008b) Statistical Models and the Estimation of Low Flows. Canadian Water Res J 33:195206. https://doi.org/10.4296/cwrj3302195.
Rahman A, Charron C, Ouarda T, Chebana F (2018) Development of regional flood frequency analysis techniques using generalized additive models for Australia. Stoch Env Res Risk Assess. https://doi.org/10.1007/s00477-017-1384-1
Rahman A, Haddad K, Kuczera G, Weinmann PE (2019) Regional flood methods. In: Australian rainfall & runoff, Chapter 3, Book 3, edited by Ball et al., Commonwealth of Australia
Rahman AS, Khan Z, Rahman A (2020) Application of independent component analysis in regional flood frequency analysis: comparison between quantile regression and parameter regression techniques. J Hydrol 124372
Salinas JL, Laaha G, Rogger M, Parajka J, Viglione A, Sivapalan M, Bl¨oschl G, (2013) Comparative assessment of predictions in ungauged basins – Part 2: Flood and low flow studies. Hydrological Earth System Sciences 10:411–447. https://doi.org/10.5194/hessd-10-411-2013
Sauquet E (2006) Mapping mean annual river discharges: Geostatistical developments for incorporating river network dependencies. J Hydrol 331:300–314. https://doi.org/10.1016/j.jhydrol.2006.05.018
Sivapalan M, Takeuchi K, Franks SW, Gupta VK, Karambiri H, Lakshmi V, Liang X, McDonnell JJ, Mendiondo EM, O’Connell PE, Oki T, Pomeroy JW, Schertzer D, Uhlenbrook S, Zehe E (2003) IAHS Decade on Predictions in Ungauged Basins (PUB), 2003–2012: Shaping an exciting future for the hydrological sciences. Hydrol Sci J 48:857–880. https://doi.org/10.1623/hysj.48.6.857.51421
Skøien JO, Blöschl G (2007) Spatiotemporal topological kriging of runoff time series. Water Resour Res 43:1–21. https://doi.org/10.1029/2006WR005760
Skøien JO, Merz R, Blöschl G (2006) Top-kriging – geostatistics on stream networks. Hydrological Earth System Sciences 10:277–287. https://doi.org/10.5194/hess-10-277-2006
Stedinger JR, Vogel RM, Foufoula-Georgiou E (1993) Frequency analysis of extreme events, in Handbook of Hydrology, McGraw Hill Book Co., NY, 18.1–18.66 (Chapter 18)
Tran VN, Kim J (2022) Robust and efficient uncertainty quantification for extreme events that deviate significantly from the training dataset using polynomial chaos-kriging. J Hydrol 609:127716
Valizadeh N, Mirzaei M, Allawi MF (2017) Artificial intelligence and geo-statistical models for stream-flow forecasting in ungauged stations: state of the art. Nat Hazards 86:1377–1392. https://doi.org/10.1007/s11069-017-2740-7
Viglione A, Parajka J, Rogger M, Salinas JL, Laaha G, Sivapalan M, Blöschl G (2013) Comparative assessment of predictions in ungauged basins – Part 3: Runoff signatures in Austria. Hydrol Earth System Sci 17:2263–2279. https://doi.org/10.5194/hess-17-2263-2013,2013
Walther J, Merz R, Laaha G, B¨uttner U (2011) Regionalising floods in Saxonia Regionalisierung von Hochwasserabfl¨ussen in Sachsen, in: Hydrologie & Wasserwirtschaft – von der Theorie zur Praxis, edited by: Bl¨oschl, G. und Merz, R., Forum f¨ur Hydrologie und Wasserbewirtschaftung. Heft 30.11:29–35. ISBN:978–3–941897–7 (in German)
Zaman M, Rahman A, Haddad K (2012) Regional flood frequency analysis in arid regions: a case study for Australia. J Hydrol 475:74–83
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions. No funding was received for this research.
Author information
Authors and Affiliations
Contributions
SA conceptualised the problem, collated data, carried out analyses and drafted the manuscript, and A Rahman checked the results and revised the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
Authors declare that there is no conflict of interest and no funding was received for this study. All the authors have read the manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ali, S., Rahman, A. Development of a kriging-based regional flood frequency analysis technique for South-East Australia. Nat Hazards 114, 2739–2765 (2022). https://doi.org/10.1007/s11069-022-05488-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-022-05488-4