1 Introduction

The world is suffering from climate change, and the impact of extreme rainfall events is most obvious in Taiwan. The World Bank’s annual report points out that 73% of Taiwan’s residents and land areas suffer from three or more types of natural disasters. Compared with other countries in the world, Taiwan is regarded as a high disaster risk area (Xu et al. 2011). Mountain roads are important infrastructure for sloping communities and important protection targets for disaster prevention in watersheds. The frequency and intensity of heavy rainfall may continue to increase, and the impact of rainfall on-road sediment disasters in mountainous areas can easily lead to the formation of isolated communities. As the frequency and intensity of disasters increase, maintaining road safety becomes more and more difficult. If the disaster hot spots along the route can be identified before the disaster occurs, appropriate management measures can be taken in advance to reduce losses. In order to achieve the purpose of disaster prevention and mitigation, it has become a trend to study potential sediment disasters on-road slopes.

Previous studies on potential sediment hazards of road slopes can usually be divided into qualitative and quantitative methods (Guzzetti et al. 1999). Qualitative methods are evaluated in the absence of historical event data, mainly based on the experience, judgment, and opinions of experts, such as terrain analysis and expert scoring methods; while quantitative methods have sufficient data in historical event collection and a slope stability evaluation model is established. The slope stability analysis methods can be summarized as: fuzzy method (Leonardi et al. 2020), vulnerability analysis (Zhang et al. 2020), logistic regression (Das et al. 2012; Shao et al. 2020; Sun et al. 2020; Khalaj et al. 2020), finite element method (Pradhan and Siddique 2020), risk analysis (Lin et al. 2017, 2020), linear discriminant analysis (Nepal et al. 2019), regression analysis (Varol et al. 2019), differential InSAR (Nappo et al. 2019), artificial neural networks (Choobbasti et al. 2009; Tsangaratos and Benardos 2013; Varol et al. 2021), and adaptive network-based fuzzy inference system methods (Varol et al. 2021).

Recently risk analysis has been frequently applied in the fields of economy, health, insurance, and disaster prediction (Blanciforti and Luster 2006; Tsai and Chen 2010; Hsu et al. 2011; Marhavilas et al. 2011; Zahran et al. 2011; Braman et al. 2013; Dong et al. 2015). According to the report of the Office of the United Nations Disaster Relief Coordinator, risk is the potential loss of life and property and/or economic activity at a specific natural disaster, and it generally consists of two components, namely, hazard and vulnerability (UNDP 2004; Rausand 2013; Chen and Wu 2016). Risk analysis refers to a combination of opportunities for disaster events and their consequences or losses, where indices have many different combinations and calculations (Cao et al. 2010). Crichton (1999) proposed that risk is the probability of loss, which is determined by the three elements of hazard, vulnerability, and exposure. Based on this risk concept, Lin et al. (2017) proposed a model for handling primary disasters. Since debris from primary disasters may accumulate upstream to form landslide dams, unstable debris dams are easily broken, and the resulting debris flow will have a considerable impact on downstream areas. As a result, Lin et al. (2020) have established another risk model to assess the impact of potential derived disasters on downstream areas.

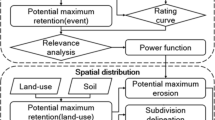
The resilience system is developed from ecology (Holling 1973). Under the current trend of extreme weather, only considering risk analysis is not enough to protect critical infrastructure systems. Combining risk analysis with resilience analysis can provide better disaster management and emergency planning (Park et al. 2013). In the face of short duration and heavy rainfall, the current engineering design standards are almost impossible to resist; in addition, the over-designed objects can cause disasters to expand or shift when the flood overflows and breaks the embankment (Odum et al. 1995). Therefore, under the concept of resilience, an affordable, sustainable, and reasonable optimal management strategy has been developed to deal with natural system disturbances (Bostick et al. 2017). In today’s cities, the issue of flood management is to strengthen the resilience of urban settlements in the face of floods; so that they can quickly resume normal operations after a force majeure natural disaster strikes. Resilience-related enhancements include four main aspects: social resilience, infrastructure resilience, organizational resilience, and economic resilience (Water Resources Agency 2019). In the planning and design of roads and bridges, the concept of "sponge" was used extensively to change the original paving material (Cetin 2013) to make it have the functions of water permeability, water conduction, water storage, cooling, air pollution reduction, and ecological sustainability, and have the ability to resist the impact of disasters and recover after disasters. As roads span different watershed subdivisions, road extension lines are distributed in environmental vulnerabilities with different geographical and hydrological conditions. Since the spatial distribution of event hazards is different, it is appropriate to use environmental indicators to assess potential sediment hazards on roads through risk analysis. Risk-based models can combine conceptual ideals with environmental indicators to assess watershed disasters, which have become a trend due to multi-scale considerations. Grid analysis alone cannot effectively consider the impact of slope disasters on roads. Therefore, this study uses environmental indicators and conceptual models to describe the potential derived disasters in the watershed and explores the possibility of sediment disasters on various sections of roads based on the topographic divisions. In addition to the quantitative analysis of the possibility of sediment disasters along the route, the feasibility of value-added applications in resilience management is also the focus of this research.

2 Materials and methods

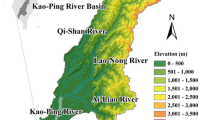
The Chenyulan Creek watershed is located in Nantou County, an area of 448 square kilometers, covering Xinyi, Lugu, and Shuili Townships. The Creek originates from the east of Yushan North Peak and has a total length of 42 km. The watershed is long and narrow, with the mainstream extending from south to north into the Zhoushui River. Seventy percent of the watershed is forest, and the population is concentrated at the banks of streams and at the confluence of the Zhoushui River (Fig. 1a). The important extension roads around the study area are Tai-18, Tai-21, and Tai-16, of which Tai-21 is the main research road. From Shenlong Bridge (the intersection of Zhoushui River and Chenyulan Creek) to Tataga, the road research section of the Chenyulan Creek watershed ranges from 79 to 145 K. According to the disaster data from the Directorate General of Highways of the Ministry of Communications, as shown in Table 1, the typhoon events that have caused damage to Tai-21 over the years are mainly distributed on the mileage mark above 90 K (Fig. 1b).

Fig. 1
figure 1

Basic information of the study area and historical disasters along Tai-21 highway

Full size image
Table 1 Historical sediment disaster on Tai-21 highway
Full size table

2.1 Materials

Terrain analysis and zoning are carried out through the 20 m × 20 m digital elevation model (DEM) resolution provided by the Ministry of Land Administration. The landslide caused by Typhoon Morakot was extracted from the Landsat images of the U.S. Geological Survey as model validation. The spatial distribution of maximum daily rainfall and return period during Typhoon Morakot is calculated using annual and/or daily rainfall data from the Water Resources Agency stations around the Chenyulan Creek watershed. The road attributes data provided by the Taiwan Transport Research Institute, combined with the terrain subdivisions, are used to calculate the distribution of road density and spatial dispersion index in the watershed. The river network extracted from the DEM calculates the river curvature as concave index and analyzes the river order to extract the headward erosion index. The dip-slope map provided by the Central Geological Survey is combined with the topographic wetness index to extract the potential failure scale of the dip slope. Big data provided by governments or agencies (Table 2) were used in this study to establish risk-based models for assessing watershed sediment disasters.

Table 2 Research materials
Full size table

2.2 Methods

2.2.1 Extraction of newly formed bare lands

Image differencing method proposed by Lin et al. (2006) was used to calculate the normalize difference vegetation index (NDVI) change caused by the event to derive the spatial distribution of the newly formed bare land. The result of the extraction was verified using accuracy assessment. The number of samples is calculated according to the formula as follows (Yamane 1967): \(n=\frac{N}{1+N({e}^{2})}\) Where: n is training samples sizes, N is the number of population, and e is the confidence level. Accuracy evaluation is typically calculated using an error matrix that includes overall accuracy, producer’s accuracy, user’s accuracy (Story and Congalton 1986), and Kappa value (Cohen 1960). Because determining the overall accuracy involves weights of each type, and the Kappa value takes into account the relationship between commission error and omission error, the classification results were evaluated herein using overall accuracy assessments and the Kappa value.

2.2.2 Delimitation of watershed subdivisions

The grid unit is mainly used for environmental index analysis and then uses terrain subdivision as boundary running grid statistics for model verification and road segment management reference. The terrain subdivision is based on the automatic division theory of the watershed proposed by Lin et al. (2008). The terrain analysis is carried out using digital elevation model, and the river network is extracted by threshold method.

2.2.3 Collapse ratio and disaster ratio

The collapse data and subdivisions can be used to calculate the collapse ratio and disaster ratio. Collapse ratio refers to the number of subdivisions with collapse out of the total subdivisions for a given risk grade. Subdivision disaster ratio is the ratio of collapse and/or sedimentary area to subdivision area. The former uses subdivision collapse data, only explores whether the collapse occurred, more in line with the concept of collapse risk model, so it can be used to verify the primary disasters of watershed landslides. The latter uses data from collapse and sedimentary zones to calculate the proportion of derived disasters in the subdivision and is used to verify the derived disasters of watershed landslides.

2.2.4 Sediment disaster risk model

Judging by the time of occurrence of disasters, disasters can be further divided into primary and derived disasters. The primary disasters are the initial disasters, and other disasters directly caused by primary disasters may be referred to as derived disasters (Wu et al. 2007). This study uses the concept of risk analysis to evaluate the risk of sediment disaster with different factors and to categorize sediment disasters into primary and derived disasters. The applicable risk model of both is constructed, and the newly formed landslide is extracted by satellite images for model verification.

Primary disaster risk assessment is based on the risk model proposed by Lin et al. (2017). Road development index is calculated from the multiplication of normalized road density and spatial dispersion index, where the SDI proposed by Tsai and Weng (2006) can be expressed as follows:

$$SDI=\frac{1}{\sqrt{A}}\frac{1}{2(n-1)}\sum_{i-1}^{n}\sum_{j-1}^{n}({a}_{i}\%+{a}_{j}\%){\overline{d}}_{(i,j)}$$
(1)

SDI is based on the statistical index of deviation from the mean; \({\overline{d}}_{(i,j)}\) is the dispersion degree of two measured objects, \(({a}_{i}\%+{a}_{j}\%)\) is the weight of \({\overline{d}}_{(i,j)}\), ΣΣ and i ≠ j is the calculated degree of dispersion for one object to the other objects, \(\frac{1}{2(\mathrm{n}-1)}\) is the number of repeated calculation and \(\frac{1}{\sqrt{\mathrm{A}}}\) is a correction for size of statistic unit. The more the objects concentrated, the smaller the SDI derived. In addition to proposing a model for the analysis of the risk of watershed landslides, Lin et al. (2017) also discussed the scale of the landslide based on the overlay calculation of the river concave index, head erosion index, and dip slope index. Potential large-scale collapse locations are usually rich in debris material and have deep soil layers. As a result, areas lacking vegetation coverage are vulnerable to erosion and/or have recently collapsed, making large-scale collapses less likely. Therefore, NDVI was used to appropriately modify the scale of primary disaster.

This study uses three parameters: risk, vulnerability, and exposure to quantify the risk of derived disasters. The external forces of the derived disaster that affect the protected object mainly come from the collapse debris of the primary disaster, so the hazard of derived disaster (Hd) is related to the risk of primary disaster (Rp) and scale of primary disaster (Sp). If the primary disaster occurs in the location of the higher topographic wetness index (TWI), its collapse volume will be larger. In addition, the slope of higher TWI is easy to accumulate unstable debris coupled with its relatively larger watershed area; the accumulation of unstable debris is prone to secondary disasters due to the next torrential event. Hence, TWI can express the vulnerability of the derived disaster. The difficulty of moving the collapse sediment to the protected object also affects the potential of the derived disaster, so the use of sediment delivery ratio (SDR) as the exposure degree (Ed) indicates the degree of exposure of the protected object to the sediment disaster. The calculation of SDR in this study mainly uses the theory put forward by Lin et al. (2002). The SDR for a given cell i can be calculated from the receiving drainage length (LRi) ratio to total drainage length (Li):

$${SDR}_{i}=\frac{{LR}_{i}}{{L}_{i}}$$
(2)

The closer the network of rivers, the more unstable debris is easily eroded into ditches and/or creeks, increasing the likelihood of disasters at protected targets downstream. Finally, the risk of landslide-derived disasters (Rd) can be derived from the multiplication of hazard, vulnerability, and exposure as follows:

$$R_{d} = H_{d} \times V_{d} \times E_{d} = (R_{p} \times S_{p} ) \times TWI \times SDR$$

2.2.5 Resilience management

Holling(1973) proposed an explanation of engineering and ecological resilience. In 2007, Brand and Jax (2007) further put forward the concept of social and ecological resilience covering society, paying more attention to the relationship between social disturbance and reorganization, and exploring organizational transformation, learning, and innovation capabilities. This development shifts the concept of resilience to a higher level of organizational and governance architecture. Depending on the scale of the event, unexpected events in different ecosystems can be further divided into large, medium, and small scales, and conform to the above three different concepts of resilience. The disturbances caused by events of different sizes needed to be addressed by resilience concepts, and that environmental resilience along roads could be assessed through vulnerability and/or exposure indicators.

2.2.6 Landslide-prone slope correction

Lin et al. (2017) proposed a potential watershed landslide model that uses slope factor to correct vulnerability. However, it is incorrect to say that the steeper the slope, the more prone it is to collapse. Therefore, in calculating the collapse slope of the Morakot typhoon event, it is found that its collapse slope is mainly distributed in the middle of the slope distribution, and the distribution is slightly normal. Thus, the normal distribution of the probability density function (PDF) is used as a slope curve prone to landslides to correct vulnerability. The formula for the PDF is as follows:

$$PDF=f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{\frac{{(x-\mu )}^{2}}{2{\sigma }^{2}}}$$
(4)

3 Results

3.1 Primary disaster

Primary disaster risk (RP) is the multiplication of primary disaster (HP) and primary disaster vulnerability (VP), where hazard refers to environmental external forces, and vulnerability refers to the sensitivity of the environment to disasters. The normalized maximum daily rainfall of Typhoon Morakot is calculated as hazard factor (Fig. 2). Road development index is calculated from the multiplication of normalized road density and SDI (Fig. 3). Vulnerability is the overlay calculation of the extreme rainfall index, the green deterioration index, and the road development index, and is then modified by multiplying landslide-prone slope index (Fig. 4). The spatial distribution of the relevant indexes used in the model and the result of primary disaster risk are shown in Fig. 5.

Fig. 2
figure 2

Normalized maximum daily rainfall caused by Typhoon Morakot as hazard factor (Hp)

Full size image
Fig. 3
figure 3

Road development index based on multiplication of road density and SDI

Full size image
Fig. 4
figure 4

Vulnerability (Vp) based on relevant indices

Full size image
Fig. 5
figure 5

Primary disaster risk calculated based on multiplication hazard and vulnerability

Full size image

3.2 Scale of primary disaster

Based on the river concavity index, head erosion index, and dip slope index, the landslide scale of the watershed can be calculated by overlaying the maps (Figs. 6, 7 and 8). The spatial distribution of the relevant indexes used in the model and the result of scale of primary disaster are shown in Fig. 8.

Fig. 6
figure 6

River concave index (left) and head erosion index (right)

Full size image
Fig. 7
figure 7

Dip slope index derived based on dip-slope position and TWI multiplication

Full size image
Fig. 8
figure 8

Primary disaster scale based on relevant indices

Full size image

3.3 Derived disaster

The hazard of derived disaster (Hd) is related to the risk of primary disaster (Rp) and scale of primary disaster (Sp), and the risk of landslide-derived disasters (Rd) can be derived from the multiplication of hazard, vulnerability, and exposure (Fig. 9).

Fig. 9
figure 9

Risk of landslide-derived disasters based on relevant indices

Full size image

3.4 Newly formed bare land extraction

The image differencing method is used to calculate the difference between the satellite image NDVI before the event and the satellite image NDVI after the event. The greater the difference, the more serious the vegetation damage. Compared with aerial photos, the threshold of change is adjusted to extract newly formed bare land (Fig. 10). The landslide extraction process is to check the training sample error through aerial photos. Since the total number of grids in the study area exceeds 100,000, the 95% confidence level is used to calculate the minimum training sample to be 400 grids. Therefore, 200 new and non-new bare lands are randomly selected for classification accuracy analysis. Based on the error matrix analysis, the overall accuracy and Kappa consistency coefficient are calculated. The results show that the overall accuracy is 88.75% and the Kappa coefficient is 0.775 (Table 3).

Fig. 10
figure 10

a Pre-event image b Post-event image c Newly formed bare land d Aerial photo

Full size image
Table 3 Results of error matrix
Full size table

3.5 Division of watershed analysis units

Using the concept of uniform terrain (threshold value: 20 hectares), the watershed can be further divided into 2780 terrain subdivisions according to the river network (Fig. 11). This study uses the combination of subdivision and newly formed landslide to calculate the collapse information of each partition to verify the risk model of sediment disaster in the watershed. Because the spatial resolution of various types of digital terrain models allows semi-grid error, smaller terrain segmentation is easily affected by boundary interference and is error-prone. The disturbance area is mainly distributed in places with high water density and high surface cutting severity. To avoid noise caused by small segmentation, we use correction factors (the area ratio of terrain subdivision to the threshold) to correct interference with the partition boundaries.

Fig. 11
figure 11

Spatial distribution of terrain subdivisions

Full size image

4 Discussions

4.1 Newly formed landslide extraction

The image differencing method is used to calculate the difference between the satellite image NDVI before the event and the satellite image NDVI after the event. The greater the difference, the more serious the vegetation damage. Compared with aerial photos, the threshold of change is adjusted to extract newly formed bare land. Landis and Koch (1977) noted that the Kappa value of greater than 0.75 showed that the classification result is very consistent, indicating that the newly formed bare land extraction is good and can be used to validate the derived disaster risk model and locate the disaster areas caused by the derived disaster (Fig. 10). Since the newly formed bare land extracted from satellite images includes the collapse area and the deposition area caused by the landslide, the deposition area needs to be removed to reflect the true landslide location. When extracting the location of the collapse in a large area, the vegetation degradation area with a slope of less than 6° can be regarded as the deposition location of sediments (Handbook of Soil and Water Conservation 2017). The newly formed bare land (Fig. 10c) minus the new deposition area can get the newly formed landslide (Fig. 12), which can be used to calculate the collapse ratio and disaster ratio of each terrain subdivision for model verification.

Fig. 12
figure 12

The extraction process of collapse and deposition area

Full size image

4.2 Terrain subdivision

Jenson and Domingue (1988) delineated the sub-watersheds using theory of cumulative flow difference, once the cumulative flow difference of the grid is greater than or equal to a given threshold, the grid is the outlet of the sub-watershed, and the upstream catchment area is delineated. According to the concept of terrain homogeneity, the river network was used to further divide the sub-watersheds into left, right, and source subdivisions. Based on the Handbook of Soil and Water Conservation (2017), a gully is defined as a watershed area of less than 20 hectares, beyond which it can be considered a creek. Thus, in this study, the watershed area of the gully was used as a slope unit and 20 hectares were used as a threshold for drawing terrain partitions.

This study uses the combination of subdivisions and newly formed landslides to calculate the collapse information of each partition and verify the watershed sediment disaster risk model. Since the spatial resolution of various digital terrain models allows half-grid error, smaller terrain segmentation is susceptible to boundary interference and error-prone. The disturbance area is mainly distributed in places with high water density and high surface cutting severity. In order to avoid the noise caused by small segmentation, this study introduces a correction factor (the area ratio of terrain subdivision and threshold) to correct the interference to the boundary of the partition.

4.3 Risk and/or scale of primary disaster

In the field of sediment-related primary disasters, few scholars have conducted in-depth studies on the relationship between the probability and scale of watershed collapse. The sediment disasters caused by the collapse of a watershed can be considered as point-source pollution. The unstable slope damage is like energy release, and the probability of its next occurrence is inversely proportional to the scale of the debris release. The relationship between the collapse ratio and risk level of the primary disaster in each subdivision is discussed. The collapse ratio was positively correlated with the risk level, with a determination coefficient of 0.9289 and a significant level of 0.1% (Fig. 13). Interpretation rate of the primary disaster risk model is 92.89%. Figure 14 shows that there is a significant inverse correlation between the landslide scale index and the collapse ratio (R2 = 0.7714). Generally, the areas vulnerable to large-scale landslides generally have unique characteristics in topography, geology, and vegetation, so the comprehensive indicator that integrates indices of river concave, head erosion, and dip slope can effectively reflect the hot spots of potential large-scale landslide and help to understand the relationship between probability and scale of landslides in the watershed.

Fig. 13
figure 13

Relationship between primary disaster risk and collapse ratio

Full size image
Fig. 14
figure 14

Relationship between of landslide scale index and subdivision collapse ratio

Full size image

4.4 Derived disaster

The possible effects of collapsed debris on downstream protective objects are discussed from the point-source transmission perspective. The study found that the high risk of derived disasters is located at the riparian of the creek, which is prone to downstream movement of landslides. Because the hazard of the model is combined with the probability and scale of the primary disaster, the probability and scale of primary disasters show a trade-off (Fig. 14). The maximum hazard calculated according to the model automatically balances the probability and scale of the primary disaster, so the main factors affecting the landslide disaster in the watershed are vulnerability and exposure. Therefore, the location of the collapse of the near-shore stream is the hot spot of landslide disaster, which has the characteristics of high TWI and SDR. Its high potential deposition and transport rate, in the event of a collapse, will result in huge debris and/or sediments, severely affecting it and downstream protected targets.

Disaster ratio is used to verify the accuracy of the model, and the validation results show that the determination coefficient of the model is 0.7535 with significance level of 1% (Fig. 15). The reason for the small change in disaster ratio is the watershed landslides caused by extreme rainfall, which leads to the occurrence of teleconnection phenomenon in the subdivisions. For example, if the upstream watershed collapses, the debris from the collapse may be deposited in the gully/stream, forming a dammed lake. If damaged, it will cause debris flow and endanger downstream protection objects. The model only considers the point-source migration of debris. If a landslide disaster is likely to hit a particular protection object, it is recommended that the concept of non-point-source migration in the selected target watershed be used to show the extent of the derived disaster in detail.

Fig. 15
figure 15

Relationship between derived disaster risk and disaster ratio

Full size image

4.5 Potential sediment disaster along the road

The risk level of the Tai-21 highway can be extracted using a subdivided derived disaster risk and roadmap (Fig. 16-left). The accuracy of the model was verified using information from ten sediment disaster sites destroyed by Typhoon Morakot on the Tai-21 highway (Table 4). Figure 16-middle is the distribution of disaster sites and newly formed bare land along the route. Figure 16-right is the collapse status of each disaster site.

Fig. 16
figure 16

Derived disaster risk for terrain subdivisions (left), the distribution of disaster sites (middle), and the collapse status of each disaster site (right)

Full size image
Table 4 Tai-21 Damage sections of Tai-21 highway caused by Typhoon Morakot (Huang 2014)
Full size table

Disaster sites 1 and 2 are located near the mainstream and can be classified as runoff attacks on slopes, causing roadbed damage rather than the type of disaster caused by rain-induced landslide, so the risk of landslide-derived disaster is low. The causes of disaster sites 3 and 4 are the same as those of sites 1 and 2, but the risk of disaster is moderate, and although also affected by stream runoff, the road sections are located upstream and are more likely to be affected by upstream landslide. Sections 5, 6, 8, and 9 are located in the high disaster risk, where the road is damaged by debris flow formed by upstream landslides, in line with the prediction of high-risk sections. Disaster site 7 has a higher risk than the surrounding section, and the roadblock here is caused by falling rocks on the slopes. Such disasters are small in scale and are mainly affected by the higher risk of primary collapse. In addition, the area of rock falling in the disaster area is small, limited by the resolution of satellite images and plant cover, so the scope of the disaster is more difficult to explain. The No. 10 disaster point is the road damage caused by the uphill landslide and is a high-risk section. The results show that the model can effectively predict the potential damage of debris flow and road slope collapses.

In order to facilitate early warning or management of roads based on disaster risk, the Tai-21 road mileage is mapped according to the disaster site of Typhoon Morakot (Fig. 17). Risk levels are divided into low, medium, high, and very high quartiles (Table 5). Most low- and medium-risk sections are located downstream and are less affected by landslides in the upper watershed. Sections with high and very high levels are located in the upper and middle reaches, where the collapsed debris moves downstream through the water network, and the closer the upstream, the greater the impact. However, due to the distance from the water network, landslides (primary disasters) caused by rainfall are difficult to affect downstream protection objects, and the risk of derived disasters decreases as the watershed boundary approaches. The eight disaster points that the model can accurately predict are high risk and above. The results show that once the risk of road disaster exceeds the median (Q50), the probability of sediment disaster is very high. The remaining two types of disasters are not landslides caused by rainfall, so the disaster risk level for such parts of this model is low to moderate.

Fig. 17
figure 17

Trend of derived disaster risks along Tai-21 highway

Full size image
Table 5 Risk level and resilience management at the disaster sites
Full size table

4.6 Resilience management

In general, the management of disaster sites can be restored based on engineering, ecological and social-ecological resilience. Engineering resilience is a minor disturbance caused by small-scale events, often beyond the system tolerance, which can be absorbed and restored through a single operation. Ecological resilience is the interference caused by mesoscale events, which requires organizations to coordinate with each other under the original structure, make effective use of resources and achieve a new balance. Social-ecological resilience is an unprecedented event that often affects systems beyond the original organization. Since the risk model takes into account the occurrence and scale of the primary disaster, it is easy to recommend post-disaster resilience levels at disaster sites based on the risk level of the model (Table 5). Pre-disaster disaster management can use the spatial distribution of disaster risk derived from the slope units of protected areas, identify the hot spots prone to disasters, and put forward concrete measures to improve the resilience of hot spots.

5 Conclusion

Roads are important protection objects in the watershed, and the places where the roads passed may face primary disasters and derived disasters. The model developed in this study is mainly based on potential sources of collapse, but the transportation routes and sinks of point-source sediment disasters are regulated and evaluated through topographic subdivision analysis. The accuracy of the initial model construction is based on grid resolution, and the spatial distribution of road disasters can only be analyzed through the subdivision of each road section. In addition, the derived disaster model is derived from the primary disaster models. Since primary disasters have been considered, the possibility of calculating derived disasters from the relevant subdivisions is more appropriate to discuss the possibility of slope disasters along the route.

In the face of extreme storm events under climate change, the prevention and control of sediment disasters in watersheds is an important subject. Potential sediment disaster hotspots in watersheds can be distinguished from sources, paths, and sinks. The spatial distribution between hotspots is directional, so the landslide location (source) of each slope unit is transported through a stream (path) and can be deposited (sink) in different watershed subdivisions. Because mountain roads span different watershed zones and face different types of landslide primary or derived disasters, the concept of multi-scale watershed zoning and telecoupling is a way to explore the potential sediment disaster on mountain roads. In addition to quantitative analysis of the possibility of sediment-derived disasters along the road, the feasibility of value-added application of early warning and resilience management were discussed using the concept of non-point-source, and road risk management strategies are proposed in this study.

Based on the level of risk provided in this study, sections of the road can be divided according to potential-derived disasters. Areas of high risk above this level can receive varying degrees of early warning prior to the occurrence of a disaster. High-risk areas can also be identified as disaster hotspots in advance, and disaster prevention and mitigation-related management measures should be formulated. The applied landslide-derived model takes into account the trade-offs between the risks and scale of landslide events and uses TWI and SDR indices based on watershed-scale water networks to provide quantitative information for early warning and disaster resilience management. Through the screening of disaster hot spots and the corresponding countermeasures for disaster management, it provides a reference for disaster prevention and mitigation measures of mountain roads.