1 Introduction

With the increasing effect of urbanization and climate change in recent times, urban floods are becoming more frequent and devastating (Hirabayashi et al. 2013; Duan et al. 2016). Especially Africa is the most affected region by floods next to Asia (CRED and UNISDR, 2015). Notably, poor communities in sub-Saharan African cities are disproportionately affected by urban floods, the latter being exacerbated by climate change (Douglas et al. 2008; Sliuzas et al. 2013; Perez Molina 2019). Therefore, there is a growing effort at national, regional, and local levels focusing on urban flood hazard modeling as part of integrated flood management (IFM) to cope with urban floods (Sy et al. 2016; Sy et al. 2020; Pérez-Molina et al. 2017). Strategies to cope with urban floods, such as adaptation and mitigation measures, require an urban flood hazard assessment, where a high-quality input dataset is essential for effective flood hazard modeling. Flood hazard is an analysis that combines hazard intensity with a return period or probability of occurrence. The intensity of floods is usually characterized as a combination of the extent and maximum water level. Unfortunately, it is rare that flood observations are good enough to derive a probability from observed floods. Therefore, the probability of floods is replaced by the probability of the driver, the rainfall, for which good records exist with global coverage. There are two steps concerning rainfall in a flood hazard analysis. The return period of extreme rainfall is calculated from daily rainfall records, based on maximum daily rainfall per year over a period of 20–30 years, on which extreme value distribution is applied (e.g., Gumbel distribution). It is important to note that the stakeholders often choose the return periods based on their capacity for disaster prevention and mitigation measures. The return periods and associated rainfall values are based on annual maximum 24-h rainfall. It is important to take these established maximum rainfall values as a starting point so that the results of any alternative method can be clearly related to flood mitigation activities.

However, the 24-h maximum rainfall is not enough for flood hazard assessment. A flood model needs rainfall with a high temporal resolution to accurately simulate flood dynamics in complex urban environments. Therefore, the second step is that design storms are used with a shape derived from probability density functions based on high-resolution rainfall data as close as possible to the area (see, e.g., Chen and Hill 2007; Balbastre-Soldevila et al. 2019)).

Design storms are developed initially to dimension drainage channels for peak discharge (Keifer and Chu 1957); but for flood hazard modeling, which depends on rainfall-infiltration dynamics (e.g., Chen and Hill 2007; Balbastre-Soldevila et al. 2019; Umer et al. 2019)), it requires more accurate design storms on the aspects of peak intensity and its temporal characteristics. Conventionally, in the areas where long records of observed rainfall with a high temporal resolution are available, design storms of a shorter duration are developed from the intensity-duration frequency (IDF) curves, using various methods such as the alternating-block method giving a slightly asymmetrical event (Guo and Hargadin 2009; Sun et al. 2019).

Both steps have inherent problems. The frequency-magnitude analysis is by necessity tied to a location where long observation records exist. These are scarce and often spatially biased toward airports and urban areas in general, where long records are commonly established. These locations may not be representative of flood-prone areas, and the spatial density of observations may not capture the spatial variability of the rainfall patterns. Similarly, not enough detailed data exist to establish IDF curves, essential for reliable estimation of design storms with higher return periods (e.g., T = 10, 25, 50, and 100 years) (Mugume and Butler, 2017). In such areas, the common practice is to use simplified procedures developed based on limited rainfall observations to provide a representative design storm of that region. For instance, Fiddes et al. (1974) developed a simplified method for predicting design storms of a given return period in East Africa, based on observed rainfall records ranging between 8–30 years. This results in a local flood hazard prediction based on a design storm that forms a generalized regional IDF curve, which is problematic. At the same time, weather phenomena that cause floods have spatial extents varying from relatively small convective storms to continental size phenomena such as monsoons.

One of the ways to gain insight into the spatial patterns of rainfall is using numerical weather prediction models. As their performance improves, these might serve as alternative rainfall data sources for producing optimal design storms required for flood hazard modeling in such a data-scarce area. A second source is high-resolution global; satellite data such as the Global Precipitation Measurement (GPM) and the Global Satellite Mapping of Precipitation (GSMAP) that provides 0.1 degrees 30-min rainfall estimates (Yang et al. 2020). In this study, we use the WRF model (Powers et al. 2017) to gain insight into the amount and distribution of rainfall events required for flash flood food modeling (e.g., Hong and Lee 2009; Leung and Qian 2009; Pennelly et al. 2014; Liu et al. 2015; Li et al. 2017; Chawla et al. 2018)). With the usability of the recently released high-resolution ERA5 reanalysis climate data as boundary conditions, the model can consider the large-scale atmospheric processes which can be linked to the high-intensity rainfall triggering flood events in the catchment (Giannaros et al. 2020; Greco et al. 2020). Moreover, the WRF model is able to consider the local-scale processes affecting the rainfall, such as the effect of urban extent and position on extreme rainfall distribution (Paul et al. 2018; Zhang et al. 2018; Oliveros et al. 2019). In the same way, the WRF model is robust in considering the variability of the storms across wide areas and its flexibility to reproduce rainfall data at the spatial and temporal resolution that can be needed for the flood hydrology model (Liu et al. 2012; Chawla et al. 2018; Tian et al. 2020). Thus, when appropriately configured and validated, the WRF model is a suitable tool for simulating the high-intensity rainfall events and spatial variability for flood modeling (Zittis et al. 2017; Sikder and Hossain 2018).

A recent study by Sikder et al. (2019) indicated the usability of the WRF rainfall simulations of moderate-intensity and high-intensity rainfall events for actual urban flood modeling in Houston, the USA. However, the WRF simulated actual rainfall events are not directly used for the flood hazard modeling. In the case of using actual rainfall products for flood hazard modeling, the magnitude of the gridcell events is spatially different, which creates a difference in the simulated flooding over the catchment; thus, challenging for flood hazard analysis. Hence, design gridcell rainfall events have to be created. However, there is no common way to convert the WRF simulated rainfall events into the design storm form essential for flood hazard modeling. Therefore, this study presents a new methodology to translate WRF simulated high-resolution convective rainfall events into design storms for flood hazard modeling. The performance of the WRF-based design storms is evaluated against existing alternating-block method design storms obtained from pre-established IDF curves in order to evaluate differences from the point of view of flood hazard assessment. The strengths and weaknesses of our proposed method are discussed with the potential need for further steps. As a study area, the rapidly growing city of Kampala is used, specifically, the northern Lubigi catchment where floods frequently happen in the former wetlands, where dense informal settlements (slums) exist (Sliuzas et al. 2013; Perez Molina 2019; Umer et al. 2019). The Kampala City council has adopted a 10-year return period as the basis for the improvement of the surface drainage system to cope with a certain level of flooding.

This article is organized as follow. The study area's description and the events chosen for the case study are described in Sect. 3. The study results on the constructed design storms and their comparison are presented in Sect. 4, then followed by results on the flood model and conclusion in Sects. 5 and 6.

2 Method

Figure 1 presents the framework we implemented to translate four WRF simulated high-intensity rainfall events (HIREs) into a given return period's WRF design storm. The four storms are chosen because flooding was reported in the study area on those dates, and they are different in duration, magnitude, and peak intensity. The framework illustrates the WRF design storm's (right-side) comparison with the IDF-based alternating-block method (IDF-AB) design storms. The IDF-AB design storms of 2- and 10-year return periods (hereafter ‘AB2yr' and ‘AB10yr') are compared with the WRF design storms that are expressed as the quantiles (explained below). The IDF-AB and the WRF design storms are compared and used as input for flood hazard modeling with the model openLISEM (Baartman et al. 2012; Jetten 2014; Umer et al. 2019).

Fig. 1
figure 1

The workflow of this study to construct design storms from WRF simulated gridcell-rainfall events and its comparison with design storms derived based on the alternative-block method, including their application for flood hazard modeling in the case study

Full size image

2.1 WRF model settings

WRF design storms are constructed based on the WRF simulated HIREs produced at the spatial resolution of 1 km. (The inner modeling domain is a rectangle represented by the gray color in Fig. 2.) The WRF model (version 4.1 (Powers et al. 2017)) was configured to simulate four known HIREs (i.e., 25 June 2012, 03 September 2013, 13 April 2016, and 16 April 2016) that have caused flooding in Kampala. For initial and boundary conditions, the ERA5 (Hersbach and Dee 2016) dataset was utilized. The model simulation and evaluation follow the MP-CP-PBL procedure introduced and discussed in (Umer et al. 2021), where M.P. refers to microphysics, CP-cumulus parametrization, and PBL is the planetary boundary layer. Accordingly, for 25 June 2012, the best combination is the double moment Marrison (M2) scheme combined with Grell-Freitas (G.F.) and ACM2. For 03 September 2013, it is WSM3 scheme with G.F. and ACM2, while for both 13 and 16 April 2016, the best combination is the WSM6 scheme with Kaint-Fritsch (K.F.) and ACM2. Detailed information on the parameterizations is in the WRF model manual (Skamarock 2008). The WRF model downscaling procedure consists of four domains with 27 km, 9 km, 3 km grid spacing as outer domains, and 1 km as the innermost domain, following the most recommended ratio of 1:3 by Liu et al. (2012). For each HIRE analysis, we considered only the model output in the innermost domain of WRF with spatial and temporal resolutions of 1 km and 10 min. The convective and independent model output event at 1 km and 10 min resolutions (hereafter gridcell event) is converted into design storms to serve as input for urban flood modeling.

Fig. 2
figure 2

Study area: Map of Kampala city with land use fraction derived from Landsat image, source (Abebe, 2013); Upper Lubigi catchment is used for flood modeling in this study; Kampala catchment; WRF domain is the innermost domain with 1 km spatial resolution that used for rainfall analysis

Full size image

2.2 WRF design storms

Following the WRF simulation of the selected HIREs, the method follows a two-step procedure. The assumption here is that all the gridcell events in the inner domain of WRF are considered separate, and spatially independent rain events as these events are highly localized due to their convective nature. This assumption implies that the extreme rainfall events that trigger localized urban floods are often related to certain weather conditions that are highly variable in space. WRF model result at 1 km spatial resolution is assumed to capture the spatial variability of the extreme precipitation related to these weather conditions (Umer et al. 2021). Therefore, a strategy to capture this spatial variability of extreme rainfall events is to consider each gridcell as a virtual rainfall station for design storm construction.

2.2.1 Step 1: selection of potential gridcell events

The grid cell rainfall events that have the potential to cause flooding are selected based on existing local rainfall information to serve as an area-dependent threshold. For this case study, the threshold is based on the depth and peak intensity of a 2-year return period storm for Kampala, estimated from the frequency analysis of daily rainfall in Kampala (Mugume and Butler 2017). This is considered the minimum event that triggers local floods in the former wetlands and flood plains. As such, the city's flood lines and drainage system are designed for events of 2-year or more (KCCA 2010). Therefore, the gridcell events in the innermost domain of WRF are identified and selected if they fulfill both criteria:

  • For moving storms, select grid cells with a total rainfall amount equal to or exceeding 2-year return period, and

  • Select grid cells with the peak intensity equal to or exceeding the peak intensity of 2-year return period

2.2.2 Step 2: selection of representative gridcell events

To select the representative gridcell events to define the WRF design storms, we summarized the distribution of the potential grid cells into quantiles following a two-stepped procedure. Initially, we examined the cumulative distribution functions (CDF) for each of the four considered rainfall events and each potential grid cell selected under step 1. We extracted the maximum value from each CDF in the second step and calculated its probability density function (PDF). As a result, we focused on the total rainfall amount for each HIRE and examined its spatial distribution for each potential grid cell. We computed three quantiles from the calculated PDFs, with probabilities p = 0.025, 0.5, and 0.975. In this way, we aimed at extracting a sample from the bulk of the distribution (median) and the expected variability associated with it (95% confidence interval or the range between the left and right tails of the distribution). We assume that each quantile represents a design storm. For each of the three quantiles (hereafter the WRF design storms), the storm events are expressed in terms of their properties such as rainfall amount, peak intensity, and the time dynamics, which mainly include the time to peak intensity and the elapsed time for the derived cumulative rainfall.

2.3 IDF design storms

To investigate the performance of the constructed WRF design storms, we compared them with the classically derived IDF design storms known as alternating-block design storms. The steps to obtain design storms from the IDF curves are divided into two. The first step is frequency analysis of the daily (24-h) point rainfall depths for various return periods. In this case, we used the estimated rainfall depth of Kampala from the literature, as indicated by (Fiddes et al. 1974) (Mugume and Butler 2017) (KCCA 2010). The second step is to convert the 24-h rainfall depth of different return periods into the shorter duration design storms, using the so-called alternating-block method. We adopted a similar approach as discussed by Mugume and Butler (2017) and applied Eqs. 1 and 2 for constructing the IDF design storms.

$${I}_{R}= \frac{a}{{\left(t+b\right)}^{c}}$$
(1)

where IR. (mm/hr) is the maximum intensity corresponding to a rainfall duration t, and a, b and c are constants. By eliminating ‘a’, Eq. 1 can be simplified into Eq. 2.

$${R}_{T}={\frac{t}{24}\left(\frac{24+b}{b+t}\right)}^{c}*{R}_{d}$$
(2)

where RT is the rainfall depth for any duration, t, Rd is the 24-h rainfall depth for different return periods. The extracted design storms representing T = 2 and T = 10 years return period were used as a reference to compare with the design storms constructed based on the WRF simulated HIRE. The WRF and standard IDF-based design storms are independent in terms of data used and the method followed, but both produce rainfall properties of a given storm that can be used for flood hazard modeling. For comparison purposes, the two design storms are constructed for the same duration (2 h) and time aggregation (10-min), which is essential to make a fair comparison. The purpose of this comparison is mainly to see how the WRF design storms' rainfall properties determining the flood hazard characteristics evolve compared to that of the standard IDF design storms. The detailed statistical characteristics and derivation of the parameters in Eq. 2 are less important and beyond the scope of this study.

In this study, the IDF design storms of T = 2 and 10 = years are compared with the WRF design storms expressed as the three quantiles visually in terms of their total rainfall amount (mm), peak intensity (mm/h), and the time dynamics. All design storms are defined with the time aggregation of a 10-min interval, and also, to make a fair comparison, all design storms are considered the total duration of 2 h. In Eq. 2, we used the 24-rainfall depth reported by KCCA (2010) (described in Sect. 3.2). As the design storm duration is considerably reduced (i.e., from 24-h to 2-h duration), the resulting rainfall depth is also reduced, resulting in lower rainfall depths for both return periods than the actual rainfall depth of 24-h duration. The constants in Eqs. 1 and 2 are taken from Fiddes et al. (1974), who at that time had only a few years of data regarding the whole of east Africa. Fiddes et al. (1974) used a wider area to get the constants ‘b’ and ‘c’, and so they may be area representative but not for Kampala specific. Moreover, the constants are to be derived from sub-daily observations to extrapolate 24-h rainfall to the part of the curve that is highly non-linear. However, in the absence of detailed long-term sub-hourly observed data, the same procedure can be followed and used the existing constants to construct the IDF-AB design storms of 2 and 10 years.

2.4 OpenLISEM flood model

To analyze the applicability of the constructed WRF design storms for flood hazard simulation, we used an event-based-integrated flood model called openLISEM (Baartman et al. 2012; Jetten 2014; Umer et al. 2019). The model is an integrated spatial hydrological model that simulates infiltration excess runoff for extreme rainfall events and shallow floods in urban and rural catchments (Habonimana 2014; Nurritasari et al. 2015; Pérez-Molina et al. 2017). OpenLISEM is able to simulate physical processes leading to floods at very detailed temporal resolution (0.1 to 60 s) for catchments from 1 ha to several 100 km2 with typical spatial resolutions between 5 and 20 m (Bout and Jetten 2018; Bout et al. 2018). The model's hydrological processes include rainfall inception by vegetation cover and storage by roofs before reaching the ground. Once reaching the ground, the net rainfall is infiltrated using the Green and Ampt model, considering different surfaces such as impervious, compacted, and vegetated soils characterized as fractions of a gridcell. Infiltration excess is first stored because of surface roughness, and when that overflows, the surface runoff is simulated using a finite volume solution for 2D st Venant flow (Bout et al. 2018). In the implementation of this study ((version 5.9, 2020), openLISEM does not differentiate between overland flow and flooding, except the (user-defined) critical water depth. When the overland flow reaches a channel or stream, discharge is generated using a kinematic wave applied to the channel network. A detailed description of the model flow approximation is given in (Delestre et al. 2014; Jetten 2014; Bout and Jetten 2018). The critical water depth considered in this study is arbitrarily set at 0.1 m to distinguish between flooding and overland flow. The arbitrary critical depth is set because a flood is assumed to be all water that is deeper than a user-defined value. The user-defined model gridcell value that we consider as a flood can vary from place to place and be decided based on the knowledge of the area. In our case, water deeper than 0.1 cm was considered a flood, which was decided after discussing with stakeholders in flooded areas in the northern Lubigi catchment.

The openLISEM model was calibrated for the upper Lubigi catchment using discharge figures extracted from the drainage projects of 2002 and 2010 (Sliuzas et al. 2013; Pérez-Molina et al. 2017) field observations and interviews with the residents on past flood impacts (from Oct. 2012) (Chogyal 2013; Habonimana, 2014). This calibration used observed high temporal resolution single extreme event of 25 June 2012, surveyed channel dimensions, and terrain characteristics derived from elevation data. The land cover effects, including the fraction of buildings, vegetation cover fraction, and bare soil fraction, were extracted from land cover maps derived from Landsat images, as described by (Pérez-Molina et al. 2017; Perez Molina, 2019; Umer et al. 2019). Soil data determining infiltration processes were obtained from the soil grids database following the procedure indicated in (Umer et al. 2019). The current simulation is the extension of the previous studies by (Perez Molina, 2019; Umer et al. 2019), changing only the rainfall event used for flood hazard modeling. Hence, the openLISEM model is set up at the upper Lubigi catchment, Kampala, with the constructed design storms to simulate the flood hazard. Other model input data, such as land use fraction, soil properties, and channel dimensions, were kept the same for all simulations.

In order to evaluate differences from the point of view of flood hazard assessment, the derived design storms (i.e., nine from WRF and two from the alternating-block method) are then used as input to the openLISEM hydrologic model for flood hazard modeling. The constructed design storms are used as a tabular form for the flood model, and the other model input will be kept the same throughout the simulation. The flood model result will be analyzed in terms of flood hydrographs, flood extent maps, flood depths, and structural damage using the model results from the alternating-block method as a reference. The simulated flood hydrograph analysis at the main outlet is essential to understand whether the channel size is sufficient to drain a peak flood of each design storm compared to the existing channel capacity. The analysis of the results in terms of flood extent and flood area is also useful to understand better the urban footprint exposure to the flooding triggered by different design storms. To emphasize the applicability of the WRF design storms in terms of flood exposure, the comparison in terms of structural damage will also be carried out by considering Kampala's average building size of 90 m2 (Sliuzas et al. 2013).

The WRF design storms' appropriateness in simulating the flood extent will be compared with the results from the IDF-AB flood model results through pixel-by-pixel comparison using F statistical measures, which has been used in many flood extent studies (Schubert and Sanders, 2012; Yan et al. 2014; Amarnath et al. 2015). Specifically, the simulated flood extent maps using the WRF design storms are compared with AB2yr/AB10yr using a simple aggregate performance measure, F, following a similar procedure presented in several flood extent studies (Aronica et al. 2002; Horritt and Bates, 2002; Amarnath et al. 2015). The F is calculated as:

$$F=\frac{A}{A+B+C}$$
(3)

where ‘A' is the number of cells correctly predicted by both WRF design storms and the AB2yr/AB10yr; ‘B' is the number of cells predicted as flooded with WRF design storms that are simulated non-flooded by the AB2yr/AB10yr (overestimation); and ‘C' is the number of cells simulated as non-flooded with WRF design storms that are simulated as flooded with AB2yr/AB10yr (under-estimation). The F performance measure is applied here to investigate the WRF design storms' appropriateness for flood extent modeling compared to AB2yr/AB10yr based on the aggregated score, which varies between 0 and 1; a higher value is better.

3 Case study

We choose Kampala, the capital city of Uganda, as a case study to test the method. The city is an ideal location to test the method because it is one of the sub-Saharan African city's frequently affected by flooding. At the same time, the lack of high-quality rainfall data hinders the proper flood hazard modeling for managing this recurrent flooding. Advances in the methodology, such as the one introduced in this study, to utilize the low-cost model output data for flood hazard modeling, are essential to make the city more resilient.

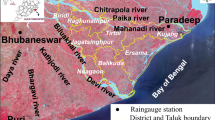
The city is located near Lake Victoria at the central latitude of 00 ′19' N and longitude 320 ′35' E and has about 350 km2 total area (see Fig. 2). The high-intensity rainfall events are mainly influenced by the inter-tropical convergence zone (ITCZ) and the topography of the Lake Victoria basin, triggering localized flooding in the city (Pérez-Molina et al. 2017; Umer et al. 2019). Urban flooding in the city is aggravated by the unplanned urban expansion in former wetlands and poor drainage management of the surrounding hills (Douglas et al. 2008; Sliuzas et al. 2013). High-intensity rainfall events frequently cause storm runoff, which surpasses the limited city infrastructure's capacity and triggers localized flood events. Consequently, causing estimated annual damage between the U.S. $1.3 million and the U.S. $7.3 million and is expected to increase under changing climate conditions (Taylor et al. 2015).

The study area considers the upper Lubigi catchment (polygon represented by the yellow color in Fig. 2) within Kampala city as a case study to investigate the applicability of the constructed WRF designs storms for flood hazard modeling. The catchment's currently functioning drainage system was designed and implemented based on the 2002 and 2010 masterplan (KCC 2002; KCCA 2010). According to the master plan, the primary drains' (i.e., the widest channels draining the main valleys) and the former wetlands are canalized and widened. At the same time, narrow culverts are replaced by a series of large box culverts to drain a peak discharge of about 67 m3/s, which represents the 24-h duration design storms of a 10-year return period (Sliuzas et al. 2013). The master plan reported that the secondary and tertiary drainage systems were designed to accommodate the flood peak of a 2-year event. The Upper Lubigi catchment is chosen for this case study because it represents an urban catchment where ground data essential for flood hazard modeling is available through the regular project and MSc fieldwork in collaboration with Makerere University (Sliuzas et al. 2013; Habonimana 2014; Rossiter 2014; Pérez-Molina et al. 2017).

3.1 Selected events

Four storm events that have caused flood hazards in the city were used to test the developed methodology. The first convective storm event occurred on 25 June 2012 with an observed daily total rainfall amount of 66 mm (a typical 2-year return period event). An automatic weather station (AWS) in the city indicated that the event lasted for only 1 h and 30 min. The second storm occurred on 03 September 2013, with total daily rainfall of 52 mm. The third and fourth events occurred in the main rainy season on 13 and 16 April 2016, with 46 and 44 mm total rainfall recorded at the standard rainfall station.

This study used two rainfall data sources. These are observed daily rain gauge data (Fig. 2) and satellite rainfall estimation from Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS) (Funk et al. 2015). Sub-daily rainfall data from AWS are available only for the 25 June 2012 storm. Thus, for consistency, the WRF model evaluation is only conducted by using daily rain gauge data collected from the WMO global daily summary of the day. CHIRPS data are available at a daily time step and spatial resolution of 5 km, and it is used as the areal average of the grid value extracted to the WRF innermost domain. In contrast, a comparison of WRF simulation with the gauging station is carried out with respect to the grid value at the gauging location.

3.2 Existing IDF curves

In this study, the existing design storms of 2- and 10-year return periods are obtained from Kampala's pre-established IDF curves. The pre-established IDF curves of Kampala are derived from rainfall depths of different return periods following the procedure illustrated by (Mugume and Butler 2017), and it presents the graphical illustration of the relationship between rainfall intensity (mm/h) and duration (h) (Fig. 3).

Fig. 3
figure 3

Pre-established intensity–duration–frequency curves for Kampala, Source: (Mugume and Butler 2017); the curves show that large variations in rainfall intensities occur at rainfall durations less than 4 h for all return periods. Our current study will derive design storms with a rainfall intensity duration of 2 h to comply with the rainfall intensity duration of the WRF simulated events

Full size image

Table 1 shows the daily (24-h) point rainfall depths for various return periods as collected from the literature. Mugume and Butler (2017) reported that rainfall depth of 2-year return period is determined using the annual maximum series method, and then, a generalized Gumbel equation is applied to determine the 24-h point rainfall for the 10-year return period. The derived rainfall depths for the respective return periods are different, mainly because of the observed rainfall's short records and the applied methods. For the WRF design storms criteria (Sect. 2.2.1), the minimum rainfall depth of 60 mm is used as a cutoff threshold, where 100 mm/h is the maximum peak intensity belonging to a rainfall depth of 60 mm. KCC (2002) is adopted for deriving the IDF-based design storms using Eqs. 1 and 2 because the city's flood plain maps and drainage systems are built based on these design storms.

Table 1 The derived 24-h point rainfall depth of Kampala for different return periods (source, (KCCA 2010), considered observed years 36; (Mugume and Butler 2017), considered observed years 51
Full size table

4 Results of design storms

This section presents the results on the developed design storms from two main aspects: (1) the results of WRF design storms derived through the representative gridcell events, and (2) the comparison of WRF design storms with that of the alternating-block method in terms of their rainfall properties.

4.1 WRF design storms

4.1.1 Simulated high-intensity rainfall events

Four HIREs used for design storm construction are simulated using the optimum WRF parametrization combinations (Umer et al. 2021). The simulated daily precipitation for the inner domain of WRF at 1 km spatial resolution is shown in (Fig. 4). During events in the non-main rainy season (i.e., 25 June 2012 and 03 September 2013), patchy rainfall occurs over the catchment, where events in the main rainy season (i.e., 13 and 16 April 2016) show a relatively evenly distributed rainfall over the catchment.

Fig. 4
figure 4

Simulated 24-h rainfall amount for four different events in the innermost domain of the WRF model. The insets in the bottom-right corner are the subtractions of the 24-h accumulated rainfall simulations from that in the CHIRPS observation

Full size image

Table 2 compares the simulated 24-h rainfall amount with the gauging station and CHIRPS in the inner domain of WRF. For 25 June 2012 and 03 September 2013, the simulated grid cells 24-h rainfall amount at the gauging location is very low, with the differences between the observation and simulation of about + 43 and + 33 mm, respectively. The big difference between the observation and simulation rainfall amount at the gauging location is attributed to the simulated events' sparse distribution. The heterogeneity in the simulated events in this season is also indicated by the lower area-averaged rainfall differences between simulation and CHIRPS. The rainfall events in the non-main rainy season are mainly influenced by the mesoscale convective system (e.g., Lake Victoria topography), which results in patchy rainfall over the catchment.

Table 2 Comparing WRF rainfall with the stations and CHIRPS rainfall for the best physics combinations simulated for four different rainfall events caused floods hazard in Kampala, Uganda
Full size table

In contrast, in the case of 13 April 2016 and 16 April 2016, the simulated grid cell's 24-h rainfall amount at the gauging location is close to the observation with the differences of 2.6 and 6.5 mm, respectively. The areal-averaged rainfall amount for 13th and 16th April 2016 is 46.5 and 27.2 mm, which is much higher than the CHIRPS amount. Compared to the CHIRPS, the higher areal-averaged rainfall amount indicates the relatively uniform gridcell-rainfall amount simulated over the catchment. It suggests that the prevailing weather is more of a synoptic-scale system. Hence, the simulated rainfall amount distribution is relatively homogeneous, covering more areas than the events that occurred in June and September (Fig. 4).

4.1.2 Potential grid cell selection

Step 1 in constructing a WRF design storm is to identify the potential gridcell events that can cause the flood hazard. We considered only WRF grid cells in the inner domain with the storm's total rainfall amount above 60 mm and a peak intensity equal to or above100 mm/h, following the criteria introduced in Sect. 2.2.1. Figure 5 shows the relationship between the simulated storm's total rainfall amount and peak intensity for the four different events in the inner domain of WRF. As shown in the figure, we have four locations considering 60 mm of rainfall amount and 100 mm/hr of peak intensity as the standard point: upper and lower left, and upper and lower right.

Fig. 5
figure 5

Relationship between storm's rainfall amount and peak intensity for four different events considered in this study; the points in the upper right are used for design storm analysis; hence, the 03 September 2013 event is not used for this study (see text). Each dot is a gridcell within the inner domain of WRF

Full size image

The upper right of each graph in (Fig. 5) represents grid cells during the storm with total rainfall amount and peak intensity equal to 60 mm or 100 mm/hr. The grid cells in the upper right are the potential grid cells selected for WRF design storm construction and are described in the next section. The upper left's grid cells have a high rainfall volume but a peak intensity of less than 100 mm/h. The rainfall events in this area can cause the flood, but possibly with a slower response and with a lower flood peak. The lower left represents grid cells during these four events with the lower rainfall amount and intensity. Therefore, this area represents too little rainfall to trigger the urban flood for the desired return period. The lower right location represents grid cells of these four events with rainfall amounts lower than 60 mm, but higher rainfall intensity above 100 mm/h. The rainfall in this location represents short-duration, high-intensity events and can be very important for flood control elements such as culverts. The numbers of potential gridcell events that fulfill the criteria and are then selected for design storm construction are 6, 43, and 45, for 25 June 2012, 13 April 2016, and 16 April 2016, respectively, while the 03 September 2013 event is excluded as zero grid-cells fulfilled both criteria.

4.1.3 Representative grid cell selection

In the second step, to select the representative gridcell events in the upper right that are used to define the WRF design storm, we used a quantile expression of the cumulative rainfall event (see Sect. 2.3.2). Figure 6 summarized the corresponding results for the three remaining HIREs. As shown in the top row figures, the probability density functions (PDFs) show a near-Gaussian distribution only for the 13 April 2016, whereas for the events on 25 June 2012 and 16 April 2016, the distributions appear bimodal and positively skewed, respectively. The different distribution shapes indicate that: 1) the gridcell rainfall simulated on the 25 June 2012 has two peaks, one at around 62 and one less prominent, at around 74 mm; 2) the bulk of the grid cell rainfall amount on the 13 April 2016 is centered around 75 mm, with a near-symmetrical decay to the left and right tails; 3) the rainfall amount on the 16 April 2016 is light-tailed, with a central tendency at around 64 mm and a rapid decay to 100 mm. The implications of these characteristics in our analyses mainly involve the choice of how to represent these shapes. In fact, symmetrical or near-symmetrical distribution, and to some extent, also a binomial shape would have been suitably represented through two parameters typical of a Gaussian distribution, mean and standard deviation. However, this two-parameter type would have misrepresented the third case, where the light-tailed rainfall distribution would not allow for a symmetrical parameterization. In turn, we have opted to accommodate these differences in PDFs by using a quantile expression of the three distributions. The bottom row in Fig. 6 shows the cumulative distribution functions (CDF) for the three considered rainfall events are. The quantiles Q = 0.025, Q = 0.50, and Q = 0.975 are highlighted as gray lines in 6 and are considered representative rainfall events defined as the WRF design storms.

Fig. 6
figure 6

The results of quantile function: (Top) Density distribution; (bottom) cumulative curves of the gridcell events with the storms' rainfall amount equal or exceeding 1-in-2 year return period event. Each line in the bottom graphs represents the time series of the dots in (Fig. 4). The gray lines represent percentiles of the total rainfall amount: the smoothed gray line represents the median, the dotted gray line represents the lower quantiles, and the dashed gray line represents the upper quantiles

Full size image

Following this quantile expression, we have defined nine WRF design storms, i.e., quantiles per event. For simplicity, the acronyms for the WRF design storms are as follows: lower quantiles (hereafter ‘WRFL’), median (hereafter ‘WRFM’), and upper quantiles (hereafter ‘WRFU’). Hence, each event's WRF design storms are acronymed as WRF1L, WRF1M, and WRF1U for 25 June 2012, WRF2L, WRF2M, and WRF2U for 13 April 2016, and WRF3L, WRF3M, and WRF3U for 16 April 2016.

4.2 Comparing design storms

To compare the WRF design storm with the IDF-AB alternating-block method design storms, we considered three properties of the developed design storms as relevant: the total rainfall amount (mm), peak intensity (mm/h), and time dynamics. Time dynamics are the peak intensity's temporal characteristics, which include the time to peak intensity and the elapsed time for the derived cumulative rainfall. These rainfall properties are summarized in Table 3 and (Fig. 7), including the IDF-AB design storms' properties.

Table 3 Basic properties of the design storms constructed using WRF and the alternating-block method
Full size table
Fig. 7
figure 7

Constructed design storms: peak intensities and cumulative curves for WRF and alternating-block design storms. Cumulative curves for AB2yr and AB10yr events are overlapped

Full size image

4.2.1 Cumulative rainfall

Cumulative rainfall amount is the leading property that characterizes the constructed design storms. As shown in Table 3, the derived total rainfall depth for T = 2 and 10 years events (i.e., ‘AB2yr' and ‘AB10yr') is 58.2 and 91.7 mm. The result shows that compared to AB2yr, the total rainfall amount is overestimated for all cases that is by + 10% for WRF1L, + 7% for WRF2L, and + 3% for WRF3L. For all three WRF simulated HIREs, the total rainfall amount for WRFM is also higher than that of AB2yr but slightly lower than that of AB10yr. In the case of WRFU, the total rainfall amount is within a range of 16–35 mm compared to that of the AB2yr storm, which indicates that the WRFU result is about half higher than that of the AB2yr event. Compared to AB10yr, the total rainfall amount for WRFL and WRFM is considerably lower. The result shows that compared to AB10yr, the total rainfall amount is underestimated by −23% for WRF1U and −12% for WRF2U, but overestimated by + 0.2% for WRF3U.

4.2.2 Peak intensity

As Fig. 7 shows, the derived peak intensity for AB2yr and AB10yr is 111 and 175 mm/hr. The WRF design storms' peak intensities vary between 103 mm/h for WRF2L to 209 mm/h for WRF3U mm/h, which are relatively close to that of AB2yr and AB10yr, respectively. Compared to AB2yr, WRF3L overestimated by peak intensity by + 18%, but underestimates the peak intensity for WRF1L and WRF2L, with the differences of −6% and −8%, respectively. The result also shows that compared to AB10yr, the WRF1U and WRF2U underestimate the peak intensity by −65% and −29%, but overestimated for WRF3U by + 18%. The discrepancies between the WRF and IDF-AB design storms are partly due to WRF model simulation uncertainty as well as the poor quality of IDF-AB design storms to represent the spatial distribution of the storm over the city.

4.2.3 Time dynamics

The third relevant property of the constructed design storm is the derived peak intensity's temporal characteristics, including the time to peak intensity and the elapsed time for the derived cumulative rainfall (Fig. 7, bottom row). As shown in the figure, the peak intensity for IDF-AB design storms is attained at the center of the total duration. One of the IDF-AB design storm characteristics is that the derived peak intensity is attained at the center of the storm duration, which does not resemble the simulated events, particularly considering the convective storm with peak intensity reach immediately after the events. Notably, for all WRF1 design storms, the maximum intensity is reached 20–40 min earlier than the alternating-block design storms. Similarly, for WRF2 and WRF3, the peak intensity attains its maximum about 10–20 min before the alternating-block design storms. While this may not be important for flood hazard analysis, it may be relevant for early warning studies, where time to peak rainfall and peak discharge is essential.

The design storm temporal pattern can also be analyzed by comparing the cumulative rainfall depth and elapsed time expressed as the percentages (Fig. 7, bottom row). As shown in the figure, the pattern of all design storms is similar. The nearly leveled slope represents the beginning and ending section of the storm, connected with a sharp rise in the center, representing a higher rainfall intensity and a significant portion of the total rainfall amount. For most WRF design storms, the total rainfall amount of more than 60% occurs between 30 to 50% of their duration, which is higher than the IDF-AB, in which over 50% of rainfall amount occurs between 50 to 70% of its duration.

5 Results of flood hazard modeling

To investigate the WRF design storms' effect on flood hazard modeling, we used the nine design storms as input for the openLISEM model. The model results produced by using AB2yr and AB10yr are used as a benchmark. The flood model outputs are discussed in terms of flood hazard characteristics, including flood hydrographs, flood extent maps, flood areas, and flood impact on the number of buildings.

5.1 Flood hydrograph

Figure 8 shows the resulting hydrographs at the Lubigi catchment outlet for 11 design storms. As shown in the figure, a similar low peak discharge is obtained when using AB2yr as well as the WRFL (design storm with the lower total rainfall amount and peak intensity. In contrast, the highest peak discharge is obtained when using the AB10yr and WRFU design storms, which have a higher total rainfall amount and peak intensity. In particular, a flood peak obtained at the catchment outlet when using WRF3U is about 70 m3/s, which is above the reference flood control structure's capacity (i.e., 67 m3/s).

Fig. 8
figure 8

Hydrographs at the catchment outlet: From left to right: WRFL versus AB2yr and AB10yr; WRFM versus AB2 and AB10yr; and WRFU versus AB2yr and AB10yr. The dashed horizontal line represents the reference discharge of 67 m3/s

Full size image

5.2 Simulated flood extent

Table 4 shows the calculated F scores for the simulated extent of the flood for 9 WRF design storms benchmarked with AB2yr and AB10yr. Compared to the AB2yr event, WRF1L, WRF2L, and WRF3L produce a better flood extent with higher F scores of 0.87, 0.94, and 0.94, respectively. Compared to AB2yr, WRFUs overestimate the flood extent, which results in a lower F score (Table 4, first row). Considering the AB10yr event as a benchmark, WRF1M, WRF2U, and WRF3U produce a better flood extent with higher F scores of 0.85, 0.89, and 0.91, respectively. Compared to AB10yr, WRFLs underestimate the flood extent, which results in lower F scores (Table 4, second row). As shown in the table, the aggregate score decreases as we go from left to right (i.e., from WRFL to WRFU) when comparing with AB2yr and vice-versa when comparing with AB10yr. The results indicate that for WRFL, the comparison with AB2yr is more appropriate, while for WRFU, the comparison with AB10yr is more appropriate.

Table 4 Model results of flood hazard characteristics in the Upper Lubigi catchment in Kampala: (1) & (2) Performance measures, F score, of WRF flood extent benchmarked with alternating-block design storms; (3) calculated total flooded area based on water deeper than 10 cm; (4) number of structures (buildings) affected by flood deeper than 10 cm calculated based on an average structure size of 90m2
Full size table

5.3 Flood depth

In order to verify the applicability of the WRF design storms in producing flood depth maps used for flood hazard analysis, we compare flood depth maps produced when using the 9 WRF design storms with the results when using the IDF-AB storms based on a visual comparison of the maps. Figure 9 shows the depths of food water in the catchment area produced when using the WRF and IDF-AB design storms. As shown in the figure, following the topography of the catchment area, the low-lying areas and wetlands are flooded when using all design storms with flood depths varying between 0.5 to 2.6 m. However, as we go from WRFL to WRFU or as the return period increases, so too do the flood depths, as would be expected. Thus, maximum water depths of 2 m and above are simulated when using WRFU and AB10yr. The results are compatible with previous studies in the catchment (Sliuzas et al. 2013; Umer et al. 2019), whose results indicated that the wetlands of the catchment are fully flooded with design storms of typical 2-year events or more.

Fig. 9
figure 9

Flood depth maps based on model output using the alternating-block design storms for 2- and 10-year return periods (AB2yr and Ab10yr) and WRF design storms for three different events overlaid with a building hillshed. The red circles show two locations relevant for model results comparison. Location a the comparison between WRFL versus AB2yr, b the comparison between WRFU versus AB10yr

Full size image

In Fig. 9, red circle a, we showed the relevant location used for comparison of WRFL versus AB2yr. When using all WRFL, the simulated flood depths are between 1.5 and 2 m, but with AB2yr, the flood depth is between 1.0 and 1.5 m at the same place, which is due to the lower cumulative rainfall amount of AB2yr compared to that of WRFLs. In comparing WRFU with AB10yr (at circle b), the simulated flood depths are above 2.0 m in all cases. However, the number of grid-cells flooded with flood depths of greater than 2.0 m is more in the case of WRF3U compared to AB10yr.

As the intensity for the flooding is often expressed as the maximum depth at any grid-cell, a frequency distribution of that would be directly interesting for flood hazard analysis. Toward this, we produced the histogram of the water depths versus its frequency and compared the flood depths differences at any grid-cell when using the WRF and IDF-AB storms. As a showcase, flood depth differences per grid-cell between the WRF3 design storms and the IDF-AB storms are given in Fig. 10. As shown in the figure, for WRF versus AB2yr (Fig. 10, top row), the results with WRF flood depths are slightly higher; hence, the histogram differences are skewed in the positive x-direction. However, when comparing WRF versus AB10yr, except for WRF3U, the histogram differences in water depths are negative. For instance, in the case of ‘WRF3L—AB2yr', the flood depths differences per grid-cell are concentrated around zero with the frequency of 90%, while for ‘WRF3U—AB2yr', the flood depths difference is greater than zero and the frequency around the zero value is 40% with its distribution spreads toward the positive x-axis. The figure also shows that the WRF results have little bias/slight overestimation of flood depths when using the lower and median quantiles and large differences of flood depths when using the upper quantile design storm with respect to AB2yr. The figure also shows that the flood depths when using WRF are underestimated at WRF3L and WRF3M and slightly overestimated water depths at WRF3U with respect to the AB10yr. It is important to note that the maximum flood depths differences per grid-cell for ‘WRF3L—AB2yr' and ‘WRF3U—AB10yr' is less than 0.2 with frequency distribution concentrated near-zero value, which indicates that the WRFL and WRFU design storm can be relevant for 2-year and 10-year return period flood hazard assessment, respectively.

Fig. 10
figure 10

Frequency distribution (%) of the differences between the flood depths (meter) per grid-cell from the flood depth maps produced using WRF minus the IDF-AB design storms for the case of 16 April 2016 (WRF3)

Full size image

5.4 Effects of flooding on buildings

To analyze the applicability of the constructed design storms for flood hazard modeling, we also compared the results in terms of flood effect on the building. The effect of the flood extent on the building is calculated considering the building's areal density of 90 m2. Table 4, row 4, shows the number of building affected by the flood extent (water depth > 0.1 m) when using 11 design storms. Notably, the number of buildings affected by the flood extent when using WRF1L, WRF2L, and WRF3L are 5058, 4425, and 4777, respectively, slightly higher than when using AB2yr (i.e., 4258). In contrast, more buildings are affected by flood extent when using AB10yr (7258) and WRFU (i.e., 5761, 6299, and 8223 for WRF1U, WRF2U, and WRF3U, respectively), which is characterized by higher total rainfall amount and peak intensity. In all cases, the number of buildings affected by flood extent is well correlated with the inundated areas (see Tables 4, 3rd Row).

Moreover, model results also indicated that for all 11 design storms, the number of buildings affected by the flood is more at lower water depth (i.e., 0.1–0.5 m) and less at higher water depth (i.e., depths > 0.5 m) (see, Fig. 9). For instance, due to the flood depth ranges 0.1–0.5 m, the number of affected buildings is 3–9 times higher than at flood depths > 0.5 m. These results show that the maximum flood depth is more confined in the non-built-up areas represented by wetlands, consequently less effect on built-up.

5.5 Discussion

The study presents a new method to get a location-specific design storm based on WRF simulated high-intensity rainfall events, which proved to be suitable for flood hazard modeling in the data-scarce area. The method presented is flexible as it can be based on any desired combination of event magnitude and peak intensity. The magnitudes can be based on disaster mitigation plans of the stakeholders in the areas. However, while the magnitude is relatively straightforward to derive from a Gumbel analysis, the peak intensity may not be well known. A peak intensity could come from high-resolution rainfall measurement, or in the absence of that, from satellite imagery (30-min intensity) or even an IDF curve analysis. All of these have associated uncertainty.

Rainfall and satellite measurements may not have long-time high-quality records for constructing valid IDF curves. Selecting a characteristic peak intensity is less evident when time series are not very long. Besides, the construction of valid IDF curves relies on sub-daily storm data. Peak intensity can also be derived from satellite imagery, and for instance, GPM-IMERG has a 30-min time interval with global coverage dating back to the year 2000. Therefore, the time series derived from these images is already 20 + years, which means it's possible to construct design storms from this dataset. However, while aggregated values (3-day and weekly totals) show good agreement with ground measurements, the 30-min intensities do not generally show a high correlation (Fang et al. 2019; Chen et al. 2020), hindering its application for flood hazard modeling.

In this study, the data to get designs storm are based on WRF rainfall products simulated at high spatial–temporal resolutions to capture localized storm events. The WRF model is robust and flexible in reproducing rainfall data at the spatial and temporal resolution that can be needed for the flood hydrology model (Liu et al. 2012; Chawla et al. 2018; Tian et al. 2020). Here, we simulated four known events (i.e., 25 June 2012, 3 September 2013, 13 April 2016, and 16 April 2016) that have caused distinct flood hazards in Kampala, Uganda. For design storm construction, we used high-intensity rainfall output of the innermost WRF domain. Compared to the observation, the performance of WRF in simulating the storms is reasonably good enough to proceed with the results for design storm construction (Umer et al. 2021). Due to the patchy rainfall pattern on 25 June 2012, fewer potential grid cells were considered compared to 13 April 2016 and 16 April 2016. Moreover, model simulation for 03 September 2013 was unable to procedure the potential grid cell rainfall events certified for design storm construction. This result indicates that applying the developed approach requires an appropriate selection of storms to simulate. On top of that, the approach needs to include multiple storms to certify the threshold of T = 2-year is not breached. It is worth noting that this study assumes the design storms last for 2 h, which is an arbitrary threshold to represent the highly convective storms in the region.

Optimizing WRF is not an easy task and can be susceptible to uncertainties. The sources of uncertainty in the hydro-meteorological system include incomplete observations, model initialization, approximate numerical models due to unavoidable simplifications or error in the mathematical representation of the processes, error due to parametrization, and the chaotic nature of the atmosphere, all of which contributed to errors to meteorological, and also to hydrological model results (Palmer 2001; Moges et al. 2021). The largest sources of uncertainty are considered to be due to model initialization and the parametrization schemes, in which all cases determine the processes producing precipitation (Rossa et al. 2011). In this study, the uncertainty due to the model's inadequacy to properly simulate the events is addressed through model sensitivity analysis using a multi-physics ensemble technique; see for detail (Umer et al. 2021). Besides, the latest available Global ERA5 reanalysis dataset is used for model initialization, which is the upgrade of the ERA-Intream at the European Center for Medium-range Weather Forecast (ECMWF) (Hersbach et al. 2020). Due to the ERA5 reliance on the land surface model and assimilation configuration consistent with those used for operational NWP with coupled land–atmosphere simulation, the product is robust and widely used for practical application. Besides, the soil water information used in WRF is updated based on the soil information derived from SoilGrids (Umer et al. 2019), while the urban model information, the position and extent of the city and urban parameters were updated following (Oliveros et al. 2019). Besides all these efforts done, there still can be associated uncertainties that one could not avoid mainly because of lack of observation and the chaotic atmosphere dynamics, all of which lead to uncertain model results (Rodríguez-Rincón et al. 2015).

Even though the overall model results over the catchment are good compared to the observations, WRF does not produce pixel-precise results, i.e., the spatial patterns of rainfall do not coincide with ground-based measurements. This variability of spatial patterns is a common problem with many mesoscale NWP models configured at high spatial and temporal resolution. The patterns are a result of complex atmospheric physics of the entire lower atmosphere, and the interaction with the earth's surface can still be improved (Ryu et al. 2016; Paul et al. 2018). This imprecision is not immediately a problem for flood hazard analysis, as a hazard is not based on a single real event but should represent a potential situation: for a given storm of a known size and probability of occurrence, the potential maximum effect (i.e., water level and extent) is simulated. Therefore, in our case, that flood hazard-triggered event can be derived from anywhere as long as it is representative of the weather patterns of Kampala. Practically by selecting the grid cells in the inner domain area, they are assumed to be representative for the region, which is only a practical choice. More research would be needed to determine which area can be considered representative for an area. Here, we used threshold criteria to select the potential grid cells and then applied a quantile expression to select three representative gridcell events per event. The choice of quantiles description is a systematic strategy to make a fair decision on using the potential grid cells for flood hazard modeling. However, a change in the threshold criteria could result in different design storms; in particular, the lower quantile and middle quantiles affected a lot with a deviation in minimum criteria.

The WRF design storms were compared with the results of IDF-AB design storms in terms of cumulative rainfall, peak intensity, and time dynamics. Although the events' structure and time dynamics are almost identical, the cumulative rainfall and peak intensity of WRF design storms are overestimated or underestimated compared to IDF-AB storms because of the following two conditions. Firstly, the known condition related to defining the storm when using the IDF-AB design storms. For a given return period, IDF-AB considers a worst case scenario storm which have never been observed, but they are statistically derived extremes ignoring actual rainfall patterns and properties found in the rainfall registers (Di Baldassarre et al. 2006). Deriving these extremes is uncertain, particularly when based on limited historical data and under changing climate conditions (Hall 2014). More importantly, IDF-AB design storm estimation does not take into account the spatial variability of the rainfall events as it is constructed based on a station located in the city center or airport that might not reflect the rainfall properties at different corners of the city. In contrast, WRF designs storms, being developed based on real rainfall events, they are able to consider the spatial distribution of the events over the city. The other condition for the discrepancy of the rainfall properties between the two designs storms can be due to the inherent uncertainty of WRF simulated gridcell rainfall events, as discussed above, which is unavoidable but can be managed accordingly. In particular, the extremely high rainfall amount and peak intensity for WRF3U might be attributed to this uncertainty.

In the second part of this study, the resulting design storms are used as input to the openLISEM model. An important aspect of this study is that we evaluate only the applicability of the constructed design storms for flood hazard modeling by using the established and calibrated flood model. In most hydrological analyses that require design rainfall storms to evaluate the effect of extreme rainfall events on flooding in urban areas, large errors can occur in estimating these rainfall characteristics. These errors can be considered as the cascade of uncertainties from data used to construct design rainfall to flood model results (Wu et al. 2011). In this study, the results of large flood characteristics values (large peak discharge and deep food depth) in the case of WRF3U when benchmarked with the model results from IDF-AB design storms might be attributed to this uncertainty.

It has to be acknowledged that the flood hydrology model will introduce another uncertainty to the results, which can be of either model structure uncertainty or uncertainties due to the hydrological model parameters (Moges et al. 2020). In order to reduce their influence, the flood model is set up with the best available data, particularly soil water information, digital elevation model, and roughness values (Umer et al. 2019). Moreover, the openLISEM model set up the following recommendations of published papers for the best possible representation of the case study, specifically regarding the selected spatial resolution and input data as suggested by Chogyal (2013); Sliuzas et al. (2013) as well as the consideration of the urbanization impact (Perez Molina 2019). However, due to the complexity of the catchment processes involved as well as the scarcity of measurements at appropriate measures, the results can be susceptible to uncertainty. Therefore, the end-user must consider this reality when using the output of this result for practical applications.

The method proposed herein, as other simple design storm approaches, has limitations. Firstly, the method is only applicable in the geographical locations with local rainfall information or regional IDF curves. As the regional IDF curve is almost easily available, it can be used as an alternative data source in the absence of local rainfall information. Secondly, the constructed design storms represent the real events as simulated by the WRF model. The derived WRF design storms do not represent multiple events; hence, not applicable for the continuous-time hydrological modeling system, for instance, for actual flood modeling or the early warning system. Despite that, the proposed approach is simple, solid, and expected applicable in other locations with data-scarcity issues. The mesoscale NWP model, WRF, used to simulate high-resolution rainfall in space and time, is a flexible model with a variety of input data, particularly in limited resources. And also, its ability to leverage model advancements from a global research community makes it applicable at any location (Dudhia 2014). Purely as a method to derive design storms using WRF rainfall product, the main challenge here is to properly do multi-physics parameterization schemes, which is a large task and is also area-dependent. However, many meteorological services in countries use the WRF model or other weather models for weather forecasting, so good knowledge on the local parametrization of a weather model may be locally available. Moreover, some other uncertainty in the model, such as model initialization, could also be reduced by using the data assimilation strategy, which is also freely available, and the strategy to use it is already available, for instance (Routray et al. 2010; Yucel and Onen 2014).

6 Conclusions

The main aim of this study was to present a new methodology to translate WRF simulated high-resolution convective rainfall events into a design storm form and evaluate its performance against the existing alternating-block method design storms obtained from the pre-established IDF curves. The differences between the WRF and IDF-AB design storms are evaluated from the point of view of flood hazard modeling and then discussed the strengths and weaknesses of our proposed method. In order to do this, we developed WRF design storms based on the spatial distribution of high-intensity rainfall events simulated at high spatial and temporal resolutions. The potential gridcell events were selected and translated to the WRF design storm form using a quantile expression of the cumulative rainfall distribution. Consequently, three different WRF design storms per event were constructed: lower (WRFL), median (WRFM), and upper quantiles (WRFU). The results are compared with IDF-AB design storms of 2- and 10-year return periods (i.e., AB2yr and AB10yr) to evaluate differences from a flood hazard assessment point of view. We found that the developed WRF design storms performed well compared to the alternating-block design storms, particularly the results between WRFL vs. AB2yr and WRFU vs.AB10yr. WRFLs produce hydrographs similar to that of AB2yr, with their peaks quickly attenuated by the existing structure and the wetlands. The WRFUs also produce hydrograph similar to AB10yr, except for WRF3U, which has a slightly higher peak hydrograph (+ 4%) than the existing channel capacity. In order to evaluate the appropriateness of the WRF design storms for flood hazard assessment, we compared the maximum flood depth at every grid-cells in terms of frequency distribution. We found that for both WRFLs vs. AB2yr and WRFUs vs. AB10yr, the number of the grid-cells and intensity of the flood depths are higher when using WRF design storms. Moreover, the use of WRF3U for flood hazard modeling leads to more maximum flood depths of over 2 m per grid-cells compared to AB10yr.

Nevertheless, the overall definition of the WRF design storms is greatly affected by the selection criteria, which would subsequently affect the flood dynamics in the catchment. Notably, the chosen threshold can affect the lower and median quantiles even though the interest tends to focus on the extreme event represented by the upper quantile from the flood hazard point of view. In our case study, the flood in Kampala is considered hazardous with the design storm of a 2-year return period; as such, we decided on our threshold based on the existing local information to showcase the method. Besides, by using the quantile descriptions, the results would not be overly sensitive to the criteria. Eventually, the threshold could come from the regional information, not necessarily the accurate local information is needed.

The result suggests that the WRF design storm can be obtained from the grid-cell rainfall events, which are defined as the representative rainfall pattern over the catchment. This design storm can be considered as an added value for flood hazard assessment as they are closer to real systems that are causing rainfall. However, more research is needed on which area can be considered as a representative area in the catchment. The main weakness in using the NWP model output for flood hazard modeling in the data-scarce area is having a validated WRF rainfall product, as limited observed data can lead to modeling and model result uncertainties. Even with these uncertainties, the construction of design storms is considered solid and robust, as the three events gave rather similar design storms. More importantly, this quantile description allows for more diverse design storms, doing justice to the atmospheric systems causing large-scale or convective rainfall over the area. However, as many areas have validated numerical weather prediction models or have sufficient observed data to validate the model, this approach has the potential to be applied in many more regions to support integrated flood management. The methodology presented in this study can provide a baseline for real event design storm construction based on low-cost numerical weather prediction rainfall products. The result has an added value for flood risk applications in the data-scarce areas, which is the core of integrated flood management. This new approach would address the known uncertainties in flood risk analysis, which consists of hazard analysis as well as vulnerability and exposure analysis.