1 Introduction

Probabilistic seismic hazard analysis (PSHA) has become a standard practice for describing the seismic hazard of a site and for providing ground motion input for seismic design; results are in the form of exceedance probability of annual ground motion. PSHA provides a basis for minimizing losses caused by future ground motions. The Cornell–McGuire method, the most commonly used method in PSHA, was proposed by Cornell (1968) and later developed by McGuire (1976) as a computer program.

PSHA has made great progress since the development of the Cornell–McGuire method but remains controversial in some aspects, such as the irrationality of PSHA calculation at a very low exceedance probability, leading to ground motion that does not fit the actual physical meaning. For critical facilities, the seismic hazard must often be calculated as annual exceedance probabilities of 10–6 (for nuclear power plants) to 10–9 (for nuclear waste repositories) (Baker et al. 2013). At these extremely low exceedance probabilities, the ground-motion values calculated by PSHA are often unrealistically high, as with the PSHA results for a nuclear waste disposal site in the Yucca Mountains, USA. This project was implemented in accordance with United States SSHAC-97 guidelines (Budnitz et al. 1997), and the results were so high that peak ground acceleration (PGA) and peak ground velocity with an annual probability of exceedance of 10–8 reached 11 g and 13 m/s, respectively (Stepp et al. 2001). These results were intensely debated among experts, and a series of studies concluded that the PSHA results of the project were excessively high (Andrews et al. 2007; Stamatakos 2017).

The primary reason for this phenomenon is that the lognormal function used in PSHA calculation to characterize the conditional probability distribution of a given earthquake extrapolates the lognormal distribution to high multiples of standard deviation unrelated to realistic ground motions. Probabilistic seismic hazard results for extremely low exceedance probabilities are primarily controlled by the shape of the tail of the ground-motion distribution (Anderson and Brune 1999; Wang 2011). The lognormal distribution has no upper bound on the right side, creating a PHSA hazard curve without an upper bound at a low exceedance probability.

A truncated lognormal distribution is commonly used to avoid overestimating low-probability hazards. However, selecting a truncation level is difficult and relatively subjective, because the method lacks clear physical meaning (Strasser et al. 2008).

Studies have focused on the distribution of the residuals of ground motion to solve this problem. Huyse et al. (2010) analyzed data from the Pacific Earthquake Engineering Research-Next Generation Attenuation of Ground Motions database and PGA residuals using Abrahamson and Silva's NGA ground-motion relations. They concluded that the tail shape of the PGA residuals is more likely to perform as a generalized Pareto distribution (GPD) than as a lognormal distribution. Similarly, Pavlenko (2015) used the Kolmogorov–Smirnov (KS) test and the Akaike information criteria (AIC) to test the generalized extreme value distribution (GEVD) and lognormal distribution both fitted by maximum likelihood (ML) method for PGA residuals. The results showed that GEVD and GPD as the middle and upper tail residual distributions produced higher accuracy than the lognormal distribution. Additionally, aleatory variability in ground-motion prediction of PGA can be characterized by a GEVD (Dupuis and Flemming 2006; Raschke 2013; Pavlenko 2017; Borzoo et al. 2020).

However, in the above-mentioned research on the residual distribution of ground motion, the variation with magnitude of the distribution of ground-motion residuals has not attracted enough attention. Heteroscedasticity may cause a difference in residual distribution, and ground-motion scatter decreases as magnitude increases (Abrahamson and Silva 1997, 2008; Sadigh et al. 1997; Campbell and Bozorgnia 2004; Bommer et al. 2007).

Therefore, we considered the heteroscedasticity of the magnitude when fitting the ground-motion residuals in our study. Referring to the grouping criteria of ground-motion residuals in the attenuation relationship established by Campbell and Bozorgnia (2014) (CB14), we divided the residuals calculated by CB14 into three sets with different magnitudes. The peak-over-threshold (POT) method was used to fit the GPD (Embrechts and Mikosch 1997). The results were compared with the GPD fitted by the residuals and the lognormal distribution. Finally, we established a model that consisted of a lognormal distribution (up to the threshold of the ground-motion residual) and the GPD and discussed its influence on the PSHA results.

2 Methods

An overview of the extreme distribution must be provided to understand the scope of our method and the ability to interpret the results. Brief definitions of the GPD and the POT method are reviewed below.

\(X_{1} ,X_{2} , \ldots ,X_{n}\) is a sequence of independent and identically distributed non-degenerate random variables with distribution \(F\left( x \right). M_{n} = \max \left( {X_{1} ,X_{2} , \ldots ,X_{n} } \right)\) denotes the maximum value. If series \({ }\left\{ {a_{n} > 0,b_{n} \in R} \right\}\), and a non-degenerate distribution function \(H\left( x \right)\) that satisfies the following formula exist:

$$\begin{array}{*{20}c} {\mathop {\lim }\limits_{n \to \infty } P\left( {\frac{{M_{n} - b_{n} }}{{a_{n} }} \le x} \right) = H\left( x \right)} \\ \end{array}$$
(1)

then \(H\left(x\right)\) is the extreme value distribution, and \(F\left(x\right)\) belongs to the maximum domain of attraction of the extreme value distribution \(H\left(x\right)\); thus, we write \(F\in \mathrm{MDA}(H)\). Fisher and Tippett (1928) obtained three forms of extreme value distribution that can be unified into the GEVD:

$$\begin{array}{*{20}c} {H\left( x \right) = \left\{ {\begin{array}{*{20}c} {\exp \left\{ { - \left( {1 + \xi \frac{{\left( {x - \lambda } \right)}}{\delta }} \right)^{{ - \frac{1}{\xi }}} } \right\}} & {\xi \ne 0} \\ {\exp \left\{ { - \exp \left( { - \frac{x - \lambda }{\delta }} \right)} \right\} } & {\xi = 0} \\ \end{array} } \right.} \\ \end{array}$$
(2)

where \(\lambda\) is the location parameter, \(\delta\) is the scale parameter (\(\delta\) > 0), ξ is the shape parameter, and \(X\) meets \(1 + \xi \frac{x - \lambda }{\delta } \ge 0\). When ξ > 0, \(X\) obeys the Fréchet distribution (extreme value type II). If the tail of F(x) decays like a power function, the distribution is in the Fréchet domain of attraction. These are so-called heavy-tailed distributions. When ξ = 0, \(X\) follows a Gumbel distribution (extreme value type I). Distributions in the Gumbel max domain of attraction include exponential, normal, and lognormal distributions. When ξ < 0, \(X\) corresponds to a Weibull distribution (extreme value type III). Distributions in the Weibull domain of attraction, such as the beta distribution, are light-tailed. Pickands (1975) indicated that for a sufficiently large threshold\(\lambda\), the excess \(X- \lambda\) approximately obeys the GPD. The form of the GPD is:

$$\begin{array}{*{20}c} {G\left( x \right) = \left\{ {\begin{array}{*{20}c} {1 - \left[ {1 + \xi \frac{x - \lambda }{\delta }} \right]_{ + }^{{ - \frac{1}{\xi }}} \xi \ne 0} \\ {1 - \exp \left[ { - \frac{x - \lambda }{\delta }} \right] \xi = 0 } \\ \end{array} } \right.} \\ \end{array}$$
(3)

where \(+\) denotes that the GPD is defined only when the term inside the square brackets is positive. Similar to the GEVD, the GPD is characterized by three parameters: location\((\lambda )\), scale\((\delta )\), and shape (ξ). The value of ξ in the GPD is the same as that of the underlying GEVD. This property is called tail equivalence, as ξ reflects the convergence property of the GPD tail. The larger the ξ, the thicker the tail, and the slower the convergence speed of the tail distribution. In contrast, the thinner the tail, the faster the tail distribution converges. When ξ < 0, the GPD is bounded, and the maximum value of \(X\) is reached when \(X = \lambda - \frac{\delta }{{\upxi }}\).

The GPD appears as a limit distribution with a sufficiently large threshold, which is usually used to fit the empirical cumulative distribution of the tail. The POT method applies GPD fitting to all observed data exceeding a given threshold. The current study focused on fitting the tail of the ground-motion residual distribution. The POT method is suitable for fitting the upper tail distribution of the residuals and is performed for ground-motion residuals exceeding a certain threshold.

A quantile–quantile (Q–Q) plot is generally visually inspected to determine the tail distribution. The Q-Q plot is a graph drawn with the relationship between the quantiles of the sample data distribution and the specified distribution. If the tested data conform to the specified distribution, the points on the Q–Q plot should be arranged approximately in a straight line. For example, the exponential Q–Q plot can be used to identify the tail shape of the distribution. If the data follow an exponential distribution, the points on the graph should be surrounded by a straight line. If the given distribution is light-tailed (ξ < 0), the plot curves up to the right. On the contrary, if the distribution is heavy-tailed (ξ > 0), the plot curves down to the right.

The statistical analysis in this article primarily includes the following steps:

  • Choosing an appropriate threshold for the GPD fit.

  • Estimating the GPD parameters using the ML method.

  • Testing the hypothesis that a residual sample belongs to the GPD with a Q-Q plot.

ML, the most common of many methods used to estimate GPD parameters, provides consistent, efficient, and asymptotically normal estimates (M.Hill 1975). Thus, we used the ML method in our study. The logarithmic likelihood function is monotonically increasing and unbounded with respect to threshold \(\lambda\); thus, the estimator of \(\lambda\) cannot be obtained by the ML method. Therefore, the threshold is given by other methods discussed later. For ξ >  − 0.5, the maximum likelihood regularity conditions are fulfilled, and the maximum likelihood estimates (\(\widehat{\upxi },\widehat{\delta }\)) based on a sample of n excesses are asymptotically normally distributed (Hosking 1987).

3 Data

In this study, the total interevent and intraevent ground-motion residuals were defined as:

$$\begin{array}{*{20}c} {\varepsilon = \ln \left( {PGA_{{{\text{observed}}}} } \right) - \ln \left( {PGA_{{{\text{predicted}}}} } \right)} \\ \end{array}$$
(4)

where \({\text{PGA}}_{{{\text{observed}}}}\) is the actual recorded PGA, and \({\mathrm{PGA}}_{\mathrm{predicted}}\) is the PGA calculated using a specific ground-motion prediction equation (GMPE).

GMPEs—also known as attenuation relations—are functions representing the variation of ground-motion parameters with magnitude, distance, site condition, and other factors. GMPEs are usually empirical and are developed based on multiple ground-motion parameter databases (Boore and Joyner 1982). For a given earthquake, the GMPE allows the prediction of the mean ground motion value for a given site.

In our study, the attenuation relationship established by Campbell and Bozorgnia (2014) (CB14) was chosen to calculate the \({\mathrm{PGA}}_{\mathrm{predicted}}\) and the ground-motion residuals. The CB14 model was developed by the Pacific Earthquake Engineering Research Center (PEER) and referred to as the next-generation attenuation phase 2 (NGA-West2) database, representing the culmination of a four-year multidisciplinary study sponsored by the PEER NGA-West2 Ground Motion Project (Bozorgnia et al. 2014). The NGA-West2 database is a comprehensive and reliable global database, which covers more than 600 earthquakes from 1935–2011, including many recent major earthquakes. Figure 1 shows the distribution of the epicenter locations. The 21,359 earthquake records include the M6.6 Bam Earthquake in 2003, the M7.9 Wenchuan earthquake in 2008, and the M6.3 Christchurch earthquake in 2011 (Ancheta et al. 2014).

Fig. 1
figure 1

Epicenter distribution of 599 events included in the NGA-West 2 database

Full size image

The CB14 data were selected from the NGA-West2 database by the research group of Campbell and Bozorgnia and included 15,521 earthquake records of 322 earthquakes with magnitudes between 3.0 and 7.9 and fault distances between 0 and 500 km. CB14 includes a more detailed hanging wall model than the previous 2008 GMPE (CB08), scaling with hypocentral depth and fault dip, regionally independent geometric attenuation, regionally dependent anelastic attenuation and site conditions, and magnitude-dependent aleatory variability. The prediction formula for the mean value of ground motion of CB14 is as follows (Campbell and Bozorgnia 2014):

$$\begin{array}{*{20}l} {\ln Y = \left\{ {\begin{array}{*{20}c} {\ln {\text{PGA}}\;\quad \quad \quad \quad {\text{PSA}} < {\text{PGA}}\, {\text{and}}\, T < 0.25\,s } \\ {\begin{array}{*{20}c} { } \\ {f_{{{\text{mag}}}} + f_{{{\text{dis}}}} + f_{{{\text{flt}}}} + f_{{{\text{hng}}}} + f_{{{\text{site}}}} + f_{{{\text{sed}}}} + f_{{{\text{hyp}}}} + f_{{{\text{dip}}}} + f_{{{\text{atn}}}} ;\, {\text{otherwise}}} \\ \end{array} } \\ \end{array} } \right.} \\ \end{array}$$
(5)

where \(\ln Y\) is the natural logarithm of the ground motion of interest, and the \(f\)-terms represent the scaling of ground motion with respect to earthquake magnitude, geometric attenuation, style of faulting, hanging wall shallow site response, basin response, hypocentral depth, fault dip, and anelastic attenuation. The specific formulas of these terms are detailed in Campbell and Bozorgnia (2014).

4 Result and analysis

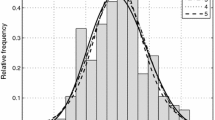
After screening the NGA-West2 database according to CB14, we excluded 28 records without actual PGA observations and selected the remaining 15,493 records for analysis. We used Eq. (4) to calculate the PGA residuals. Figure 2a shows that the residuals roughly conformed to a normal distribution, with an average mean of 0. However, Fig. 2b reveals that the lognormal distribution on the right tail did not fit the residuals well with increasing deviation. In Fig. 2c of the exponential (Q-Q) plot, the data curves upward compared with the reference line; thus, the residual data should follow a light-tailed distribution. Huyse et al. (2010) drew a similar conclusion using the ground-motion relations of Abrahamson and Silva (2008). Therefore, we used the POT method to perform GPD fitting on the right tail of the residual distribution.

Fig. 2
figure 2

Normal distribution of 15,493 PGA residuals calculated using the CB14 a overall distribution b tail distribution c Exponential Q–Q plot

Full size image

When fitting the excess with the GPD, the primary problem is the selection of the threshold λ. If λ is too large, few excesses and insufficient data lead to excessively large estimator variance; if λ is too small, large deviation between the excess distribution and the GPD leads to a biased estimation. Therefore, a compromise between bias and variance is needed for λ selection. We adopted a straightforward graphic method to determine λ based on the average excess function \(E(PGA - \lambda |PGA > \lambda )\) (Stuart 2001), where \(E\left( \cdot \right)\) denotes expectation. If a random variable follows the GPD, the average excess function is approximately a linear function of λ. Figure 3 shows the sample average excess relative to the threshold. We suggest a value of 1.5 for the threshold of the right tail with a coefficient of determination R2 = 0.91. This threshold is located at the beginning of a portion of the mean excess plot that is roughly linear; the remaining 494 points in the tail account for approximately 3% of the total. We also consider 2.0 and 2.2 as possible thresholds.

Fig. 3
figure 3

Mean excess function for all residuals

Full size image

The excess corresponding to an appropriate threshold follows the GPD distribution; thus, the estimator of the shape parameter and the modified scale parameter \(\delta^{*} = \delta \cdot \xi - \lambda\) should remain unchanged (McNeil 1997; Brabson and Palutikof 2000; Clauset et al. 2009). Because there is no clear procedure for the highly accurate threshold selection, δ* must remain robust when faced with variations in the errors during selection (Rodríguez 2017). To further examine the selected threshold value, we used the ML method with the ismev package in R (http:\\www.r-project.org) to estimate the shape and scale parameters under different thresholds (Fig. 4). The shape and modified scale parameters fluctuate higher than approximately 1.5; the 95% confidence interval gradually increases, indicating the large uncertainty of the estimated parameter. The GPD parameters estimated by the ML method and other tail statistics associated with each threshold level are summarized in Table 1. As the threshold increases, the 95% confidence interval of the estimated shape parameters progressively increases. Thus, for the robustness of the estimated shape parameter, a threshold of 1.5 may be an optimal choice for this GPD fit.

Fig. 4
figure 4

Parameter estimation of the GPD against the threshold

Full size image
Table 1 Generalized Pareto distribution fitting results
Full size table

Additionally, although the 95% confidence interval of the estimated shape parameter increases as the threshold increases, the estimated shape parameter remains negative (Fig. 4). This further demonstrates that the sample data conform to the GPD with a right upper bound.

Figure 5 shows a comparison of the complementary cumulative distribution function (CCDF) of the empirical distribution of the residuals, the lognormal distribution, and the GPD fitted by all 15,493 residuals. The GPD fits the data points well in the tail and describes the finite upper bound trend. The lognormal distribution overestimates the quantile of most data points, and the deviation between the lognormal distribution and the actual data points is evident toward the right end. Therefore, the GPD describes the shape of the residuals in the tail better than the lognormal distribution.

Fig. 5
figure 5

Comparison of complementary CDF between the GPD and the lognormal distribution

Full size image

Figure 6 shows the Q–Q plot of the GPD fitting results. As can be seen from Fig. 6 that data points larger than the 1.5 threshold surround the reference line, indicating that the GPD fit to the data points in the tail is appropriate.

Fig. 6
figure 6

Quantile–quantile plot of the GPD fitted by all residuals

Full size image

5 GPD fitting for different magnitudes

Boore et al. (1993) examined the magnitude dependence of the residuals of their equations for the PGA. The PGA results were consistent with the findings of Youngs et al. (1995): the data exhibited decreased scatter and increasing magnitude. Heteroscedasticity caused by magnitude is now considered in many GMPEs, such as CB14. Therefore, in this section, we address the impact of heteroscedasticity on the residual distribution and GPD fitting.

Figure 7 shows the residuals calculated in this study and the complementary function of the empirical distribution function at the tail of the residuals with two different magnitude ranges. For smaller magnitudes (M ≤ 4.5), the residual distribution is closer to the overall distribution; however, residuals with larger magnitudes (M > 5.5) are significantly different from the overall residual distribution. The maximums of the residuals with larger and smaller magnitudes are approximately 2.4 and 3, respectively. Toward the tail, the standard deviation of the residuals with large magnitudes is smaller than that of residuals with smaller magnitudes and that of all the residuals (the slope in the plot that approximates the standard deviation). The aforementioned results indicate large differences in the distribution of ground-motion residuals with different magnitude ranges toward the tail. Therefore, if the GPD fitting parameters of the overall residuals are used for PSHA calculation, the hazard of a larger magnitude will be overestimated, especially at a low exceedance probability.

Fig. 7
figure 7

Complementary CDF of empirical distribution of residuals with different magnitudes

Full size image

Therefore, GPD fitting was conducted for residuals with different magnitudes to obtain a more accurate ground-motion model. We divided the residuals into three sets by magnitude in accordance with the group of standard deviations in CB14: M ≤ 4.5, 4.5 < M ≤ 5.5, and M > 5.5. For these three sets of data, the POT method was applied to perform GPD fitting on the tail. We adopted the same method of threshold selection as in Sect. 4 through the analysis of the average excess function and the estimated GPD parameters against the thresholds. Additionally, the maximum likelihood method was used to estimate the parameters. The fitting results are listed in Table 2. The residuals of the three magnitudes follow the GPD with different parameters. The shape parameters are all negative, indicating that the distributions have a right upper limit. As the magnitude increases, the shape parameters gradually decrease; thus, the residuals with large magnitudes converge to the upper limit faster and have a smaller upper limit on the right side.

Table 2 Generalized Pareto distribution fitting results for different magnitudes
Full size table

Figure 8a, b, and c shows a comparison of the GPD fitting curves with three magnitude ranges, the lognormal distribution (fitted to grouped data points), and the overall GPD (fitted to all data points). 1) For residuals divided into the three magnitude ranges, the lognormal distribution overestimates the data point quantiles, especially in a fraction of the right tail. The lognormal distribution is approximately a straight line in Fig. 8a, b, and c, whereas the actual data points tend to gradually converge as they approach the tail. 2) The difference between the actual data points and the GPD fitted by the overall residuals is significant. The fit curve of the overall GPD for the moderate-magnitude group (4.5 < M ≤ 5.5) passes through most of the points, but the deviation between the curve and data points is more significant closer to the upper bound; further, the fitting curve underestimates the quantile of the residuals of the small-magnitude group (M ≤ 4.5). In contrast, the fitting curve overestimates the quantile of residuals of the large-magnitude group (M > 5.5) in the tail. 3) The GPD curves obtained by grouped residuals fit the data points well, with a converging trend. In the moderate-magnitude group, the last data point is far from the fitting curve (an outlier after analysis) and was excluded during fitting.

Fig. 8
figure 8

Comparison of the GPD fitted to residuals with different magnitudes and the GPD fitted to all residuals and the lognormal distribution a M ≤ 4.5, b 4.5 < M ≤ 5.5, and c M > 5.5

Full size image

The Q–Q plot was used to test the goodness of fit with the R-square of the linear regression of points in Fig. 9a–c for the GPD fitted by different magnitudes. The above-mentioned comparison showed that the GPD fitted to three different ranges of magnitude is preferable for performing the tail distribution and largely accounts for the influence of magnitude on the residual distribution. In particular, the distribution of the large-magnitude residuals related to the low exceedance probability is significantly different from the overall residual distribution. Therefore, to obtain a more accurate distribution of the ground motion model, we suggest that the ground-motion residuals should be fitted by the GPD for different magnitudes.

Fig. 9
figure 9

Quantile–quantile plot of the GPD fitted by different magnitude residuals a M ≤ 4.5, b 4.5 < M ≤ 5.5, and c M > 5.5

Full size image

6 Implication for PSHA

The aleatory variability in the GMPE is an important characteristic of PSHA, which differs from deterministic seismic hazard analysis. Bommer and Abrahamson (2006) conducted an extensive review and emphasized the importance of incorporating the aleatory variability of ground motions into PSHA. They concluded that the aleatory uncertainty was ignored in early studies, explaining why the hazards were much lower than those of probabilistic hazard studies conducted in recent years. Therefore, the aleatory uncertainty of ground motion in PSHA must be considered.

However, using a lognormal distribution to characterize ground motion is not optimal, because the lognormal distribution is an unbounded function with a nonzero probability for large or physically impossible ground motions. This problem is commonly solved with the use of a truncated lognormal distribution to model the ground-motion scatter in PSHA. Nevertheless, the truncation operation poses problems. If the lognormal distribution is artificially truncated (e.g., three times the standard deviation), the hazard curve will distort actual ground-motion records. Moreover, the selection of the truncation multiple may be arbitrary. This section demonstrates that the combination of the lognormal distribution and the GPD should be performed to characterize ground-motion scatter in PSHA calculations.

To illustrate the effect of using GPD instead of the lognormal distribution to represent the tail of the residual, this section intends to use the following models to characterize scatter for PSHA calculations:

  1. 1.

    Lognormal distribution.

  2. 2.

    Truncated lognormal distribution.

  3. 3.

    Composite models (lognormal distribution and GPD distribution).

To better understand the following content, we briefly introduce the basic principles of PSHA calculation. The first is the probability density function (PDF) of the PGA, which follows a lognormal distribution and can be written as:

$$\begin{array}{*{20}c} {f_{{\mu_{Y} ,\sigma_{Y} }} \left( {{\text{PGA}}} \right) = \frac{1}{{\left( {{\text{PGA}}} \right)\sigma_{Y} \sqrt {2\pi } }}e^{{ - \frac{{(\ln \left( {{\text{PGA}}} \right) - \mu_{Y} )^{2} }}{{2\sigma_{Y}^{2} }}}} ,{\text{PGA}} > 0} \\ \end{array}$$
(6)

where Y = \({\text{ln}}\left( {{\text{PGA}}} \right)\) is a normal random variable with a mean value \(\mu_{Y}\) and standard deviation \(\sigma_{Y}\). The mean and standard deviation were obtained from a specified earthquake prediction model (e.g., CB14). For a given earthquake with magnitude M, the probability of producing ground motion exceeding \(a_{0}\) at a distance R is:

$$\begin{array}{*{20}c} {P\left( {Y \ge \ln \left( {a_{0} } \right)m,r} \right) = \frac{1}{{\sqrt {2\pi } \sigma_{Y} }}\mathop \smallint \limits_{{a_{0} }}^{\infty } e^{{ - \frac{{(Y - \mu_{Y} )^{2} }}{{2\sigma_{Y}^{2} }}}} dy} \\ \end{array}$$
(7)

which can be simplified in the form of a standard normal distribution to:

$$P(Y \ge \ln (a_{0} )m,r) = 1 - \Phi (Z)$$
(8)

where \(z = \frac{{{\text{ln}}\left( {a_{0} } \right) - {\upmu }_{Y} }}{{{\upsigma }_{Y} }}\) is a standard normal random variable, and \({\Phi }\left( Z \right)\) is the CDF of the standard normal distribution.

Suppose N potential sources contribute to a given site, each with magnitude \(M_{i}\), distance \(R_{i}\), and annual rate \({ }v_{i}\); \(M_{i}\) and \(R_{i}\) are random variables, each having a PDF of \(f_{{M_{i} }} \left( m \right)\) and \(f_{{R_{i} }} \left( m \right)\). Then, the annual rate at which the ground motion of the site exceeds \(a_{0}\) can be expressed as:

$$\begin{array}{*{20}c} {v\left[ {Y \ge \ln \left( {a_{0} } \right)} \right] = \mathop \sum \limits_{i = 1}^{N} v_{i} \iint {P\left( {Y \ge \ln (a_{0} )m,r} \right)f_{{M_{i} }} \left( m \right)f_{{R_{i} }} \left( r \right)dmdr}} \\ \end{array}$$
(9)

The aleatory uncertainty of the ground motion is reflected in the conditional probability distribution of \(P\left( {Y \ge \ln \left( {a_{0} } \right)|m,r} \right)\). Small annual exceedance rate values (\(v\left[ {Y \ge \ln \left( {a_{0} } \right)} \right] \ll 1\)) (Eq. (9)) can be approximated as annual exceedance probability (Pavlenko 2015).

Next, we introduced a truncated lognormal distribution. If a lognormal distribution is truncated at PGA = \({a}_{T}\), its PDF needs to be standardized to ensure that the integral of the PDF is 1 when the PGA reaches the cutoff value. Then, the probability that ground motion annually exceeds \(a_{0}\) can be expressed as:

$$\begin{array}{*{20}l} {P\left( {Y \ge \ln \left( {a_{0} } \right)m,r} \right) = \left\{ {\begin{array}{*{20}c} {1 - \frac{\Phi \left( z \right)}{{\Phi \left( {z_{T} } \right)}},} & {Y \le a_{T} } \\ {0,} & {Y > a_{T} } \\ \end{array} } \right.} \\ \end{array}$$
(10)

where \(z_{T} = \frac{{{\text{ln}}\left( {a_{T} } \right) - {\upmu }_{Y} }}{{{\upsigma }_{Y} }}\) are the selected truncation multiples of the standard deviation.

Finally, we used a composite model that combines the lognormal distribution and the GPD to describe the PGA. We established the overall GPD composite model (fitted by the overall residuals) and the grouped GPD composite model (fitted by residuals of different magnitudes combined with the lognormal distribution). The integration of hazards before \({a}_{\lambda }\) used a lognormal distribution, and the tail that exceeded the threshold \({a}_{\lambda }\) used the GPD for integration. The overall GPD composite model to calculate the probability that the ground motion of the site annually exceeds \(a_{0}\) can be expressed as:

$$\begin{array}{*{20}c} {P\left( {Y \ge \ln \left( {a_{0} } \right)m,r} \right) = \left\{ {\begin{array}{*{20}c} {1 - \left( {1 - p} \right)\frac{\Phi \left( z \right)}{{\Phi \left( {z_{\lambda } } \right)}},} & {\ln \left( {{\text{PGA}}} \right) \le \mu_{Y} + \lambda } \\ {p\left( {1 - G\left( {{\text{PGA}}} \right)} \right),} & {\ln \left( {{\text{PGA}}} \right) > \mu_{Y} + \lambda } \\ \end{array} } \right.} \\ \end{array}$$
(11)

where \(z_{\lambda } = \frac{{\ln a_{\lambda } - \mu_{\ln Y} }}{{\sigma_{Y} }}\);\({ }a_{\lambda } = \exp \left( {\lambda + \mu_{\ln Y} } \right)\);\(G\left( {{\text{PGA}}} \right) = 1 - \left[ {1 + \delta \frac{{\left( {{\text{ln}}\left( {{\text{PGA}}} \right) - \mu_{{{\text{ln}}\left( {{\text{PGA}}} \right)}} } \right) - \lambda }}{\delta }} \right]^{ - 1/\xi }\); and \(\lambda\), \(\delta\), and \(\xi\) are defined by (3) and given in Table 1. \(p\) is the percentage of excess falling at the tail (Table 1).

The grouping GPD composite model was used to calculate the probability that the ground motion of the site annually exceeds \({a}_{0}\) in one year and is generally consistent with the above-presented formula. Only the GPD parameters (\(\lambda\),\(\delta\),\(\xi\), and \(p\)) are different (taken from Table 2), according to the assigned magnitudes.

For a better illustration, we used a simple hazard calculation example similar to that of H. Field (2006). This example assumes that the site condition is rocky. The sites contain two potential vertical strike-slip fault sources, and the rupture distances are 15 km (\(r_{1} = r_{2} = 15{\text{ km}}\)). The first, on average, produces an earthquake of magnitude 5 every 20 years (\(m_{1} = 5.0,{ }v_{1} = 1/20\)); the second, on average, produces an earthquake of magnitude 7 every 300 years (\(m_{2} = 7.0,{ }v_{2} = 1/300\)). For the given magnitude, distance, and occurrence rates, the rate of ground motion annually exceeding \(a_{0}\) is:

$$\begin{array}{*{20}c} {v\left[ {Y \ge \ln a_{0} } \right] = v_{1} P_{1} \left( {Y_{1} \ge \ln a_{0} m_{1} ,r_{1} } \right) + v_{2} P_{2} \left( {Y_{2} \ge \ln a_{0} m_{2} ,r_{2} } \right)} \\ \end{array}$$
(12)

The PGA is calculated in a given range using Eq. (12) to obtain the hazard curve of the site. Figure 10 shows the calculation results obtained using the four models.

Fig. 10
figure 10

Comparison of PSHA results using several different ground-motion models

Full size image

Figure 10 shows that: (1) the hazard of using the untruncated lognormal model is highest for all PGA values. When the annual probability of exceedance is greater than 10–5, the curves are relatively close to each other; as the exceedance probability decreases, the difference between the curves emerges and gradually increases, revealing that the different ground motion distributions in the tail significantly influence ground motion with low exceedance probability. (2) For annual exceedance probability of less than 10–5, the hazard of the lognormal distribution truncated three times is the lowest. Thus, using the truncated lognormal model for PSHA calculations underestimates the actual hazard. (3) The calculated hazards for the overall and grouped GPD combinations are much smaller than the untruncated lognormal model. Extremely low exceedance probabilities (i.e., 10–6) feature a clear upper bound on the right (2.3 and 1.4 g for the overall GPD composite and grouped GPD models, respectively). (4) The results calculated using the grouped GPD composite and overall GPD models are almost identical for annual exceedance probabilities greater than 10–5. However, as the exceedance probability decreases, the gap between the two widens. The results of the grouped GPD composite model are much lower, primarily because the low exceedance probability of the site is controlled by the large magnitude. According to the above-mentioned fitting results, the tail of the ground-motion distribution established by the grouped GPD at large magnitudes is closer to the actual data points and is much lower than that of the overall GPD.

7 Conclusion

How to reasonably calculate seismic hazard for long return periods has long been controversial. This study conducted research on this issue by using CB14 to calculate the PGA residuals of 15,493 ground motion records from the NGA-West2 database. The POT method was used to fit the overall residuals and the residuals of three ranges of magnitude using the GPD. Overall and grouped GPD composite models were established to characterize the aleatory variability of ground motion. Finally, the PSHA results of the composite models were analyzed. The principal conclusions of this study are as follows:

  1. 1.

    Compared with the lognormal model, the GPD better describes the shape of the residual distribution at the tail; the GPD shape parameters of the fitting results are negative, indicating that the residual distribution has a finite upper bound. The GPD has more physical meaning than the lognormal model without an upper limit.

  2. 2.

    The three tail distributions of residuals with different magnitude ranges are significantly different from that of the overall residuals because of heteroscedasticity. If the overall GPD is applied to characterize the tail ground motion model, the hazard of a larger magnitude event is overestimated. Therefore, fitting all the residuals for different magnitudes to characterize the ground motion scatter is preferable.

  3. 3.

    The PSHA example results show that the curves obtained by several models have considerable differences for exceedance probabilities greater than 10–5. The lognormal model is the largest, followed by the overall GPD composite model and the grouped GPD composite model. Moreover, the hazard curve of the grouped GPD model converges to a smaller upper limit on the right than that of the overall GPD model.

The calculation result of the low exceedance probability in PSHA is primarily controlled by the tail of the ground-motion model. This study suggests that the grouped GPD composite model with different magnitudes should be used instead of the lognormal distribution model to characterize ground motion scatter in PSHA to obtain more accurate seismic hazards, especially at low probabilities. We believe that our findings are relevant for researchers interested in seismic risk analysis. The GPD parameters derived in this study are specific to the ground motion in the NGA-West2 database based on the CB14 attenuation relationship. Thus, our approach should be tested using other ground-motion databases and extensive GMPEs. Additionally, this study focuses on the PGA. However, a similar approach can be applied to the residual distribution of other spectral periods.