Abstract
Urbanization increases regional impervious surface area, which generally reduces hydrologic response time and therefore increases flood risk. The objective of this work is to investigate the sensitivities of urban flooding to urban land growth through simulation of flood flows under different urbanization conditions and during different flooding stages. A sub-watershed in Toronto, Canada, with urban land conversion was selected as a test site for this study. In order to investigate the effects of urbanization on changes in urban flood risk, land use maps from six different years (1966, 1971, 1976, 1981, 1986, and 2000) and of six simulated land use scenarios (0%, 20%, 40%, 60, 80%, and 100% impervious surface area percentages) were input into coupled hydrologic and hydraulic models. The results show that urbanization creates higher surface runoff and river discharge rates and shortened times to achieve the peak runoff and discharge. Areas influenced by flash flood and floodplain increases due to urbanization are related not only to overall impervious surface area percentage but also to the spatial distribution of impervious surface coverage. With similar average impervious surface area percentage, land use with spatial variation may aggravate flash flood conditions more intensely compared to spatially uniform land use distribution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During urbanization, rain water movement and storage at ground surface within a local watershed are significantly altered by the changes in landscape from natural to man-made (Booth 1991). Paved imperviousFootnote 1 materials block water from natural penetration, decreasing the surface infiltration rate. When the precipitation rate is higher than the infiltration maximum rate, excess precipitation will move quickly as overland flow toward a stream channel and contribute to short-term stream response, leading potentially to soil erosion and flooding (Dingman 2015). To assess urbanization impact on flood risk, two common data sources are historical records and flood modeling results. Early studies relate urbanization to the magnitude and frequency of urban flooding through historical field measurements from river gauges and rainfall gauging stations (Anderson 1970; Espey et al. 1966; Hollis 1974; Kinosita and Sonda 1971; Martens 1966; Hollis 1975; Moscrip and Montgomery 1997). More recently, advanced nonstationary flood-frequency models have been used to prove that urbanization has statistically significant effect on the growing magnitude and frequency of floods (Villarini et al. 2009; Prosdocimi et al. 2015). Thanks to the rapid development in computation power, application of complicated flood models has become feasible. Bronstert et al. (2007) used a multi-scale, process-oriented coupling difference model to simulate flood discharge in catchments at different urbanization stages and formulated a series relations between the land use and flood peak discharges under different storm scenarios. In Banasik and Pham’s study, flood hydrographs under two historical land use conditions in different years and one hypothetical land use condition were simulated using a rainfall-runoff model for a small watershed (Banasik and Pham 2010). Also using rainfall-runoff models, flood peak discharges under historical land use conditions in different years were modeled and were found to exhibit large increases in peak discharge due to urbanization (Al-Ghamdi et al. 2012; Zhao et al. 2016). Yin et al. (2015) proposed a novel scenario-based framework where numerical modeling was undertaken to quantify flood risks using three anthropogenic variables (land subsidence, urbanization, and flood defense). Huang, et al. (Huang et al. 2017) simulated inundation area and average depth for land use conditions in three different years in fluvial flood scenarios with a hydraulic model (Yu and Lane 2006a, b). As the main source for land use data, remote sensing images collected by different sensors were evaluated for flood modeling (Verbeiren et al. 2013; Berezowski et al. 2012).
However, the current overland flow models for urban flood simulation tend to simplify the watershed under study by assuming a uniform hydraulic roughness valueFootnote 2 (e.g., Manning’s n-value) (Water 2010; Rossman 2010). Our research aims to address this information gap by providing 2D overland flow patterns at different urbanization stages using distributed land use maps to account for spatially variable hydraulic roughness values. To account for these urbanization stages, land use maps from six different years (1966, 1971, 1976, 1981, 1986, and 2000), hereafter referred to as Case A, and six simulated land use scenarios (0%, 20%, 40%, 60, 80%, and 100% ISA percentages), hereafter referred to as Case B, have been input sequentially into one hydrologic and one hydraulic model. The two software packages, the hydrologic software Hydrologic Engineering Center–Hydrological Model System (HEC-HMS) and the hydraulic software Hydrologic Engineering Center-River Analysis System (HEC-RAS), were coupled in this study. These packages were developed at the US Army Corps of Engineers Hydrologic Engineering Center (HEC) and were chosen for our research because of their high performance and ease of access (Khaghan and Mojaradi 2016; Hashemyan et al. 2015). During an intense rainfall, the limited capacity of urban drainage systems is insufficient to prevent pluvial flooding from taking on the form of a flash flood. As a result, fast convergence of overland flow and man-made drainage system outlet flow to nearby rivers trigger fluvial flooding (Chen et al. 2010; Patra et al. 2016). The combined damage of pluvial and fluvial flooding during an intense rainfall may greatly exceed their individual consequences (Chen et al. 2010; Apel et al. 2016). In most cases, a multi-source urban flooding event is simply classified into one category. Our research involves analyzing both pluvial and fluvial flooding during a precipitation event with two different hydrologic/hydraulic modeling strategies.
2 Study area and data preparation
2.1 Study area
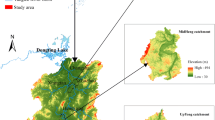
The Don Valley watershed, located in the Greater Toronto Area (GTA) of Ontario, Canada, was used as the study area for software prototyping and application. The lower part of the watershed is in city of Toronto boundary, an area with a long history of damaging urban floods (Armenakis and Nirupama 2014). Although the Toronto municipal government has put great effort into improving its infrastructure from an engineering infrastructure perspective (Kellershohn 2016), flash flooding remains a dangerous and costly hazard that needs to be better understood using good predictive tools. The Don Valley watershed occupies an area of approximately 367 km2. As a highly urbanized and low-lying watershed in Toronto, the Don Valley watershed readily floods even under relatively small rainfall events (Nirupama et al. 2014) (Fig. 1).
2.2 Data
For GTA, rich national and provincial data are available from GeoBaseFootnote 3 (Natural Resources Canada), Scholars GeoPortalFootnote 4 (Ontario Council of University Libraries), and Land Information Ontario.Footnote 5 The City of Toronto also has abundant city data and reports on its website.Footnote 6
2.2.1 Land use/land cover data
Land use data are a key data source to quantify urban growth. Six land use maps from different years (1966, 1971, 1976, 1981, 1986, and 2000) were generated through information assimilation (Zhang et al. 2015). These maps are used by Canada Centre of Mapping and Earth Observation for various urban planning decisions, and the use of them in this study will provide additional and comparable geographic information. These six land use maps were derived from two different data sources. The land use map from year 2000 was derived from Landsat 7 images. The five older land use maps from years 1966, 1971, 1976, 1981, and 1986 were derived from assimilation and integration of Canada Land Use Monitoring Program (CLUMP) maps with the 2000 Landsat map. The assimilation process generated land use maps consistent in both spatial resolution and land use classes. These maps are georeferenced using on a UTM coordinate grid using 35 control points. The spatial resolution of the six land use maps is 30 m. In total, 14 classes are included in the land use maps, i.e., Water, Open urban land, Residential, Commercial/Industrial, Bare rock/Sands, Quarries or Dump, in Construction, Forest/Woods, Farmland, Grassland, Recreational, Wetland, Woody Wetland, and Road. For those land use classes, 30 m resolution is enough and the hydrological features of the same land use can be considered as uniform. Figure 2 shows the six land use maps. The maps illustrate that the GTA has experienced great urban expansion during the 35 years from 1966 to 2000. One of the consequences of urban growth in the GTA is the major conversion of rural land [mainly farmland with good soil for agriculture (Zhang et al. 2010)] to urban land and, consequently significant increase in impervious surface area (ISA). The majority of the urban land is in the form of residential land dominated by detached houses, as well as commercial/industrial land with large sized buildings and paved parking lots. Different urban land uses reflect different levels of imperviousness. During the 35-year period, the GTA has been grown from previously developed urban land of Toronto located in the ‘low land’ on the shore of the Lake Ontario out to upstream areas. In our study area, the Don Valley watershed exhibited an increase in imperviousness from 29 to 49 percent between 1966 and 2000. Most of the development came from the residential land. In addition, the locations of waterbodies are important in urban flood models, as nearby waterbodies are usually the destination of excess surface flows. The hydrographic data used in this research were obtained from the Scholar GeoPortal.
2.2.2 Simulated hyetograph
An important input for the hydrologic model is a hyetograph that represents one historical or theoretical storm event. With an input storm event as the water source, the urban hydrologic model is able to model the surface runoff from the event. This research used a theoretical event derived from the local rainfall intensity duration frequency (IDF) curve. The local IDF curve depicts the characteristics of rainfall in an area through a series of rainfall intensities (mm/hr) over a certain duration (hr) and with a certain return period (year). This research used the IDF curve designed specifically for Toronto, Canada, available from Land Information Ontario, to generate a 24-h 100-year return storm hyetograph.
2.2.3 Digital Elevation Model
The Toronto DEM data used in this research are obtained from Scholar GeoPortal. These provincial tiled data were published in 2006 and are composed of several source elevation data in Ontario. The spatial resolution is 10 m for southern Ontario which includes the Don Valley watershed (Fig. 1). These DEM data were interpolated from the Ontario Base Map that includes both contours and spot heights. Although the DEM of city of Toronto may go through changes during the 35-year time span, we decide to use a single DEM to avoid its impact on urban flooding and keep land use the only changing factors in the modeling.
2.2.4 Soil data
The infiltration rate of soil is affected by subsurface permeability as well as surface intake rates. The United States Department of Agriculture (USDA) divided soil into four hydrologic soil groups (A, B, C, and D) according to their minimum infiltration rate, which is obtained for bare soil after prolonged wetting (Cronshey 1986). Group A has low runoff potential and high infiltration rates. Group B has a moderate infiltration rate. Group C has low infiltration rates. Group D has the lowest infiltration rates and the highest runoff potential. The soil data of the study site used in this research were obtained from Land Information Ontario. Unfortunately, the soil survey did not provide soil type for the urban area. Assumptions had to be made for the large block of urban area based on the soil type of its surrounding rural area. In the Don Valley area, the surrounding soil type is mainly Group C. Thus, we assigned the unknown soil within Don Valley area as Group C. Soil Conservation Service (SCS) curve number (CN) is an empirical parameter in hydrology, developed by the USDA Natural Resources Conservation Service. The CN is used to predict direct runoff or infiltration from rainfall excess. The value of the CN mainly depends on the area’s hydrologic soil group and land use types. CN has a range from 30 to 100, lower numbers indicate low runoff potential, while larger numbers are for increasing runoff potential. The USDA provides tables of CN according to hydrologic soil group and land use (Cronshey 1986).
3 Methods
A coupled hydrologic and hydraulic simulation has been used in this work, where HEC-HMS describes runoff generation and HEC-RAS describes runoff routing. The HEC-HMS model considers the complete hydrologic cycle and calculates the water gain, loss, and transfer using hydrologic balance equations. The HEC-RAS model takes the water excess results from the hydrologic model as boundary conditions and simulates the 2D water movement in the overbank areas. Figure 3 shows the entire workflow of this study. The left side illustrates data collection and pre-processing. The right side outlines HEC-HMS and HEC-RAS modeling using the input data. At the beginning, a simulated storm is derived from an intensity–duration–frequency (IDF) curve and input into HEC-HMS model. This input storm initiates the water movement. Depending on the DEM, soil type, and land use type of the land surface, part of rainfall goes to the groundwater water cycle (blue arrows), traveling slowly in the hydrologic system and do not contribute to flooding. The rest of the rainfall, i.e., rainfall excess, stays on land surface and generates flash flooding or creates temporary ponds, which is the first process studied in this paper. This part applies a rainfall reduction procedure by inputting the rainfall excess derived from the HEC-HMS model as a spatially variable rainfall for each individual sub-basin in the HEC-RAS model. Then, as rapid runoff of rainfall quickly goes to the river system, overbank flow from the river will be expected, which is the second process studied in this paper. This part uses the river hydrograph results from the HEC-HMS model to initiate flood model along rivers. One thing needs to be noticed is that the calculation unit in HEC-HMS is sub-watershed and the calculation unit in HEC-RAS is hydraulic cell. The sizes of both sub-watershed and hydraulic cell are manually set by users. The size of sub-watershed depends on the complexity of terrain. A complex terrain may require a bigger group of small sub-watersheds to be delineated, and a uniform terrain may be well delineated with a smaller group of large sub-watersheds. In this study, we used 10 km2 as the target sub-watersheds size considering the terrain condition in Don Valley. On the other hand, the smaller the size of hydraulic cell, in more detail the water flow will be calculated. However, this step requires a lot of computation power and is very time-consuming. Considering the resolution of DEM and land use, as well as our computation power, we used 20-m hydraulic cell in this study. Furthermore, HEC-HMS and HEC-RAS are not specifically designed for urban area. Thus, the man-made understory drainage networks and building footprints cannot be directly included in the model. Although there are ways to consider the drainage networks and building footprints in the model (e.g., change the infiltration rate along drainage lines, and assign high surface roughness value in building areas), it is beyond the scope of this research. Thus, we do not take these two urban features into consideration in this study. Since the focus of this study is to find the relation between land use and urban flooding, this simplified model will still provide instructive results.
4 Results
4.1 Results from the HEC-HMS
4.1.1 Sub-basin surface runoff
For the flash flood simulation, the watershed rainfall excess relative to surface runoff is the key result from the HEC-HMS model used in the HEC-RAS model. The infiltration rate in a given sub-basin was selected based on the land use type and soil type. Depending on the infiltration rate, the surface runoff amount and the time when the peak discharge occurs were calculated for each sub-basin. In total, 39 sub-basins were delineated based on the DEM in the study area and the rainfall excess and surface runoff values were calculated for each of the sub-basins based on their individual infiltration rates. Four sub-basins (Fig. 4-1) were selected as examples to show how urbanization affects the surface runoff. Two of the example sub-basins, 570 and 480, are located at the upstream end of the drainage basin, and other two sub-basins, 720 and 650, are located at the downstream end of the drainage basin. The surface runoff rate is negatively closely correlated to the size of the sub-basin. The example sub-basins 480, 570, 650, and 720 cover areas of 6.8 km2, 15.5 km2, 36.5 km2, and 8.4 km2, respectively.
Figure 4 shows surface runoff curves from Case A and B experiments for the four example sub-basins. The colored curves are from Case A, and the gray curves are from Case B. For all four sub-basins, the surface runoff patterns for Case B are similar, where the increases in ISA percentages create higher surface runoff rates and shorten the time that takes to achieve peak runoff. In regard to Case A, differences exist among the four sub-basins due to their different urbanization levels. Sub-basin 570 experiences the greatest increase (47.7%) in ISA from the year 1966 to 2000. As a result, the surface runoff rates in sub-basin 570 have a noticeable increase with time and peak times occur earlier from 1966 to 2000. Sub-basins 480 and 650 experience much smaller increases (8.1% and 11.5%, respectively) in ISA from 1966 to 2000. The surface runoff rates in sub-basins 480 and 650 exhibit detectable but limited increases with time. Sub-basin 720 is a highly urbanized area from the year of 1966 and has no detectable change in ISA percentage through from 1966 to 2000. Its surface runoff rates remain constant. The use of spatially detailed land use information in Case A indicates that even in scenarios of small averaged ISA percentage, higher surface runoff rates are predicted than is the case for the Case B scenarios of the same averaged ISA value. For example, the surface runoff rates of sub-basin 570 in year 2000 with a 52.6% ISA percentage are higher than surface runoff rates derived from the simulated data with a 60% ISA percentage.
4.1.2 River hydrograph
The river hydrograph, i.e., the rate of flow at a specific time on a specific section in a river, is a key output from HEC-HMS simulation. The river hydrograph rate was used in HEC-RAS modeling. Runoff in each sub-basin may reach the river to increase the hydrograph from upstream to downstream. Only locations where hydrograph changes due to additional sources of inflow are used as input unsteady flow data in the HEC-RAS model. Six example locations (Fig. 4-2) along the river reaches were selected to show how urbanization influences their hydrograph. The colored curves are from Case A, and the gray curves are from Case B. The hydrograph patterns in Case A indicate that urbanization leads to an increase in peak discharge and shortening of the time to reach peak flow during an event. In the Don Valley watershed, obvious increases in ISA percentage happened between the years 1966 to 1971 (6.2%) and the years 1986 to 2000 (9.3%). In the period between 1971 and 1986, only a 3% increase was found in ISA. For the four upstream river locations (from 1 to 4), the later ISA increase from the years 1986 to 2000 produced greater increase in the river flow rate than the previous ISA increase from the years 1966 to 1971. In contrast, for the two downstream river locations 5 and 6, the previous jump in ISA percentage produced a greater increase in the river flow rate than the later one. This phenomenon may relate to the mechanism of how upstream newly developed urban land exerts pressure on the already-urbanized downstream area. Case B provides further evidence that increased ISA percentages lead to river hydrographs with higher peaks. At locations 1, 3, 5, and 6, Case A data with a smaller average ISA percentage resulted in higher river hydrograph rate, compared to the Case B data with higher averaged ISA percentage but resulted in lower river hydrograph rate. This suggests that the spatial variation in urban land use distribution is a key parameter influencing the river hydrograph (Fig. 5).
The overall assessment of both the surface runoff and river hydrograph results between Case A and B indicates that urban land growth has significantly expediated the increase in surface runoff and river flow peak during a storm. However, this relation between urbanization and urban flooding is not a simple one-to-one relation when the spatial distributions of ISA are very different (e.g., man-made ISA cluster and uniform ISA distributions). This is why there is no significant regression found between the ISA value and the peak value of surface runoff or river hydrograph, when combining the two results from Case A and Case B.
4.2 Results from the HEC-RAS Model
Figure 4-3 shows the differences in flash flood maximum water depth between different simulation cases. The left figure is obtained by deducting the maximum water depth in the year of 1966 from the maximum water depth in the year of 2000, and the right figure is obtained by deducting the maximum water depth in the 0% ISA case from the maximum water depth in the 100% ISA case. Red areas represent maximum water depth increase, and blue areas represent maximum water depth decrease from the year 1966 to 2000 and from 100 to 0% ISA percentage cases. The maps at the middle of Fig. 4-3 show the spatially varied ISA percentage in the years 2000 and 1966. Comparing the two flash flood water difference maps, the right one shows less spatial variation, due to the uniform land use assumption in the Case B. However, the difference map based on real land use maps between the years of 2000 and 1966 has apparent spatial variations. Specifically, sub-basins on the northwestern upstream area experience more flash flood increase than those in the middle to southern downstream area, as the upper-left sub-basins experience greater increase in ISA than the middle to lower part. Although the sub-basins in the lower part of the study area experienced less ISA increase during the time interval, they are influenced by upstream urbanization and also show increases in flash flood extent. Due to the hydrologic connectivity, the middle part of the downstream area (yellow circle) experience less impacts on flood peak and timing than the lake front area (green circle).
Furthermore, in the right difference map between the 100% and 0% ISA percentages cases, the decrease in flash flood extent from 100 to 0% ISA (blue areas) is barely detectable. However, in the real land use data case on the left, some areas experienced noticeable decreases in flash flood maximum water levels. It is possible that land use changes diverted water and led to decreases in maximum water depth in certain areas. In three black circles, the most significant differences between the year 1966 and 2000 were conversion from agricultural land (1966) into commercial areas (2000), reducing the land surface roughness values. This likely had the effect of allowing flash flood waters to move quickly through the new commercial areas (Fig. 6).
Figure 4-4 shows the difference in floodplain maximum water depths between different simulation cases. The left figure is obtained by deducting the maximum water depth in the year 1966 from the maximum water depth in the year of 2000, and the right figure is obtained by deducting the maximum water depth in the 0% ISA case from the maximum water depth in the 100% ISA case. Red areas represent maximum water depth increase, and blue areas represent maximum water depth decrease from the year 1966 to 2000 or from 100 to 0% ISA percentage cases. It can be noticed that floodplains experience expansion when ISA percentages grow. The floodplain difference between the year 2000 and 1966 shows the highest water depth increase in downstream side near the river confluence in black circle. The floodplain difference between the 100% and 0% ISA percentages shows the highest water depth increase in the upstream side in the green circle (Fig. 7).
5 Discussions
5.1 Results from HEC-HMS
Near-linear relations between the surface runoff rate and impervious surface percentage can be found for the four selected sub-basins in Sect 4.1.1 Sub-basin surface runoff for both Case A and Case B scenarios. The slope and R-squared values of the linear regressions are listed in Table 1. The high R-squared values suggest good correlation between these two variables. The slopes of the linear regressions represent the increase in surface runoff rate by each 1% increase in ISA percentage. It can be seen that the Case B results have much higher slopes than in Case A. The reason for the higher normalized slopes in the Case B may lie in the assumption of uniform land use.
Near-linear relations can be found for the selected example river locations in 4.1.2 River hydrograph for both Case A and Case B. The slope and R-squared values of the linear regressions are listed in Table 2. The high R-squared values suggest good correlation between these two variables. The slopes of the linear regressions represent the increase in river flow rate by each 1% increase in ISA percentage. The downstream locations had more river flow rate increase than the upstream locations. Among the selected locations, the most downstream point (Location 6) experiences a six to seven times higher river flow rate increase compared to the most upstream point (Location 1). It is noted that the Case B results exhibit higher normalized slopes than the Case A.
It is an interesting finding that we observe strong linear regression between ISA % and the peak value of surface runoff or river hydrograph when results from Case A and Case B are studied separately, while we observe no significant regression between these features when results from Case A and Case B are studied together. This may because that although surface runoff/river hydrograph is governed by both ISA percentage and spatial distribution of land use, but one of them, which from our results seems to be ISA percentage, has more impact than the other. Then when the change in ISA percentage is very big and the spatial distribution of land use is somewhat similar, the impact of the spatial distribution of land use is insignificant. There may be thresholds for the two factors to exert significant impact.
5.2 Results from HEC-RAS
Although the HEC-RAS model calculates the water depths and velocities during the entire rainfall event, only the maximum water depth maps of flash flooding and floodplain are discussed here, since this result is straightforward for comparison. Table 3 summarizes key attributes of the flash flood and floodplain maps. For the flash flood maps covering 1966 to 2000, the flood-influenced area increased by 3% and the maximum depth increased by 13 centimeters (cm). For the floodplain maps, from 1966 to 2000, the flood-influenced area increased by 10% and the maximum depth increased by 6 cm. In the flash flood maps, 100% ISA percentage case doubles the influenced areas and maximum depths from the 0% ISA percentage case. In the floodplain maps, the 100% ISA percentage case has flood-influenced areas that are over five times larger than the flood-influenced areas from the 0% ISA percentage case. In terms of similar average ISA percentages, the Case A data appear to result in much higher surface runoff compared to the Case B data. The spatially varied land use distribution tends to aggregate the surface runoff compared to spatially uniform land use. This may relate to the hydrologic connectivity found in different land use patterns. In the flash flood maps, the Case A results show large flood-influenced areas from 1966 whose ISA percentage is only 29.61%. However, the flash flood maps from the Case B show smaller flood-influenced areas than the results from the Case A, at similar ISA percentages. This discontinuity between the Case A and B is not severe in the floodplain maps. This fact indicates that the land use distribution greatly affects the extent of the flash flood and has less effect on the size of floodplain extent.
6 Conclusions
This research provides experiments on the impact of urbanization on urban flooding, which assists the understanding of this specific factor in urban flooding. Six land use maps from different years (1966, 1971, 1976, 1981, 1986, and 2000) and six simulated conditions (0%, 20%, 40%, 60%, 80% and 100% ISA percentages) were input into the hydrologic/hydraulic models, in order to generate both flash flood and floodplain maps. Positive linear relations are found between the surface runoff rate/river outflow rate and ISA percentage in experiments. Specifically, urbanization leads to the increase in peak discharge and shortens the time before the peak arrives during an event. The influenced areas by the flash flood and floodplain expand due to continuous urbanization. The downstream areas exhibited higher flood depth increases and larger flood extent increases than the upstream areas due to urbanization in the contributing areas. With the same average ISA percentage, the spatially varied land use may aggregate the flash flood condition compared to spatially uniform land use. This fact may be due to the different hydrologic connectivity in the two groups of cases. The flash flood and floodplain results from the simplified hydrologic/hydraulic models share some patterns found in the real flooding events as well as results from other flood models. The result from this research proves that urbanization has worsened urban flooding to a great extent. With the cumulated damage from continuous urbanization, the severity of urban flooding is expected to increase. In the end, it is worth noting that such promising results also come with affordable computation times. As detailed flood modeling may take days to run in large areas, the simplified models used in this research only takes as little as four hours for the flash flood modeling and 20 min for the floodplain mapping for an area of 367 km2.
Notes
Impervious surface are mainly artificial structures that are covered by impenetrable materials such as asphalt, concrete, brick, and stone.
Hydraulic roughness is the measure of the amount of frictional resistance water experiences when passing over land and channel features, which closely relates to land use types.
References
Al-Ghamdi KA, Elzahrany RA, Mirza MN, Dawod GM (2012) Impacts of urban growth on flood hazards in Makkah City, Saudi Arabia. Int J Water Resour Environ Eng 4:23–34
Anderson DG (1970) Effects of urban development on floods in northern Virginia. US Government Printing Office
Apel H, Trepat OM, Hung NN, Merz B, Dung NV (2016) Combined fluvial and pluvial urban flood hazard analysis: concept development and application to Can Tho city, Mekong Delta, Vietnam. Nat Hazards Earth Syst Sci 16:941–961
Armenakis C, Nirupama N (2014) Flood risk mapping for the city of Toronto. Proc Econ Finance 18:320–326
Banasik K, Pham N (2010) Modelling of the effects of land use changes on flood hydrograph in a small catchment of the Płaskowicka, southern part of Warsaw, Poland. Ann Warsaw Univ Life SciSGGW Land Reclam 42:229–240
Berezowski T, Chormański J, Batelaan O, Canters F, Van de Voorde T (2012) Impact of remotely sensed land-cover proportions on urban runoff prediction. Int J Appl Earth Obs Geoinf 16:54–65
Booth DB (1991) Urbanization and the natural drainage system–impacts, solutions, and prognoses
Bronstert A, Bárdossy A, Bismuth C, Buiteveld H, Disse M, Engel H, Fritsch U, Hundecha Y, Lammersen R, Niehoff D (2007) Multi-scale modelling of land-use change and river training effects on floods in the Rhine basin. River Res Appl 23:1102–1125
Chen AS, Djordjević S, Leandro J, Savić D (2010) An analysis of the combined consequences of pluvial and fluvial flooding. Water Sci Technol 62:1491–1498
Cronshey R (1986) Urban hydrology for small watersheds. US Dept. of Agriculture, Soil Conservation Service, Engineering Division
Dingman SL (2015) Physical hydrology. Waveland Press
Espey WH Jr, Morgan CW, Masch FD (1966) Study of some effects of urbanization on storm runoff from a small watershed. Texas Water Development Board
Hashemyan F, Khaleghi M, Kamyar M (2015) Combination of HEC-HMS and HEC-RAS models in GIS in order to Simulate Flood (Case study: khoshke Rudan river in Fars province, Iran). Res J Recent Sci 4:122–127
Hollis G (1974) The effect of urbanization on floods in the Canon’s Brook, Harlow, Essex. In: Fluvial processes in instrumented watersheds. Institute of British Geographers, London, UK, pp 123–139
Hollis G (1975) The effect of urbanization on floods of different recurrence interval. Water Resour Res 11:431–435
Huang Q, Wang J, Li M, Fei M, Dong J (2017) Modeling the influence of urbanization on urban pluvial flooding: a scenario-based case study in Shanghai, China. Nat Hazards 87:1035–1055
Kellershohn D (2016) Reducing flood risk in Toronto. Institute for Catastrophoc Loss Reduction Forum
Khaghan AAM, Mojaradi B (2016) The Integrate of HEC-HMS and HEC-RAS Models in GIS Integration Models to Simulate Flood (Case Study: the Area of Karaj). Curr World Environ 11:1
Kinosita T, Sonda T (1971) Change of runoff due to urbanization. In Publication of: Airport Forum.
Martens L (1966) Flood inundation and effects of urbanization in metropolitan Charlotte [North Carolina]: US Geol. Survey Open-File Rept 54
Moscrip AL, Montgomery DR (1997) Urbanization, flood frequency, and Salmon abundance in Puget lowland streams 1. JAWRA J Am Water Resour As 33:1289–1297
Nirupama N, Armenakis C, Montpetit M (2014) Is flooding in Toronto a concern? Nat Hazards 72:1259–1264
Patra JP, Kumar R, Mani P (2016) Combined fluvial and pluvial flood inundation modelling for a project site. Proc Technol 24:93–100
Prosdocimi I, Kjeldsen T, Miller J (2015) Detection and attribution of urbanization effect on flood extremes using nonstationary flood-frequency models. Water Resour Res 51:4244–4262
Rossman LA (2010) Storm water management model user’s manual, version 5.0. National Risk Management Research Laboratory, Office of Research and Development, US Environmental Protection Agency Cincinnati
Verbeiren B, Van de Voorde T, Canters F, Binard M, Cornet Y, Batelaan O (2013) Assessing urbanisation effects on rainfall-runoff using a remote sensing supported modelling strategy. Int J Appl Earth Obs Geoinf 21:92–102
Villarini G, Smith JA, Serinaldi F, Bales J, Bates PD, Krajewski WF (2009) Flood frequency analysis for nonstationary annual peak records in an urban drainage basin. Adv Water Resour 32:1255–1266
Water M (2010) MUSIC Guidelines; Recommended input parameters and modelling approaches for MUSIC users. State Government of Victoria, Melbourne
Yin J, Yu D, Yin Z, Wang J, Xu S (2015) Modelling the anthropogenic impacts on fluvial flood risks in a coastal mega-city: a scenario-based case study in Shanghai, China. Landscape Urban Plan 136:144–155
Yu D, Lane SN (2006a) Urban fluvial flood modelling using a two-dimensional diffusion-wave treatment, part 1: mesh resolution effects. Hydrol Process Int J 20:1541–1565
Yu D, Lane SN (2006b) Urban fluvial flood modelling using a two-dimensional diffusion-wave treatment, part 2: development of a sub-grid-scale treatment. Hydrol Process Int J 20:1567–1583
Zhang Y, Guindon B, Sun K (2010) Measuring Canadian urban expansion and impacts on work-related travel distance: 1966–2001. J Land Use Sci 5:217–235
Zhang Y, Guindon B, Sun K (2015) Spatial-temporal-thematic assimilation of Landsat-based and archived historical information for measuring urbanization processes. J Land Use Sci 10:369–387
Zhao G, Gao H, Cuo L (2016) Effects of urbanization and climate change on peak flows over the San Antonio River Basin, Texas. J Hydrometeorol 17:2371–2389
Acknowledgement
This research was supported by the Public Safety Canada through the Water Program of Canada Centre of Mapping and Earth Observation, Natural Resources Canada.
Funding
This research was supported by the Public Safety Canada through the Water Program of Canada Centre of Mapping and Earth Observation, Natural Resources Canada.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
There is no conflict of interest that we know of for this work.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Feng, B., Zhang, Y. & Bourke, R. Urbanization impacts on flood risks based on urban growth data and coupled flood models. Nat Hazards 106, 613–627 (2021). https://doi.org/10.1007/s11069-020-04480-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-020-04480-0