Abstract
Empirical vulnerability models are fundamental tools to assess the impact of future earthquakes on urban settlements and communities. Generally, they consist of sets of fragility curves that are derived from georeferenced post-earthquake damage data. Following the 2015 Nepal earthquake sequence, the World Bank, through the Global Program for Safer Schools, conducted a Structural Integrity and Damage Assessment (SIDA) of about 18,000 school buildings in the earthquake-affected area. In this work, the database is utilized to identify the main structural characteristics of the Nepalese school building stock. For the first time, extended SIDA school damage data is processed to derive fragility curves for the main structural typologies. Data sets for each structural typology are used for a Bayesian updating of existing fragilities to obtain regional models for Nepalese schools. These fragility estimates can be adopted to assess potential seismic losses of the school infrastructure in Nepal. Additionally, they can be used for calibrating loss assessment studies in the wider Himalayan region where the structural typologies are similar.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
According to the last Global Assessment Report on Disaster Risk Reduction (UNDRR 2019), since 1990, 92% of human losses from natural disasters have occurred in low-to-middle-income countries. Low-income nations, with limited resilience against catastrophes, have also sustained larger relative asset losses with respect to advanced economies. Earthquakes, on average, have accounted for 20% of annual economic losses due to natural catastrophes. Despite those figures, international development aid for disaster risk reduction still represents a slim percentage (3.8%) of the funding that is made available for post-disaster response.
As outlined in the Sendai Framework (UNISDR 2015), “while the drivers of disaster risk may be local, national, regional or global in scope, disaster risks have local and specific characteristics that must be understood for the determination of measures to reduce disaster risk”. This is particularly valid in low-income contexts where risk data scarcity remains a major issue (Robinson et al. 2018), and there is a tendency to perform risk assessments with models from other regional contexts. Referring to the education sector, a consistent effort has been put by the World Bank in addressing these aspects with the implementation of the Global Program for Safer Schools (GPSS) (World Bank 2017). Launched in 2014, the GPSS contributes to the Comprehensive School Safety Framework (UNDRR 2017) by financing and advising governments to implement safer school programs worldwide.
In response to the last 2015 (Gorkha) Nepal seismic sequence (Chiaro et al. 2015; EERI Earthquake Engineering Research Institute 2016; Sharma et al. 2016), the GPSS supported the Department of Education of Nepal and trained 150 local engineers to conduct a large-scale Structural Integrity and Damage Assessment (SIDA). Approximately 18,000 school buildings located in the Earthquake-Affected Area (EAA) have been surveyed and the related information has been stored in a georeferenced database.
Post-earthquake damage data represents an important element to develop and validate vulnerability models in the form of vulnerability or fragility curves (Rossetto et al. 2014; Lallemant et al. 2015). Fragility curves express the probability of physical damage with respect to a relevant seismic intensity measure (IM) (e.g., peak ground acceleration, PGA) while vulnerability curves are relationships between seismic loss (e.g., repair cost) and IM. Vulnerabilities can be directly derived from fragility curves by means of damage-to-loss consequence models (Rossetto et al. 2014).
In the Nepalese context, few empirical studies on residential buildings are available (Didier et al. 2017; Gautam et al. 2018) while reliable models for predicting school buildings fragility are currently lacking. This represents a limitation towards the implementation of comprehensive risk and loss assessment studies of school facilities (e.g., O’Reilly et al. 2018, Perrone et al. 2020). By processing the valuable damage information contained in SIDA, this work provides new observational fragility curves for the Nepalese school building stock that can be integrated into earthquake loss assessment platforms (Pagani et al. 2014). Different statistical methods are tested for fragility derivation and the main challenges in conducting empirical studies in data-scarce regions are discussed. Since the data (1) refers to a single earthquake event and (2) is insufficient to derive fragilities for each structural typology with traditional statistical techniques, a Bayesian approach has been undertaken to update existing analytical fragility models from the HAZUS database (Federal Emergency Management Agency 2015). The outcome is a set of new fragility curves that incorporates the information from SIDA and greatly enriches the understanding of schools’ vulnerability in Nepal.
2 Existing empirical fragility estimates for the Nepalese building stock
Despite the multitude of post-disaster surveys conducted in the aftermath of the 2015 Nepal earthquake (Lallemant et al. 2017b), damage data are still hardly accessible, incomplete and sometimes conflicting. Therefore, over the last five years, a consistent number of studies have focused on developing building fragility models by adopting analytical/numerical techniques (Guragain 2015; Chaulagain et al. 2016; Giordano et al. 2019, 2020). This approach has been also followed by GPSS that provides guidelines for analytical derivation of fragility/vulnerability curves for archetype school buildings (World Bank 2019a).
To the best of the author’s knowledge, only two empirical studies are currently available in technical-scientific journals. The first one, by Didier et al. (2017), presents empirical fragility curves for residential buildings by adopting a damage dataset of 30,000 buildings affected by the 2015 Gorkha earthquake. Specifically, a Bayesian procedure is implemented to update a set of prior analytical/opinion-based fragility curves. Four structural typologies are presented: adobe, brick in mud mortar unreinforced masonry (URM), brick in cement mortar URM and reinforced concrete (RC) frames. Three damage states (DSs) are considered in the study (here indicated as DS#D):
-
DS1D: no damage;
-
DS2D: partially damaged;
-
DS3D: collapsed or unrepairable.
Due to the geospatial inhomogeneity of the dataset (i.e., inspected buildings are concentrated in certain areas and are not uniformly distributed over the entire range of seismic intensities), only two out of three DS fragilities are updated with empirical evidence. Table 1 reports median η and lognormal standard deviation β of the PGA lognormal distributions.
Observational fragilities for Nepali residential buildings are also reported in Gautam et al. (2018) with reference to three construction classes: RC frames, brick masonry and stone masonry constructions. The work adopts damage information from seven historical Nepali earthquakes occurred over the last 90 years, namely the 1934 Bihar-Nepal earthquake, 1980 Chainpur earthquake, 1988 Eastern Nepal earthquake, 2011 Eastern Nepal earthquake and the 2015 Gorkha earthquake. The results, expressed in PGA, consider three DSs (DS#G):
-
DS1G: slight to minor damage;
-
DS2G: moderate damage;
-
DS3G: extensive damage to collapse.
It should be noted that aggregated data from historical Himalayan earthquakes are likely to be inaccurate, non-georeferenced, and/or poorly correlated with seismic IMs. Therefore, these fragility curves must be used carefully. Table 1 reports the results of the study where DS2G and DS3G are considered equivalent to DS2D and DS3D.
3 The World Bank’s SIDA database
The World Bank’s SIDA database was developed in the aftermath of the 2015 Gorkha earthquake and includes the georeferenced information of 17,595 school buildings from kindergarten to higher secondary school (Fig. 1a). As shown in Fig. 1b, the capacity of the inspected buildings is highly variable and ranges from less than 10 students/building to hundreds of students/building. Apart from the post-disaster damage assessment purpose, SIDA contributes to the Global Library of School Infrastructure (GLoSI), an online open-access repository of evidence-based knowledge and information about taxonomy and vulnerability of school facilities worldwide (World Bank 2019b). Four main data classes are included in SIDA:
-
School general details name, education facility code, district, address, geographical coordinates, type (public/private), level (grade), number of students, school contacts, etc.
-
Exposure travel time to the closest source of building materials, distance from river/body of water, flooding risk information, landslide risk information, topography, distance to main road and road condition, etc.
-
Physical planning number of school buildings on campus, number of temporary learning centers, owner of school campus land, number of toilets, availability of drinking water, electricity supply, sketch of the site plan and indication of the school buildings, etc.
-
Building assessment damage state, usability, year of construction, primary funders, building constructor (community/contractor), history of additions and modifications, retrofitting information, smallest gap between buildings, access to the building, in-plan shape, irregularity, number of stories, structural category, foundation type, floor/roof type, etc.
For the purpose of this work, mainly damage and structural typology data is discussed. Interested readers are invited to access the GLoSI database for additional information on school facilities in Nepal (World Bank 2019b).
3.1 Description of the school building stock
In SIDA, Nepali school buildings are classified in five main structural typologies. This classification, based on an original work by the National Society for Earthquake Technology, NSET (2000), is extensively described in the reference GPSS document (ARUP 2015) and in a related paper (De Luca et al. 2019). In summary, the following typologies are considered:
-
Masonry (URM) buildings are realized with different combinations of units and joints: brick in cement mortar, brick in mud mortar, Compressed Stabilized Earth Block (CSEB) in mud mortar, dry stones, stone in cement mortar, stone in mud mortar, and stone in mud mortar with cement mortar pointing. Adobe structures complete the set of unreinforced construction types.
-
RC Frame buildings are engineered/non-engineered reinforced concrete structures with brick masonry infill walls.
-
Steel Frame buildings are light-gauge metallic frames, usually regular in plan, where perimeter walls are realized with stone/brick units in mud/cement mortar depending on the local availability of materials.
-
Timber Frame buildings are braced timber frames with bamboo and mud infills.
-
Mixed Structure buildings are combinations of different typologies which frequently results from incremental building construction practices (Lallemant et al. 2017a). SIDA includes four main mixed structure types: RC-masonry, RC-steel, steel-masonry and timber-masonry.
A sample of the information included in SIDA has been cross-validated using the SAFER database of school buildings (Sextos and Mason 2018). This dataset has been developed by the University of Bristol under the UK Global Challenges Research Fund-Engineering and Physical Science Research Council “Seismic Safety and Resilience of Schools in Nepal” project (www.safernepal.net). It gathers georeferenced information by means of a mobile app that is developed for rapid pre- and post-earthquake visual inspection. Data is automatically uploaded on a twin WebApp that facilitates visualization, data processing and risk assessment decision making for prioritizing school portfolios for potential retrofit. Since the first release of the mobile app in 2018 (freely available for download on Android mobile phones https://play.google.com/store/apps/details?id=uk.ac.bristol.rit.safer), approximately 400 school buildings have been inspected thanks to in-field surveys carried out by the National Society for Earthquake Technology (NSET) and Save The Children in several districts. The validation has been carried out by comparing name of the school, education facility code (EMIS number), geographic location and structural typology. Figure 2 comparatively illustrates sample data from three school buildings in Sindhupalchwok retrieved from both SIDA and SAFER databases. Data also includes school name, location, building identification number and construction typology used in the two databases. Interestingly, the information obtained from the first and second set of inspections complement each other since correspond to a post-earthquake (2015) and a pre-future earthquake (2019) assessment, respectively.
Shree Pachkanya Primary School (EMIS230350008, Building A)—RC frame typology: a SIDA, d SAFER. It can be observed that the earthquake damage detected in 2016 by SIDA surveyors has been subsequently repaired as shown in the SAFER database. Shree Narayan Devi Higher Secondary School (EMIS280330001, Building B)—Masonry typology: b SIDA, e SAFER. Seti Devi Higher Secondary School (EMIS230770009, Building D)—steel frame typology: c SIDA, f SAFER
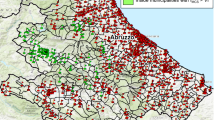
Figure 3 shows the geographical distribution of the building typologies over the fourteen districts of the EAA. The corresponding data breakdown is given in Table 4 of “Appendix”. URMs represent the vast majority of the school building inventory (54.5%) followed by steel frames (26.4%), RC frames (10.7%) and timber frames (2.4%). On the contrary, mixed structures represent a negligible portion of the school building stock. These figures compare reasonably well with previous statistics available in the literature. For instance, on a sample of 909 school buildings located in the Kathmandu Valley, NSET (2000) has found that more than 60% are URMs, while steel and RC buildings account for 22% and 8% of the total. More recently the Asian Development Bank (2014) has estimated that 34% and 5% of the total school building stock are URM-brick buildings and RC frames, respectively. 61% of the buildings belong instead to other structural typologies (e.g., URM-stone, timber frame). The high number of URMs that characterizes the Nepali building stock is also reflected by statistics of residential constructions. In the dataset used by Didier et al. (2017), the aggregated percentage of brick and stone URMs is 59%. Residential RC frames account for 38% of the total database, close to what has been reported by Chaulagain et al. (2016) for the Kathmandu Valley.
Looking at the distribution by district, Dhading, Nuwakot, Sindupalchwok and Kavre are the ones with the largest number of school buildings, each including around 1700 structures (around 10% of the total). Rasuwa is instead the less school-populated district with just 249 buildings. Masonry is the most frequent typology in the majority of the districts with exception of Kavre, Laliptur, and Ramechap where steel frames are more frequent. As expected, the district of Kathmandu has a significant number of RC frames in proportion to the other building classes.
To better understand the composition of the masonry building portfolio, Fig. 4a depicts the percentage distribution of masonry sub-typologies. Brick in cement, brick in mud, stone in cement and stone in mud buildings account for 12%, 3%, 4% and 31% of the total respectively. Stone in mud with cement mortar pointing buildings represent 15% of the total. An important portion of the surveyed URMs has incomplete data (34%). Figure 4b shows the percentage distribution of SIDA buildings with respect to in-plan shape and regularity. About 90% of the structures are characterized by compact/elongated rectangular plans. Lastly, Fig. 4c reports the percentage breakdown by number of stories. Most of the school buildings, 85%, are single-story, while 12% are two-story.
3.2 Seismic damage data
The Damage States adopted in the World Bank’s SIDA database (DS#SIDA) are consistent with the European Macroseismic Scale classification (Grünthal 1998) and are defined as follows:
-
DS0SIDA: unaffected building (no damage);
-
DS1SIDA: minor/cosmetic damage only;
-
DS2SIDA: damage to non-structural components; no threat to structural stability
-
DS3SIDA: damage to structural components and/or infill walls for RC/steel frames with infills;
-
DS4SIDA: partial collapse;
-
DS5SIDA: collapse.
Figure 5 reports the geospatial damage distribution of URM structures that corresponds to 9587 buildings. It shows that URMs are homogeneously distributed over the EAA with a slightly higher density in the northern districts. In these same districts (namely, Gorkha, Dhading, Nuwakot and Sindhupalchwok), the largest number of collapses was recorded but this, of course, relates to the high intensity of seismic shaking. Masonry school buildings located in urbanized areas (Kathmandu, Lalitpur and Bhaktapur) were mostly undamaged or experienced minor-to-moderate damage. The percentage breakdown of DS over the EAA is 13% for DS0SIDA, 15% for DS1SIDA, 3% for DS2SIDA, 32% for DS3SIDA, 7% for DS5SIDA and 30% for DS5SIDA.
Figure 6 shows the geospatial distribution of DSs for RC frame typology (1878 buildings). In this case, buildings are not uniformly distributed across the EAA resulting in a consistent concentration of RC frames in and around Kathmandu. Generally, the damage experienced by RC frame schools was rather low. In particular, 41% of these buildings were undamaged, while 24%, 3% and 28% experienced a level of damage between DS1SIDA to DS3SIDA, respectively. Lastly, less than 4% of RC school buildings sustained partial or total collapse (i.e., DS4SIDA, DS5SIDA). The low percentage of collapses is also a direct consequence of the relatively low ground shaking experienced in the Kathmandu Valley with respect to the rural districts.
Steel frames’ DS geospatial distribution is shown in Fig. 7 (4651 buildings). Most of these school buildings are concentrated in the north-east part of the EAA (Sindhupalchwok, Ramechap and Kavre) while they are rather uncommon in the southern part. As indicated in several post-earthquake reconnaissance reports (e.g., EERI Earthquake Engineering Research Institute 2016), these constructions were mostly affected by damage of the masonry infill walls. This observation is reflected in SIDA where most of the school buildings (47%) experienced DS3SIDA. The exact breakdown of DS for the steel frame typology is: 21% for DS0SIDA, 15% for DS1SIDA, 7% for DS2SIDA, 47% for DS3SIDA, 8% for DS4SIDA and 3% for DS5SIDA.
Lastly, Fig. 8 reports the damage geospatial distribution for timber frame typology (424 buildings). The vast majority of these buildings are located in the southern part of the EAA (districts of Makwanpur and Sindhuli) and naturally, experienced light to moderate damage. In particular, 30% DS0SIDA, 17% DS1SIDA, 9% DS2SIDA, 33% DS3SIDA, 8% DS4SIDA and 3% DS5SIDA.
4 Empirical fragilities derived from SIDA
The first step to derive empirical fragility curves is to quantify the severity of seismic shaking for each building of the dataset (e.g., De Luca et al. 2018). In this way, georeferenced damage information can be correlated with spatial distribution of ground motion IMs such as PGA. This requires the adoption of “shake maps” which are the combined result of instrumental measurements, information about local geology, earthquake location and magnitude (Wald et al. 2006). Once damage and shake intensity information are paired, fragility curves are estimated through statistical regression procedures (Rossetto et al. 2014). Obviously, the validity of the results relies on the quality of input data, which is particularly challenging when working on data-scarce regions like Nepal (Robinson et al. 2018).
4.1 Shake maps of the 2015 Nepal earthquake sequence
At the time of the 2015 mainshock only a limited number of seismic recording stations were operating in Nepal, mainly concentrated in the city of Kathmandu. Therefore, it is problematic: (1) to evaluate the extent of the area affected by ground shaking and (2) to estimate the variation of the seismic excitation within the area (McGowan et al. 2017). In addition, the limited knowledge on the country’s geology (Gilder et al. 2020) and the lack of representative Ground Motion Prediction Equations (GMPEs) for the region (Bajaj and Anbazhagan 2019) result in large uncertainties on shake maps. In the last five years, the United States Geological Survey (USGS) has released a set of shake maps for the Gorkha sequence, progressively updated to include more advanced studies (McGowan et al. 2017). In this work the following USGS maps are considered:
-
M 7.8—36 km E of Khudi, Nepal earthquake (mainshock) occurred on April 25th 2015 (USGS 2017a);
-
M 7.3—19 km SE of Kodari, Nepal earthquake (aftershock) occurred on May 12th 2015 (USGS 2017b).
These two shake maps are illustrated in Fig. 9a, b, where it is evident that the mainshock affected a larger area with respect to the aftershock. In terms of intensity, the April 25 shake map had a maximum PGA of 1.0 g, while the value for the May 12 event reached 0.85 g. Given the absence of disaggregated information on the damage generated by mainshock and aftershock (SIDA surveying activities began after May 12), PGA values at individual building locations are extracted from the maximum envelope of the two shake maps (Fig. 9c). This simplification, though inevitable due to lack of data, cannot take properly into account the effect of aftershocks (Dong and Frangopol 2015) and most importantly, the sequence of nonlinear incremental damage (particularly relevant for masonry buildings (Sextos et al. 2018)).
In this study, PGA is selected as the IM for the derivation of empirical curves. This choice is motivated by four reasons. First, PGA is usually a good predictor for stiff structures (Silva et al. 2019) such as one-story buildings [85% of SIDA (Fig. 4c)]. Second, PGA is preferred to spectral quantities (such as the spectral acceleration at the fundamental period of the structure Sa(T1)) given the consistent lack of attenuation equations of spectral ordinates for the Himalayan region (e.g., Bajaj and Anbazhagan 2019). Third, the use of spectral values would require the estimation of an average fundamental period for each SIDA building class through empirical equations, which would subsequently add a degree of epistemic uncertainty to the problem (Rossetto et al. 2014). Forth, PGA is a commonly used IM in vulnerability models (Calvi et al. 2006) and was selected in previous fragility studies for Nepal (Didier et al. 2017; Gautam et al. 2018; Giordano et al. 2019).
4.2 Empirical fragility estimates for masonry school buildings
Once damage and seismic intensity at building locations are defined, fragility curves that express the probability of exceedance of different DSs can be derived adopting statistical regression methods (Rossetto et al. 2014). As a first step, building data must be aggregated in representative building classes which are characterized, for instance, by same structural typology and number of stories. The definition of classes should strike a balance between granularity (i.e., more classes result in a better description of the building stock vulnerability) and size of the corresponding sub-datasets (statistical regressions on small datasets can lead to meaningless results). To guarantee sufficiently large sub-datasets of building classes, four classes are defined to match the four main SIDA structural typologies. Another aspect to be considered when deriving fragilities from observational data is the spatial distribution of the dataset. Several studies have shown that spatially inhomogeneous datasets (i.e., buildings concentrated in areas where the range of variation of PGA is limited) can lead to inconsistent results (De Luca et al. 2018). In these cases, Bayesian updating procedure of existing fragility curves should be adopted (Singhal and Kiremidjian 1998; Miano et al. 2016). Given the observations presented in 3.2., only masonry school data is sufficient to derive fragilities with standard statistical methods, while fragility estimates for other structural typologies are made by means of the Bayesian method as discussed in the following section.
Observational fragilities for masonry school buildings are calculated with the Maximum Likelihood Estimation (MLE) method. MLE is one of the most widely adopted techniques for deriving empirical fragility curves and it has been used to assess the performance of numerous structural types in different regional contexts (Shinozuka et al. 2000; Colombi et al. 2008; De Luca et al. 2015; Del Gaudio et al. 2019). The first step of MLE consists of subdividing the dataset in ranges of PGA (bins) for which the Damage State exceedance probabilities are computed (Fig. 10a). Each of these bins should contain the same amount of buildings (Porter et al. 2007). Subsequently, given a probability distribution function (PDF) model, MLE permits the evaluation of the PDF parameters that maximize the probability of occurrence of the observed data (Lallemant et al. 2015). If the fragility curve is represented by a lognormal model, the estimates \(\hat{\mu }_{log}\) and \(\hat{\beta }\) of the logarithmic mean \(\mu_{log}\) and standard deviation \(\beta\) are given by the following expression:
where m is the number of bins, PGAi is the average peak ground acceleration of the ith bin, ni is the number of buildings reaching or exceeding the considered DS in the ith bin, Ni is the total number of buildings in the ith bin, Φ(·) is the standard normal cumulative distribution function. The result of the MLE method can be graphically represented in the form of a linear regression as shown in Fig. 10b. Particularly, x is the logarithm of PGAi and y is the inverse standard normal distribution of (ni + 1)/(Ni + 1). The resulting fragility curves are shown in Fig. 11 (DS#-MLE), while corresponding statistical parameters are summarized in Table 2.
Empirical fragility curves for school masonry buildings. Solid lines represent fragilities derived with the MLE method, while dashed lines are fragilities estimated with the MLE procedure as modified by Porter et al. (2007)
From Fig. 10b it is observed that the MLE method can lead to inconsistent results when fragility curves of consecutive DS cross with each other. These situations can be avoided by adopting a constant lognormal standard deviation (Porter et al. 2007):
and updated values for the median PGAs:
Resulting fragility curves are shown in Fig. 11 (DS#-MLE n.c.), while relative statistical parameters are included in Table 2.
4.3 Bayesian updating of existing fragility models for different structural typologies
Bayesian Updating (BU) techniques are effective alternatives to traditional statistical methods when dealing with small or spatially inhomogeneous observational damage datasets. Several studies have suggested the adoption of Bayesian techniques to update preexisting fragility curves (e.g., Singhal and Kiremidjian 1998; Miano et al. 2016; De Risi et al. 2017; De Luca et al. 2018). As mentioned in the introduction, a Bayesian approach has been also used by Didier et al. (2017) in the context of Nepal, but the analysis was solely focused on residential buildings and did not include schools. Two main set of information are required to perform a Bayesian updating: the prior probabilistic model and the likelihood function of the empirical data (Singhal and Kiremidjian 1998). Subsequently, by applying the Bayes theorem, the probabilistic parameters of the posterior model are estimated. In details, by referring to the Bayesian regression analysis procedure reported by Faber (2012), the updated regression coefficients \(\varvec{B^{\prime\prime}} = \left( {\begin{array}{*{20}c} {b_{0}^{''} } & {b_{1}^{''} } \\ \end{array} } \right)^{T}\) of a generic linear model \(y = b_{0}^{''} + b_{1}^{''} x\) (such as the ones shown in Fig. 10b) are calculated as follow:
where \(\varvec{B^{\prime}} = \left( {\begin{array}{*{20}c} {b_{0}^{'} } & {b_{1}^{'} } \\ \end{array} } \right)^{T}\) are the regression coefficients of the prior model and \(\hat{\varvec{X}}\), \(\hat{\varvec{y}}\) are matrixes with the coordinates of the new empirical data as defined by Faber (2012).
The selection of the prior fragility models represents a crucial point of the BU procedure. When several structural typologies are considered, it is fundamental to adopt a consistent set of prior curves. Unfortunately, this information is lacking in data-scarce regions like Nepal. For instance, the fragility models presented by Didier et al. (2017) and Gautam et al. (2018) cover exclusively the unreinforced masonry and RC typologies. In addition, these fragilities do not represent a general baseline since were extracted from damage data of residential buildings. Previous vulnerability and risk assessment studies in low-to-middle income contexts have adopted the HAZUS models (Federal Emergency Management Agency 2015) as general reference for building fragility curves. Gentile et al. (2019) have used HAZUS fragilities to define the baseline score of a seismic risk index for school buildings in Indonesia while Sevieri et al. (2020) have extended the approach to the Philippines. HAZUS models have also been used in loss assessment studies in Nepal (Robinson et al. 2018). By analogy with the Uniform Building Code 1994 (ICBO 1994), HAZUS models are subdivided into four seismic code levels: high code, moderate code, low code and pre-code (Gentile et al. 2019). In countries where the building standards have followed the evolution of the UBC, these four levels can be used in full (Sevieri et al. 2020). This is not the case of Nepal where: (1) most of the constructions have been realized according to mandatory rules of thumb rather than engineering design, (2) the first building standard, the Nepal National Building Code (Department of Urban Development and Building Construction 1994) has been effectively enacted in 2003 (Giri et al. 2019). For these reasons, this study refers to low-code and pre-code fragilities exclusively. In details:
-
Masonry unreinforced masonry bearing wall, low-rise (URML), pre-code;
-
RC Frame concrete frame building with unreinforced masonry infill walls, low rise (C3L), low-code;
-
Steel Frame steel light frame (S3), low-code;
-
Timber Frame wood light frame (W1), pre-code.
To account for the poor construction quality of traditional buildings in Nepal, pre-code models (i.e., construction prior to seismic code enforcement) have been considered for masonry and timber frame typologies. RC frame school buildings are generally newer constructions with minimum seismic detailing. Therefore, low (i.e., older) code HAZUS fragilities are considered as prior. Lastly, low-code fragility curves are selected for the steel frame typology. In fact, most of these constructions are fairly designed since were built from 1992 to 1995 under the World Bank’s Earthquake-Affected Areas Reconstruction and Rehabilitation Project (NSET 2000) or, more recently, by the Japan International Cooperation Agency (JICA 2009). It should be noted that the steel light frame typology considered in HAZUS does not exactly correspond to the one of SIDA. In Nepal, perimeter walls are not realized with lightweight panels but with stone/brick units in mud/cement mortar depending on the local availability of materials. Figure 12 reports prior and posterior fragility curves for the four structural typologies. The corresponding probabilistic parameters are given in Table 2. It can be observed that HAZUS fragility curves are defined for four damage states, namely: Slight, Moderate, Extensive and Collapse. Therefore, to execute the BU procedure, the following equivalences with DS#SIDA are considered: DS2SIDA ≈ Slight, DS3SIDA ≈ Moderate, DS4SIDA ≈ Extensive, DS5SIDA ≈ Collapse.
4.4 Discussion of the fragility results
To facilitate the discussion of these results with respect to the existing observational fragilities by Didier et al. (2017) and Gautam et al. (2018), the DS equivalences given in Table 3 are considered.
General comments:
-
1.
Relative fragility of masonry school buildings due to different statistical methods. As expected, for DS1SIDA, the MLE method provides consistently larger median PGA and standard deviation (0.021 g, 2.76) with respect to the MLE n.c. technique (0.006 g, 1.71). Conversely, for DS5SIDA, the MLE method gives conservative and less scattered results (0.97 g, 0.94) with respect to the MLE n.c. (2.59 g, 1.71). The BU method provides the lowest estimates of η and β at any DS. As expected, the intrinsic uncertainties of observational data and the inaccuracy of the shake map (Sect. 4.1.) affect the results of standard statistical methods. Median PGA for high DS appears unrealistically higher than previous analytical results available in the literature (Giordano et al. 2019). In this sense, the BU methodology seems to be an effective way to utilize the valuable set of observational data collected by the World Bank, while maintaining reasonable values for median PGA. Based on this observation the following comparisons focus on the BU method.
-
2.
Masonry buildings fragility (BU method) and comparison with Didier et al. (2017): DS2-3SIDA fragilities are characterized by comparable values of η (0.14 g, 0.18 g) with respect to DS2D brick-mud URM (0.14 g). On the contrary, the median value of DS2D brick-cement URM is consistently higher (0.77 g). Dispersion of DS2D is about two times larger than DS2-3SIDA. Median PGAs of DS4-5SIDA (0.39 g, 0.55 g) are considerably lower than DS2D brick-mud URM (1.26 g) and brick-cement URM (1.90 g). Corresponding β (0.82, 0.76) are comparable with the brick-cement value (0.93) while considerably lower than brick-mud dispersion (1.96). These large discrepancies likely derive from a combination of factors such as data inhomogeneity and differences in prior models. What appears unrealistic is that median PGAs for residential buildings (Didier et al. 2017) are systematically higher than the corresponding estimates for school buildings. In Nepal, residential URMs are usually constructed by homeowners, non-engineered, non-compliant to building regulations and without basic seismic detailing (Gautam et al. 2016). On the contrary, schools are subjected to a stricter code enforcement and the required level of safety is higher with respect to residential structures. The non-uniformity (i.e., non-uniform distribution of buildings in the full range of PGAs) of the database used by Didier et al. (2017) could be a reason for the high dispersions and median values with respect to the SIDA fragilities.
-
3.
Masonry buildings fragility (BU method), comparison with Gautam et al. (2018). DS2-3SIDA present comparable median values with respect to DS1-2G Brick URM (0.13 g, 0.16 g). On the contrary, there is little agreement with respect to the results of DS1-2G Stone URM (0.29 g, 0.32 g). Median values of DS4-5SIDA are fairly similar to DS3G Stone URM (0.39 g) but consistently different from DS3G Brick URM (0.22 g). Theoretically, the empirical curves by Gautam et al. (2018) should be considered the best fragility estimate since they account for damage variability from five past earthquake events. However, these historical datasets inevitably come with large uncertainties on damage data quality, shake maps, and geographical accuracy. It is also surprising that, despite these large uncertainties, dispersion values of DS#G are unexpectedly lower than DS#SIDA.
-
4.
RC Frame buildings fragility (BU method), comparison with Didier et al. (2017). DS2-3SIDA median PGAs (0.19 g, 0.27 g) are systematically lower than the corresponding value for DS2D (1.67 g). The corresponding β (1.08, 1.04) are consistently lower than the value for DS2D (1.73). DS4-5SIDA (0.77 g, 1.13 g) provides a more conservative estimate of η with respect to DS3D (1.95 g). The related dispersions are instead comparable (0.88, 0.84 versus 0.71). Comments of point (2) can be extended to the case of RC.
-
5.
RC Frame buildings fragility (BU method) comparison with Gautam et al. (2018). DS2-3SIDA median PGAs are consistently lower than DS1-2G (0.29 g, 0.63 g). Analogously, median values of DS4-5SIDA are conservative with respect to DS3G (1.29 g). Comments of point (3) can be extended to this comparison.
A further way to compare the existing empirical fragilities with the ones derived in this study is to assess the similarity of two probability distributions with information theory measures. Looking at the literature, some studies in the field of earthquake engineering have adopted the Kullback‐Leibler divergence as a measure of the statistical distance between a real distribution and its approximation (e.g., De Luca et al. 2015; Tsioulou and Galasso 2018). For instance, Tsioulou and Galasso (2018) have compared distributions of IMs from recorded and simulated ground motions. Since the fragility models presented in this study are all “approximations of the reality”, this works adopts the Bhattacharyya distance, DB, (Bhattacharyya 1946) instead of the Kullback‐Leibler divergence. This quantity, which relates to the amount of overlap between two statistical models, is expressed by the following equation:
where p1(x) and p2(x) are two probability distribution functions. From Eq. 6 it can be observed that DB is a nonnegative parameter. Additionally, DB, unlike the Kullback–Leibler divergence, is a symmetric quantity, i.e., DB (p1, p2)= DB (p2, p1). Figure 13 presents a comparison of the three empirical studies in terms of DB at each damage level. Particularly Fig. 13a, b refers to masonry and RC respectively. In the context of this work, the absolute value of DB is informative only when relatively compared with the full set of distances. This last aspect differs from the study by Tsioulou and Galasso (2018) where a procedure to assess the similarity of two distributions from the absolute value of the Kullback‐Leibler divergence is reported.
Bhattacharyya distance DB estimated for different DS (equivalence as for Table 3 is reported on top of each matrix). a Masonry, b RC. The following abbreviations are considered: SIDA = fragility from BU; D = Didier et al. (2017); BM = brick-mud URM; BC = brick-cement URM; G = Gautam et al. (2018); B = brick URM; S = stone URM
The differences in DB values between the three models can be attributed to (i) the non-uniform quality and extension of the damage data, (ii) the different definition of damage states, and (iii) the difference in building characteristics (e.g., school buildings are mainly single-storied, while residential are usually multi-storied), (iv) the different shake map accuracy. The results show that the discrepancy between the empirical models is smaller for RC buildings than for URMs, especially when assessing higher damage states. This is probably an inevitable result of the intrinsic larger uncertainties around the response of non-engineered masonry structures.
5 Conclusions
In this work, a set of empirical-based fragility curves for Nepalese school buildings has been produced by processing the damage information included in the World Bank’s Structural Integrity and Damage Assessment database. These fragilities are related to four relevant structural types: masonry, RC frame, steel frame and timber frame. Firstly, traditional statistical regression methods have been tested for fragility derivation. Subsequently, a Bayesian procedure has been implemented by selecting appropriate prior fragility models and by updating them with the empirical evidence from the 2015 Nepal earthquake sequence. The comparison with two previous empirical studies on Nepali residential buildings (Didier et al. 2017; Gautam et al. 2018) has shown consistent differences in the results. This could be the consequence of (i) different building characteristics between schools and residential, (ii) non-uniform quality of damage/intensity/geographical data, (iii) different statistical approach and damage state definition. From these discrepancies, it is quite difficult to conclude which of the models better represents the reality. This is an answer that could be provided having further empirical references from future earthquakes. In general, the fragility models presented in this work represent the optimal solution when dealing with school building portfolios. The Bayesian approach adopted in this study allowed to incorporate rich observational information in well-established fragility models, obtaining more conservative/realistic damage state probability distributions for the specific case of schools. This appears to be the best strategy in data-scarce contexts where different sources of information are available, but none of them can provide a full understanding of the problem. These new empirical curves can be used in combination with existing analytical models for the region to better characterize the epistemic and aleatory uncertainties, leading to more robust risk assessments at territorial scale and at asset level.
References
ARUP (2015) Global program for safer schools—structural typologies. London, UK
Asian Development Bank (2014) Strategy and plan for increasing disaster resilience for schools in Nepal. Bangkok, Thailand, Thailand
Bajaj K, Anbazhagan P (2019) Regional stochastic GMPE with available recorded data for active region: application to the Himalayan region. Soil Dyn Earthq Eng 126:105825. https://doi.org/10.1016/j.soildyn.2019.105825
Bhattacharyya A (1946) On a measure of divergence between two multinomial populations. Indian J Stat 7(4):401–406
Calvi GM, Pinho R, Magenes G et al (2006) Development of seismic vulnerability assessment methodologies over the past 30 years. ISET J 43:75–104. https://doi.org/10.1109/jstqe.2007.897175
Chaulagain H, Rodrigues H, Silva V et al (2016) Earthquake loss estimation for the Kathmandu Valley. Bull Earthq Eng 14:59–88. https://doi.org/10.1007/s10518-015-9811-5
Chiaro G, Kiyota T, Pokhrel RM et al (2015) Reconnaissance report on geotechnical and structural damage caused by the 2015 Gorkha Earthquake, Nepal. Soils Found 55:1030–1043. https://doi.org/10.1016/j.sandf.2015.09.006
Colombi M, Borzi B, Crowley H et al (2008) Deriving vulnerability curves using Italian earthquake damage data. Bull Earthq Eng 6:485–504. https://doi.org/10.1007/s10518-008-9073-6
De Luca F, Verderame GM, Manfredi G (2015) Analytical versus observational fragilities: the case of Pettino (L’Aquila) damage data database. Bull Earthq Eng. https://doi.org/10.1007/s10518-014-9658-1
De Luca F, Woods GED, Galasso C, D’Ayala D (2018) RC infilled building performance against the evidence of the 2016 EEFIT Central Italy post-earthquake reconnaissance mission: empirical fragilities and comparison with the FAST method. Bull Earthq Eng. https://doi.org/10.1007/s10518-017-0289-1
De Luca F, Giordano N, Gryc H et al (2019) Nepalese school building stock and implications on seismic vulnerability assessment. In: 2nd international conference on earthquake engineering and post disaster reconstruction planning. Bhaktapur, Nepal, pp 319–328
De Risi R, Goda K, Mori N, Yasuda T (2017) Bayesian tsunami fragility modeling considering input data uncertainty. Stoch Environ Res Risk Assess 31:1253–1269. https://doi.org/10.1007/s00477-016-1230-x
Del Gaudio C, De Martino G, Di Ludovico M et al (2019) Empirical fragility curves for masonry buildings after the 2009 L’Aquila, Italy, earthquake. Bull Earthq Eng. https://doi.org/10.1007/s10518-019-00683-4
Department of Urban Development and Building Construction (1994) Nepal national building code. Kathmandu, Nepal
Didier M, Baumberger S, Tobler R et al (2017) Improving post-earthquake building safety evaluation using the 2015 Gorkha, Nepal, earthquake rapid visual damage assessment data. Earthq Spectra 33:S415–S434. https://doi.org/10.1193/112916EQS210M
Dong Y, Frangopol DM (2015) Risk and resilience assessment of bridges under mainshock and aftershocks incorporating uncertainties. Eng Struct 83:198–208. https://doi.org/10.1016/j.engstruct.2014.10.050
EERI Earthquake Engineering Research Institute (2016) M7.8 Gorkha, Nepal Earthquake on April 25, 2015 and its aftershocks. Oakland, CA, USA
Faber MH (2012) Statistics and probability theory—in pursuit of engineering decision support
Federal Emergency Management Agency (2015) Hazus—MH 2.1: technical manual
Gautam D, Rodrigues H, Bhetwal KK et al (2016) Common structural and construction deficiencies of Nepalese buildings. Innov Infrastruct Solut 1:1. https://doi.org/10.1007/s41062-016-0001-3
Gautam D, Fabbrocino G, Santucci de Magistris F (2018) Derive empirical fragility functions for Nepali residential buildings. Eng Struct 171:617–628. https://doi.org/10.1016/j.engstruct.2018.06.018
Gentile R, Galasso C, Idris Y, Rusydy I, Meilianda E (2019) From rapid visual survey to multi-hazard risk prioritisation and numerical fragility of school buildings. Nat Hazards Earth Syst Sci 19(7):1365–1386. https://doi.org/10.5194/nhess-19-1365-2019
Gilder C, Pokhrel RM, Vardanega PJ et al (2020) The SAFER geodatabase for the Kathmandu Valley: geotechnical and geological variability. Earthq Spectra. https://doi.org/10.1177/8755293019899952
Giordano N, De Luca F, Sextos A, Maskey PN (2019) Derivation of fragility curves for URM school buildings in Nepal. In: 13th international conference on applications of statistics and probability in civil engineering, ICASP13. Seoul, South Korea, pp 1–8
Giordano N, De Luca F, Sextos A (2020) Out-of-plane closed-form solution for the seismic assessment of unreinforced masonry schools in Nepal. Eng Struct 203:109548
Giri P, Bhatt AD, Gautam D, Chaulagain H (2019) Comparison between the seismic codes of Nepal, India, Japan, and EU. Asian J Civ Eng 20:301–312. https://doi.org/10.1007/s42107-018-0102-8
Grünthal G (1998) EMS98—European Macroseismic Scale 1998. Luxemburg
Guragain R (2015) Development of earthquake risk assessment system for Nepal. University of Tokyo
ICBO—International Conference of Building Officials (1994) Uniform building code. Whittier, CA, USA
JICA (2009) Primary school construction in support of education for all. https://www.jica.go.jp/nepal/english/activities/education.html. Accessed 2 Feb 2020
Lallemant D, Kiremidjian A, Burton H (2015) Statistical procedures for developing earthquake damage fragility curves. Earthq Eng Struct Dyn 44:1373–1389. https://doi.org/10.1002/eqe
Lallemant D, Burton H, Ceferino L et al (2017a) A framework and case study for earthquake vulnerability assessment of incrementally expanding buildings. Earthq Spectra. https://doi.org/10.1193/011116EQS010M
Lallemant D, Soden R, Rubinyi S et al (2017b) Post-disaster damage assessments as catalysts for recovery: a look at assessments conducted in the wake of the 2015 Gorkha, Nepal, Earthquake. Earthq Spectra 33:435–451. https://doi.org/10.1193/120316eqs222m
McGowan SM, Jaiswal KS, Wald DJ (2017) Using structural damage statistics to derive macroseismic intensity within the Kathmandu valley for the 2015 M7.8 Gorkha, Nepal earthquake. Tectonophysics 714–715:158–172. https://doi.org/10.1016/j.tecto.2016.08.002
Miano A, Jalayer F, De Risi R et al (2016) Model updating and seismic loss assessment for a portfolio of bridges. Bull Earthq Eng 14:699–719. https://doi.org/10.1007/s10518-015-9850-y
National Society for Earthquake Technology (NSET) (2000) Seismic vulnerability of the public school buildings of Kathmandu Valley and methods for reducing it. Kathmandu, Nepal
O’Reilly GJ, Perrone D, Fox M, Monteiro R, Filiatrault A (2018) Seismic assessment and loss estimation of existing school buildings in Italy. Eng Struct 168:142–162. https://doi.org/10.1016/j.engstruct.2018.04.056
Pagani M, Monelli D, Weatherill G et al (2014) Openquake engine: An open hazard (and risk) software for the global earthquake model. Seismol Res Lett. https://doi.org/10.1785/0220130087
Perrone D, O’Reilly GJ, Monteiro R, Filiatrault A (2020) Assessing seismic risk in typical Italian school buildings: from in situ survey to loss estimation. Int J Disaster Risk Reduct 44:101448. https://doi.org/10.1016/j.ijdrr.2019.101448
Porter KA, Kennedy R, Bachman R (2007) Creating fragility functions for performance-based earthquake engineering. Earthq Spectra 23:471–489. https://doi.org/10.1193/1.2720892
Robinson TR, Rosser NJ, Densmore AL et al (2018) Use of scenario ensembles for deriving seismic risk. Proc Natl Acad Sci 115:E9532–E9541. https://doi.org/10.1073/pnas.1807433115
Rossetto T, Ioannou I, Grant D, Maqsood T (2014) Guidelines for the empirical vulnerability assessment. GEM Tech Rep 08:140. https://doi.org/10.13117/GEM.VULN-MOD.TR2014.11
Sevieri G, Galasso C, D’Ayala D, De Jesus R, Oreta A, Grio MEDA, Ibabao R (2020) A multi-hazard risk prioritisation framework for cultural heritage assets. Nat Hazards Earth Syst Sci 20:1391–1414. https://doi.org/10.5194/nhess-20-1391-2020
Sextos A, Mason C (2018) SAFER App technical manual and user’s guide. Bristol, UK
Sextos A, De Risi R, Pagliaroli A et al (2018) Local site effects and incremental damage of buildings during the 2016 central Italy earthquake sequence. Earthq Spectra 34:1639–1669. https://doi.org/10.1193/100317EQS194M
Sharma K, Deng L, Noguez CC (2016) Field investigation on the performance of building structures during the April 25, 2015, Gorkha earthquake in Nepal. Eng Struct 121:61–74. https://doi.org/10.1016/j.engstruct.2016.04.043
Shinozuka M, Feng MQ, Lee J, Naganuma T (2000) Statistical analysis of fragility curves. J Eng Mech 126:1224–1231. https://doi.org/10.1061/(ASCE)0733-9399(2000)126:12(1224)
Silva V, Akkar S, Baker J, Bazzurro P, Castro JM, Crowley H et al (2019) Current challenges and future trends in analytical fragility and vulnerability modelling. Earthq Spectra. https://doi.org/10.1193/042418eqs101o
Singhal A, Kiremidjian AS (1998) Bayesian updating of fragilities with application to RC frames. J Struct Eng 124:922–929. https://doi.org/10.1061/(ASCE)0733-9445(1998)124:8(922)
Tsioulou A, Galasso C (2018) Information theory measures for the engineering validation of ground motion simulations. Earthq Eng Struct Dyn 47(4):1095–1104. https://doi.org/10.1002/eqe.3015
UNDRR (2017) Comprehensive school safety: a global framework in support of the global alliance for disaster risk reduction and resilience in the education sector and the worldwide initiative for safe schools
UNDRR (2019) Global assessment report on disaster risk reduction. Geneva, Switzerland
UNISDR (2015) sendai framework for disaster risk reduction. Geneva, Switzerland
USGS (2017a) M 7.8—36 km E of Khudi, Nepal. https://earthquake.usgs.gov/earthquakes/eventpage/us20002926/executive
USGS (2017b) M 7.3—19 km SE of Kodari, Nepal. https://earthquake.usgs.gov/earthquakes/eventpage/us20002ejl/executive
Wald DJ, Worden BC, Quitoriano V, Pankow KL (2006) ShakeMap manual: technical manual, user’s guide, and software guide. USGS
World Bank (2017) Global program for safer schools. Washington, DC, USA. https://gpss.worldbank.org/
World Bank (2019a) Fragility and vulnerability assessment guide. Washington, DC, USA
World Bank (2019b) Global library of school infrastructure. https://gpss.worldbank.org/en/glosi/about-glosi
Acknowledgements
This work is the result of a partnership between The University of Bristol and The World Bank within the UK Global Challenges Research Fund—Engineering and Physical Science Research Council (GCRF-EPSRC) “Seismic Safety and Resilience of Schools in Nepal—SAFER” project (EP/P028926/1), (http://www.safernepal.net). The World Bank’s Global Program for Safer Schools (https://gpss.worldbank.org) is acknowledged for providing access to the SIDA database. The authors thank Dr Raffaele De Risi for his helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
See Table 4.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Giordano, N., De Luca, F., Sextos, A. et al. Empirical seismic fragility models for Nepalese school buildings. Nat Hazards 105, 339–362 (2021). https://doi.org/10.1007/s11069-020-04312-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-020-04312-1