1 Introduction

Extreme weather-related events can cause significant economic, social, and environmental disruption. In the U.S., it is estimated that flood-related events have generated losses exceeding $124.7 billion and caused 546 deaths since 1980 (NOAA National Centers for Environmental Information (NCEI) 2019). Flood risk has increased substantially during the previous 30 years, growing from approximately $2 bn/year in 1985 to $4 bn/year in 2015. While this increase has been driven in large part by socioeconomic growth in flood prone areas (Changnon et al. 2000; Pielke and Downton 2000; Jongman et al. 2012; Visser et al. 2014), there is a rapidly growing body of literature that suggests that the frequency and intensity of extreme precipitation events in the U.S. is also increasing due to anthropogenic climate change resulting in larger flood hazards, more exposure, and less lead time prior to an event (IPCC 2012; USGCRP 2018). To better prepare for and mitigate future losses, it is important to understand changing spatial and temporal patterns in precipitation extremes.

U.S. flood risk reduction (FRR) policy is centered around the 1% flood hazard and, in fewer instances, the 0.2% flood hazard. The area inundated by a 1% flood is known as the Special Flood Hazard Area (SFHA). This deterministic boundary is used to set flood insurance premiums and guide local planning and development decisions (Highfield et al. 2013; Blessing et al. 2017). Where extreme precipitation is a major driver of riverine flooding, the SFHA is modeled using a design precipitation event, also known as a design storm. Conventionally, a design storm is based on a precipitation frequency (PF) estimate for a 24-hr event that has a 1% chance of annual occurrence derived from statistical analyses of historical observations at nearby rain gauges. However, the intensity–duration–frequency (IDF) curves used to generate design storms are updated infrequently (see, e.g., Weather Bureau Technical Paper No. 40 (Hershfield 1961), NOAA Technical Memorandum NWS HYDRO-35 (Frederick et al. 1977) and NOAA Atlas 14 (Perica et al. 2018)), and the analyses assume that the annual maximum time series are stationary over the period of record (Perica et al. 2018). This is problematic for flood risk management since small changes in the upper tails of extreme precipitation distributions can have disproportionate impacts on the spatial extent of floodplains, especially in extremely flat or low-lying watersheds like those in southeast Texas.

In this paper, we apply a moving window approach to analyze the spatial and temporal trends in extreme precipitation in southeast Texas. We collect daily total rainfall at more than 600 rain gauges in coastal Texas and Louisiana and use a statistical approach for peaks-over-threshold modeling that employs a generalized Pareto distribution (GPD). We compare the results using our approach to the generalized extreme value (GEV) for estimates using annual, quarterly, and monthly block maxima. Further, we analyze the long-record gauge data in 40-year time windows to evaluate shifts in distribution parameters and extreme precipitation through time at gauge stations where record lengths exceed 80 years and have good fits to the GPD. Spatial analysis highlights significant positive trend in extreme precipitation at several gauge stations in the greater Houston region. As a further exploration into the Houston region, we analyze return level estimates for the watersheds within Harris County. Focusing on these extreme precipitation estimates at the watershed scale can have a more direct affect on the mapping of floodplains in the area.

The results of this study have important implications for flood hazard mapping in the greater Houston region and subsequent flood risk reduction analyses, as well as basic design criteria for a wide variety of hydraulic structures such as culverts, roadway drainage, bridges and small dams. This paper also complements recent literature focused on attributing flood risk in Southeast Texas and coastal Louisiana to climate change and urbanization (Risser and Wehner 2017; Van der Wiel et al. 2017; Van Oldenborgh et al. 2017; Wang et al. 2018; Zhang et al. 2018; Sebastian et al. 2019) and is timely in light of recently released NOAA Atlas 14 results for the State of Texas. In the following section we provide background on relevant literature and describe the study area, followed by an overview of the methods and the results. The paper concludes with a discussion of the major findings and their policy implications, and recommendations for future work.

2 Background

Historically, design rainfall utilized to quantify the SFHA has been developed through the use of an annual block maxima approach that selects the largest rain event per year from local rain gauges and employs the generalized extreme value (GEV) distribution to fit the data and estimate the 1% precipitation level. In extreme value theory, the cumulative distribution function (CDF) of the maximum of a series of independent occurrences can be modeled as a GEV distribution. Typically, this is taken as the maximum occurrence within a block of one year. Then the yearly maxima, x, converge to the GEV distribution of the form:

$$\begin{aligned} G(x)= & {} P(X\le x) = \exp \Bigg (-\left[ 1+\xi \left( \frac{x-\mu }{\sigma }\right) \right] ^{-1/\xi }\Bigg ), \quad \sigma >0, \;\;\xi \ne 0 \end{aligned}$$
(1)

where \(\mu \) is a location parameter, \(\sigma \) is a scale parameter, and \(\xi \) is a shape parameter. The values of these parameters affect the distribution just as their names suggest. The location parameter shifts where the distribution is centered. The scale parameter stretches the distribution, i.e., scales it up or down. The shape parameter determines the shape of the distribution, such as if it is symmetric or skewed one way or another.

Although a large number of studies have implemented this GEV approach for rainfall frequency estimation (Bonaccorso et al. 2005; Yilmaz and Perera 2014; Blanchet et al. 2016; Agilan and Umamahesh 2017; Yilmaz et al. 2017), this methodology may fail to consider valuable precipitation data if two or more large rain events occur in a single year. Consequently, the peaks-over-threshold approach, which selects all occurrences above a certain threshold, may allow for more accurate return period estimation by incorporating a greater number of rain events. Instead of considering the maximum among a series of occurrences (as in the block maxima approach), initially consider all independent rainfall occurrences as identically distributed random variables. In order to analyze the extremes of this series of occurrences, select observations above a certain threshold, u. Then the conditional distribution of these occurrences takes the form:

$$\begin{aligned} P(X>u+y|X>u)= & {} \frac{1-F(u+y)}{1-F(u)}, \quad y>0 \end{aligned}$$
(2)

According to extreme value theory (Coles et al. 2001), for large enough threshold values (u), the conditional distribution converges to the generalized Pareto distribution (GPD) of the form:

$$\begin{aligned} P(X>x|X>u)= & {} \Bigg [1+\frac{\xi (x-u)}{\widetilde{\sigma }}\Bigg ]^{-1/\xi }, \quad x>u \end{aligned}$$
(3)

where \(\xi \) is the same shape parameter as the GEV estimate, and the scale parameter \(\widetilde{\sigma }\) is a function of GEV parameters and the threshold \(\big (\widetilde{\sigma } = \sigma + \xi (u-\mu )\big )\).

Due to its ability to capture a larger amount of data, as well as its theoretical connection to the GEV distribution, the peaks-over-threshold approach has been widely implemented in recent extreme rainfall analyses (Beguería and Vicente-Serrano 2006; Agilan and Umamahesh 2015; Trepanier and Tucker 2018). More recently, studies have implemented modifications to the peaks-over-threshold model that allow for less parameter tuning or allow for consideration of non-stationarity. For example, Naveau et al. (2016) propose an extended GPD model which allows the user to not have to select a threshold. Another uses a log-histospline approach to look at the full range of data as opposed to just the upper tail (Huang et al. 2019). We find these models do not fit our data as well or their methods are too complicated for the goals of this analysis. Other studies have allowed for non-stationary analysis by allowing the scale parameter to change based on relevant covariates (Agilan and Umamahesh 2015). However, identifying appropriate covariates and determining the relationship between each covariate and the scale parameter can be challenging. In order to take into account non-stationarity in the data, we implement a moving window approach. This allows trends in distribution parameters and estimated rainfall quantiles to be observed without pre-specifying external covariates. Additionally, this method allows for all three parameters to shift between windows, rather than only considering changes in the scale parameter. The resulting trends in estimated rainfall can also be calculated separately for each location and then compared to other locations to see how trends vary geographically.

Numerous publications have analyzed changes in the magnitudes of extreme precipitation events for the continental U.S. (Karl and Knight 1998; Groisman et al. 2001; DeGaetano 2009; Pryor et al. 2009; Higgins and Kousky 2013). Several studies have also analyzed trends in the magnitude of extreme precipitation events for the southeastern U.S. (Keim 1997, 1999; Powell and Keim 2015), whereas others have focused specifically on rainfall generated by tropical cyclones (Dhakal and Tharu 2018; Trepanier and Tucker 2018). For example, Trepanier and Tucker (2018) used extreme value statistics to determine that the uppermost tropical cyclone rainfall amounts in the distribution were increasing with time or equivalently, that the most extreme events are occurring more frequently. Dhakal and Tharu (2018) also found evidence to support the idea that heavy rainfall has become more extreme in recent years; however this analysis used the GEV distribution with annual maxima series.

We seek to explore how extreme daily rainfall has changed over time in the southeast Texas region using a combination of GPD peaks-over-threshold modeling and our moving window approach. The GPD has added value over the GEV approach due to the fact that it uses more data (Coles and Powell 1996). Also, as extreme events become more extreme, it is also possible that extreme events are occurring more frequently, and the GPD allows us to include information from more than one event per year. We outline these methods and their details in the following section.

3 Data and methods

3.1 Data collection and processing

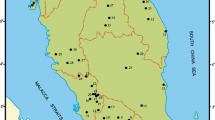
Historical precipitation observations are collected using NOAA’s Global Historical Climatology Network (GHCN)-Daily product version 3.22 (Menne et al. 2012, 2018). GHCN-Daily is a global database of daily observations from land surface stations. Data are quality assured and assembled from numerous sources, including National Meterological and Hydrological Centers (NMHCs) around the world. The period of record at individual stations ranges from less than one year to more than 175 years. For the purposes of our analysis, we have defined the study area as the region encompassed by a rectangle ranging from approximately 28.1–31.0\(^\circ \)N, 92.7–97.0\(^\circ \)W as shown in Fig. 1. In this region, we identified 601 stations for the period between January 1, 1900 and December 31, 2017. We formatted a clean data set that includes daily precipitation totals for only these 601 stations for the time period stated above. This data set can be found at doi.org/10.25612/837.XVGJ30NMA45X [United States National Oceanic And Atmospheric Administration et al. 2020]. Despite considering the period ranging from 1900 through 2017, we note that not all stations provided data for the entire period. This is due to different start and end dates of data collection for each gauge location. The length of available data at each station is indicated in Fig. 1. Due to these varying lengths, not all stations are included in the following analyses. Selection criteria are described in the relevant sections (see, e.g., Sect. 3.4).

Fig. 1
figure 1

Map of study area ranging from approximately 28.1–31.0\(^\circ \)N, 92.7–97.0\(^\circ \)W. The length of data available (in years) at each station is indicated by the size and color of the point. The red star in the inset map indicates where this region is located within the United States

Full size image

After the initial data collection, the rainfall time series are processed in order to facilitate the selection of independent rainfall events. Since the extreme value theory adopted in this analysis assumes each occurrence is independent, we need to pre-process our data so that occurrences are not correlated with each other. Correlation between occurrences could result from a single storm event that produces multi-day precipitation and more than one of the days exceeds the specified threshold u. In this case, although the threshold was exceeded twice, there was actually only one storm occurrence, so only the highest daily total should be selected. Modifying the data to select only independent events is known as declustering, and has been widely implemented in rainfall time series analyses (Coles et al. 2001; Agilan and Umamahesh 2015; Gilleland and Katz 2016).

Declustering is achieved by examining the autocorrelation at several representative rain gauges (the top five gauges with the longest records). Across these gauges there was a sharp decline in correlation at time lags of one day or greater. Thus, the time series of each rain gauge is processed so that only the highest rainfall day is selected if there are multiple days of consecutive rainfall, and rainfall occurrences must be separated by at least one day of zero rainfall. More simply, if there are two or more consecutive days of nonzero rainfall, the maximum day remains and the other days are set to zero. After this declustering process, the data are now considered independent so that they can be used for the following peaks-over-threshold method.

3.2 Peaks-over-threshold modeling

For our analysis, we use a peaks-over-threshold modeling approach in combination with the GPD. We first select a common threshold, then utilize it to fit threshold excesses from each station to a GPD. We assess the ability of the fitted GPD to represent the data by performing a goodness-of-fit test using the Cramér-von Mises (CVM) statistic. This test compares the empirical distribution function of the data to the CDF of the GPD. We use a p value cutoff of greater than 0.01 for the test to determine a good fit. The R package gnFit is used to calculate this statistic (Saeb 2018).

3.2.1 Threshold selection

In order to use the peaks-over-threshold modeling approach, we must first select a threshold. The traditional method of threshold selection is used, utilizing mean excess plots and parameter stability plots (Coles et al. 2001; Beguería and Vicente-Serrano 2006). For each of these plots, the x-axis is a changing threshold. The model is fit using that threshold and mean excess and parameter values are calculated from this fit. Mean excess values are just as their name suggests—average (mean) excesses over the threshold, or the average of the values which exceed the given threshold. The parameter values are simply the estimated parameters for the fit of the data for a specified threshold. Parameters include the shape (\(\xi \)) and scale (\(\sigma \)). Within the mean excess plots, we look for a threshold value where the plot has a linear trend to indicate a good fit to the GPD. For the parameter stability plots, we look for a threshold value around which the parameter value is stable, i.e., where we see a horizontal line in the plot as the parameter value is constant across similar threshold values.

In order to select a common threshold across all stations in our data, we select ten representative stations which are spaced approximately evenly throughout the study region. Each chosen station has a long period of record, ranging from 57 to 117 years. Using the methods described above on the full data history of each of the ten stations, we determine a range of possible thresholds for each station. An example mean excess plot for one of these stations can be seen in Fig. 2. Comparing the findings for all ten stations, we discover a common threshold which falls within each station’s range. We choose this common threshold as 25.4 mm (1 inch) for the 24-h rainfall.

Fig. 2
figure 2

An example mean excess plot for one of the ten representative stations. The chosen threshold of 25.4 mm is marked with the blue dashed line

Full size image

3.2.2 Return levels

In this study, our main interest lies in calculating rainfall return levels. Return levels are extreme rainfall statistics, and are used to associate a specific duration of rainfall with a given time period. For example, a common duration of interest is daily or 24-h rainfall. However, other durations such as 1-h, 12-h, 2-day, or 3-day can also be used to assess flood hazards. An N-year return level is defined as the amount of rainfall expected to be met or exceeded on average once every N years, where this N years is called the return period. Equivalently, this is the amount of rainfall that has a \(\frac{1}{N}\) probability (or \(\frac{1}{N} * 100\) % chance) of being met or exceeded in any given year. Consequently, return levels are also commonly referred to as X% precipitation events, where X \(=\left( \frac{1}{N} * 100\right) \). For example, an event with a 100-year return period is equivalent to a 1% precipitation event. Herein, we will use this return level notation over that of the X% precipitation event. An N-year return level is also contingent on the time duration of analysis, i.e., one would expect a 100-year 24-h rainfall to be larger than a 100-year 12-h rainfall at a given location.

Return levels for each station can be calculated directly from the fitted distribution parameters (\(\sigma , \xi \), and threshold u) obtained during the peaks-over-threshold modeling, along with some information about the data and its rate of exceedance. We calculate our return levels and corresponding confidence intervals using the R package extRemes (Gilleland and Katz 2016). This method is the same as that of Bommier (2014), where the equation for an N-year return level, \(x_N\), is:

$$\begin{aligned} x_N= & {} {\left\{ \begin{array}{ll} u + \frac{\sigma }{\xi } \left[ (\lambda N)^\xi -1\right] &{} \text {if } \xi \ne 0 \\ u + \sigma \, log(\lambda N) &{} \text {if } \xi = 0 \end{array}\right. } \end{aligned}$$
(4)

with \(\lambda = \frac{n_u}{M}\), where \(n_u\) is the number of exceedances observed over the threshold (u), and M is the number of years in the period of observation. \(n_u\) and M will vary greatly by station.

3.3 Time series representation: moving windows

To answer the question of whether extreme rainfall statistics have changed over time, we construct time series for each station out of the data ranging from 1900 to 2017. Data are grouped into moving time windows. The window remains constant in length across time. We choose for the length of our window to be 40 years. This length is chosen from a mixture of hydrological knowledge and statistical testing. First, we acknowledge that the length of the window must be long enough so that natural variability in wet and dry seasons will not drive our variability from one window to the next (i.e., the window must be wide enough so that the average climate values over the period will be considered stable). It is commonly designated that at least a 30-year long window is necessary to do this (Guttman 1989), or more specifically a “relatively long period comprising at least three consecutive ten-year periods” (World Meteorological Organization 1984). Therefore, window lengths of 30, 40, and 50 years are tested. After examining the plots of the time series created by these moving windows for our longest stations, it is found that the 40-year time window provides a good balance between variability and smoothness in the resulting time series.

Therefore, for our analysis data are grouped into 40-year time windows. That is, for the first 40-year window for a specific station we subset the data to the range January 1, 1900 to December 31, 1939, fit a GPD with the specified threshold, and save the parameter estimates. This process is repeated for each 40-year window, where it is incremented by one year each time. Consequently, the second window ranges from January 1, 1901 to December 31, 1940. This continues until the final window ranges from January 1, 1978 to December 31, 2017. This moving window approach enables us to observe how the distribution parameters change for each station over time, as well as the return levels.

While observing these trends over time is interesting on its own, it is illustrative to put these trends into context of geography. We bring in the spatial aspect by finding which stations have a significant increasing or decreasing trend, as well as where they fall on a map. These comparisons can be seen later in Figs. 5 and 6, respectively. In addition to comparison of trends, we focus on results from the last 40-year window in order to compare recent return level estimates for each watershed to the current standards.

3.4 Return levels by watershed

Looking particularly at the most recent 40-year period, which includes Hurricane Harvey, we compare these return levels to the Harris County Flood Control District (HCFCD) standards last updated in 2009 and used to map floodplains in Harris County. We organize the stations by watershed within Harris County. HCFCD watershed boundaries are approximately equivalent to the HUC10 watersheds delineated by the USGS. Since we have a limited number of stations, not every watershed is represented. A map of the Harris County watersheds together with their alpha code is shown in Fig. 3.

Fig. 3
figure 3

Map of watersheds in Harris County, adapted from a similar map from the HCFCD Hydrology and Hydraulics Guidance Manual (Storey and Talbott 2009). Each color corresponds to a different watershed, which is labeled both by its name and a letter. These letters, which are defined by the HCFCD Unit Numbering System, correspond to the given watersheds. The map includes a representation of which hydrologic region each watershed falls within, shown by the color of its boundary. (Table 3 also summarizes this information.) The plot also shows the locations of the 38 stations used in our watershed analysis in Sect. 4.3, illustrated by the black dots

Full size image

The return levels reported for HCFCD are not displayed by station or watershed, but rather by groups of watersheds, called hydrologic regions. “Three hydrologic regions [in Harris County] have been established to more accurately define rainfall parameters” (Storey and Talbott 2009). Table 3 illustrates which watersheds are included within each hydrologic region. We compare each station’s calculated return level for the last 40 years (1978–2017) to the level reported for the hydrologic region corresponding to their respective watershed. Some stations are not included in this analysis due to short period lengths (< 5 years) or poor fit to the GPD (Cramér-von Mises goodness-of-fit p value \(\le \) 0.01). These are not included since Eq. (4) depends on the number of years in the period of observation, and short period lengths correspond to irrationally large return levels. Overall, 38 stations are used for this analysis. Their locations are mapped in Fig. 3.

3.4.1 Weighting methods

While removing stations with unreasonable estimates helps to create a more accurate mean return level per watershed, there are still stations included with only 5 or 6 years worth of data, which will result in estimates with high standard errors (high uncertainty or variation). In order to account for this uncertainty, each return level estimate is weighted by its inverse standard error, standardized across those within the same watershed (i.e., the weights for all stations included within one watershed will add up to one). This method results in larger weights for more accurate estimates and smaller weights for those with large variation. The mean for each watershed is calculated as a weighted average using these weights. These weighted means are then compared to the standards given for the hydrologic region.

The equations used to calculate the weighted mean are included below. Note that the weighted mean \(\, m_w \,\) is calculated separately for each watershed, where the watershed includes the stations \(i = 1, \ldots , k\)

$$\begin{aligned} m_w= & {} \frac{\sum _{i=1}^k x_{N_i} \;w_i}{\sum _{i=1}^k w_i} \end{aligned}$$
(5)
$$\begin{aligned} w_i= & {} \frac{SE_i\,^{-1}}{\sum _{j=1}^k SE_j\,^{-1}} \end{aligned}$$
(6)

where \(\; x_{N_i} \;\) and \(\; SE_i\,^{-1} \;\) are the return level estimate for station i and the inverse standard error of that estimate, respectively. The weights \(\, w_i \,\) are calculated for each station i within a watershed, where the watershed includes stations \(j = 1, \ldots , k\). It can be noted that \(\sum _{i=1}^k w_i = 1\).

In our exploration of the data, those stations with a small number of years correlated to a larger standard error, and therefore smaller inverse standard error. Therefore, this weighting based on the standard errors helps to account for the uncertainty caused by varying station lengths. Comparison of the weighted means to the current standards is described in Sect. 4.3.

4 Results

4.1 Comparison of methods

Since our motivation behind pursuing a peaks-over-threshold approach is to include more than one extreme event per year, we compare our GPD peaks-over-threshold approach (see Sect. 3.2) to not only the GEV fit on annual maxima, but also on quarterly and monthly maxima. Extending the GEV to include four or twelve maxima per year can help alleviate some of our concerns for there being more than one extreme event per year; however we still prefer the GPD approach so there is not a defined number of events we are including. For the GPD case, this number is instead determined by how many days had rainfall above a certain threshold. We provide comparison of these method results below.

As explained in Sect. 3.2.2, we will focus on rainfall return levels determined by a model’s fit. Table 1 displays the 100-year return level and 95% confidence bounds produced by each fitted model. This analysis is conducted on the full history of the Houston Hobby Airport station, and the threshold used for the GPD fit is our chosen 25.4 mm (1 inch). The selection of Hobby for this example is due to its long period of record (about 87 years), its central location in Houston, and its use in other literature on the Houston area (Huang et al. 2019). The results indicate that the GPD provides higher estimates of return period rainfall than either the GEV annual or quarterly max (Table 1). However, the GPD yields a lower estimate than the GEV monthly max. This might be due to overfitting for the GEV monthly max, since it may be that not every month has an extreme event. Note also that the width of the confidence intervals are similar (around 153 mm) for the GPD, quarterly max, and monthly max, while the width for the annual max is much wider (almost 200 mm). This indicates that the GPD may provide similar results to the GEV quarterly or monthly max, but is definitely preferable over the GEV annual max. Overall, using the GPD provides a good balance and allows us more flexibility, as we do not have to determine whether it is best to include four or twelve maxima per year.

Table 1 Comparison of 100-year return levels and 95% confidence bounds (given in parentheses) for the models fit to the full history of Houston Hobby Airport. Return levels are stated in mm
Full size table

4.2 Trend analysis

From our generated time series from the moving windows, we are able to plot the trends of return levels over time for each station. It is difficult to see if this trend is overall increasing when looking at all of the 601 stations, as not all of the stations cover the entire study period. In fact, many station lengths are only a few years long. If we limit our analysis of the trends to those stations that had at least 80 years of data and a good model fit to each window and the full station length, we glean a better understanding of the true trends. We define a good model fit to be that where the Cramér-von Mises goodness-of-fit p value is greater than 0.01.

We begin our trend analysis by observing the time series of return levels created using the moving-window approach. First, we examine the trend of a single gauge location, focusing again on the Houston Hobby Airport station. Plots of Hobby’s modeled return levels over time can be seen in Fig. 4a. Evident in this figure is the pattern that the 500-year return level changes more dramatically than the 100-year, i.e., has a steeper slope to its simple regression line. The same relationship appears between that of the 100-year and 25-year, though not as extreme.

Fig. 4
figure 4

a Return levels for Hobby Airport station as modeled over time in 40-year windows. Each point corresponds to a return level calculated from the GPD fit for that 40 years, where the point is labeled on the x-axis by the ending year of that 40-year window. A simple regression line is fit to each of the trend lines for the 25-, 100-, and 500-year return levels to display the overall increasing trend for each. b 100-year return levels for Hobby Airport station as modeled over time in 40-year windows. The 95% confidence intervals for these estimates are also included

Full size image
Fig. 5
figure 5

Modeled 100-Year return level trends for all stations with at least 80 years worth of data and a good model fit to each window and the full station length. This plot compares the trends of stations found to have a positive slope (in blue), a negative slope (in red), or no significant slope (in black). The bolded blue line is the Houston Hobby Airport station

Full size image

Although we can observe these time series at each station to determine how return levels have changed over time, some do not have as visible of a trend as at the Hobby station. The trend lines for the modeled 100-year return levels for all stations considered are shown in Fig. 5. In order to determine if the overall trend is increasing or decreasing, a trend test is run on each station’s time series. At first, we ran a Sen’s slope test and found many stations to have significant positive or negative slope. A slope is defined as significant if the slope coefficient had a p value less than or equal to 0.05. However, since our 40-year windows overlap with each other, there is autocorrelation between our return level estimates from one year to the next. In order to account for this autocorrelation in our estimate of the slope (i.e., the change in 100-year return level in mm/year), we instead fit the data to a linear regression with autocorrelated errors. Specifically, the errors are modeled as an AR(1) process using the astsa::sarima function in R (Stoffer 2019). Stations were found to either have a significant positive slope, significant negative slope, or slope not significantly different from 0. The results are shown in Table 2 and the corresponding station locations are plotted in Fig. 6.

Fig. 6
figure 6

Map of the stations that are included in Fig. 5, where the color and size of the points indicates the slope resulting from a linear regression with autocorrelated errors fit on the trend-over-time lines. If the test indicates a significant slope, the station is colored as blue for a positive slope value and red for a negative slope value. If the test indicates a slope not significantly different from 0, the station is colored as black. The points are sized by the absolute value of the slope and concentric circles are used to denote the relative slopes of the 25-, 100- and 500-year trend lines, where the outermost ring represents the slope of the 500-year and the size of the smallest filled circle indicates the slope of the 25-year return levels

Full size image
Table 2 Slope estimates for the 25-, 100-, and 500-year return levels at the stations that are included in Figs. 5 and 6. The 95% confidence bounds are given in parentheses. Stations are colored by slope in blue, red, or black, just as they are in Figs. 5 and 6
Full size table

Of the 18 stations with record lengths equal to or exceeding 80 years and with good fits to the GPD, seven stations have experienced significant changes in extreme rainfall. Five stations (455, 470, 548, 574, and 578) have experienced statistically significant increases in extreme precipitation, where the rate of change for the 500-year exceeds the rate of change for the 100-year which, in turn, also exceeds the rate of change for the 25-year. This is consistent with the pattern shown in Fig. 4a for Hobby Airport. The greatest positive rate of change in extreme rainfall is observed at Station 470 (near Danevang, TX) where the 500-year return period event has increased by approximately 3.76 mm/year over the period of record. Decreases in extreme rainfall are also observed at two stations: 556 and 591. The largest absolute change in extreme precipitation is observed at station 591 (near Galveston, TX) where the 500-year return period event has decreased by approximately 7.76 mm/year over the period of record. Significant downward trends, while smaller, are also observed at this gauge for the 25- and 100-year return levels.

4.3 Return levels by watershed

Mean return levels for each watershed are determined through the method described in Sect. 3.4.1. Recall from Sect. 3.4 that only those stations with at least five years of data and a good fit to the GPD for the most recent 40-year period are included. This leaves the 38 stations that are plotted in Fig. 3 and listed in Table 4. Note that some of the stations are not visible on the plot in Figs. 7 and 8, but are still included in the calculation for the mean. The cutoff used for plotting is an inverse standard error of \(\ge \) 0.0025, which corresponds to those stations with a return level estimate of \(\le \) 600 mm. The return levels and standard errors for each of the 38 stations are given in Table 4 in the “Appendix”. Figure 7 shows the return levels and weighted means at each station. The size of the dots reflect the inverse standard error of the return level estimate, i.e., the larger the dot, the smaller the standard error, and the more certain the estimate. The mean for each watershed is also calculated as a weighted average using the weights from Eq. (6). These weighted means by watershed more accurately reflect return levels by including information on the uncertainty in their estimates. These results can be compared to the unweighted means in Fig. 8 in the “Appendix”. Return level means for each watershed are found to be much higher when all stations are weighted the same, as this allows high, uncertain estimates to have a larger impact on the mean. These differences demonstrate the importance of taking the uncertainty of estimates into account.

Fig. 7
figure 7

100-Year return level estimates for 1-day rainfall given the last 40 years of data. Each dot corresponds to one station falling within Harris County. The size of the dot corresponds to the inverse standard error (SE) of that station’s return level estimate. Stations are sorted by watershed, which are stated on the y-axis. The watersheds are also grouped into their hydrologic regions, separated by the dashed lines. The blue stars represent the weighted mean return level across stations within a watershed. Here the weighted mean for each watershed is based off of inverse standard error weights. The purple lines correspond to the 100-year return levels reported for the hydrologic regions by HCFCD (Storey and Talbott 2009). Note that the blue stars for Addicks Reservoir and Sims Bayou fall directly on top of a dot because there is only one station included within each of these watersheds

Full size image

5 Discussion

Recall that our modeling is based on fitting data of excesses over a fixed threshold using the GPD. This method differs from that used by previous studies to determine benchmark precipitation events necessary to set floodplains. These studies have used the GEV distribution fit to annual maxima. However, for these larger studies, they often have access to more data—to stations with longer or more complete histories. Since we are working with less data, and are particularly interested in 40-year windows, the GPD provides us with a more flexible option to calculate return levels given less data.

Through our trend analysis based on the moving-window approach, we are able to identify stations which exhibit a significant increase or decrease in return level estimates over time. These results differ from other studies because they have different modeling approaches or focus solely on tropical cyclones; however they provide similar results that heavy rainfall is becoming more extreme in Houston and the southeastern United States (Dhakal and Tharu 2018; Trepanier and Tucker 2018). These trend results have not been discovered in the more official literature due to the different questions they are trying to answer, and so they focus on fitting all of the available data at once (Asquith 1998; Perica et al. 2018). These studies also assume stationarity of the data. Meanwhile, we focus on directly modeling the nonstationarity of the data and observing its trend over time. This is because we are primarily interested in the temporal patterns in the data. We summarize this data into a slope estimate, i.e., how the return levels have changed in mm/year. When comparing the slopes between the 25-, 100-, and 500-year return level series, it is evident that the slope increases in absolute value as the return period increases. This indicates that rainfall extremes are becoming more extreme, and moreso for those with larger return periods. This finding is consistent with previous studies when looking at extreme rainfall (Dhakal and Tharu 2018; Trepanier and Tucker 2018).

In addition to observing temporal patterns, we also view these trends spatially by plotting the trend slopes in relation to where the stations fall on a map. We observe a fairly strong negative trend for station 591 near Galveston, TX. Upon closer inspection, we discover that despite having long histories of data, both stations with a negative trend (591 near Galveston, TX and 556 near Sealy, TX) are missing data for recent years, including 2017. This missing time period includes many high rain events which may impact the trend assessment. Please see Sect. A.2 in the “Appendix” for the details of our explorations into these stations.

Observing how these trends differ across locations raises two important questions. What is causing these trends and why do they differ over space? A possible cause for changing extreme rainfall is climate warming. Several studies performed after Hurricane Harvey in Houston found that climate warming increased the probability of Harvey-level rainfall (Emanuel 2017; Risser and Wehner 2017; Wang et al. 2018). Wang et al. (2018) uses atmospheric modeling to demonstrate that climate warming over the late 20th century contributed up to 20% of the increases in extreme precipitation in Texas. These studies suggest that trends observed in our analysis may be due to incremental climate change. In addition to observing how trends change over time, we are also interested in how these trends vary over space. Trepanier and Tucker (2018) highlight the geographic variability of risk and how extreme rainfall can differ from one location to another. An analysis into changing extreme rainfall of the southeastern United States says that “slopes along the coastal sites are higher in magnitude as compared to the inland areas” (Dhakal and Tharu 2018), suggesting that patterns along the coast may differ from those inland. Another variable that can affect the extreme rainfall at a certain location is the amount of urbanization in the area. Recent research has highlighted the role of urban growth in exacerbating rainfall totals. For example, Zhang et al. (2018) demonstrated that urbanization in the Houston region increased the probability of Hurricane Harvey’s total rainfall by over 21 times. This indicates to us that the spatial differences in trend found in our analysis could possibly be attributed to the varying levels of urbanization in Houston as compared to the surrounding area.

From our analysis of return levels by watershed, we find that a majority of our mean return level estimates exceeded those of the current standards (see Fig. 7). Through our analyses, it is clear that extreme rainfall has changed over time in some areas. Due to these changes, it is important that we update our extreme rainfall estimates more often. The HCFCD standards we compared to were last evaluated in 2009 (Storey and Talbott 2009). NOAA Atlas 14 recently came out with updated rainfall estimates for all of Texas in 2018 (Perica et al. 2018). Before this, the last time rainfall frequency estimates had been calculated for all of Texas was in 1998 (Asquith 1998), and before that was in the 1960s and 1970s (Hershfield 1961; Frederick et al. 1977). NOAA Atlas 14 also found increased return levels in the Houston region (Perica et al. 2018) compared to their previous evaluation of 24-h precipitation (Hershfield 1961), further supporting the idea that these estimates need to be evaluated more often, especially in more urban areas.

6 Conclusions

The focus of this paper is a refinement of our understanding of changing rainfall patterns for the greater Houston region. To meet this objective, we applied a moving-window approach to analyze the spatial and temporal trends in extreme precipitation in Southeast Texas. We collected daily total rainfall at more than 600 rain gauges in coastal Texas and Louisiana. At stations with records equal to or exceeding 80 years (i.e., 18 stations), we fit the GPD to 40-year time windows and evaluated shifts in distribution parameters and extreme precipitation through time. We found statistically significant trends in extreme precipitation at several gauges in the region, mostly in the urban area of Houston. At all stations we find that the rate of change (positive or negative) is larger for less frequent events—or, equivalently, we find that extreme events are becoming more extreme. This is in line with findings from other studies in the region (Trepanier and Tucker 2018) and in the southeastern U.S. (Dhakal and Tharu 2018). When comparing the results for the 1% return frequency events, we show that our analysis using only the last 40 years of data generally provides higher values than those currently used to map floodplains at watersheds in Harris County. The latter values were derived using annual maxima and assume stationarity leading to a mischaracterization of extreme rainfall over the most recent period of record. This finding is important because small changes in the upper tails of extreme precipitation distributions can have significant impacts on the spatial extent of floodplains, especially in extremely flat or low-lying areas like the Texas Gulf Coast. Our methodology produces improved estimates of the average return level within each watershed of the region. These estimates have significant consequences for both the standards set for infrastructure design and building codes which are important for flood resilience of the region.

While this study takes important steps towards understanding temporal trends in extreme precipitation and their spatial distribution, in the greater Houston region, further research is needed. First, we only considered trends in 24-h precipitation totals; however, urban flooding is also driven by shorter, more intense precipitation events. Further research is needed to better understand whether there have been significant changes in sub-daily precipitation depth or temporal distribution, and how such changes impact the design of engineering infrastructure (e.g., stormwater networks). Second, this study does not consider spatial dependency between gauge observations. Future work should examine spatial variability in precipitation extremes over a larger study region. Third, additional work is needed to identify potential underlying variables that might be influencing spatiotemporal variability in precipitation, such as climate change and urbanization. Visualizing patterns in precipitation extremes would shed light on the importance of landscape and development features on precipitation. Fourth, future research should isolate different types of precipitation events, such as those driven by mesoscale convective systems (MCSs) or tropical cyclones, to better understand variability due to weather patterns. Finally, more work should be done to quantify how flood risk has changed over time due to changing precipitation patterns. For example, studies which map changes in flood hazards and exposure are especially important for establishing the economic costs associated with changing precipitation patterns and critical for decision makers interested in facilitating community resilience to future floods.