An evaluation of the performance of rock fall protection measures and their role in hazard zoning

Abstract

Rock falls threaten human lives and assets in mountainous regions all over the world. Protection measures are one of the most effective solutions for mitigating rock fall-related hazards and risks; however, their optimal working conditions must be ensured throughout their whole life span, in order for the measures to play their role properly and not to have their performance compromised. This paper presents a methodology for a simple yet effective evaluation of the performance of existing rock fall protections, whose goal is to establish their actual performance capacity and, based on that, whether they can play their mitigation role. The methodology is articulated into four main steps. In the first, data and information about the hazard affecting a site, the current state of existing protections and possible faults/causes of malfunctioning of the protections are collected. The second and third steps evaluate the actual performance capacity of the protections in comparison with their nominal capacity, after the potential influence of the factors degrading the effectiveness, detected in the first step, is considered (i.e. factors reflecting negative interaction between site and measures, structural design issues of the protections, faults and malfunctioning due to lack of maintenance, etc.). These three steps were implemented in a spreadsheet tool, allowing to store relevant data on protection measures collected during a field survey and to perform the evaluation analysis directly on site, semi-automatically, based on the data collected. Finally, once an actual performance capacity is obtained from these evaluations, the last step of the methodology is to compare this capacity to the hazard at the site, in terms of energy and return period of the events at each location of interest, to establish whether the protections can in fact mitigate such hazard or need intervention (reparations, replacement, etc.). A detailed application of the whole procedure is shown, by means of a demonstrative example carried out at a Swiss site where rock fall protections measures were previously installed and hazard zoning maps are available.

1 Introduction

The constant growth of urban areas and human activities has led to exploiting lands which, when located in mountainous areas, can be found to be closer and closer to potential landslide-prone slopes. Rock falls, in particular, can constitute a serious threat to human lives and assets in these areas, due to the velocity of the process and associated energy of impact. Ensuring the safety of the areas potentially affected is therefore of paramount importance and many regions and countries concerned have been trying to establish at best measures for hazard and risk management. Both in territories where landslide hazard (and/or risk) management guidelines have been issued (MATE/METL 1999; Interreg IIc 2001; AGS 2002; Lateltin et al. 2005; Copons et al. 2001; Corominas et al. 2003) and in those cases where a general framework is missing and rock fall hazards are dealt with in the context of specific case studies (Topal et al. 2007; Agliardi et al. 2009), rock fall protection measures constitute an important solution for mitigating potential consequences.

Several types of solutions exist in terms of protections, as well as some guidelines for their proper design (Volkwein et al. 2005; Muhuntham et al. 2005) and strategies of implementation (Volkwein et al. 2011; CCC 2013). Under the condition of an appropriate design, constructive measures such as barrier fences, dams, ditches, anchors/bolts and wire mesh cable nets on rock walls (to name the most common types) can be used very effectively to reduce rock fall risks to negligible (or at least acceptable) levels.

Needless to say, as any other engineering work, all types of protection measures are conceived to operate within a characteristic life span, therefore maintenance can be as essential as the correct design of the structural measure itself, in order to guarantee an optimal performance throughout the years (Keusen et al. 2008; Volkwein et al. 2011; Prina Howald et al. 2017).

If this point might at first seem obvious, in reality it is often times not guaranteed: for example, the nets of barrier fences can be partially filled by blocks and/or other materials, rock blocks can cumulate behind protective dams or inside ditches, mesh wire cables or the nets of barrier fences can have undergone some deformation (which can happen also to any ductile element of any type of protection), any metal part of a given type of protection can be affected by corrosion, etc.

Issues such as those mentioned above negatively influence the operation of a protection measure, up to the point of compromising it. This eventuality suggests that potential rock fall risks at a given site should be evaluated as a function of the actual state of the protection measures. For instance, when the state is such that only some ordinary maintenance is required to restore its full capabilities, the protection can be considered able to play the mitigation role it was designed for. On the other hand, if no maintenance solution would be sufficient to solve the issues affecting the protection, the current condition might demand to ignore its presence and, rather, replace it.

In the framework of landslide risk management (Fell et al. 2005), the problems just introduced might not only have direct consequences at the rock fall risk mitigation level, i.e. usually the phase where the possibility of protections is considered, but even before, at the hazard analysis stage. Risk analysis is a more complicated task than hazard analysis, because of the several types of risk which can be defined (and therefore assessed), the inherently complex aspect of landslide vulnerability, the estimation of monetary values of assets at risk, if required, etc. It is not surprising therefore that not many risk maps and risk mapping methodologies are available still today, and landslide risk assessment (including zoning) stops more often at the stage of hazard assessment and zoning (MATE/METL 1999; Interreg IIc 2001; AGS 2002; Lateltin et al. 2005; Copons et al. 2001). This is the reason why hazard zoning maps, rather than risk, are sometimes elaborated trying to take also the effects of rock fall hazard mitigation by means of protection measures into account. In these instances, it is consequently very important to assess whether the protection measures can or cannot work properly. If rock fall protections can be ascertained to work as per design, it appears reasonable to show and consider the theoretical effects of their mitigation in hazard zoning. On the contrary, if protections cannot work properly, it would seem correct not to take them into account in the hazard evaluation, as they cannot actually modify it (at least, not as much as desired); accordingly, hazard zoning should be (re-)assessed as if no protection would exist at the site and, as a consequence, associated land use regulations should reflect this situation rather than the one in presence of protections.

At present, not many recommendations and/or approaches exist for evaluating potential rock fall protections malfunctioning and their consequences on the hazard affecting a given site (Keusen et al. 2008; Grisanti and Prina Howald 2015; Prina Howald et al. 2017; Abbruzzese and Prina Howald 2018). Yet, the problem is relevant, as land use decisions might depend on the performance of the measures, according to the degree of hazard and risk mitigation provided.

The work presented in this paper shows an application of the methodology introduced in Prina Howald et al. (2017) and Abbruzzese and Prina Howald (2018), for evaluating the performance of existing rock fall protection measures and define their role in rock fall hazard zoning. The approach was developed at the Institute of territorial engineering (Insit) of the School of Management and Engineering Vaud (HEIG-VD), University of Applied Sciences and Arts Western Switzerland (HES-SO). At first, the main features of the methodology detailed in Prina Howald et al. (2017) are recalled; then an example of evaluation of the performance of rock fall protection measures and related influence on rock fall hazard zoning is illustrated. The application was carried out at a study site in Switzerland.

2 Methodology

The procedure for determining the effectiveness or rock fall protections (Prina Howald et al. 2017; Abbruzzese and Prina Howald 2018) is based on a simple method, using a heuristic approach. Its goal is to determine how much the performance capacity of a protection measure existing for some years (or even decades) at a given site can be lowered, due to different factors influencing its conditions, in comparison to its fully operational state (i.e. as per design). The idea behind the method can be summed up as follows:

• express the optimal performance of a rock fall protection in quantitative terms (e.g. for a barrier fence, this could be represented by the energy absorption capacity and the probability of a block propagating beyond the barrier);

• consider all (or at least most of) the factors which could influence the correct behaviour of a protection;

• assign to each factor a coefficient accounting for the potential loss of performance due to that factor (loss more or less pronounced, as a function of how serious the effect of this factor is on the protection);

• multiply the parameters quantifying the performance capacity of the protection by the relevant coefficients specific to the problem studied (number and type of coefficients to be used are to be determined case by case) and determine updated values of the performance capacity.

Once the performance capacity of the protections is computed, it is possible to verify whether the protections can play their mitigation role, and the hazard assessment should accordingly take this into account, or, on the contrary, the protections should be ignored due to major problems, i.e. the hazard should be estimated as if they were not present.

2.1 Concept and structure

The methodology aims at evaluating the performance of six main types of rock fall protections, i.e. barrier fences, dams, wire mesh/cable nets, walls, topographic modifications (slope re-profiling) and anchors, and includes the principles and phases of evaluation’ mentioned above into the following four steps (Prina Howald et al. 2017; Abbruzzese and Prina Howald 2018):

• (a) hazard information at the site and data collection about the conditions of the protections;

• (b) analysis of the performance capacity according to a so-called “Scenario 0”;

• (c) analysis of the performance capacity according to so-called “Scenarios 1–6”;

• (d) requalification of the hazard zones (if possible).

• (a) Landslide hazard at a given site must be determined based on the process intensity I and frequency of occurrence f (Fell et al. 2005; Fell et al. 2008). For rock falls, these parameters are usually expressed by energy E and return period T (inverse of a frequency of occurrence f), respectively. Each point of a slope overhung by unstable rocky cliffs, for which hazard assessment and zoning have been performed, can therefore be characterised by a couple (E, T) representing the hazard at that location.

  If protection measures are present in the endangered area, their task is to lower the hazard beyond their location as much as reasonably possible. This means lowering rock fall energy E and frequency of occurrence f, i.e. lower E and increase T (as T = 1/f), to new values (E*, T*). The performance capability of the measures could then be in general expressed in terms of energy retention E_opt and (reduction of) rock fall occurrence T_opt.

  During this first step, the data to be collected about the measures aim at qualifying the measure in terms of (E_opt T_opt) and, at the same time, define which factors affect their behaviour, in order to assign appropriate values to the coefficients introduced above, called “penalty coefficients”, used to model the loss of performance of a protection.

  These coefficients are divided into two main categories, the first (Group 1) focused on environmental factors interacting with the measure and some general engineering design features of rock fall protections, the second (Group 2) concerning potential faults conditioning the operation of the measures under the structural point of view. Their values range from 0 to 1, where 0 means total loss of performance of the protection due to the factor(s) these coefficient(s) represent, while 1 means no effect at all on the protection.

• (b) The analysis of the performance according to Scenario 0 is a first step of performance evaluation based on the use of coefficients of Group1 only. Examples of typical environmental factors considered in this group are: potential frequent presence of snow filling nets of rock fall fences or cumulating behind upslope faces of dams, effects of freezing/thawing on the structures, presence of springs/torrents/rainwater flow around the protections, outcropping rocks located just before, etc. Factors linked to the general engineering design of the measures may on the other hand include: changes in norms of concept and design, manufacturing issues, points of weakness in the structure of the measures, possibility of plastic deformations, etc.

  The effects of these factors on the protection measures can be expressed as:

  $$ E_{\text{eff}} = E_{\text{opt}} *\mathop \prod \limits_{i} e_{0,i} $$

  (1)
  $$ T_{\text{eff}} = T_{\text{opt}} *\mathop \prod \limits_{i} t_{0,i} $$

  (2)

  where E_eff and T_eff express the performance capacity of the protection measure in terms of effective energy retention capacity and return period (inverse of the effective frequency of occurrence) values, respectively, after the reduction of E_opt and T_opt due to the penalty coefficient (e_0,i, t_0,i) for factor i (factors belonging to Group 1). For each factor i, in particular, two penalty coefficients are actually defined, one for the energy retention (e_0,i) and one for the return period (t_0,i) as, in general, a given factor i might not influence the same way both aspects characterising the capabilities of each protection measure. However, this does not exclude that, in some cases and for some factors, E_opt and T_opt could be considered to be affected approximately the same way and, therefore, e_0,i and t_0,i would be assigned the same value.

• (c) The analysis according to Scenarios 1 to 6, on the other hand, represent the second and final step of evaluation of the performance capacity and addresses potential problems to the protections associated to several types of faults/causes of malfunctioning, specified as follows:

• (1) faults of positioning;

• (2) faults in the design of the measure;

• (3) faults of construction/installation;

• (4) lack of maintenance;

• (5) issues due to life span attained;

• (6) issues due to “residual conditions”, i.e. behaviour of the measures beyond life span.

Accordingly, factors belonging to Group 2 are subdivided into 6 sub-groups, one for each type of issue listed. The most frequent problems can be related to lack of maintenance over time (types 4, 5, 6), but some others might also concern the engineering design and construction (e.g. types 2 and 3).

This step (c) of the methodology is conceived and run the same way as step b), but using solely these coefficients:

$$ E_{\text{red}} = E_{eff,o} *\mathop \prod \limits_{k} \mathop \prod \limits_{j} e_{k,j} $$

(3)

$$ T_{\text{red}} = T_{eff,0} *\mathop \prod \limits_{k} \mathop \prod \limits_{j} t_{k,j} $$

(4)

In Eqs. 3 and 4, E_red and T_red are the reduced energy retention capacity and return period values, respectively, obtained from the effective values E_eff and T_eff after the further reduction caused by the application of the penalty coefficients (e_k,i, t_k,j) for each factor j (factors related to the faults in the measures) of each scenario k involved.

(d) The possible requalification of hazard is done based on the results of the previous evaluations. As explained in Prina Howald et al. (2017) and Abbruzzese and Prina Howald (2018), if the protection is effective, i.e. its performance capacity is such that (E_red, T_red) > (E, T), the protection can be assumed to work properly, and most likely only a minor maintenance work is required to restore its operation to optimal. The hazard at the locations beyond the protection measures is therefore mitigated as desired, i.e. it is equal to (E*, T*) < (E, T). On the other hand, if (E_red, T_red) ≤ (E, T), the performance of the protection might be considered too far from the optimal and the measures might be considered unserviceable and demand replacement. If this is actually the case, until new protections are installed, the hazard at the locations on the slope beyond the current protection must be considered unmitigated, i.e. equal to (E, T). This comparison an requalification of rock fall hazard can effectively be performed and visualised with the help of (but not exclusively with) an intensity-frequency diagram, which defines hazard as a combination of rock fall energy on the y-axis and return period (or frequency of occurrence) on the x-axis. By identifying how the (E, T) point moves towards the (E*, T*) point on the diagram, for any location of a slope, it is possible to establish if and how hazard conditions vary at that location (and, by extension, all over the slope).

The workflow of the methodology can be summarised by the scheme in Fig. 1.

Fig. 1

Scheme of the methodology (modified from Prina Howald et al. 2017). The requalification of hazard explained in the text is performed according to the intensity-frequency diagram used in the Swiss Codes (Raetzo et al. 2002; Lateltin et al. 2005) for hazard assessment

2.2 Implementation into a spreadsheet

The method of evaluation of the effectiveness of rock fall protection—steps (a) to (c) presented in Sect. 2.1—was implemented into a Microsoft Excel-based tool, to allow for a quick, effective and systematic data collection and computation of the performance capacity of the measures, in terms of (E_red, T_red). The tool is composed by a Microsoft Excel spreadsheet and an optional form to be printed in hard copy.

The spreadsheet is subdivided into 3 sections (Steps A, B and C in Fig. 2), one for each corresponding step of the methodology. The first requires filling in information to identify and characterise the protection, such as name, date of construction, place of installation, type and performance capacity in terms of energy retention and return period, (E_opt, T_opt). The second is dedicated to the computation of the effective performance capacity (E_eff, T_eff) of the protection: all factors affecting that protection and belonging to Group 1 have to be listed here, together with the corresponding values assigned to the respective e_0,i and t_0,i penalty coefficients. Finally, the third section has exactly the same structure as the second and allows for the computation of the reduced performance capacity (E_red, T_red). Each factor j found to condition the behaviour of the protection in the current study and belonging to any Scenario k (from 1 to 6) is entered here, together with the corresponding assigned values for the penalty coefficients (e_k,i, t_k,j).

Fig. 2

Scheme of the evaluation tool implemented for site surveys and evaluation of the performance capacity of a rock fall protection measure

As the choice of values for the penalty coefficients e_0,i, t_0,i, e_k,j and t_k,j can be difficult (Prina Howald et al. 2017), the spreadsheet is designed to guide the user through this process. At first, only a qualitative evaluation of the influence of each factor on the performance of the protection is requested; the degree of severity of this influence is classified into 3 categories: low, moderate, high. Once such estimation has been performed by the user based on the state of the protection, the tool assigns automatically an interval of values corresponding to the degree of severity in input, retrieved from separate sheets containing this information for all the types of protections included in the methodology. These values aim to represent reasonable choices most likely to accommodate the majority of the applications (based on data collected on previous analyses and engineering judgement). Nevertheless, the user is afterwards free to manually adjust these sets of “suggested” values, to make them as much appropriate as possible for each specific situation studied. Criteria as much exhaustive as possible for establishing and validating the suggested values for the penalty coefficients are currently in course of development.

For what concerns the optional form to be printed and compiled on site, this constitutes a simplified version of the spreadsheet tool and is aimed only at data collection. It has the same structure as the spreadsheet, with the first section identical to the electronic version, but the following two only serving the purposes of noting which factors and faults affect the protections inspected and establishing a level of severity for each of them (low, moderate, high). The data is collected on paper during the inspection and then transferred to a computer for analysis and computation of the effectiveness of the protections inspected.

The tool is therefore meant to be used either in fully electronic format, by means of a tablet or similar device, if available, or paired with the form. The first option has the advantage that the data collection and evaluation of the condition of the protection can both be performed on site, inputting all the necessary data directly in the spreadsheet.

3 Application to a real case study

This section presents an application of the methodology at a site in Switzerland, Veytaux, located in the Canton of Vaud. This site is interesting under the point of view of the application of the methodology, as:

• important elements are threatened by rock falls and several protection measures were already installed in the past, through the years;

• hazard zoning maps were elaborated at the site, at first without accounting for rock fall protections and then in presence of rock fall protections.

It must be pointed out here that the purpose of this application is solely to show how the whole procedure presented in this paper works, from site surveying and inspecting existing protections to evaluating their effectiveness and assessing rock fall hazards accordingly. By no means this application intends to elaborate new maps and/or question the current maps elaborated and approved by the Cantonal Authorities. In this perspective, more specifically:

• the data and information regarding the protection measures investigated reflect their real situation for what concerns, position, type and current conditions; the trajectory simulations results illustrated, the intensity and hazard maps shown—with no account and with account for the effects of the protections—are the actual results of the hazard assessment performed and approved by the Cantonal Authorities;

• the qualitative assessment of the protections, the corresponding penalty coefficients, the specific (numerical) data on the frequencies of failure, percentage of blocks reaching a given point on the slope and associated kinetic energy values are based on assumptions made by the authors with the only purposes of:

  • (1) fulfilling the objective of the paper, that is, providing a clear, detailed and most informative example of how the evaluation of the performance capacity is carried out (as described in Sect. 2 and implemented in the MS Excel Spreadsheet), as well as how the final decision about the role of protection measures in hazard assessment and zoning can be taken, based on this evaluation;

  • (2) avoiding any conflicts/possible inconsistencies with the zoning maps available at the site and currently used for land use planning regulations.

The application was carried out with reference the intensity-frequency matrix diagram used in the Swiss Codes for hazard zoning (Raetzo et al. 2002; Lateltin et al. 2005), which features three categories of intensity, expressed by rock fall kinetic energy, three categories of frequency of occurrence, expressed by the return period, and three levels of hazard (low, moderate and high) resulting from the combination of these two parameters (Fig. 1). This diagram was used to elaborate all the hazard maps shown in the following sections and for performing the requalification of the hazard scenario based on the performance of the protection measures featured in the example.

3.1 Study area: characterisation of the site and hazard information

The location of the study area is shown in Fig. 3. The site is located on the slopes over the shores of Lake Geneva, between the cities of Montreux and Villeneuve, just south of the town of Veytaux.

Fig. 3

(Source: map.geoadmin.ch)

Location of the study area

The slopes are characterised by a height between 400 and 600 m, constituted by limestone formations (clayey limestone from the Middle Jurassic, compact limestone from the Late Jurassic, fractured fine limestone from the Late Cretaceous), moraine and scree deposits. These formations, combined with the steep slopes, make the area susceptible to release rock falls.

The elements potentially threatened by these phenomena are the Viaduct of Chillon, which constitutes a main highway route along the shore of Lake Geneva, the main Federal Railway Line connecting the Canton of Vaud with the Canton of Valais and, keeping on moving south, with Italy, a Cantonal Road following approximately the same path as the railway, as well as several buildings belonging to towns and villages along the lakeshore.

Protection measures existing in this area are constituted by different types of rock fall fences (Fig. 4), installed at several locations on these slopes since 1986 (those located just above the exposed elements mentioned) or, in some cases, even earlier (those located more upslope, closer to the rock fall source areas).

Fig. 4

(modified from ABA-GEOL)

Location of the barrier fences. In black: linear cliff sector considered in the study. In blue: representative profile selected for the application of the methodology

Rock fall hazard assessment and zoning were performed at the site by the geological/geotechnical firm ABA-GEOL SA, based on trajectory simulation results and according to the Swiss Codes and practices for landslide hazard assessment. The release areas of the blocks were detected by means of on site surveys for characterising the cliffs; regarding the frequency of failure, no single exact value was specified, as all possible events with a failure frequency higher or equal than 1/300 years⁻¹, i.e. T ≤ 300 years, were considered. A size of the blocks of about 3 m³ (1.8 m equivalent diameter) was determined and their trajectories were simulated with the 3D rock fall software PiR3D (Cottaz et al. 2010). Examples of results of trajectory simulations are presented in Fig. 5. Figure 6 shows the kinetic energies E associated to the rock fall paths, classified into 3 categories, according to Swiss practice, as follows: low (0 < E < 30 kJ), moderate (E < 300 kJ), high (E > 300 kJ). By combining rock fall frequencies of occurrence and kinetic energies, hazard zoning maps were elaborated, both without the effect of the barrier fences found on site (Fig. 7) and in presence of the barrier fences (Fig. 8), considered as fully functional.

Fig. 5

Example of rock fall simulation results obtained at the site of Veytaux (modified from ABA-GEOL). In black: linear cliff sector considered in the application. In yellow: representative 2D profile selected

Fig. 6

Map of rock fall intensity according to the Swiss Codes for hazard zoning (modified from ABA-GEOL). In white: linear cliff sector considered in the application. In red: representative 2D profile selected

Fig. 7

Hazard zoning map at Veytaux with no account existing protection measures (modified from ABA-GEOL). In white: linear cliff sector considered in the application. In yellow: representative 2D profile selected

Fig. 8

Hazard zoning map at Veytaux, accounting for the existing protection measures (n from ABA-GEOL). In white: linear cliff sector considered in the application. In yellow: representative 2D profile selected

3.2 Site inspection and data collection

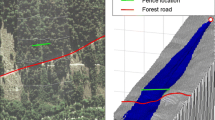
Starting from this information for the whole endangered area, for the sakes of clarity and simplicity, the example of evaluation of the effectiveness of the protections was focused on a specific 2D profile, representative of one specific linear section of unstable cliffs in the whole site, and involved only the barrier fences found along this profile. The final choice of the profile was made with the purpose of selecting a possible preferential path for blocks which would, at the same time, include barriers with interesting features in view of the application of the methodology, such as barriers already impacted by rock fall events, barriers situated in proximity of a stream or torrent, barriers which have already undergone some reparations, easily accessible for inspection, etc. In this respect, several barrier fences were inspected along possible rock fall propagation lines and, finally, those to be analysed in this application were chosen to be the fences names G4 and G7 (Fig. 4). In particular, this choice was based on the fact that their functions complement each other, they have already undergone rock fall events (major event for G4), they are easily accessible (and easy to be inspected) and are located in a sort of natural bottleneck between the cliffs and the lakeshore which leads to the viaduct, the railway, the Cantonal road and some buildings. Figures 4, 5, 6, 7 and 8 show in plan view the position of the unstable linear sector of cliff and representative profile selected, while Fig. 9 illustrates the altimetric features of the profile, along with the positions of the two barrier fences and the exposed elements to be protected.

Fig. 9

Longitudinal profile representative of the selected sector of the slope studied for the evaluation of the effectiveness of the protection measures found on site. x_G7, x_G4 and x_v mark the locations of barrier fence G7, barrier fence G4 and the Viaduct of Chillon, respectively

From available data sources and reports of the Canton and based on the site investigation carried out, types, characteristics and conditions of the barriers G4 and G7 are the following.

3.2.1 Barrier fence G7

It is a low energy vertical fence built between 1986 and 1987, with an energy absorption capacity of 200 kJ and a height of 3 m. It is located above an access path to a drinkable water reservoir. Significant displacement of material as well as signs of erosion could be observed right uphill, due to water runoff associated to rain events. During the inspection, the following aspects could be noticed:

• some light signs of erosion at the level of the foundation of the barrier fence, most probably linked to the runoff of rainwater (Fig. 10a);

  Fig. 10

  

  Inspection of barrier fence G7. a Signs of erosion at the foundations due to rainwater runoff; b fence partially filled by different types of materials; c trace of impact of a boulder on one of the posts

• the net of the barrier fence was partially filled up by different types of materials (Fig. 10b), such as rocks, wood and vegetation, which could have a negative impact on its effective height and, up to some extent, on the elastic behaviour of the barrier;

• a sign of (relatively light) impact of a boulder from a past event to one of the posts of the fence (Fig. 10c).

Based on this information, the factors to be accounted for in view of the analysis of the effectiveness of this fence can be defined and qualitatively evaluated. Table 1 lists all the factors included so far in the methodology which belong to Group 1 and Group 2. In particular, those defining Group 1 are valid in general for all types of protections (including fences), while those in Group 2 included in Table 1 are, in this case, specifically referred to low energy vertical barrier fences only. These lists of factors were defined after the inspection and the compilation of a rock fall protection measures database for the protection measures found in the Canton of Vaud (Grisanti and Prina Howald 2014).

Table 1 List of factors potentially affecting the effectiveness of rock fall protections: Group 1 (Scenario 0), all protections; Group 2 (Scenarios 1–6) for rock fall barriers

By comparing the information collected on site and the factors available in Table 1, it results that those relevant to the evaluation of the effectiveness of this barrier fence are therefore (1) the action of rainwater, causing erosion of the soil of foundation of the posts, (3) a loss of effective height of the barrier due to partially filled nets and (3) damages to the barrier support structures after impacts. It is worth noticing that the second and third factor detected, assigned as Scenario 4 factors, could belong also to Scenario 5 and Scenario 6, depending on the life span planned for the protection—in this case, no specific information about the life span was available and, at the same time, no specific sign of either life span attained or behaviour of the fence in residual conditions were detected, therefore the factors mentioned were classified as Scenario 4.

As mentioned in Sect. 2, the study of most suitable values for the penalty coefficients is still ongoing. For the purpose of this application, however, let it be assumed that, after correct calibration of the suggested penalty coefficients values, the spreadsheet tool provides the following values for both e_k,j and t_k,j, for each degree of severity of the factors to be accounted for:

• action of rainwater (erosion) low: 0.9–1.0; moderate: 0.75–0.9; high: 0.6–0.75;

• loss of height (partially filled net) low: 0.9–1.0; moderate: 0.75–0.9; high: 0.6–0.75;

• damages to supports after impacts low: 0.95–1.0; moderate: 0.8–0.95; high: 0.6–0.8.

If these suggested values are used and, in particular, a value approximately in the middle of each interval is selected, the penalty coefficients can be determined as listed in Table 2, which also summarises which Scenario they belong to, as well as the qualitative appreciation of their degree of severity, corresponding to the observations and evidences collected during the survey. As it can be noticed in Table 2, the erosion due to rainwater is considered to affect both energy and return period at the location of the barrier: on the one hand, if the foundation loses strength, the barrier does as well; at the same time, the soil eroded could generate displacements of the post which could partially reduce the barrier height (and allow more blocks to go further downslope). The loss of effective height, on the other hand, is essentially affecting the frequency of blocks travelling beyond the barrier, and therefore the return period. Finally, “Damages to supports after impacts” were in this study considered to mainly affect the energy absorption capacity of the barrier, even though, in the worst circumstances, a damaged post might partially compromise also the height of the fence, and therefore condition the frequency of block going beyond the fence (and, in turn, the return period). Due to the evidences collected on site, this factor was in the end estimated as negligible for this barrier fence (Fig. 10) and assigned a value of 1.0 (no effect).

Table 2 Inspection of barrier G7: evaluation of the factors influencing the behaviour of the protection and corresponding suggested values for the related penalty coefficients e_k,j and t_k,j

3.2.2 Barrier fence G4

This is also a low energy vertical fence built between 1986 and 1987, with the same design features as the G7 in terms of energy absorption capacity (200 kJ) and height (3 m). It is located above an asphalt road and one of the piles of the Viaduct of Chillon.

The issues observed for this barrier fence at the moment of the inspection can be summed up as follows:

• a certain degree of erosion at the foundation of the fence, again most probably linked to the runoff of rainwater (Fig. 11a);

  Fig. 11

  

  Inspection of barrier fence G4. a Signs of erosion at the foundations due to rainwater; b different types of materials located in close proximity of the fence; c trace of impact of a boulder on one of the posts

• quite some material (rocks, branches, etc.) located just before the fence which could easily be transported into the net in a very near future; this could lead to a partial filling of the net (Fig. 11b) and, in turn, generate issues similar to those mentioned for fence G7;

• a clear sign of impact of a boulder to a post (Fig. 11c). Former studies carried out on this site indicate that a major rock fall event occurred in spring 2012 and caused the destruction of a barrier installed above G4, next to G7 (barrier G1 in Fig. 4). This impact trace is likely to be a sign of that event.

These features are very similar to those characterising fence G7 and the same factors can be taken into consideration for this fence. Following similar assumptions and choices made for fence G7, the penalty coefficients can be determined in this case as presented in Table 3. It can be noticed that damages to the post are more important, in this case, than for barrier G7.

Table 3 Inspection of barrier G4: evaluation of the factors influencing the behaviour of the protection and corresponding suggested values for the related penalty coefficients e_k,i and t_k,i

3.3 Evaluation of the effectiveness of the protections

As it can be remarked by looking at Figs. 7 and 8, the first element exposed to rock fall hazards is the Viaduct of Chillon, a large part of which would be affected by a high hazard were it not for the presence of the rock fall fences—including those at the location of the 2D slope profile considered for this analysis. All the other elements threatened found when moving downslope (railway line, cantonal road, buildings) would be located in a moderate hazard zone, which according to the Swiss regulations for land use planning, still constitute a condition requiring protections. Once the protection measures are considered, the hazard is completely mitigated at all the areas beyond them (Fig. 8). It is therefore of the utmost importance to check that the barrier fences G7 and G4 work effectively in order to confirm that the level of mitigation desired can actually be achieved.

In order to illustrate how the computations for the evaluation of the performance capacity of rock fall protection are carried out, as well as to establish whether the protections can in fact mitigate hazard based on their current state, some specific values of rock fall frequency of failure, kinetic energy and frequency of reach are required (where the frequency of reach is here defined as the likelihood of a block to travel beyond a certain location along the slope, expressed as the percentage of blocks in a rock fall simulation which pass through a given location of the slope, calculated over the total number of simulated trajectories). In line with the considerations made at the beginning of Sect. 3 with regards to the scope of this paper, appropriate values will be assumed for the above-mentioned parameters, in compliance with the hazard zoning maps previously elaborated without and with protection measures (Figs. 7, 8).

For what concerns the rock fall frequency of failure, a value of 1/100 years⁻¹ will be considered in the following example. This choice can be justified by keeping in mind the difficulties and uncertainties affecting the estimation of return periods of landslide events, particularly long ones such as 100 and 300 years (Hantz et al. 2003; Fell et al. 2008; Hantz 2011). Qualifying and distinguishing appropriately what event would correspond to 100 years rather than 200 or 300 and what hazards would specifically be related to each of them still appears very complicated. It is therefore considered acceptable in what follows that a hazard map such as the one in Fig. 7 could in the end be associated to a return period of about 100 years. Furthermore, in absence of more detailed information released about the estimation of the failure frequency for the hazard assessment at the site of Veytaux, this choice also better explains the presence of a moderate hazard zone (blue zone) in the map, according to the Swiss matrix diagram, in comparison to a return period close to 300 years, for which the blue zone tends to vanish as close at T gets to 300 years.

When evaluating the role of the protections in the hazard assessment along the slope profile selected, particular attention will be paid to three locations: the two abscissas x_G7 and x_G4 corresponding to the positions of the barrier fences G7 and G4, respectively, and the abscissa x_v, corresponding to the position of the viaduct. More in detail, for the following three situations will be analysed for the three locations:

• (a) absence of barrier fences;

• (b) presence of barrier fences in optimal operating conditions;

• (c) presence of barrier fences in the current conditions after inspections.

3.3.1 Absence of barrier fences

Figure 12a illustrates, along the 2D profile selected, the same hazard scenario represented in plan view in Fig. 7, with no account for the existing protections.

Fig. 12

Hazard scenario and zoning along the reference profile selected, with no account for the protection measures present on site. Right: the Swiss intensity-frequency diagram shows where the (E, T) couples representing the hazard at x_G7, x_G4 and x_v can approximately be located on the diagram, i.e. what level of hazard affects them

Fig. 13

Hazard scenario and zoning at the reference profile, considering the effects of the two barrier fences on site at their optimal performance capacities. For comparison purposes, the hazard with no account for the protections is also shown. The intensity-frequency diagram on the left show how hazard evolves at x_G7, x_G4 and x_v

Fig. 14

Hazard scenario and zoning at the reference profile, considering the effects of the two barrier fences on site in their current performance capacities. For comparison purposes, the hazard with no account for the protections is also shown. The intensity-frequency diagram on the left show how hazard evolves at x_G7, x_G4 and x_v

Before the effects of the protection measures are considered, the energy at x_G7, x_G4 and x_v is high, i.e. E > 300 kJ, according to the intensity map in Fig. 4, which means the hazard is high based on the Swiss Codes—the (E, T) couples describing the hazard at these locations are all in the red domain of the intensity-frequency diagram in Fig. 12a. Let it be assumed that this “high” value of energy E is equal to 400 kJ at x_G7. Let it also be assumed that it decreases to E = 310 kJ at x_G4, implying an energy loss of 22.5% between these two locations, and then, as x_G4 is very close to the viaduct at x_v, that E decreases further, but only slightly, down to E = 305 kJ at x_v.

Regarding the frequency of reach P_r, under the hypothesis that only a small part of simulated trajectories stop before x_G7 due to the steep slope profile, it can be assumed that 90% of the total simulated blocks reach x_G7 and travel further downslope. Based on similar considerations, let the frequency of reach at x_G4 be 80% (i.e. 80% of the simulated blocks travelling beyond this location) and 78% at x_v, because of the very short distance between the fence G4 and the viaduct. For a failure frequency of 1/100 years⁻¹, the corresponding return periods at x_G7, x_G4 and x_v can be therefore be computed as follows: T(x_G7) = 100/0.90 = 111 years, T(x_G4) = 100/0.80 = 125 years and T(x_v) = 100/0.78 = 128 years, respectively (Fig. 12).

3.3.2 Presence of barrier fences in optimal operating conditions

In case of barriers G7 and G4 perfectly working, the hazard is completely mitigated beyond x_G4 according to Fig. 8 and as reflected along the 2D slope profile selected in Fig. 12. However, at x_G7 the energy of the event (400 kJ) is higher than the absorption capacity of this barrier fence (200 kJ). This means this barrier fence would be destroyed and blocks would go through it. As a first approximation, it can be considered that:

• the residual energy a block has after impact is given by the difference between its energy before impact and the capacity of the barrier fence G7, i.e.:

  E(x_G7) = 400 – 200 = 200 kJ;

• all the simulated blocks travel further downslope towards G4, according to the most unfavourable scenario following the collapse of G7, i.e.:

  P_r(x_G7) = 90% and T(x_G7) = 111 years

• the rate of energy loss along the paths of a block between x_G7 and x_G4 remains unchanged, i.e. ΔE = –22.5%

In these conditions, at x_G4 it results: E(x_G4) = 200 · (1–0.225) = 155 kJ, which means the energy absorption capacity of fence G4 in optimal working conditions (E_opt = 200 kJ) is higher than the energy of the blocks, i.e. the barrier works effectively and stops the rock fall. Let it be assumed that the trajectory simulation results show the barrier fence stops 70% of the simulated blocks (the rest might jump the barrier or go around it); consequently:

$$ T_{{{\text{opt}} }} \left( {x_{G4} } \right) = \, 100 \, / \, \left[ {0.80 \cdot \left( {1{-}0.7} \right)} \right] \, \approx \, 417\;{\text{years}} $$

which implies a frequency of reach P_r(x_G4) = 0.80 ·(1–0.7) = 24% (Fig. 12).

On this basis, at the location of the viaduct, as E_opt(x_G4) = 200 kJ > E(x_G4) = 155 kJ, it results that E(x_v) is, strictly speaking, equal to the energy of the few blocks still going over or around the barrier, the probability of reach is P_r(x_v) = 0.78 · (1–0.7) = 23% and the return period T (x_v) = 100/[0.78 · (1–0.7)] ≈ 427 years. The values obtained for (E, T) at x_v constitute a couple which, once superimposed to the Swiss intensity-frequency matrix diagram, is located outside of the diagram because of the high value obtained for the return period. In view of this, the energy E at this location is negligible (marked as E ≈ 0 in Fig. 12), whatever its value, as no hazard actually threatens it anymore due to an extremely low frequency of occurrence (T ≫ 300 years). Accordingly, the hazard is mitigated completely beyond the barrier fences (Figs. 8, 12), since this same conclusion can be drawn for all the other locations downslope, as the return period will keep on increasing downslope. Therefore, not only the viaduct, but also all the other elements potentially exposed located after it (railway line, Cantonal road, buildings) are in principle safe, despite the collapse of the upper fence, G7 (Figs. 13, 14).

3.3.3 Presence of barrier fences in the current conditions after inspections

For evaluating the effectiveness of the barrier fences G7 and G4 according to their actual conditions, as obtained from the field survey, their effective and reduced performance capacities have to be assessed.

Regarding fence G7, despite its failure occurring already at its optimal performance capacity, it can still be in principle interesting to evaluate its actual performance in terms of energy absorption, to determine how much the kinetic energy of a block going through it is in fact reduced. This might indeed influence the capabilities of fence G4 of retaining blocks. The computations of (E_eff, T_eff) and (E_red, T_red) for both barrier fences can easily be executed by means of the penalty coefficients defined in Tables 2 and 3 for each scenario involved, for each fence G7 and G4, respectively.

Using Eqs. (1) and (2), for G7 it can be written:

• evaluation according to Scenario 0

  $$ E_{\text{eff}} = E_{\text{opt}} *\mathop \prod \limits_{i} e_{0,i} = E_{\text{opt}} \cdot e_{0,1} = 200 \cdot 0.95 = 190\,{\rm kJ} $$

• evaluation according to Scenarios 1–6

  $$ E_{\text{red}} = E_{\text{eff}} *\mathop \prod \limits_{k} \mathop \prod \limits_{j} e_{k,j} = E_{\text{eff}} \cdot e_{4,5} = 190 \cdot 1.0 = 190 \,{\rm kJ} $$

Since no more blocks than the 90% of those going through the barrier can travel further downslope, the reduced capacity of the barrier in terms of return period does not need to be computed. As the actual value of energy absorption capacity has been updated to 190 kJ at x_G7, the blocks running through fence G7 will move downslope towards fence G4 with a higher energy than in case b), equal to E(x_G7) = 400 – 190 = 210 kJ. As done previously, if 22.5% of this energy is lost once the blocks reach x_G4, E(x_G4) = 210 ·(1–0.225) = 163 kJ.

The evaluation of the effectiveness of fence G4 can then be performed, as follows:

• evaluation according to Scenario 0

  $$ E_{\text{eff}} = E_{\text{opt}} *\mathop \prod \limits_{i} e_{0,i} = E_{\text{opt}} \cdot e_{0,1} = 200 \cdot 0.95 = 190 \,{\rm kJ} $$
  $$ T_{\text{eff}} = T_{\text{opt}} *\mathop \prod \limits_{i} t_{0,i} = T_{\text{opt}} \cdot e_{0,1} = 417 \cdot 0.95 = 396\,{\rm years} $$

• evaluation according to Scenarios 1–6

  $$ E_{\text{red}} = E_{\text{eff}} *\mathop \prod \limits_{k} \mathop \prod \limits_{j} e_{k,j} = E_{\text{eff}} \cdot e_{4,5} = 190 \cdot 0.87 \approx 165 \,{\rm kJ} $$
  $$ T_{\text{red}} = T_{\text{eff}} *\mathop \prod \limits_{k} \mathop \prod \limits_{j} t_{k,j} = T_{\text{eff}} \cdot e_{4,4} = 396 \cdot 1.0 = 396 \,{\rm years} $$

As obtained in case of barrier fence in perfect working order (case b), the energy at x_G4 (163 kJ) is, strictly speaking, still lower than the actual (reduced) energy absorption capacity of the barrier (165 kJ). The return period has slightly increased, but its value is still much higher than 300 years, which means, in this case as well, no hazard (residual only) starting from the location of this barrier—as this (E, T) couple would again be located outside the intensity-frequency matrix diagram.:

• E(x_G4) ≈ 0 kJ (or, as specified before, equal to the energy of the few blocks still going over or around the barrier)

• T (x_G4) ≈ 396 years

Proceeding downslope, at the location of the viaduct, this assessment is confirmed: by applying, to a first approximation, the same energy and return period reduction (i.e. same penalty coefficients) to all locations beyond the barrier fence, at x_v it results:

• evaluation according to Scenario 0

  $$ T_{\text{eff}} = T_{\text{opt}} *\mathop \prod \limits_{i} t_{0,i} = T_{\text{opt}} \cdot e_{0,1} = 427 \cdot 0.95 \approx 406 \,{\rm years} $$

• evaluation according to Scenarios 1–6

  $$ T_{\text{red}} = T_{\text{eff}} *\mathop \prod \limits_{k} \mathop \prod \limits_{j} t_{k,j} = T_{\text{eff}} \cdot e_{4,4} = 406 \cdot 1.0 = 406 \,{\rm years} $$

  and therefore:

• E(x_G4) ≈ 0 kJ in the sense specified for case b).

• T (x_G4) ≈ 406 years.

These results are summed up in Fig. 12.

4 Results

4.1 Interpretation of the results obtained from the application at the study site

The calculations performed in the previous section for obtaining:

• at x_G7:

• $$ E_{\text{eff}} = 190 \,{\rm kJ}\quad E_{\text{red}} = E_{\text{eff}} = 190 \,{\rm kJ} $$

  at x_G4:

  $$ E_{\text{eff}} = 190 \,{\rm kJ}\quad T_{\text{eff}} = 396 \,{\rm years} $$
  $$ E_{\text{red}} = 165 \,{\rm kJ}\quad T_{\text{red}} = 396 \,{\rm years} $$

  are exactly those performed as well by the spreadsheet tool introduced in Sect. 2.

As detailed in Sect. 2, then, the couples (E_red, T_red) must be compared with the couple (E, T) representing the hazard before the effects of the protections, to establish whether the mitigation the protections would guarantee in optimal conditions can still possibly take place. With reference to the previous example, this last part of the analysis can be performed by means of the computation of E(x_G7), E(x_G4), T(x_G4)—and E(x_v), T(x_v).

The evaluation carried out with the method presented allows to conclude that, based uniquely on the numerical results obtained and under the validity of the hypotheses made, the mitigation by means of barrier fences shown in Figs. 4 and 12 could actually take place. The corresponding areas are marked with a hatched texture which shows both the colours of the new hazard level achieved (white, i.e. no hazard) and the colour marking the hazard level in case no account for the protections is taken (i.e. red, in the former high hazard zone, or blue, in the former moderate hazard zone, closer to the shore). This new zoning can be considered as delineating a residual hazard, due to the fact that the current hazard level is negligible, but only because of the protection measures installed.

Nevertheless, important measures should be still taken regarding, at least, barrier fence G7. Whilst ordinary maintenance work would most likely be sufficient to restore G4 to its optimal performance capacity, a replacement of G7 with a higher absorption capacity barrier would be necessary.

Even in cases, like in this example, where more than one line of protections are installed at different locations down a slope, the fact of having one level of these protections (e.g. first line of barrier fences) destroyed by an event is not an acceptable option under many points of view (engineering, economic, political, social). In addition, the occurrence of such a failure could seriously compromise the good performance of the protections located downslope (like G4, in this case).

It is worth noticing, in terms of zoning, that the hazard between x_G7 and x_G4 should in principle be moderate (blue zone), because of an energy value between 30 and 300 kJ and a return period between 100 and 300 years. However, as barrier G7 is destroyed, the hazard is still marked with a red/blue hatched zone in Fig. 12. This is to remind, like it happens beyond x_G4, that the moderate hazard level is achieved only thanks to the presence of a protection measure—or more precisely, in this instance, at the cost of losing that protection measure.

4.2 Sensitivity analysis

This section introduces some preliminary analyses on the sensitivity of the approach proposed to the values assigned to the penalty coefficients.

Several aspects can be considered when defining how to vary the values of the coefficients, such as: (1) the boundaries of the intervals of values associated to the different degrees of severity (Sect. 3.2), (2) the selection criterion for picking values within these intervals, (3) the possibility of varying only one or rather several coefficients at the same time in a single analysis, as well as (4) the amplitude of the variation considered for each couple of coefficient (e_0,i, t_0,i) or (e_k,j, t_k,j)—i.e. the same for all coefficients or different. In addition, in case for a given factor n the influence on rock fall energy and return period would not be assumed to be the same, (5) different variabilities between e_0,n and t_0,n or e_k,n and t_k,n could also be investigated.

As an example for giving a first indication on how much sensitive the methodology is to the choice of the coefficients, their values in the analyses presented here were re-defined based on criteria (2) and (3), starting from the reference values used in the study in Sect. 3. Three new cases were investigated, using the same intervals of values for each degree of severity chosen in Sect. 3 (recalled in Table 4), and performing all computations according to the steps and hypotheses already shown.

Table 4 Preliminary sensitivity analysis on the influence of the values assigned to the penalty coefficients on the results of the methodology

Analysis (1) At first, a slight decrease only in the coefficients representing the erosion of the foundation due to rainwater runoff was considered. Both for barriers G7 and G4, coefficients e_0,1 and t_0,1 were reduced from 0.95 to 0.94. This allowed, on the one hand, to keep the basic idea of picking values approximately in the middle of the interval defining “low” severity (assumed not to change) and, on the other, to choose values slightly more on the safe side. Under these conditions:

• at x_G7:

  $$ E_{\text{red}} = E_{\text{eff}} = 188 \,{\rm kJ}\quad (T_{\text{red}} = T_{\text{eff}} = 111 \,{\rm years}) $$

  which yields E(x_G7) = (400–188) = 212 kJ and T(x_G7) = 111 years (same as in absence of barrier, due to the fact that the barrier is destroyed). Therefore, considering again an energy loss of 22.5% along the path between barriers G7 and G4, E(x_G4) = 164 kJ and:

• at x_G4:

  $$ E_{\text{red}} = E_{\text{eff}} = 164 \,{\rm kJ}\quad T_{\text{red}} = T_{\text{eff}} = 392 \,{\rm years} $$

As E(x_G4) = E_red(x_G4), the protection is barely able to stop the blocks and ensure a corresponding return period of 392 years. At the location of the viaduct, it consequently results E(x_v) = 0 and T(x_v) = 402 years, i.e. the hazard is, in principle, still mitigated and a zoning similar to that illustrated in Fig. 12 is obtained.

Analysis (2) Then, assuming that a better estimate of all coefficients involved would be obtained by selecting values between the lower bound and the mean value of each interval, the penalty coefficients were lowered to the values shown in Table 4 (column marked as “2”). On this basis:

• at x_G7:

  $$ E_{\text{red}} = E_{\text{eff}} = 186 \,{\rm kJ}\quad (T_{\text{red}} = T_{\text{eff}} = 111 \,{\rm years}) $$

  and therefore E(x_G7) = 214 kJ and E(x_G4) = 166 kJ. Since it results:

• at x_G4:

  $$ E_{\text{eff}} = 186 \,{\rm kJ} $$
  $$ E_{\text{red}} = 154 \,{\rm kJ} $$

  then E(x_G4) = 166 kJ > E_red(x_G4) = 154 kJ; this means not only barrier G7 but also barrier G4 is destroyed (which would imply E(x_v) = 11 kJ and T(x_v) = 128 years). No mitigation can occur and the hazard zoning to be considered should be the one represented in Fig. 12, where no protection is accounted for.

(3) Finally, by keeping still the same severity level for each factor, but taking values for each coefficient equal to the lower bound of the corresponding interval (Table 4, column marked as “3”), even more unfavourable conditions arose in terms of reduced performance capacity of the barriers, leading to:

• at x_G7:

  $$ E_{\text{red}} = E_{\text{eff}} = 180 \,{\rm kJ}\quad (T_{\text{red}} = T_{\text{eff}} = 111 \,{\rm years}) $$

  i.e. E(x_G7) = 220 kJ and E(x_G4) = 171 kJ, and:

• at x_G4:

  $$ E_{\text{eff}} = 180 \,{\rm kJ} $$
  $$ E_{\text{red}} = 144 \,{\rm kJ} $$

It is obtained again that barrier G4 is destroyed (E(x_G4) = 171 kJ > E_red(x_G4) = 144 kJ → E(x_v) = 26 kJ and T(x_v) = 128 years) and no mitigation can take place.

Table 4 summarises the results of these analyses, in comparison with the reference case.

From these analyses, it can be noticed that a very small variation in the values of the two coefficients (e_0,1; t_0,1) associated to the same factor (action of rainwater runoff) could produce quite significant changes to the results, at least in terms of possible hazard mitigation obtained. This is however due to the fact that, already in the reference case, the most critical factor for the verification of the reduced performance capacity, i.e. the energy absorption, was only very slightly higher than required for the mitigation. It appears therefore normal that in such a circumstance, a slightly more unfavourable value for one coefficient acting on the energy produces the effects mentioned.

On the other hand, similar variations on the values of the coefficients affecting the return period would have not compromised as easily the resulting performance, since the values of return period obtained would have been quite larger than the critical value of 300 years in the Swiss intensity-frequency diagram in all analyses carried out. This can be proved by imposing no modification in the energy absorption capacity of barrier G4 and studying only how the return period varies at x_G4 and x_v, as a function of the penalty coefficients defined in each analysis (Table 4):

• analysis 1: T_red(x_G4) = 392 years; T_red(x_v) = 402 years;

• analysis 2: T_red(x_G4) = 388 years; T_red(x_v) = 397 years;

• analysis 3: T_red(x_G4) = 375 years; T_red(x_v) = 385 years;

Further investigations are undoubtedly needed for a better insight on the sensitivity of the approach. However, these few examples may suggest that, if in principle the choice of different values for the penalty coefficients has always some influence on the performance capacity, consequences on the corresponding mitigation effects appear to become critical mostly as much as the difference (“margin of safety”) between the reduced performance capacity of a protection (E_red, T_red) and the values of energy and return period (E, T) at its location reduces.

5 Discussion

The methodology presented in this paper aims at providing an approach for a quick yet fairly complete characterisation of existing rock fall protections and for a preliminary evaluation of their actual effectiveness, based on their current conditions. Its application is quite easy in principle and the approach is flexible, but its core is based on a heuristic approach, relying on experience and engineering judgement, particularly for what concerns the penalty coefficients. Their evaluation should therefore be addressed carefully.

As mentioned in Sect. 2.1, estimating appropriate values for the penalty coefficients is complex, because of their number, the diversity of the factors they represent and the general lack of experiences and observations, which would help defining how to numerically quantify faults, malfunctions or possible effects of the environment on different types of measures.

Dealing with many different factors having as many different effects on the behaviour of rock fall protections is very challenging because, in many cases, the calibration of the corresponding penalty coefficients will require a different technique or method, according to the factor studied. In other words, estimating what impact a damaged element like a barrier post has on the general performance of the protection is not the same as trying to estimate to what extent and with what consequences a certain degree of corrosion of metallic elements of a given protection influences its behaviour. This, in turn, would be again different from predicting what loss of effective height a barrier fence, a dam or a retaining wall can have if materials are partially filling up their nets (barriers) or cumulating on their upslope face (dams, walls); and so on.

A few examples can be mentioned, under this point of view. With reference to Table 1, values for penalty coefficients accounting for factors such as a damaged post of a barrier fence, a point of weakness in the structure of a protection, the possibility of plastic deformations or the resistance to cyclic loading, could be assessed by implementing a finite element model of the protection measure, applying relevant forces representing the shock of a block hitting the measure and analysing the response of the model. On the other hand, other factors like the presence of outcropping rock or the loss of effective height of a barrier, dam or wall, due to materials and debris cumulated into/right behind the measure, could be taken into account directly in rock fall trajectory simulations. In the former case, the key point is to model appropriately the material covering the slope. In the latter, a protection with a lower height than the optimal should be considered in the analysis, and the percentage of trajectories (over the total) going beyond the protection in these conditions could be compared to the percentage of trajectories travelling beyond the protection in optimal conditions, in order to quantify how much the probability of reach increases with a faulty protection.

In addition to these considerations, and even when good calibration models are set up, all these evaluations require also a certain amount of engineering judgement, even more so for the effects of factors which are less predictable/quantifiable, such as corrosion of metal elements and erosion due to water running in proximity of the foundations of structural measures.

On top of this, considering that (1) many factors have been introduced in the methodology already, (2) that some are specific to each measure (Group 2) and (3) that new ones could be in principle added (the current list being not necessarily exhaustive), it is easy to understand that assigning proper values with a good scientific basis to all the penalty coefficients is quite a demanding task. As described previously, in order to better target the values of the coefficients to be used in the evaluations, the spreadsheet tool is designed to suggest relevant ranges of values, starting from a preliminary qualitative description of the state of the protection investigated (more adapted to a field inspection). However, even after completion of the calibration process in course, it must be once more remarked that the complete set of values the methodology will propose, and even more so the tentative values used in the example in this paper, should still be considered as reference values. These should be used with critical judgement in each study and it should be kept in mind that they could always be improved if supported by growing experience and/or new findings in this field.

As a closing note on the definition and use of the penalty coefficients, it must be remarked that the sensitivity of the methodology to the choice of the coefficients values should also be investigated thoroughly. As explained when presenting some preliminary analyses in Sect. 4.2, values for all penalty coefficients were changed so far only within the same intervals defining the degrees of severity introduced in the main application in Sect. 3; still, they could produced different results for very small variations, in terms of possible hazard mitigation. Despite this occurred due to a reduced performance of the protections already “near-critical” in the main study (reference case), these analyses showed that, at least in certain instances, hazard zoning results can change importantly according to the values of the coefficients, even when the qualitative degree of severity assigned to a given factor does not change. This may in principle happen because the choices for the quantitative values of the coefficients can depend on the number of degrees of severity defined and the amplitude of each corresponding interval of values. Further investigations are needed to provide a deeper knowledge in this respect and suggest a most suitable number of degrees of severity for fine-tuning at best the penalty coefficients values.

On the other hand, one of the biggest and most direct advantages of the methodology proposed, in addition to the simplicity of the operations to be performed, is its flexibility. The methodology does not feature any site-specific or rock fall scenario dependency and can be applied to any type of protection measure or combination of protections. Additionally, as mentioned above, it is open to the possibility of adding new factors and associated penalty coefficients not included so far—but still able to influence the behaviour of rock fall protection measures -, as well as to modify or update current values of the coefficients without any need for changing any other aspect concerning its application. Furthermore, even though the types of protections and the associated factors included in this methodology were defined starting from a database of rock fall protection measures present on the Swiss territory, new types of protection measures used in other countries could be added, if relevant. Also in relation to the original context in which the methodology was developed, despite it was at first designed (and applied in this paper) in compliance with the Swiss Codes for what concerns the use of the intensity-frequency diagram for hazard zoning, any intensity-frequency diagram can in fact be used in combination with this methodology. The use of one particular diagram is not binding and does not condition any step of application of the approach proposed. This also implies that it would be very straightforward to apply the methodology according to other national/regional guidelines (MATE/METL 1999; Interreg IIc 2001; AGS 2002), rock fall intensity-frequency diagram (Crosta and Agliardi 2003; Corominas et al. 2003; Jaboyedoff et al. 2005; Abbruzzese and Labiouse 2013) and, if present, corresponding land use regulations.

Finally, all these features allow not only to use the approach proposed in a number of possible problems in the sense specified above, but also to expand in an even broader sense the possibilities of its applications. In particular, a possible direction for new developments could be constituted by coupling the methodology presented with other procedures and techniques used in rock fall hazard assessment, for a more comprehensive evaluation of the potential risks affecting susceptible areas. For instance, in situations in which rock fall protections are equipped with monitoring systems to keep track of their performances in real time, the data obtained from monitoring could be used in combination with the methodology applied in this paper, in order to have a constant update on the state of operation of the protections. This would allow to re-compute the performance capacity of the existing measures continuously (or in correspondence of pre-defined levels of deformation and/or other relevant parameters provided by the instrumentation installed) and set alerts when specific thresholds for serviceability, previously established, are attained. Such a type of information could prove to be very valuable for real time decisions on whether to take the protections into account when evaluating imminent rock fall risks.

6 Conclusions

This paper presents a methodology for a quick yet effective evaluation of the performance of existing rock fall protection measures and their role in hazard zoning. The approach consists of two main phases. The first, a field survey, allows to collect data about the current state of rock fall protections at the study site and to compute the actual effectiveness of the protections present, according to a heuristic approach, based on coefficients (called “penalty coefficients”) representing factors potentially degrading the performance capacity of a rock fall protection during its life span. The actual effectiveness of the rock fall protections is quantified by their actual performance capacity. This parameter represents the ability of the protection of retaining energy and increasing return period (lowering the frequency of occurrence) at its location and beyond, after the relevant penalty coefficients have been applied to its optimal “as per design” performance capacity. The second part of the approach consists of an analysis comparing the computed actual effectiveness of the protection measure to the hazard affecting the site in absence of measures. Such comparison allows to establish whether, after the effects of the factors degrading its performance capabilities, the protection can still mitigate that hazard or, on the contrary, become unserviceable. In the first case, the hazard zoning maps can account for the presence of protections and display their mitigation effects (e.g. as residual hazard areas). In case of protection too damaged, instead, the hazard zoning displayed in the maps should neglect the presence of the measures, due to their unserviceability.

An application at a study site in Switzerland underlined the simplicity of operation of the methodology and the criteria for assessing rock fall hazard in presence of protection measures. The evaluation procedure tackles a point not deeply investigated so far in literature, it is easy to apply and features a good flexibility: it can be expanded and updated, in terms of rock fall protection measures and/or degrading factors to be included, it is applicable to any site, as well as according to any rock fall intensity-frequency diagram and, at a further stage, could even be coupled with other techniques used in rock fall hazard assessment, such as monitoring of the protections, for a more comprehensive real time evaluation of potential hazards and risks at a given site.