How much does the rainfall temporal resolution affect rainfall thresholds for landslide triggering?

Abstract

In many areas of the world, the prediction of rainfall-induced landslides is usually carried out by means of empirical rainfall thresholds. Their definition is complicated by several issues, among which are the evaluation and quantification of diverse uncertainties resulting from data and methods. Threshold effectiveness and reliability strongly depend on the quality and quantity of rainfall measurements and landslide information used as input. In this work, the influence of the temporal resolution of rainfall measurements on the calculation of landslide-triggering rainfall thresholds is evaluated and discussed. For the purpose, hourly rainfall measurements collected by 172 rain gauges and geographical and temporal information on the occurrence of 561 rainfall-induced landslides in Liguria region (northern Italy) in the period 2004–2014 are used. To assess the impact of different temporal resolutions on the thresholds, rainfall measurements are clustered in increasing bins of 1, 3, 6, 12 and 24 h. A comprehensive tool is applied to each dataset to automatically reconstruct the rainfall conditions responsible for the failures and to calculate frequentist cumulated event rainfall–rainfall duration (ED) thresholds. Then, using a quantitative procedure, the calculated ED thresholds are validated. The main finding of the work is that the use of rainfall measurements with different temporal resolutions results in considerable variations of the shape and the validity range of the thresholds. Decreasing the rainfall temporal resolution, thresholds with smaller intercepts, higher slopes, shorter ranges of validity and higher uncertainties are obtained. On the other hand, it seems that the rainfall temporal resolution does not influence the validation procedure and the threshold performance indicators. Overall, the use of rainfall data with coarse temporal resolution causes a systematic underestimation of thresholds at short durations, resulting in relevant drawbacks (e.g. false alarms) if the thresholds are implemented in operational systems for landslide prediction.

Introduction

Rainfall-induced landslides are among the most widespread and commonly occurring natural hazards in many areas of the world, with an increasing frequency in the last years (Gariano and Guzzetti 2016; Froude and Petley 2018; Haque et al. 2019). To predict the possible occurrence of these phenomena, landslide-triggering rainfall thresholds are often used. They are defined as the rainfall conditions that when reached or exceeded are likely to trigger landslides (Guzzetti et al. 2008). Several examples of rainfall thresholds exist in the literature, determined adopting either an empirical/statistical or a physically based approach, and providing numerous case studies at different temporal and spatial scales of analysis (De Vita et al. 1998; Guzzetti et al. 2007, 2008; Segoni et al. 2018a). In particular, empirical rainfall thresholds are determined by analysing past rainfall conditions that have presumably resulted in landslides. Despite some criticisms (Bogaard and Greco 2018), they are extensively adopted at various spatial scales for operational landslide prediction and early warning, particularly for shallow phenomena in wide areas (Intrieri et al. 2013; Chae et al. 2017; Greco and Pagano 2017; Piciullo et al. 2018; Segoni et al. 2018a, b; Guzzetti et al. 2020). The most used are the ID (rainfall mean intensity–rainfall duration) and the ED (cumulated event rainfall–rainfall duration) rainfall thresholds. The two approaches are analytically equivalent, since I = E/D. However, from a theoretical point of view, in the case of ED thresholds, the two variables are not dependent on each other; contrarily, in the case of ID thresholds, the rainfall mean intensity depends on the rainfall duration. For this reason, it is preferable to define ED thresholds, in which the two variables measure independent quantities.

The entire process that leads to the definition of empirical rainfall thresholds for landslide triggering was highly studied in the literature. Regarding the reliability and reproducibility of thresholds, many steps forward have been taken in recent years (Segoni et al. 2018a, b) aiming at solving critical issues, as:

• the definition of objective and automatic procedures to gather landslide and rainfall data, to reconstruct rainfall events and to define thresholds (Staley et al. 2013; Segoni et al. 2014; Lagomarsino et al. 2015; Iadanza et al. 2016; Vessia et al. 2016; Battistini et al. 2017; Piciullo et al. 2017; Rossi et al. 2017; Melillo et al. 2015, 2016, 2018);

• the adoption of rigorous validation procedures (Staley et al. 2013; Gariano et al. 2015a; Lagomarsino et al. 2015; Piciullo et al. 2017; Galanti et al. 2018);

• the evaluation and quantification of diverse uncertainties related to data and procedures (Gariano et al. 2015a; Nikolopoulos et al. 2014; 2015; Destro et al. 2017; Marra et al. 2017; Rossi et al. 2017; Peres et al. 2018; Marra 2019).

As a rule, the goodness and the reliability of empirical rainfall thresholds strongly depend on the quantity and the quality of rainfall and landslide data used for their definition.

Regarding the quantity of data, Peruccacci et al. (2012) pointed out that thresholds based on statistical analysis of empirical data are conditioned by the number and distribution of the DE pairs. In particular, they proposed a bootstrapping statistical technique to (i) identify the minimum number of rainfall conditions responsible for landslide triggering needed for obtaining reliable thresholds and to (ii) quantify the uncertainties associated with the parameters that define the thresholds. The same authors highlighted that the minimum number changes according to the distribution and the temporal resolution of the empirical DE data.

Moreover, Gariano et al. (2015a) highlighted how the validation of rainfall thresholds is hampered by lack of information on landslide occurrence. They observed that even a very small underestimation in the number of failures can produce a substantial reduction in the threshold validation performance.

On the other hand, the quality of rainfall and landslide data hampers the definition of the thresholds, introducing diverse uncertainties related to: (i) data incompleteness, lack of accuracy or errors in landslide catalogues; (ii) unavailability, gaps or errors in rainfall measurements, due to either manual or automatic data collection. To the above uncertainties, related to the input data, must be added those related to the adopted threshold model, i.e. (iii) lack of standardized criteria to identify landslide-triggering rainfall events; and (iv) lack of objective and reproducible methods used to determine the thresholds. Melillo et al. (2015) observed that standards for defining landslide-triggering rainfall conditions are lacking or poorly defined in the literature. Indeed, several articles regarding rainfall thresholds rarely report how the rainfall responsible for the landslide triggering is calculated (Segoni et al. 2018a), thus reducing also the possibility of comparing different thresholds. The majority of empirical rainfall thresholds available in the literature are still calculated using subjective and scarcely repeatable methods. Only a few attempts were recently made to define procedures for a standardized and reproducible—even automatized—calculation of landslide-triggering thresholds (see Melillo et al. 2018 and references therein).

Regarding the uncertainties related to landslide data, Peres et al. (2018) performed a quantitative analysis of the impact of the uncertainty in the landslide initiation time on the rainfall thresholds. The analysis was based on a synthetic database of rainfall and landslide information, generated by coupling a stochastic rainfall generator and a physically based slope stability model. Authors introduced errors in the timing of the landslide dataset simulating the way the information may be retrieved from newspapers and technical reports. The analysis showed that the impact of the uncertainties in the time of the failure can be significant, especially when errors exceed 1 day or when the estimated landslide-triggering time is earlier than the actual one. Generally, errors in the time instants lead to lower thresholds if compared with those obtained from an error-free dataset.

Concerning the temporal resolution of rainfall measurements, most of the thresholds published in the scientific literature were defined using hourly data, but still a relevant number rely on rainfall measurement with daily or even coarser resolutions (Segoni et al. 2018a). Very few thresholds were calculated using the finest (sub-hourly) resolution. Generally, daily rainfall was used in two main cases: (i) in areas where hourly resolution rain gauges are not available (e.g. Sengupta et al. 2010; Jaiswal and van Westen 2013; Jemec and Komac 2013; Tien Bui et al. 2013; Lainas et al. 2016; Palenzuela et al. 2016; Gariano et al. 2019; Dikshit and Satyam 2019; Soto et al. 2019) or (ii) in analyses covering long past periods when continuous hourly measurements are not available (e.g. Frattini et al. 2009; Berti et al. 2012; Gariano et al. 2015b; Zêzere et al. 2015; Vaz et al. 2018). For instance, Gariano et al. (2019) defined empirical cumulated event rainfall–rainfall duration (ED) thresholds for landslide triggering in a study area in south-western Bhutan using daily rainfall measurements. The defined thresholds are characterized by high uncertainties, which—as acknowledged by the authors—are attributable both to the limited number (43) of the reconstructed landslide-triggering rainfall conditions and the clustering effect of the DE pairs (i.e. the points representing the rainfall conditions in the D–E logarithmic plane), due to the daily temporal resolution of the rainfall.

Several works have tried to quantify the influence of diverse uncertainties related to rainfall data in the definition of rainfall thresholds. In particular, it was observed that the uncertainty affecting rainfall data deeply influences the calculation of the thresholds and can result in an overestimation of the failures, and consequently in a relevant number of false alarms when applied in early warning systems (Nikolopoulos et al. 2014; Marra et al. 2017; Peres et al. 2018). Nikolopoulos et al. (2014) analysed the effect of the rain gauge location and density of the rainfall network in the calculation of the thresholds, showing that rainfall measurements from gauges located far away from the debris flow can considerably lower the thresholds. Furthermore, Marra et al. (2014) and Nikolopoulos et al. (2015) confirmed that thresholds for debris flow occurrence obtained using rainfall measured from rain gauges are systematically lower if compared with those defined using radar rainfall estimates. Marra et al. (2016) and Destro et al. (2017) proved that this underestimation is due to the spatial non-stationarity of the rainfall fields, whose behaviour is related to the return period of the rainfall responsible for the failure.

Recently, in an inspiring work, Marra (2019) proposed a numerical, synthetic experiment that foregrounded how the use of rainfall data with coarse temporal resolution causes a systematic overestimation in the duration of the landslide-triggering rainfall events, with implications on the definition of rainfall thresholds.

Starting from this last experiment, this work analyses how the rainfall temporal resolution influences the definition of rainfall thresholds, their validation and the uncertainty associated with them. For the purpose, a real case study based on hourly rainfall series and accurate spatial and temporal information on rainfall-induced landslides is considered. Rainfall measurements are clustered in increasing bins of 1, 3, 6, 12 and 24 h (i.e. decreasing temporal resolutions), and for each bin the landslide-triggering rainfall conditions are defined. Then, the frequentist ED thresholds are calculated and validated using well-established methods and tools (Brunetti et al. 2010, 2018; Peruccacci et al. 2012; Gariano et al. 2015a; Melillo et al. 2018).

Methods and data

Algorithm for the calculation of landslide-triggering rainfall conditions and rainfall thresholds

For the calculation of the rainfall conditions responsible for landslide triggering and of the rainfall thresholds, the tool CTRL-T (Calculation of Thresholds for Rainfall-induced Landslides-Tool; Melillo et al. 2018) is used. The algorithm included in CTRL-T is written in R open-source software and is structured in three consecutive blocks, as described by Melillo et al. 2018. In the first block, the reconstruction of single rainfall events from continuous rainfall series is executed. A rainfall event is defined as a period, or a group of periods, of continuous rainfall separated from previous and subsequent events by a dry (i.e. without rainfall measurements) period. The parameters needed for the separation of rainfall events, including the length of the dry periods, are related to the climate conditions of the area (Melillo et al. 2015). A warm (from May to September) and a cold (from October to April) season are considered; consequently, a minimum dry period of 48 h and 96 h is considered to separate two consecutive events in the warm and in the cold season, respectively. In the second block, for each individual landslide, the representative rain gauges are selected in a predefined buffer around the failure, and the related rainfall events are calculated. For the purpose, geographical information on the location of rain gauges and landslides in the test site are used. Then, using the landslide temporal information, the rainfall conditions likely associated with each landslide are selected. Afterwards, the multiple rainfall conditions (MRC) likely responsible for each landslide are reconstructed and a weight w—which is a function of the distance between the rain gauge and the landslide, the duration and the cumulated rainfall—is assigned to each MRC. Finally, for each landslide, the MRC with the maximum w (named Maximum Probability Rainfall Condition, MPRC) is selected as the one likely responsible for the failure. In the third block, rainfall thresholds at different non-exceeding probabilities are calculated using all the MPRC associated with the landslides. A detailed description of CTRL-T can be found in Melillo et al. (2018).

Method for the definition of rainfall thresholds

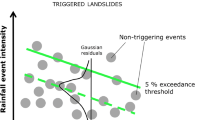
Cumulated event rainfall—rainfall duration (ED) thresholds are calculated adopting the frequentist method proposed by Brunetti et al. (2010) and updated by Peruccacci et al. (2012). According to this method, the threshold is represented by a power law curve, as in the following equation:

$$E = \left( {\alpha \pm \Delta \alpha } \right) \cdot D^{(\gamma \pm \Delta \, \gamma )}$$

(1)

where E is the cumulated event rainfall (in mm), D is the duration of the rainfall event (in h), α is the intercept (scaling parameter), γ is the slope (the scaling exponent) of the curve and Δα and Δγ are the uncertainties associated with α and γ, respectively. With this method, objective and reproducible thresholds at different non-exceedance probabilities can be calculated. As an example, the thresholds at 5% non-exceedance probability (considered as reference in this work) should leave 5% of the empirical DE pairs (MPRC) below itself. Threshold parameters are obtained from 5000 synthetic series of MPRC, randomly selected with replacement, generated by a bootstrap nonparametric statistical technique included in the algorithm (Peruccacci et al. 2012; Melillo et al. 2018). Therefore, α and γ are the mean values of the parameters, while Δα and Δγ are their standard deviations. The parameter uncertainties depend mostly on the number and the distribution of the MPRC. Peruccacci et al. (2012) found that in central Italy the minimum number of rainfall conditions needed for obtaining stable mean values of the parameters α and γ (i.e. reliable thresholds) is 75. However, this lower end may change slightly according to the distribution and dispersion of the empirical data points in the DE domain. Moreover, they observed that with more than 100 points, the uncertainties Δα and Δγ are markedly reduced and the thresholds become more reliable (Peruccacci et al. 2017).

Validation procedure

For the validation of the thresholds, the quantitative procedure introduced by Gariano et al. (2015a) and Brunetti et al. (2018) is adopted. The procedure is based on a sequence of steps: first, the dataset is randomly divided into a calibration subset and a validation subset. More in detail, 70% of the landslide-triggering rainfall conditions (i.e. MPRC) are randomly selected to calculate the rainfall thresholds, and the remaining 30% are used for threshold validation. Second, for the whole investigated period, all those rainfall conditions that have (presumably) not triggered landslides are also reconstructed by CTRL-T. Third, the rainfall threshold at 5% non-exceedance probability calculated using the calibration subset is compared both with the MPRC included in the validation set and with the rainfall conditions that have not triggered landslides. Therefore, a contingency table containing four possible contingencies can be defined. In the DE plane, a true positive (TP) is a landslide-triggering rainfall condition located above the threshold, while a true negative (TN) is a rainfall condition not resulting in landslides located below the threshold. On the other hand, a false positive (FP) is a rainfall condition without landslides located above the threshold, while a false negative (FN) is a landslide-triggering rainfall condition located below the threshold.

From the contingency table, two skill scores can be directly calculated:

• the true positive rate (TPR), or probability of detection (POD), that represents the fraction of landslides correctly predicted, i.e. the portion of MPRC above the threshold, TPR = TP/(TP + FN);

• the false positive rate (FPR), or probability of false detection (POFD), that defines the proportion of rainfall conditions without landslides above the threshold, i.e. landslides predicted but not occurred, FPR = FP/(FP + TN).

TPR and FPR are combined linearly to define the Hanssen and Kuipers discriminant (HK = TPR − FPR), also known as true skill statistic (Peres and Cancelliere 2014), which measures the accuracy in the prediction of both events with and without landslides. Moreover, FPR and TPR are used as x- and y-values, respectively, to draw the receiver operating characteristic (ROC) curve, useful for testing the predicting capability of the thresholds (Fawcett 2006; Gariano et al. 2015a; Piciullo et al. 2017). The combination of values TPR = 1 and FPR = 0 (i.e. the upper left corner of the ROC plot) represents the optimal point, given that is achieved when neither FN nor FP occur. When TPR increases and FPR decreases, the point that represents the threshold moves towards the optimal point, resulting in an increase in the threshold validation performance. Therefore, the Euclidean distance δ of the point representing the threshold from the optimal point can be also used as a measure of the goodness of the threshold.

The random selection of the calibration and validation subsets and the comparison of the last one with the threshold are repeated 100 times, in order to obtain 100 values of contingency and related skill scores. Finally, the mean values of the contingencies and skill scores are calculated and used to evaluate the threshold.

Study area and data

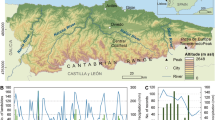
The study area is Liguria (5410 km²), an administrative region in NW Italy. Hourly rainfall data measured in the period March 2001–December 2014 by 172 rain gauges (average density of about one station every 31 km²) are used. The network is managed by the Hydrological Weather Observatory of the Liguria region (Osservatorio Meteo Idrologico della Regione Liguria). Additionally, spatial and temporal information on 561 rainfall-induced shallow landslides occurred in Liguria in the period October 2004–November 2014 are used. Figure 1 portrays the location of the landslides (white dots) and the rain gauges (black triangles). Detailed information about type, source of information and spatial and temporal accuracy of the landslides can be found in Melillo et al. (2018).

Fig. 1

Map of the test site showing the location of 561 landslides (white dots) and 172 rain gauges (black triangles) used to calculate rainfall thresholds. Background image from Google^®

Datasets for threshold calculation

Starting from the original rainfall series at hourly temporal resolution, four additional time series are created by aggregating the initial hourly measurements at increasing time steps of 3, 6, 12 and 24 h, to mimic a degraded temporal resolution of the input data. These five periods are chosen to investigate the effect of sub-daily temporal resolutions and to use aggregation times typical of instruments which measure (or estimate) the rainfall. Moreover, the maximum aggregation period is set at 24 h because the landslide catalogue contains shallow failures, for which even using daily rainfall data should be avoided.

Therefore, combining the landslide information and, in turn, the five rainfall series, five sets of (generally) different DE pairs (i.e. calculated at 1, 3, 6, 12 and 24 minimum time step) are reconstructed by means of CTRL-T. Then, five thresholds at 5% non-exceedance probability are defined and the uncertainties associated with their parameters are evaluated. Finally, the thresholds are validated using the above-described procedures. The obtained results are shown and discussed in the following sections.

Results

Landslide information and rainfall measurements clustered at five increasing temporal intervals provide 440 MPRC per each temporal resolution. One MPRC can be generally associated with more than one landslide. Then, ED 5% thresholds are calculated using 309 MPRC (70%) randomly extracted and are validated using 131 MPRC (30%).

Table 1 reports the main features of the 309 MPRC reconstructed at increasing temporal bins. Figure 2 shows the 309 DE pairs for the five temporal aggregations and the corresponding frequentist thresholds at the 5% non-exceedance probability. The threshold equations are reported in Fig. 2a–e, with data shown in log–log coordinates. A comparison among the five thresholds is shown in Fig. 3, both in logarithmic and in linear coordinates.

Table 1 Summary, for the five temporal aggregations, of the main features of the MPRC, of the threshold parameters and related uncertainties and of the E value for a duration of 24 h

Fig. 2

ED graphs showing the MPRC calibration datasets for a 1-h, b 3-h, c 6-h, d 12-h, e 24-h temporal aggregations, and the corresponding thresholds at 5% non-exceedance probability. Data are shown in logarithmic coordinates. Shaded areas portray uncertainty regions of the thresholds. Panel f shows the values of the ratio between the threshold parameters obtained at 1 h temporal resolution and those corresponding to the coarser resolutions, α_i/α₁ and γ_i/γ₁, as in Marra (2019). Bars represent the variation of the ratio

Fig. 3

aED thresholds at 5% non-exceedance probability, for the five calibration datasets at 1-, 3-, 6-, 12- and 24-h temporal aggregations, shown in logarithmic coordinates. b The same thresholds shown in linear coordinates in the range 1 < D ≤ 120 h, a typical duration range used in operational landslide prediction

As the temporal resolution of rainfall data degrades from 1 to 24 h, the following results are obtained:

• (i) the minimum, average and maximum values of event duration and cumulated event rainfall increase, meaning that the point clouds shift to the right in the D–E plane;

• (ii) the clustering of the empirical data points, more visible at short durations as a function of the aggregation bin, increases;

• (iii) at short durations, the DE pairs span a larger interval in the cumulated rainfall values;

• (iv) the scaling parameter, α, decreases and the shape parameter, γ, increases, resulting in steeper thresholds (Fig. 3);

• (v) quantitatively, the ratio between the threshold parameters obtained at 1 h temporal resolution and those corresponding to the coarser resolutions (Fig. 2f) changes as in Marra (2019), decreasing for α (− 45%) and increasing for γ (+ 30%);

• (vi) the parameter uncertainties, and consequently the threshold uncertainty regions, increase (Table 1); in particular, the α relative uncertainty increases significantly from 11.8% (1 h) to 16.4% (24 h);

• (vii) the E values on the threshold curves corresponding to D = 24 h strongly decrease, particularly after the 6-h temporal aggregation, resulting in a significant underestimation of the rainfall. Note that 24 h is a critical time interval in early warning procedures; in particular, a reduction of almost 20% of E is observed when the temporal resolution decreases from 1 h to 24 h.

As a result of the validation procedure, no significant variations are observed for the five datasets. Table 2 reports the mean values, retrieved from the 100 validation iterations, of the four contingencies (TP, FP, FN and TN) and the four skill scores (TPR, FPR, HK and δ) obtained for the five temporal aggregations (1, 3, 6, 12, 24 h). Figure 4 shows the variability ranges, as box-and-whisker plots, of the four skills scores.

Table 2 Mean values of contingencies and skill scores obtained from the validation procedure, for the five temporal aggregations. The optimal value for TPR and HK is 1, while for FPR and δ is 0

Fig. 4

Box-and-whisker plots showing median values (thick lines), 25th and 75th percentiles (top and bottom of the rectangular boxes) and the interquartile ranges (whiskers) of TPR, FPR, HK and δ skill scores for the five temporal aggregations

The mean values of TP and FN (and consequently of TPR) are the same for the five temporal aggregations. Note that the number of rainfall conditions that have triggered landslides (i.e., the sum of TP and FN) remains the same because a rainfall condition is always associated with a landslide, independently on the rainfall temporal resolution. However, obtaining the same mean values of TP, FN and TPR (even with a certain variability) for the five temporal resolutions confirms the reliability of the thresholds.

Conversely, the mean values of FP and TN decrease as the temporal resolution becomes coarser. This is related both to the method used to reconstruct and separate two consecutive rainfall conditions and to the validation procedure. In fact, for the five temporal aggregations, the length of the dry periods used to separate two consecutive rainfall events remains the same, while the rainfall measurements are aggregated at increasing intervals. Therefore, when using coarser resolutions some short events reconstructed using finer resolutions might aggregate in a single longer event. As a consequence, the number of rainfall conditions decreases as the temporal resolution becomes coarser from 1 to 24 h. In addition, the validity range of the thresholds is set by the minimum and maximum duration of the rainfall conditions used for their definition. Consequently, all the events with duration shorter or longer than this range cannot be included in the validation. Since the calibration and validation subsets are extracted randomly, some conditions selected for validation could fall outside the threshold domain, therefore reducing the number of FP and TN. This is observed more frequently using coarser resolutions due to the increasing clustering of the rainfall conditions.

Furthermore, the values of FPR, HK and δ are very similar, though the best values of HK and δ are found at 6 h aggregation, together with a higher variability range. This can be observed also looking at Fig. 4, in which a few differences between the skill scores calculated for the five aggregations can be detected. In particular, the (slightly) better values of HK and δ obtained for 6 and 24 h are due to the lower amount of FP compared to TN (i.e. lower FPR), related to the characteristics of the rainfall conditions reconstructed with these temporal resolutions. However, differences among skill scores in the five cases are very minimal; therefore, the rainfall temporal resolution does not affect significantly the validation results.

Discussion

Generally, the sources and characters of uncertainties can be categorized as either aleatory or epistemic (Der Kiureghian and Ditlevsen 2009). Aleatory uncertainties reflect the intrinsic randomness of a natural phenomenon; the possibility of reducing it is not foreseen. Conversely, epistemic uncertainties are related to the lack of knowledge about the phenomenon, e.g. lack of data or measurements; therefore, they can be reduced by gathering more (and more precise) data or by refining models (Der Kiureghian and Ditlevsen 2009). Most of the uncertainties in natural hazard analysis and prediction involve both types. This is also the case for empirical rainfall thresholds for landslide triggering. The uncertainties analysed in this work are epistemic, since they are related to the temporal resolution of rainfall data and the number of rainfall measurements. Therefore, they can be reduced by adopting the finest resolution available. In fact, using coarse (particularly, daily) resolution, a wide range of empirical data points, i.e. rainfall conditions, with large durations are obtained, thus resulting in a scattered distribution of the rainfall conditions in the DE plane at short durations. This produces a huge increase in the relative uncertainties of the thresholds (Table 1). Such an issue is of great importance if the thresholds are to be used in operational systems for landslide prediction and early warning. Thresholds with high uncertainty cannot be considered reliable. Moreover, low and steep thresholds, obtained from rainfall measurements aggregated at 24 h, might result in a high number of FP (false alarms). The increase in the steepness of the thresholds defined with coarser temporal resolutions (Fig. 3, Table 1) might result in more FP at shorter durations and more FN (missed alarms) at larger durations. In a threshold-based warning system, frequent FN should be avoided to increase the system efficiency, and repeated FP should be avoided in order to increase the credibility of the system, limiting the “crying wolf syndrome” (Breznitz 1984).

Conclusions

The main findings of this work can be summarized as follows:

• (i) rainfall temporal resolution does affect considerably the calculation of empirical rainfall thresholds for landslide triggering, resulting in marked variations of the shape and the validity range of the threshold curves, but it does not affect significantly their validation;

• (ii) the use of coarse rainfall temporal resolution results in steeper thresholds (i.e. lower thresholds at short durations, up to 1 day) and in a huge increase in the uncertainties of the threshold parameters, with relevant drawbacks and implications in the application of the thresholds in operational systems for landslide prediction.

These findings, anticipated by the results of the synthetic experiment conducted by Marra (2019), are here confirmed by means of a dataset related to a real case study.

Further analysis on the uncertainty evaluation will be useful for refining and improving the calibration and the validation of the thresholds, which still must be considered essential tools for the operational prediction of rainfall-induced landslides in large areas.

Finally, the outcomes of the present work recommend that:

• (i) rainfall thresholds defined using daily data must be represented by equations or graphs portraying D in days instead of hours. This would keep the theoretical reliability of the thresholds, which are valid only for values of D multiple of 24 h;

• (ii) a proper threshold validation, i.e. done using an independent validation dataset, is necessary to prove the effectiveness of the thresholds; validation must be performed using the same rainfall temporal resolution used in calibration;

• (iii) when the rainfall thresholds are used in operational landslide early warning systems, the temporal resolution of the prediction must be the same used in the definition of the thresholds.