Mining exploitation influence range

Abstract

Mining exploitation has a negative impact on the natural environment. Voids created in the rockmass result in displacements and deformations of land surface. During planning and conducting the exploitation, the range of exploitation influence in the form of linear deformations is being determined. On the basis of mining-geological parameters of exploitation, the exploitation range of influences is calculated. According to the literature, many different ranges of exploitation influences can be determined depending on what has been the purpose of it. Different types of exploitation influence ranges can be distinguished, such as theoretical, damage or measurable. In the paper, the matters connected with determining those three types of the influence range are taken under consideration. The comparison of magnitudes of determined influence ranges is illustrated with two practical examples.

1 Introduction

The mining exploitation is causing the occurrence of voids in the rockmass. The void, moving towards the land surface, results in the occurrence of linear deformations—subsidence as well as nonlinear ones—e.g., craters, cracks (Lee and Abel 1983). Due to the fact that the mining exploitation is conducted on a big area and for a long time, it is challenging to monitor exploitation effects as well as to determine its influence range (Peng 1986; Sroka et al. 2011).

The term ‘mining exploitation influence range’ is not easily and unambiguously definable one. This issue can be treated as the philosophical one. In the literature on the one hand, there are many different definitions of exploitation influence range (Darling 2011; Sinclair Knight Merz Pty Ltd. 2014); on the other hand, the determination of fixed range borders seems to be questionable. If dynamical influences are taken into account (paraseismic mining shakings of the ground, rock bursts), the effects of such a phenomenon could be registered tens of kilometres from the epicentre, where no other influences are not registered.

When analysing the process of deformation in time and space as well as the possibilities of measuring this process, many different definitions of an influence range can be inferred. There are three basic ways to determine the exploitation influence range.

• 1. The theoretical (model) influence range r_t

• 2. The damage influence range r_d

• 3. The measurable influence range r_m

According to some of modelling theories, the range of linear deformations is never-ending just like the probability in accordance with the normal distribution theory. On the basis of the most popular theories of deformations forecasting (geometric-integral theories), the border of theoretical range of exploitation linear deformations influences can be determined. In accordance with the Budryk–Knothe theory (Knothe 1984; Kratzsch 1983), one of the parameters is the angle of the main influences range, what has an impact on the radius of the main influences range, but this parameter is not directly the theoretical influence range (r_t).

The mining exploitation has a negative impact on the natural environment. The exploitation is a threat to the safety of people and objects located within its influence range. The construction works specialists determine the resistance of buildings to mining exploitation influence on the basis of states of the bearing capacity and of the serviceability. Those border states determine the state of object’s deformation and possibility of its usage. From this point of view, it is crucial to determine the harmfulness of the exploitation influence for construction objects. Therefore, the next border value can be determined, which is the damage influence range (r_d).

Significantly different is the approach of the land surveyors to this issue. When measuring on the land surface the results of ongoing mining exploitation, they highlight limitations of accuracy of conducted measurements of displacements and deformations. From this point of view, a deformation or a displacement is registered only when the magnitude of this parameter is higher than the error occurring during its determination, this is that the displacement is significant from the measuring point of view or it can be treated as the measurement error. In this situation, there can be distinguished the measurable influence range (r_m).

In the paper, there is presented the analysis of rules for determining the mining exploitation influence range in accordance with theoretical considerations. There is also suggested the definition of a theoretical influence range.

2 Theoretical models

The theoretical models, which are used to forecast deformations caused by the underground mining exploitation, allow to determine the spatial distribution of deformations caused by the underground mining exploitation. In the literature, different theoretical solutions based on different foundations can be found (Chugh et al. 1989; Darling 2011). Those models are using the group of parameters which allow to connect mining-geological conditions of the exploitation with deformations caused by this exploitation (Ambrožič and Turk 2003). Among many other theoretical solutions, the geometric-integral methods are the most popular in Europe and two of such models are used in the paper.

The geometric-integral theory (Kratzsch 1983; Peng 1986; Karmis et al. 1990; Ren et al. 1987) is based on acknowledging of the appropriate influence function f, which allows to determine the impact of single element of the mining exploitation (an elementary exploitation) on points of the rock mass and the land surface (Fig. 1). Using the superposition principle of influence, the elementary influences (from an elementary exploitation) are added what results in displacements. A vertical displacement can be described with below equation:

$$S_{\text{A}} = \iint\limits_{P} {f\left( {x,y} \right){\text{d}}P}$$

(1)

where S_A—a theoretical subsidence in point ‘A’, f(x, y)—an influence function, dP—a surface area of an element of exploitation.

Fig. 1

Elementary point subsidence due to the elementary exploitation

The selection of an influence function and model’s parameters are determining the obtained results of the forecast. The remaining parameters of deformation in vertical dimension (tilt T, curvature K) are appropriate derivatives for vertical displacements (Kratzsch 1983). On the other hand, regarding parameters in horizontal dimension (horizontal displacement U, horizontal strain ε), the most popular theoretical solution is the Aviershin’s formula (Aviershin 1947) which makes horizontal displacements dependant on the gradient of the subsidence and horizontal deformations dependant on the curvature:

$$U = - bT$$

(2)

$$\varepsilon = - bK$$

(2a)

where ‘b’ is a proportionality coefficient, which magnitude Avieshin made dependant on the exploitation depth (0.16H). The magnitude of this coefficient has been the subject of many researches and publications (Hejmanowski and Kwinta 2009). The magnitude of the coefficient was tried to be variant in time and space, but solutions obtained have been too complicated as well as they have not brought any measurable benefits. In Polish, mining the Aviershin’s formula was used by Budryk and suggested the higher magnitude of this coefficient (Budryk 1953).

2.1 Knothe’s theory

This theory is a basic solution that is being used in Polish mining (Knothe 1984). This is due to the fact that with this theory the results of calculations are highly accurate in comparison with the measurements, and still this theory remains very simple and the physical meaning has been given to the parameters of this theory (Hejmanowski and Malinowska 2009). The theory is used to forecast deformations caused by the underground exploitation of different useful minerals (Hejmanowski 1993). Currently, this model functions accurately enough for mining practice aims in many different variants of computer software.

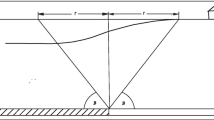
As in Fig. 2 for flat state of deformation in order to describe a profile of a subsidence, Knothe parameterised the Gauss function with comparing it to a triangle. As a result of such an action, he obtained the influences function in form (2):

$$f_{\text{K}} (x) = S_{\hbox{max} } \frac{1}{{r_{\text{K}} }}\exp \left( { - \pi \frac{{x^{2} }}{{r_{\text{K}}^{2} }}} \right)$$

(3)

where f_K(x)—the Knothe’s influences function, S_max = a · M—a maximum final subsidence, a—an exploitation coefficient, which depends on the way in which the after-exploitation void has been filled, M—a thickness of the layer of bed to be exploited, $r_{\text{K}} = \frac{H}{tg\beta }$—a parameter of influence dispersion—a radius of the main influence range, H—a depth of the bed to be exploited (m), β—an angle of the main influence range in the Knothe’s theory.

Fig. 2

Reproduced with permission from Knothe (1984)

Radius of influence r and the angle of main influence range β

In the Knothe’s theory, as it can be seen above, a radius of the main influence range is unambiguously defined. On the other hand, an angle of the main influence range (β) is one of two basic parameters of the Knothe’s theory. An angle of the main influence range is connected with physical–mechanical properties of the rock mass, and it allows to describe in the very simple way really complex structure and properties of the rock mass. A radius of the main influence radius is linearly related to the depth of exploitation. As a result of the parameterisation of the Gauss function, the influence reaches further than the magnitude of radius of the main influence range. In many publications, the extent of the influence range angle on the basis of the Knothe’s theory has been indicated for different geological layers in Poland. As an example for the bituminous coal exploitation in Upper Silesian Coal Basin (Polish: Górnośląskie Zagłębie Węglowe—GZW), this parameter can be assumed to have a value of 67.6 grad. A maximum final subsidence that is present in Eq. (3) also depends on one of the parameters, which is the way in which the after-exploitation void has been filled as well as the introduced methods of exploitation. Regarding the Polish mining in GZW for the longwall exploitation, this parameter is being calculated between 0.7 and 0.9 (on average 0.8). What has to be taken into account is the fact that the parameters for certain conditions of conducting the exploitation are the most accurately calculated on the basis the empirical data (conducted exploitation supervised with geodetic measurements). When the dependency (3) is put into Eq. (1), vertical displacements can be determined and afterwards the rest of deformation indicators can also be determined. The theory is simple, but to receive accurate results, it is needed to have some experience in calculating as well as to have the set of parameters adequate to conditions of conducted exploitation (Kwinta 2011).

2.2 Ruhrkohle’s theory

This theory, as well as the Knothe’s theory presented in previous part, is the geometric-integral theory in which the proper influence function has been adopted (Ehrhardt and Sauer 1961; Hejmanowski 1993; Preusse 1990). In literature the theory is known as the Ruhrkohle’s theory or as the Ehrhardt–Sauer’s theory (Kratzsch 1983; Sroka et al. 2011). The authors of this theory have adopted the exponential function as the Knothe influence function, but they have parameterised it differently (Cain and Zimmerman 2016). The influence function in the Rurhkohle’s method for a one-dimensional variable has a form:

$$f_{\text{R}} (x) = S_{\hbox{max} } \sqrt {\frac{k}{\pi }} \frac{1}{{r_{\text{R}} }}\exp \left( { - k\frac{{x^{2} }}{{r_{\text{R}}^{2} }}} \right)$$

(4)

where f_R(x)—the Ruhrkohle’s influence function, S_max—a maximum subsidence, k = − ln (0.01)—a constant value. $r_{\text{R}} = \frac{H}{tg\gamma }$—a parameter of the influence dispersion (radius of the main influence range), H—a depth of the bed to be exploited (m), γ—an angle of the main influence range in the Ruhrkohle’s theory.

In Fig. 3, the elementary exploitation has been depicted, which generates the subsidence with the volume of 99.8% of the volume of the exploitation on the length equal to a radius of the main influence range.

Fig. 3

Elementary exploitation in the Ruhrkohle’s theory

When analysing (4), it is noticed that also this theory is using two model parameters to calculate the deformation indicators. Also in this theory, the basic values of the parameters have been defined. For the caving exploitation a factor is determined a priori within the range from 0.9 to 1.0. On the other hand, an angle of influence range, its magnitude for calculations is conventionally accepted as over 50 grad. The relation between the Knothe’s theory presented above and the Ruhrkohle’s theory can be reduced to a dependency between angles of the main influence range (Sroka et al. 2015):

$$\sqrt \pi \cdot tg\beta = \sqrt k \cdot tg\gamma$$

(5)

In the Ruhrkohl’s theory similarly to the Knothe’s theory, the Aviershin’s formula can be used to determine the indicators in the horizontal plane.

3 Theoretical influence range

The theoretical influence range (r_t) is connected with the basis of deformation forecasting theory adopted for calculations. In case of geometric-integral theories, the range angles, which are their basic parameters, determine how far the influences of forecasted deformations reach. Below the analysis what values particular indicators has is presented. In order to analyse, some simplifications of calculations are introduced in the form of exploitation which generates flat area of displacements. Schematically such an area is depicted in Fig. 4.

Fig. 4

Assumed theoretical exploitation in the form of so-called half-plane

For the exploitation presented in Fig. 3, during formulation of the virtual variable of the integration λ, the equation of the subsidence profile is obtained and then other deformation indicators are obtained with calculations of other derivatives and with usage of the Aviershin’s formula. To simplify the notation and the analysis, additional dependences are introduced. The integration variable x is standardised to the radius of the influence range, what means that the new variable has been introduced:

$$\eta_{i} = \frac{x}{{r_{i} }}$$

(6)

where i stands for the chosen forecasting theory.

Next the ancillary variable is introduces, that is the variability coefficient which is the relative magnitude of deformation indicator δ_P, which determine the percentage magnitude of the deformation indicator to its maximum value:

$$\delta_{\text{P}} = \frac{{P\left( {\eta_{i} } \right)}}{{P_{\hbox{max} } }}100\%$$

(7)

where P stands for any defined deformation indicator.

With those assumptions, the magnitude of the theoretical influence range can be determined for underground mining exploitation.

The vertical subsidence for flat state of deformation on the basis of the Knothe’s theory and with the presented assumptions can be depicted as:

$$S(x) = S_{\hbox{max} } \int\limits_{{\eta_{\text{K}} }}^{ + \infty } {\exp \left( { - \pi \lambda^{2} } \right)} {\text{d}}\lambda$$

(8)

and certain relative indicators values (7) take form of:

$$\delta_{\text{S}} \left( {\eta_{\text{K}} } \right) = \int\limits_{{\eta_{\text{K}} }}^{ + \infty } {\exp \left( { - \pi \lambda^{2} } \right){\text{d}}\lambda } \cdot 100\%$$

(9)

$$\delta_{\text{T}} \left( {\eta_{\text{K}} } \right) = \delta_{\text{U}} \left( {\eta_{\text{K}} } \right) = \exp \left( { - \pi \eta_{\text{K}}^{2} } \right) \cdot 100\%$$

(10)

$$\delta_{\text{K}} \left( {\eta_{\text{K}} } \right) = \delta_{\varepsilon } \left( {\eta_{\text{K}} } \right) = \sqrt {2\pi } \eta_{\text{K}} \exp \left( {0.5 - \pi \eta_{\text{K}}^{2} } \right) \cdot 100\%$$

(11)

On the other hand, for the Ruhrkohle’s theory the equation is:

$$S(x) = S_{\hbox{max} } \sqrt {\frac{k}{\pi }} \int\limits_{{\eta_{\text{R}} }}^{ + \infty } {\exp \left( { - k\lambda^{2} } \right)} {\text{d}}\lambda$$

(12)

and relative indicators values for this theory take form of:

$$\delta_{\text{S}} \left( {\eta_{\text{R}} } \right) = \sqrt {\frac{k}{\pi }} \int\limits_{{\eta_{\text{R}} }}^{ + \infty } {\exp \left( { - k\lambda^{2} } \right){\text{d}}\lambda } \cdot 100\%$$

(13)

$$\delta_{\text{T}} \left( {\eta_{\text{R}} } \right) = \delta_{\text{U}} \left( {\eta_{\text{R}} } \right) = \exp \left( { - k\eta_{\text{R}}^{2} } \right) \cdot 100\%$$

(14)

$$\delta_{\text{K}} \left( {\eta_{\text{R}} } \right) = \delta_{\varepsilon } \left( {\eta_{\text{R}} } \right) = \sqrt {2k} \eta_{\text{R}} \exp \left( {0.5 - k\eta_{\text{R}}^{2} } \right) \cdot 100\%$$

(15)

According to the dependence (5), formulas (8)–(11) correspond directly to formulas (12)–(15). In Fig. 5, the distributions of relative values of indicators (9)–(11) and (13)–(15) are depicted.

Fig. 5

Distribution of variability coefficients for deformation indicators

The magnitudes of the variability coefficient in numerical form are compiled in Table 1.

Table 1 Magnitudes of variability coefficients of indicators in the function of the distance from the verge of exploitation in the Knothe’s and the Ruhrkohle’s theories

As it can be seen in Fig. 4 and in Table 1 for the distance from the exploitation levelling with the radius of the main influence range, the magnitudes of indicators can be significant. For subsidences, this indicator equals about 0.6% of the maximum value; for gradients of subsidence profile and horizontal displacements, the magnitude of the variability indicator equals about 4% of the maximum value; and for the curvatures of the subsidence profile and horizontal deformations, the variability coefficient equals about 18% of the maximum magnitude of those indicators. Obviously the relative magnitudes depend to large extend on the intensity of the exploitation. For exploitations which causes big magnitudes of deformations indicators, within the distance of the main influence radius the magnitudes of deformations indicators can be significant. In general, for practical solutions it can be assumed with appropriate accuracy that the influence range in accordance with both the Knothe’s and the Ruhrkohle’s theories equals 1.5 of the radius of the main influence range in that particular theory.

4 The damage influence range

Along with definitions presented in the introduction, the paper is focusing now on the damage influence range. The experts in construction works in the mining exploitation areas as a result of long-term researches and analysis, they have come up with the conclusion that the border values of deformation indicators can be calculated, for which lower magnitudes of indicators are practically imperceptible in objects (Kwinta and Gawronek 2016). The below border values of the damage influence can be accepted (Malinowska and Hejmanowski 2010; Sroka et al. 2011):

$$\begin{array}{*{20}l} { \bullet \quad {\text{vertical}}\;{\text{gradients}}\;{\text{of}}\;{\text{the}}\;{\text{subsidence}}} \hfill & {T_{\text{b}} = 0.5\,{\text{mm/m}},} \hfill \\ { \bullet \quad {\text{radius}}\;{\text{of}}\;{\text{the}}\;{\text{curvature}}\;\left( {{\text{reciprocal}}\;{\text{of}}\;{\text{the}}\;{\text{vertical}}\;{\text{curvature}}} \right)} \hfill & {R_{\text{b}} = 40\,{\text{km}},} \hfill \\ { \bullet \quad {\text{horizontal}}\;{\text{strain}}} \hfill & {\varepsilon_{\text{b}} = 0.3\,{\text{mm/m}}} \hfill \\ \end{array}$$

On the basis of accepted magnitudes of damage influence border values for chosen deformation indicators, the damage influence range can be formulated as:

$$r_{\text{d}} = \hbox{max} \left\{ {r_{{{\text{d}}|{\text{T}}}} ,r_{{{\text{d}}|\upvarepsilon}} ,r_{{{\text{d}}|{\text{R}}}} } \right\}$$

(16)

where

$$\begin{aligned} r_{{{\text{d}}|{\text{T}}}} & = x\left( {T_{\text{b}} } \right) \\ r_{{{\text{d}}|\upvarepsilon}} & = x\left( {\varepsilon_{\text{b}} } \right) \\ r_{{{\text{d}}|{\text{R}}}} & = x\left( {R_{\text{b}} } \right) \\ \end{aligned}$$

This formula picks the biggest influence range from all deformations indicators which are taken into consideration.

In order to determine the distance from the exploitation in which the damage influences occur, the theories presented in the previous part of the paper are being used. As previously, the flat state of deformations (Fig. 3) is taken into considerations. In this case, the formulas to calculate the distance from the edge of the exploitation to the place where border deformations values occur can be formulated.

Firstly the damage influence range for gradients of the subsidence profile is analysed. For both theories, the equation for the tilt takes the form of:

$$T\left( x \right) = S_{\hbox{max} } \frac{1}{{r_{\text{K}} }}\exp \left( { - \pi \frac{{x^{2} }}{{r_{\text{K}}^{2} }}} \right)$$

(17)

$$T\left( x \right) = S_{\hbox{max} } \sqrt {\frac{k}{\pi }} \frac{1}{{r_{\text{R}} }}\exp \left( { - k\frac{{x^{2} }}{{r_{\text{R}}^{2} }}} \right)$$

(18)

In order to determine the damage influence range, dependencies (17) and (18) have to be transformed. When using the elements introduced earlier, the below dependencies are formulated:for the Knothe’s theory

$$r_{{{\text{d}}|{\text{T}}}} = r_{\text{K}} \sqrt {\frac{{\ln T_{\hbox{max} } - \ln T_{\text{b}} }}{\pi }}$$

(19)

where $T_{\hbox{max} } = \frac{{S_{\hbox{max} } }}{{r_{\text{K}} }}$

For the Ruhrkohle’s theory

$$r_{{{\text{d}}|{\text{T}}}} = r_{\text{R}} \sqrt {\frac{{\ln T_{\hbox{max} } - \ln T_{\text{b}} }}{k}}$$

(20)

where $T_{\hbox{max} } = \frac{{S_{\hbox{max} } }}{{r_{\text{R}} }}\sqrt {\frac{k}{\pi }}$.

Unfortunately the simple transformation is not possible with regard to the curvature and displacement radius, and the determination of the damage influence radius is connected with conducting iterative calculations.

Firstly the considerations for the Knothe’s theory are presented. The appropriate formula for the radius of the subsidence curvature takes the form of:

$$R_{\text{K}} \left( x \right) = \frac{{r_{\text{K}}^{3} \exp \left( {\pi \frac{{x^{2} }}{{r_{\text{K}}^{2} }}} \right)}}{{2\pi S_{\hbox{max} } x}}$$

(21)

The iterative equation for the damage influence range on the basis of the formula for the curvature radius is formulated:

$$r_{{{\text{d}}|{\text{R}}}} = x_{0} \frac{{2\pi x_{0}^{2} + r_{\text{K}}^{2} \left( {\frac{{R_{\text{b}} }}{{R\left( {x_{0} } \right)}} - 2} \right)}}{{2\pi x_{0}^{2} - r_{\text{K}}^{2} }}$$

(22)

In this equation, x₀ is the approximate magnitude of the damage influence range and in next iteration steps the magnitude used for calculations is the one computed in the previous iteration step. As the initial magnitude for this variable, the radius of the main influence range in the theory r_K is adopted.

For the Ruhrkohle’s theory, those formulas take the form of:

$$R_{\text{R}} \left( x \right) = \frac{{r_{\text{R}}^{3} \exp \left( {k\frac{{x^{2} }}{{r_{\text{R}}^{2} }}} \right)}}{{2kS_{\hbox{max} } x}}\sqrt {\frac{\pi }{k}}$$

(23)

$$r_{{{\text{d}}|{\text{R}}}} = x_{0} \frac{{2kx_{0}^{2} + r_{\text{R}}^{2} \left( {\frac{{R_{\text{b}} }}{{R\left( {x_{0} } \right)}} - 2} \right)}}{{2kx_{0}^{2} - r_{\text{R}}^{2} }}$$

(24)

In this case, as the initial magnitude x₀, the radius of the main influence range r_R is also adopted.

Similar iterative calculations can be conducted for horizontal strain (the initial magnitudes are adopted in the same way as for the curvature radius) and below equations are formulated:for Knothe’s theory

$$\varepsilon_{\text{K}} \left( x \right) = \frac{{2\pi S_{\hbox{max} } bx}}{{r_{\text{K}}^{3} }}\exp \left( { - \pi \frac{{x^{2} }}{{r_{\text{K}}^{2} }}} \right)$$

(25)

$$r_{{{\text{d}}|\upvarepsilon}} = x_{0} \frac{{r_{\text{K}}^{2} \frac{{\varepsilon_{b} }}{{\varepsilon \left( {x_{0} } \right)}} - 2\pi x_{0}^{2} }}{{r_{\text{K}}^{2} - 2\pi x_{0}^{2} }}$$

(26)

for Ruhrkohle’s theory

$$\varepsilon_{\text{R}} \left( x \right) = \frac{{2kS_{\hbox{max} } bx}}{{r_{\text{R}}^{3} }}\sqrt {\frac{k}{\pi }} \exp \left( { - k\frac{{x^{2} }}{{r_{\text{R}}^{2} }}} \right)$$

(27)

$$r_{{{\text{d}}|\upvarepsilon}} = x_{0} \frac{{r_{\text{R}}^{2} \frac{{\varepsilon_{\text{b}} }}{{\varepsilon \left( {x_{0} } \right)}} - 2kx_{0}^{2} }}{{r_{\text{R}}^{2} - 2kx_{0}^{2} }}$$

(28)

Using the above formulas, the damage influence range can be determined, when the basic geometric parameters of the exploitation, the exploitation system and the parameters of the calculations model are known.

5 The measurable influence range

The last analysed type of the influence range is the measurable influence type that is the distance from edge of the exploitation to the place where deformations indicators can be determined on the basis of the conducted geodetic measurements (Darling 2011; Kratzsch 1983; Unlu et al. 2013).

Primarily the states of the deformation process had been characterised only descriptively. Along with the development of the geodetic instruments and of the calculations methods, more and more modern geodetic methods of measurements were used. One of the most important developments was the introduction of the digital rangefinder, which allowed to obtain more accurate measurements results. Next significant improvement in the measurements methods was the usage of the GPS satellite system (Liu et al. 2012). The emergence of the GNSS satellite systems (Havasi 2012) has allowed to obtain the results of completely new quality along with limiting the time consumption and the costs of conducting the observations (lack of the need of the long-time reference of measurements to fixed points). The development of the satellite technologies, particularly of the space-based radars, causes the next approach revolution in the area of measuring the deformations on the land surface. It has become possible to determine even small deformation magnitudes for huge areas. Therefore, the SAR technology is going to be used more and more often when the exploitation influence range is determined (Cheng et al. 2016; Milczarek et al. 2017).

Unfortunately the results of the deformations measurements, which allows to describe the state of the process, contain also the probabilistic information. The geodetic measurements due to the technological reasons are burdened with different factors which results in occurrence of the random, systematic errors and outliers. Also the medium (the rock mass) is very changing and heterogeneous, what causes the occurrence of significant disturbances in the deformation picture. As a result of all those reasons, it is impossible to unambiguously determine the border of the influence range on the basis of measurements. By using the statistical methods, the border of the range with the analysis of the accuracy can be determined.

Depending on the measurement methodology used to determine the deformations in the mining areas, the different accuracies of the determination of displacements and deformations are obtained. To be able to talk about the displacement determined on the basis of measurements, the magnitude of the displacement has to be bigger than the magnitude of the error with which this value has been obtained. Therefore, the influence range border obtained on the basis of measurements depends on the applied measurements methodology.

Similarly to other methods of determining the influence range, the maximum magnitude of the measureable influence range can be determined from among the ranges for individual deformation indicators. Therefore, the equation for the measurable influence range can be formulated as:

$$r_{\text{m}} = \hbox{max} \left\{ {r_{{{\text{m}}|{\text{T}}}} ,r_{{{\text{m}}|\upvarepsilon}} ,r_{{{\text{m}}|{\text{S}}}} } \right\}$$

(29)

where individual ranges have to be lower than average errors of determining them

$$\begin{aligned} & r_{{{\text{m}}|{\text{T}}}} \left( {T > pm_{\text{T}} } \right) \\ & r_{{{\text{m}}|\upvarepsilon}} \left( {\varepsilon > pm_{\upvarepsilon} } \right) \\ & r_{{{\text{m}}|{\text{S}}}} \left( {S > pm_{\text{S}} } \right) \\ \end{aligned}$$

where p is the level of trustfulness (single, double or triple magnitude of the standard error).

The measurements are being taken in individual series independently; therefore, to determine errors the propagation of a standard error can be used. Taking into considerations the fact that measurements in individual series should be taken ‘in the same way’, the errors in individual series can be assumed to be identical. For the levelling measurements, it is assumed that the error of determining the height is presented as m_H, and for the distance measurements, the error is presented as m_d; then, the errors of the deformations indicators are formulated as below:for subsidences

$$m_{\text{S}} = m_{\text{H}} \sqrt 2$$

(30)

for tilt

$$m_{\text{T}} = \frac{1}{d}\sqrt {2m_{\text{S}}^{2} + T^{2} m_{\text{d}}^{2} } \approx \frac{{2m_{\text{H}} }}{d}$$

(31)

for strain

$$m_{\upvarepsilon} = \frac{{m_{\text{d}} }}{d}\sqrt 2$$

(32)

On the basis of above-mentioned formulas and assuming the standard magnitudes of measurement errors, the measurable influence range for the most popular measuring methods equals (with the average distance between measuring points d = 20 m): for the satellite visualizations (SAR), it can be assumed that m_S= 3 mm.

Obviously the higher accuracy is expected, and the costs and time consumption of the measurements are growing significantly.

Taking into considerations only measurements errors connected with accidental errors of the measuring methods, the magnitudes of measurable influence range which are obtained are exaggerated. Due to the fact that the random dispersion is occurring in connection with the deformation process, the level of trustfulness has to be increased (e.g., p = 2); then, the measurable influence range is significantly shorter.

6 Examples of influence ranges calculation

The example 1 is depicting the issue of designing the exploitation that fulfils specified land planning requirements. The mining entrepreneur, that obtained the permission to exploit the field within the mining area (Fig. 6), wants to obtain for exploitation new parts of the field and expand the mining area in the future. For some reasons, the new exploitation has to be designed, which is not going to impact the area of the commune—smallest unit of the administrative division in Poland (marked in red in Fig. 6—part of the commune area within the field area).

Fig. 6

Scheme of the analysed terrain

On the basis of the geological data of the identified field as well as the exploitation parameters in neighbouring mining terrains, the below Knothe’s theory parameters can be adopted:

$$\begin{aligned} & M = 2.50\,{\text{m}};\quad a = 0.6;\quad S_{\hbox{max} } = 1.50\,{\text{m}} \\ & H = 600\,{\text{m}};\quad tg\beta = 1.7;\quad r_{\text{K}} = 352.0\,{\text{m}} \\ & b = 96.0\,{\text{m}} \\ \end{aligned}$$

Therefore, for such an exploitation, the maximum magnitudes of deformation indicators equal:

$$S_{\hbox{max} } = 1.50\,{\text{m}};\quad T_{\hbox{max} } = 4.26\permille;\quad K_{\hbox{max} } = 0.018\,{\text{km}}^{ - 1} ;\quad R_{\hbox{min} } = 54.33\,{\text{km}};\quad \varepsilon_{\hbox{max} } = 1.77\permille$$

The theoretical influence range r_t equals (on the basis of Table 1):

$$\begin{aligned} & r_{\text{t}} = 528\,{\text{m}} \\ & S\left( {r_{\text{t}} } \right) = 0.15\,{\text{mm}};\quad T\left( {r_{\text{t}} } \right) = 0.004\permille;\quad \varepsilon \left( {r_{\text{t}} } \right) = 0.009\permille \\ \end{aligned}$$

The damage influence range r_d equals (for the border damage magnitudes as in the Sect. 4):

$$r_{{{\text{d}}|{\text{T}}}} = 291\,{\text{m}};\quad r_{{{\text{d}}|\upvarepsilon}} = 355\,{\text{m}}$$

Therefore, the damage influence range amounts r_d= 355 m.

For the curvature radius, it is impossible to determine the damage influence range, because the minimum curvature radius that has been calculated is bigger that the border damage magnitude (40 km).

The measurable influence range can be determined assuming that the levelling measurements are taken with the precise subsidence method (Table 2) and in the horizontal plane are taken with the angular-linear method (Table 3). The length of the measuring segment amounts d = 24 m. Additionally taking into considerations the random dispersion of a phenomenon and the measurement errors, the higher level of trustfulness has to be adopted that means p = 2. On the basis of that as well as on the basis of formulas (9)–(11), the below can be formulated:

$$\begin{array}{*{20}l} m_{\text{S}} = 1.4\,{\text{mm}}\quad r_{{{\text{m}}|{\text{S}}}} = 407\,{\text{m}} \\ m_{\text{T}} = 0.08\permille \quad r_{{{\text{m}}|{\text{T}}}} = 360\,{\text{m}} \\ { m_{\upvarepsilon } = 0.12\permille \quad r_{{{\text{m}}|{\upvarepsilon }}} = 370\,{\text{m}}} \\ \end{array}$$

Therefore, in accordance with Eq. (29) the measurable influence range is in the distance r_m= 407 m from the exploitation edge.

Table 2 Levelling measurements

Table 3 Distance measurements (determining of deformations)

In Fig. 7, the edges of the designed exploitation are presented in accordance with different definitions of the influence range.

Fig. 7

Edges of the acceptable exploitation in accordance with different influence ranges

Depicted in Fig. 7, the routes of the acceptable deployment of the exploitation edge do not differ significantly, but the determination of the volume of the field excluded from the exploitation is impressive. The magnitudes of the surface area and the volume of the field excluded from the exploitation are presented in Table 4.

Table 4 Losses caused by the exploitation limitations

The difference between the exploitation volume in the theoretical range and in the damage range equals almost 1.7 million cubic metres. Therefore, the application of the damage influence range has an economical justification. Of course the most optimal solution is to reach an agreement with the commune and to exploit within the whole field with the protection of individual objects from the mining exploitation impact.

The example 2 concerns the exploitation in the Ruhr region (Busch et al. 2015, 2017; Preusse 1990). The designed exploitations in this case had the borders of influence range determined on the level of 1 mm. It was the theoretical influence range which was causing many problems starting from the big distances from the exploitation to the problems with verification of the exploitation effects on the basis of measurements. Taking the damage influence range as the referential one, the analysis is conducted how the influence range is going to change when the theoretical range (1 mm) is replaced with the damage influence range.

For calculations, the standard parameters of the Erhardt–Sauer’s theory were included in the theoretical calculations for the Ruhrkohle’s theory:

$$\begin{array}{*{20}l} {{\text{parameter}}\;{\text{of}}\;{\text{the}}\;{\text{main}}\;{\text{influence}}\;{\text{range}}} \hfill & {\gamma = 50\,{\text{grad}}} \hfill \\ {{\text{exploitation}}\;{\text{factor}}} \hfill & { \, a = 0.9} \hfill \\ \end{array}$$

For indicators in the horizontal plane, the Aviershin formula (2a) is adopted.

Taking into considerations the exploitation that has been conducted in the Ruhr region in last few years, the below geometric range of exploitation is adopted:

$$\begin{aligned} {\text{depth}}\;{\text{of}}\;{\text{the}}\;{\text{exploitation}}\;\left( {\text{H}} \right) :\; 6 0 0 { - 1300}\,{\text{m}} \hfill \\ {\text{thickness}}\;{\text{of}}\;{\text{the}}\;{\text{exploitation }}\left( {\text{M}} \right) :\;1.0{ - }4.0\,{\text{m}} \hfill \\ \end{aligned}$$

For the data adopted as above, the distribution (in function H and M) is determined, in what distance from the exploitation the subsidence equals 1 mm (13). Next the distribution of the damage influence range has been determined (16). Then, it is determined the percentage by which the influence range is going to change when the theoretical influence range is replaced with the damage influence range. The results of calculations are depicted in Fig. 8.

Fig. 8

Distribution of the damage influence range decrease relative to the theoretical influence range (1 mm) in the Ruhr region

It can be acknowledged that in this case the damage influence range is going to decrease from about 40% to about 70% of the theoretical influence range.

7 Conclusions

One of the main criteria which determines the designing and conducting the exploitation is the impact of the exploitation of the environment. The movement of the void to the land surface is causing the occurrence of deformations. Because of the objects protection, the size and the range of the influence are being determined. The intensity of the mining-caused damage is dependent on the mining-geological parameters of the exploitation. On the basis of the theoretical calculations, the forecasted exploitation influences as well as the influence range can be determined. When analysing the outcomes of the revealed deformations, three definitions of the influence range can be indicated:

• the theoretical influence range—the distance from the exploitation edge to the point in which deformations reach certain magnitude (assumed) or the distance in which it can be assumed that the influences are disappearing in accordance with the theoretical considerations (the model);

• the damage influence range—the distance from the exploitation edge to the point in which deformation reaches the defined border magnitudes (damaging) for the objects located on the land surface (e.g., the border magnitude of the damaging deformations for the cubature objects);

• the measurable influence range—the distance from the exploitation edge to the point in which the magnitudes of the deformations indicators are bigger than the error of the adopted measuring method with the appropriate level of trustfulness taken.

Each of these defined ranges is having the different magnitude, and each of them should be used in different situations:

• the theoretical influence range—used mainly in connection with calculating the forecasted deformation indicators in accordance with the adopted calculating method;

• the damage influence range—used primarily in designing the mining exploitation and in determining the borders of the mining areas;

• the measurable influence range—used for designing the mining measurements dedicated to monitoring the deformation influences.

In accordance with the presented considerations, it has to be stated that the furthest range is the theoretical influence one and the shortest one is the damage influence range. From the perspective of protecting the objects affected by the mining exploitation, the most optimal solution is to use the damage influence range.