Abstract
Multiscale interaction between monsoonal circulation and the local topography causes the southern front of the Darjeeling–Bhutan Himalaya to receive one of the highest annual rainfalls (3000–6000 mm) and most frequent heavy rains (up to 800 mm day−1) along the whole southern Himalayan margin. An examination of the patterns of annual rainfall, rainfall concentration, overland flow generation and slope instability indices in the Darjeeling–Bhutan Himalaya for 1986–2015 indicates that the mountain front disturbs rainfall gradient between the Bay of Bengal and the Tibetan Plateau. The results show that the precipitation concentration indices are lowest at the Himalayan front where the annual rainfall and the number of rainy days are highest. The Himalayan front has the highest predisposition to produce overland flow compared to adjacent foreland and the mountain interior. The average probability of the rainfall initialising the shallow landslides increases from 0.6% for a 1-day rainfall threshold of 144 mm to 6.1% for a 4-day rainfall threshold of 193 mm in the study area. The highest probability (up to 10%) of 2-day and longer low-intensity storms at the mountain front indicate that its area is threatened with particularly larger and deeper landslides. The multivariate regression analysis reveals statistically significant linear relationships of rainfall hazard indices with elevation and the distance to the mountain front in the mountain foreland and Himalaya, respectively. Regionally, the Darjeeling Himalaya reveals lower values of rainfall hazard indices, in comparison to the Bhutan Himalaya.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mountain ranges whose axis lies perpendicular to the prevailing wind direction disturb the vertical stratification of the atmosphere. This interaction between topography and atmospheric circulation usually results in an increase in the rainfall amount and intensity on the windward side of the mountains (Frei and Schar 1998; Wratt et al. 2000; Barros et al. 2004; Roe 2005; Bookhagen and Burbank 2006; Boers et al. 2015). Thus, mountains influence natural hazards such as landslides, erosion and floods in the short term through the control of rainfall distribution and intensity (Bookhagen and Strecker 2008; Dahal and Hasegawa 2008; Bookhagen 2010; Dimri et al. 2016). In effect, in the long term, the pattern of rainfall shapes the form of the mountain ranges (Roe et al. 2003; Thiede et al. 2005; Anders et al. 2008; Champagnac et al. 2012).
The interaction between large-scale circulation and the topography plays a crucial role in determining the rainfall pattern of the Eastern Himalaya (Anders et al. 2006; Houze et al. 2007; Murata et al. 2007; Medina et al. 2010; Goswami et al. 2010; Romatschke and Houze 2011; Prokop and Walanus 2015). These studies have revealed two general rainfall gradients in this area. Rainfall gradually decreases from E to W with the distance from the Bay of Bengal as the major moisture source and decreases from S to N leeward of orographic barriers, towards the Tibetan Plateau.
High monsoonal rainfall combined with the undergoing uplift of the Eastern Himalaya range, their deep weathered mantle and steep slopes, makes it particularly prone to landslides, generation of the surface runoff, erosion and floods. Thus, rainfall in the Darjeeling–Bhutan Himalaya region (western part of the Eastern Himalaya) has been documented with a gauge network and remote sensing techniques to investigate the relief evolution at different timescales (Starkel 1972, 2004; Starkel and Basu 2000; Baillie and Norbu 2004; Grujic et al. 2006; Soja and Starkel 2007; Starkel et al. 2008). The impact of extreme rainfall on landslides, floods and sediment delivery to the foreland was analysed, including the problem of deforestation, agriculture and settlement development (Dutt 1966; Basu and Ghatowar 1988, 1990; Froehlich et al. 1990; Starkel and Sarkar 2002; Prokop and Płoskonka 2014). Several studies on hydrometeorological aspects of floods in the Himalaya also mentioned extreme rainfall registered at individual stations in the Darjeeling–Bhutan Himalaya and their foothills (Dhar et al. 1975, 1984; Dhar and Nandargi 2000, 2003; Hofer and Messerli 2006; Nandargi and Dhar 2011). They reveal that a major rainfall event in the first Himalayan ranges or in the adjacent foothills immediately triggers flooding in the hills themselves and in their forelands.
However, all of these studies focused mainly on high annual rainfall in this area or concentrated on individual extreme events as factors of slope instability and floods. Therefore, our knowledge of the spatial and temporal rainfall distribution along the front of the Darjeeling and Bhutan Himalaya is still general and fragmentary.
The aim of this research is to quantify the impact of the mountain front on the rainfall hazard pattern. The rainfall hazard is evaluated on the basis of annual rainfall and synthetic indices with respect to precipitation concentration, overland flow generation and slope instability.
2 Materials and methods
2.1 Study area
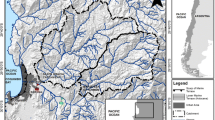
The study area is located in the Darjeeling and western part of the Bhutan Himalaya, just north of the gap between the Deccan Plateau and the Meghalaya Plateau (Fig. 1). Here, the southern front of the mountains forms the first orographic barrier for the humid south-west monsoon winds, on their way from the Bay of Bengal to the Himalaya. Therefore, it experiences one of the highest annual rainfalls (4000–6000 mm) and the most frequent heavy rains (up to 800 mm day−1) along the whole of the Himalayan front (Starkel 1972; Starkel and Basu 2000; Soja and Starkel 2007; Bookhagen 2010).
Study area (rectangle) against the background of the precipitable water (kg m−2) and wind vector (m s−1) based on the MERRA (2016) reanalysis (1986–2015)
The mountain front in the study area is very distinct and usually rises rapidly from the piedmont zone (Fig. 2; Table 1). The Himalayan edge does not have a linear structure, but retreats up to 10–15 km to the north in some sections, forming semicircular bays bordered by linear segments of tectonic origin. Thus, the real length of the Himalayan front reaches 180 km, while its relative height is 1500–2500 m high.
The southernmost frontal zone of the Darjeeling–Bhutan Himalaya is composed of unconsolidated sandstones and conglomerates of Siwaliks. This discontinuous belt, of up to 5 km wide, is bounded northward with deep weathered gneisses, shales and phyllites (Acharyya 1980; Long et al. 2011). The terrain is intensively dissected with closely spaced and incised river valleys. Among the rivers only the Tista and the Torsa originate in the glaciated High Himalaya, while Jaldhaka starts in the Lesser Himalaya. The other rivers are small and drain mountain catchments of stream order 5–6 and an area of 10–150 km2. Heavy rainfalls cause the specific runoff in these small catchments to be several times higher compared to large river catchments. This facilitates very high rates of denudation and the formation of alluvial fans at the outlet of rivers to the Himalayan piedmont (Starkel et al. 2008).
The piedmont area represents a system of fans and tectonic blocks decreasing in elevation from 200 to 500 m a.s.l. at the base of the mountain to 100 m a.s.l. over a distance of 15 km (Nakata 1972; Chakraborty and Ghosh 2010). Their surface is dissected by the braided channels of the rivers draining the Himalaya. At a distance of 15–20 km southward from the Himalayan foothills, the fans coalesce into an extensive alluvial plain, gradually lowering from 100 to 50 m a.s.l.
According to the Koppen classification, the climate is subtropical monsoonal with Cwa type in the foothills and Cwb type in the highest parts of the mountain front. About 78% of the annual rainfall occurs during the south-west monsoon between June and September. The contribution of pre-monsoon (March to May) and post-monsoon (October to December) rainfall to the annual rainfall is about 16 and 5%, respectively. However, during both of these seasons, rainstorms may occur that are associated with the local convection and tropical cyclones activity over the Bay of Bengal (India Meteorological Department 2008). For the winter months, January and February, relatively drier conditions prevail.
2.2 Data and methods
Despite long-term observations at Indian meteorological stations and tea gardens, it was found that there were long gaps prior to 1980. Also, Bhutan’s stations have relatively short periods of observations. We therefore selected stations that provide monthly and daily rainfall data, presenting relatively uniform coverage throughout the study area after 1985.
The rainfall data set of 22 stations for the period between 1986 and 2015 was obtained from the National Data Centre of the Indian Meteorological Department, Bhutan Hydrometeorological Department and tea gardens. Part of the data were also collected from printed archives and directly from the raingauge stations during extensive fieldwork in the period 2009–2015. Monthly rainfall data were available for all selected stations, while daily rainfall was available for 19 of them. Over the 30-year period, less than 10% of daily rainfall values were found to be missing. Missing daily rainfall values were filled using correlations of daily data with neighbouring stations and a dense network of tea gardens that carried out their own daily rainfall measurements. A rainy day was defined as having rainfall of at least 0.1 mm.
The Cartosat-1 Digital Elevation Model with 27 m spatial resolution (ISRO 2015) was used to delineate the range and profile of the southern Himalayan foothills. An ordinary kriging interpolation method was used as a reference for mapping spatial distribution of rainfall hazard.
In order to estimate the aggressivity (erosivity) of rainfall, the precipitation concentration index (PCI) and the concentration index (CI), designed for measuring seasonality and daily heterogeneity, respectively, were used (Oliver 1980; Martin-Vide 2004). The PCI was calculated on a monthly rainfall basis using the equation proposed by Oliver (1980):
where p i is rainfall amount of the ith month.
The PCI was estimated on an annual and seasonal scale: pre-monsoon, south-west monsoon and post-monsoon seasons. The number 100 in the formula for the annual PCI was replaced by the numbers 25 for monsoon and 33 for pre- and post-monsoon to represent the number of months in each season as a percentage of 12 months of the year (Luis et al. 2011).
This index ranges from 8.3 to 100; the first is for a uniform monthly rainfall distribution (i.e. that same amount of precipitation in each month), and the second value, we get in case of a single wet month. Also, a PCI value of 16.7 will indicate that the total precipitation was concentrated in 1/2 of the period, and a PCI value of 25 will indicate that the total precipitation occurred in 1/3 of the period. Oliver (1980) suggested that PCI values of less than 10 represent a uniform precipitation distribution or low precipitation concentration, while values between 10 and 15 indicate a moderate precipitation concentration. Values between 15 and 20 represent an irregular distribution of rainfall, while values above 20 show a strong irregularity of precipitation distribution.
The computation of the concentration index (CI) of daily rainfall was based on aggregating daily precipitation events into increasing (1 by 1 mm) categories and determining the relative contribution (as a percentage) of progressively accumulated precipitation; (Y) as a function of the accumulated percentage of rainy days (X) during Y’s occurrence. Further details on the procedure for selecting the number of rainfall classes can also be found in Martin-Vide (2004).
Y and X are related according to the law with an exponential factor as (Riehl 1949; Olascoaga 1950):
where a and b are constants estimated by least squares method.
Curve (2) is also termed as a Lorenz curve or normalised rainfall curve (Jolliffe and Hope 1996) when referring to precipitation.
The normalised daily precipitation concentration index can be defined as follows:
where S is the area delimited by the exponential curve and the line Y = X is:
where A is the definite integral of the curve (2) between 0 and 100 (the range of X values), i.e. the area under the Lorenz curve:
The value of the CI is always a number between 0 and 1. Higher precipitation concentration, represented by higher percentages of the annual total precipitation in a few very rainy days, has a greater potential to cause soil erosion and floods. The CI is useful in environmental studies whose aim is to estimate the risk of soil loss or evaluate the water resources.
The predisposition of a site to produce overland flow (P AMCIII/50) with potential erosive effects was estimated by calculating the conditional probability of occurrence of daily events with a minimum of 50 mm of rainfall, preceded by at least 28 mm during the previous 5 days (antecedent moisture conditions AMCIII) (Gold et al. 1986) modified by Gregori et al. (2006):
where \(N_{{p(50) - {\text{AMCIII}}}}^{0}\) is number of days with both rainfall ≥50 mm and AMCIII ≥28 mm; \(N_{p(50)}^{0}\), number of days with rainfall ≥50 mm over the complete observation period; \(P[p(50)]\), annual exceeding probability of the daily threshold of 50 mm.
A daily rainfall threshold of 50 mm corresponds to large storms. The rainfall amount for the previous 5 days indicates a saturation of soil (AMCIII) during the dormant vegetative season according to the curve number (CN) method (SCS-USDA 1972). The approach combines meteorological factors, which almost certainly cause the formation of runoff and water erosion regardless of vegetation cover, relief and soil conditions (Gregori et al. 2006).
Rainfall represents one of the principle factors triggering landslides. The causal relationship between rainfall and shallow landslides is the result of several factors such as rainfall amount and intensity, antecedent moisture conditions of the substrate cover and its thickness. Therefore, the probability estimation of shallow landslides estimation is more accurate when it is based on local relationships between rainfall and slope instability (Guzzetti et al. 2008).
The role of the rainfall in triggering shallow landslides was assessed using the threshold relationship fitted to the lower boundary of the field defined by landslide-triggering rainfall events for the Nepal Himalaya (Dahal and Hasegawa 2008):
where I is rainfall intensity in mm h−1; D, duration in hours.
Equation (7) reveals that when the 24-, 48-, 72- and 96-h rainfall exceeds 144, 167, 181 and 193 mm, respectively, the risk of shallow landslides on Himalayan mountain slopes is high. The rainfall thresholds are similar to that described by Froehlich et al. (1990) on the basis of field observations for the Darjeeling Himalaya. They found that shallow landslides on steep slope segments occur when 24-h rainfall reaches 130–150 mm or the continuous 3-day rainfall totals 180–200 mm in the same area.
3 Results
3.1 Distribution of annual rainfall and number of rainy days
The annual rainfall distribution pattern is strongly controlled by the southern front of the Himalaya (Figs. 3, 4). Rainfall increases from 3000 mm in the foreland at the distance of 30–40 km from the mountain front to 5000–6000 mm in the southern foothills of the Darjeeling–Bhutan Himalaya. Rainfall then decreases to below 3000 mm at stations located 15 km northward from the southern edge of the mountains. Further in the mountains, the rainfall goes down to below 1000 mm (Baillie and Norbu 2004).
Spatial distribution of the mean annual precipitation in mm (a) and the annual number of rainy days (b). Dotted line indicates foothills of the Himalayan mountain front. Map covers the area and stations presented in Fig. 2
The mountain front encompasses an approximately 8–10-km-wide belt of the Himalayan margin (the first step visible on average height profile of the Himalaya, cf. Fig. 4). The system of alluvial fans and uplifted tectonic blocks dissected by valleys with terraces causes variability of relative heights up to 400 m at the Himalayan foothills. This factor combined with the change of the mountain front course in relation to moisture-laden winds results in the highest annual rainfall at Sibsu station (Fig. 5; Table 1). In effect, the differences in annual rainfall amounts reach 27% at neighbouring stations. At the mountain front, depending on the local topography, the rainfall remains similar to that observed at the foothills or rises slightly—however, only up to approximately 1000 m a.s.l. This is evidenced by 4969 mm of annual rainfall at Buxa station located ~2 km from the foothills at 824 m a.s.l. and the Kurseong station, which notice lower annual rainfall of 3990 mm and is located 8 km from the foothills at 1476 m a.s.l. This confirms previous observations that the highest annual rainfall and major extreme 1-day rainfall are mainly reported from an altitude below 1000 m a.s.l. along the southern steep edge of Himalayan front (Starkel et al. 2008; Nandargi and Dhar 2011).
The number of rainy days to some extent follows the annual rainfall distribution (Fig. 3). In the Himalayan foreland, it increases from 112 to 140 as it approaches the mountain margin. The number of rainy days is highest at the Himalayan front; however, it varies between 140 and 187, depending on local topography. Northward at the distance of 15 km from the mountain front, it again decreases to 167 and 132 in the Bhutan Himalaya and the Darjeeling Himalaya, respectively.
3.2 Rainfall concentration
Precipitation concentration index (PCI) that is based on monthly data exhibits a different pattern from those observed for annual rainfall (Fig. 6a). Average annual PCI values range from 16.5 (high concentration) to 20.8 (very high concentration) with a coefficient variation of only 7%. PCI concentration decreases from the SW to the NE in the study area. The mountain front has medium rainfall concentration values, but its impact is poorly visible in the form of isoline disturbances along the Darjeeling–Bhutan Himalaya margin. Monsoon circulation is the most important factor influencing PCI distribution and masks the impact of topography on an annual scale (cf. Fig. 1).
Spatial distribution of the precipitation concentration index (PCI): a annual, b pre-monsoon season, c monsoon season, d post-monsoon season. Dotted line indicates foothills of the Himalayan mountain front. Maps cover the area and stations presented in Fig. 2
Seasonal distribution of PCI is highly variable in space (Fig. 6b–d). A moderate concentration of PCI values is observed during the pre-monsoon season with a decreasing gradient from SW in the foreland to NE in the mountains. It is similar to that of annual PCI distribution. For the south-west monsoon season, rainfall has a low concentration and is generally uniformly distributed. The lowest rainfall concentration is observed along the mountain front in the Indo-Bhutan Himalayan transboundary. The most irregular rainfall distribution (high to very high concentration) is in post-monsoon season. The lowest PCI values are clearly visible along the Himalayan front.
An analysis of seasonal PCI distribution shows that pre- and post-monsoon seasons with the highest irregularity have the largest impact on annual PCI pattern. This is related to both mesoscale circulation with the onset and withdrawal of monsoons in these seasons as well as to vigorous convective processes and cyclone activity. In addition to monsoonal rainfall during June to September, there is considerable thunderstorm activity in May in the Eastern Himalayan region, and the rainfall caused by these thunderstorms is comparable in magnitude to the rainfall of any of the monsoon months (Nandargi and Dhar 2011). Extreme rainfalls that contribute a large amount of rain are also mentioned in the literature for the post-monsoon season for this region (Abbi et al. 1970; Starkel 1972). They are frequently related to tropical cyclones moving from the Bay of Bengal towards the Himalayan orographic barrier. Such heavy rain over the Darjeeling–Bhutan Himalaya was 2–5 October 1968, when 1091, 607 and 796 mm of rainfall was noted in Kurseong, Darjeeling and Kalimpong, respectively. Rainfall amounts exceeded 200 mm several times at these stations, also in October, for 1986–2015, while average rainfall is below 100 mm in this month.
The average annual concentration index (CI) value is 0.59 in the study area (Fig. 7; Table 2). CI values exhibit less variability CV = 4%, compared to the other rainfall hazard indices. One of the lowest values (0.53–0.60) is observed along the Himalayan front. This result reveals that the CI values are noticeably lower in places where both annual rainfall and the annual number of rainy days are higher. The south-west monsoon winds deliver moisture-laden air, and much of the rainfall occurs at almost vertical scarp of the Himalaya in frequent, brief, low-intensity orographic showers. Thus, the mountain front also has the lowest percentage of rainfall, contributed by 25% of the rainiest days—usually below 70% (Table 2). In the mountains, stations located on the summits such as Darjeeling and Kalimpong receive more regular rainfall (CI = 0.56–0.57) compared to stations located in the rain shadow of mountain valleys such as Dorokha and Tendu (CI = 0.60–0.61), regardless of the altitude.
Spatial distribution of the normalised daily precipitation concentration index (PCI). Dotted line indicates foothills of the Himalayan mountain front. Map covers the area and stations presented in Fig. 2
The foreland of the Darjeeling–Bhutan Himalaya recorded high CI values of above 0.60, indicating that above 70% of total rainfalls on 25% of the rainiest days. The high concentration can be related to irregular ‘break monsoon periods’, i.e. the shifting of the eastern end of the seasonal monsoon trough to the foothills of the Himalayas in the north, when the monsoon activities are intensified (Maharana and Dimri 2015). The study of Dhar et al. (1984) has shown that, on a ‘break’ day, positive percentage departures of rainfall as high as 100–300% have occurred at stations located in the outer Himalaya and the adjoining plains of north Bengal. Many of the stations in the Darjeeling–Bhutan Himalayan foreland (Nagrakata, Neora, Hasimara) recorded the highest 24-h rainfall of the magnitude ~800 mm during monsoon season. This is a value similar to those observed in the Himalayan foothills and higher than those registered in the mountains (Nandargi and Dhar 2011). Moreover, it was also found that convective heating associated with the synoptic events interacts with the Eastern Himalayas and generates southward-propagating gravity waves with a period of about 24 h in north-east India (Goswami et al. 2010). The strong updrafts associated with these waves produce deep convection and heavy rainfall, especially at stations located in the Himalayan foreland.
The exponential curves of a given type in Eq. (5) were calculated for 19 analysed meteorological stations. The three curves representing the lowest, moderate and highest rainfall concentration are presented in Fig. 8. As the total area between the straight diagonal line and the concentration curve increases, the value of the CI also increases. Jalpaiguri station, in the foreland located 43 km south to the mountain front, recorded the highest CI value, with an average of 0.63. These values mean that 25% of the rainiest days contributes almost 73% of the total rain. The Darjeeling station in the Himalaya located 25 km north of the mountain front has a moderate CI value of 0.57; 25% of the rainiest days contributes almost 69% of the total rain. The lowest CI values were recorded in the Himalayan foothills at Samtse, which contributed less than 64% of the total rain based on the CI value of 0.53.
The synthetic indexes of rainfall aggressiveness allow a comparison of different sites in terms of occurrence of rainfalls with morphogenetic impact (Gregori et al. 2006). The annual concentration of precipitation PCI exhibits increasing concentration from the South China Sea coast (PCI < 15) towards the Tibet region (PCI > 30) with similar values in Yunnan Province, located relatively close to our study area (Shi et al. 2015). The CI values show a similar distribution with a lower concentration over the mountains compared to coasts than those found for the Malaysia (0.42–0.61) and the South China (0.46–0.68) in tropical monsoonal and subtropical monsoonal climates, respectively (Suhaila and Jemain 2012; Huang et al. 2013; Shi et al. 2015).
3.3 Overland flow occurrence probability
Average annual overland flow occurrence probability (P AMCIII/50) is 5.1% with a coefficient of variation 30%. The impact of topography is one of the most clearly visible among the analysed rainfall hazard indices. The mountain front has the highest probabilities of overland flow events above 5.0% (Fig. 9). This zone has two centres where the probability reaches 8–9%, located in the transboundary of the Darjeeling–Bhutan Himalaya and the Bhutan Himalaya itself. The high overland flow occurrence probability is an effect of frequent daily rainfalls that pass a 50 mm threshold as well as a high number of rainy days, reaching 23–27 in every month between June and September. The combination of these two factors maintains the moist condition of the soil throughout the monsoon season. In the mountain interior, 15 km from the southern foothills of the Himalaya, the runoff probability decreases to 2–3%, and is by half, smaller than in the foreland.
Spatial distribution of the overland flow probability P AMCIII/50. Dotted line indicates foothills of the Himalayan mountain front. Map covers the area and stations presented in Fig. 2
Runoff frequently occurs in association with the same type of intense rainstorms that cause flash flooding. High rainfall intensity and saturation of the soil profile combined with a dense river network, direct contact of steep slopes and river channels facilitate rapid flood generation and enormous sediment load in the Darjeeling–Bhutan Himalaya (Starkel and Basu 2000). The specific discharge and specific sediment yields are up to several dozen times higher in Siwaliks compared to the Higher Himalaya (Ives 2004; Hofer and Messerli 2006; Starkel et al. 2008). Their impact is not limited to the first Himalayan ranges, but the fluxes of water and sediment have a strong influence on their piedmont.
3.4 Shallow landslide-triggering probability
The probability of the rainfall initialising the landslides rises and differentiates spatially, together with the rainfall duration. The average probability of daily rainfall of 144 mm is 0.6% and ranges between 0.2 and 1.4%. The probability is highly variable (CV = 50%) in the study area with no visible impact of landform on spatial distribution of rainfall threshold (Fig. 10). This indicates that the high 1-day rainfall intensities are rather randomly localised. The average probability of the 2-day rainfall reaches 2.4%. Its coefficient of variation decreases to 35%. The differentiation between the foreland and mountains is more distinct as well as between the Darjeeling and the Bhutan Himalaya. The average probability of the 3- and 4-day rainfall rises to 4.3% and 6.1%, respectively. The coefficient of variation also drops to below 30% in both cases. The influence of the topography on the rainfall threshold distribution is clearly visible. The highest probability is within the mountain front up to 10.0%, while the lowest is in the Himalayan interior, 2–4%. Probability is also twice as high in the Bhutan Himalaya compared to the Darjeeling Himalaya.
Spatial distribution of the landslide-triggering probability (%) for 1, 2, 3 and 4 days of 144 mm (a), 167 mm (b), 181 mm (c) and 193 mm (d) of rainfall, respectively. Dotted line indicates foothills of the Himalayan mountain front. Map covers the area and stations presented in Fig. 2
The Himalayan rainfall threshold (Dahal and Hasegawa 2008) resembles that which was proposed for that humid tropical climate of Puerto Rico (Larsen and Simon 1993), but with a slightly lower threshold value. Short but high-intensity storms may trigger mostly small and shallow landslides in unconsolidated material. Larsen and Simon (1993) argue that these landslides had failure planes in saprolite or at the soil–saprolite boundary. In contrast, storms of long duration but low intensity (i.e. 72 h and longer) have triggered the larger and deeper landslides. In this case, prolonged water infiltration permits excess pore pressure more deeply, between the saprolite and unweathered bedrock boundary.
The role of the antecedent rainfall in triggering landslides is more complicated. Dahal and Hasegawa (2008) suggested that a moderate correlation exists between the antecedent rainfalls of 3–10 days and the daily rainfall at failure in the Nepal Himalaya. Larsen and Simon (1993) stated that antecedent rainfalls play an important role in the temperate climate, but its effect in a humid climate is negligible because frequent rainfall keeps the soil in wet conditions throughout the year. In our case, the antecedent rainfall plays probably a minor role during monsoon season because there are only a few days without rainfall. However, the role of antecedent rainfall can be important in the post-monsoon season when soil moisture is increased following the four wettest months of the year.
3.5 Impact of topographic variables on rainfall hazard
Interpolation considers spatial relationships among sampling points and does not take into account other properties of the landscape. In the mountains, the impact of topographic variables such as altitude or slope orientation on rainfall is very important. Our study area shows two clearly differentiated landscape units: gently inclined foreland and mountains with rugged topography. The contrasting areas led us to select two independent topographic variables: distance to mountain front (i.e. Himalayan foothills) and altitude as predictors of spatial rainfall and synthetic indices distribution. The relationships were derived through multivariate regression. An adjusted determination coefficient (R 2) was also calculated, which compensates for this optimistic trait in the determination coefficient, by taking into account the size of the sample and the number of prediction variables.
The calculated relationships between rainfall and the independent topographic variables fit linear models (Table 3). The regression approach using two topographic variables (distance to the mountain front and elevation) enabled us to describe 61–67% of the spatial variability of annual rainfall, 55–65% predisposition of a site to produce overland flow, as well as 54–62% of a 2-, 3- and 4-day rainfall threshold, triggering shallow landslides in the mountains.
In the foreland, the annual rainfall, concentration indices and overland flow occurrence probability models are statistically significant at α < 0.05 level. In the mountains, the annual rainfall, overland flow occurrence probability as well as 2-, 3- and 4-day rainfall thresholds models are statistically significant at the same level. Only a 1-day rainfall threshold model for triggering landslides is not statistically significant in either landscape units. The analysis using multivariate regression reveals that elevation is a more statistically significant topographic variable in the foreland, while distance to the mountain front (Himalayan foothills) is more important in the mountains.
4 Conclusions
Examination of the spatial distribution of annual rainfall and rainfall hazard indices in the Darjeeling–Bhutan Himalaya indicates that the mountain front disturbs described earlier rainfall gradient between the Bay of Bengal and the Tibetan Plateau. The same type of intense or prolonged rainstorms can simultaneously initiate several processes such as runoff, soil erosion, flood, debris flow and landslides. The area most threatened by the effects of these processes extends from the Himalayan foothills up to 1000 m a.s.l., which has a width of about 8–10 km towards the mountain interior. This zone of mountain front has the highest rainfall accompanied with its lowest concentration, the highest probability of runoff occurrence as well as 2-, 3- and 4-day rainfall initiating landslides, compared to adjacent foreland and the mountain interior. A high frequency of long-duration and low-intensity storms indicates that the mountain front is threatened particularly by larger and deeper landslides.
However, the mountain front is not homogenous in terms of rainfall hazard. A combination of two factors—variability of relative heights and changes of the mountain front course in relation to moisture-laden winds—causes differences of annual rainfall at neighbouring stations to reach 27%. These differences are enhanced in case of annual rainfall hazard indices up to 43%.
The analysis of rainfall hazard indices demonstrated their different spatial behaviour between foreland and Himalaya. The multivariate regression approach reveals statistically significant linear relationships of rainfall hazard indices with elevation in the Himalayan foreland. In contrast, higher dependency of rainfall hazard indices on distance from the mountain front is visible in the Himalaya. Therefore, adiabatic cooling and heavy rainfall at the southern Himalayan orographic barrier strengthens decrease in rainfall in the mountain interior.
In comparison to the Bhutan Himalaya, the Darjeeling Himalaya reveals lower indices of daily rainfall concentration, predisposition to overland flow and probability of triggering landslides for a 2-day and longer rainfall duration. Thus, catastrophic effects of erosion, landslides and floods in the Darjeeling Himalaya, frequently described in literature, are more related to intensive human activity such as the development of settlements, agriculture, road and reservoirs construction, than to rainfall hazards only.
References
Abbi SDS, Gupta DK, Jain BC (1970) A study of heavy rainstorms over North Bengal. Indian J Meteorol Geophys (Mausam) 21(2):195–210
Acharyya SK (1980) Structural framework and tectonic evolution of the Eastern Himalaya. Himal Geol 10:412–439
Anders AM, Roe GH, Halle B, Montgomery DR, Finnegan NJ, Putkonen J (2006) Spatial patterns of precipitation and topography in the Himalaya. Geol Soc Am Spec Pap 398:39–53. doi:10.1130/2006.2398(03)
Anders AM, Roe GH, Montgomery DR, Hallet B (2008) Influence of precipitation phase on the form of mountain ranges. Geology 36(6):479–482
Baillie IC, Norbu C (2004) Climate and other factors in the development of river and interfluve profiles in Bhutan, Eastern Himalayas. J Asian Earth Sci 22(5):539–553. doi:10.1016/S1367-9120(03)00092-0
Barros AP, Kim G, Williams E, Nesbitt SW (2004) Probing orographic controls in the Himalayas during the monsoon using satellite imagery. Nat Hazard Earth Syst 4(1):29–51
Basu SR, Ghatowar L (1988) Landslides and soil-erosion in the Gish drainage basin of the Darjeeling Himalaya and their bearing on North Bengal floods. Studia Geom Carpato Balc 22:105–122
Basu SR, Ghatowar L (1990) The impact of landslides on fluvial processes in the Lish basin of the Darjeeling Himalayas. Geogr Pol 59:77–87
Boers N, Bookhagen B, Marwan N, Kurths J (2015) Spatiotemporal characteristics and synchronization of extreme rainfall in South America with focus on the Andes Mountain range. Clim Dyn 46:601–617. doi:10.1007/s00382-015-2601-6
Bookhagen B (2010) Appearance of extreme monsoonal rainfall events and their impact on erosion in the Himalaya Geomat. Nat Hazard Risk 1(1):37–50. doi:10.1080/19475701003625737
Bookhagen B, Burbank DW (2006) Topography, relief, and TRMM-derived rainfall variations along the Himalaya. Geophys Res Lett. doi:10.1029/2006GL026037
Bookhagen B, Strecker MR (2008) Orographic barriers, high resolution TRMM rainfall, and relief variations along the eastern Andes. Geophys Res Lett 35:1–6. doi:10.1029/2007GL032011
Chakraborty T, Ghosh P (2010) The geomorphology and sedimentology of the Tista megafan, Darjeeling Himalaya: implications for megafan building processes. Geomorphology 115:252–266. doi:10.1016/j.geomorph.2009.06.035
Champagnac JD, Molnar P, Sue C, Herman F (2012) Tectonics, climate, and mountain topography. J Geophys Res Solid Earth. doi:10.1029/2011JB008348
Dahal RK, Hasegawa S (2008) Representative rainfall thresholds for landslides in the Nepal Himalaya. Geomorphology 100:429–443. doi:10.1016/j.geomorph.2008.01.014
Dhar ON, Nandargi S (2000) A study of floods in the Brahmaputra basin in India. Int J Climatol 20:771–778
Dhar ON, Nandargi S (2003) Hydrometeorological aspects of floods in India. Nat Hazards 28(1):1–33
Dhar ON, Kulkarni AK, Sangam RB (1975) study of extreme point rainfall over flash flood prone regions of the Himalayan foothills of North India. Hydrol Sci Bull 20:61–67
Dhar ON, Soman MK, Mulye SS (1984) Rainfall over the southern slopes of the Himalayas and the adjoining plains during ‘breaks’ in the monsoon. J Climatol 4(6):671–676
Dimri AP, Thayyen RJ, Kibler K, Stanton A, Jain SK, Tullos D, Singh VP (2016) A review of atmospheric and land surface processes with emphasis on flood generation in the Southern Himalayan rivers. Sci Total Environ 556:98–115. doi:10.1016/j.scitotenv.2016.02.206
Dutt GN (1966) Landslides and soil erosion in the Kalimpong Subdivision, Darjeeling district and their bearing on the North Bengal Flood. Bull Geol Surv India B 15:62–69
Frei C, Schar C (1998) A precipitation climatology of the Alps from high-resolution raingauge observations. Int J Climatol 18:873–900
Froehlich W, Gil E, Kasza I, Starkel L (1990) Thresholds in the transformation of slopes and river channels in the Darjeeling Himalaya, India. Mt Res Dev 10:301–312
Gold AJ, Loudon TL, Nurnberger FV (1986) Runoff and erosive storm occurrence probabilities. Trans ASAE 29(1):119–123
Goswami BB, Mukhopadhyay P, Mahanta R, Goswami BN (2010) Multiscale interaction with topography and extreme rainfall events in the northeast Indian region. J Geophys Res Atmos. doi:10.1029/2009JD012275
Gregori E, Costanza M, Zorn G (2006) Assessment and classification of climatic aggressiveness with regard to slope instability phenomena connected to hydrological and morphological processes. J Hydrol 329:489–499
Grujic D, Coutand J, Bookhagen B, Bonnet S, Blythe A, Duncan Ch (2006) Climatic forcing of erosion, landscape and tectonics in the Bhutan Himalaya. Geology 34:801–804. doi:10.1130/G22648.1
Guzzetti F, Peruccacci S, Rossi M, Stark CP (2008) The rainfall intensity–duration control of shallow landslides and debris flows: an update. Landslides 5(1):3–17. doi:10.1016/j.jhydrol.2006.03.001
Hofer T, Messerli B (2006) Floods in Bangladesh: history, dynamics and rethinking the role of the Himalayas. United Nations University Press, Tokyo
Houze RA, Darren CW, Bradley FS (2007) Monsoon convection in the Himalayan region as seen by the TRMM Precipitation Radar. Q J R Meteorol Soc 133:1389–1411. doi:10.1002/qj.106
Huang J, Sun S, Zhang J (2013) Detection of trends in precipitation during 1960–2008 in Jiangxi province, southeast China. Theor Appl Climatol 114(1–2):237–251. doi:10.1007/s00704-013-0831-2
India Meteorological Department (2008) Tracks of storms and depressions in the Bay of Bengal and theArabian Sea 1877–1970. Cyclone eAtlas—IMD. Regional Meteorological Centre, Chennai
ISRO (Indian Space Research Organization) (2015) Cartosat-1 Digital Elevation Model. http://bhuvan.nrsc.gov.in. Accessed 10 March 2016
Ives JD (2004) Himalayan perceptions: Environmental change and the well-being of mountain peoples. Routledge, London
Jolliffe IT, Hope PB (1996) Representation of daily rainfall distributions using normalized rainfall curves. Int J Climatol 16:1157–1163
Larsen MC, Simon A (1993) A rainfall intensity-duration threshold for landslides in a humid-tropical environment, Puerto Rico. Geogr Ann 75A(1–2):13–23
Long S, McQuarrie N, Tobgay T, Grujic D, Hollister L (2011) Geologic map of Bhutan. J Maps. doi:10.4113/jom.2011.1159
Luis MD, Gonzalez-Hidalgo JC, Brunetti M, Longares LA (2011) Precipitation concentration changes in Spain 1946–2005. Nat Hazard Earth Syst 11(5):1259–1265. doi:10.5194/nhess-11-1259-2011
Maharana P, Dimri AP (2015) Study of intraseasonal variability of Indian summer monsoon using a regional climate model. Clim Dyn 46:1043–1064. doi:10.1007/s00382-015-2631-0
Martin-Vide J (2004) Spatial distribution of a daily precipitation concentration index in peninsular Spain. Int J Climatol 24:959–971. doi:10.1002/joc.1030
Medina S, Houze RA, Kumar A, Niyogi D (2010) Summer monsoon convection in the Himalayan region: terrain and land cover effects. Q J R Meteorol Soc 136:593–616. doi:10.1002/qj.601
MERRA (The Modern-Era Retrospective analysis for Research and Applications) (2016) Global Modeling and Assimilation Office Goddard Space Flight Center, NASA. http://giovanni.gsfc.nasa.gov/giovanni/. Accessed 10 May 2016
Murata F, Hayashi T, Matsumoto J, Asada H (2007) Rainfall on the Meghalaya plateau in northeastern India—one of the rainiest places in the world. Nat Hazards 42(2):391–399. doi:10.1007/s11069-006-9084-z
Nakata T (1972) Geomorphic history and crustal movements of the foot-hills of the Himalayas. The scientific reports of the Tohoku University 7th Series. Geography 22:39–177
Nandargi S, Dhar ON (2011) Extreme rainfall events over the Himalayas between 1871 and 2007. Hydrol Sci J 56(6):930–945. doi:10.1080/02626667.2011.595373
Olascoaga MJ (1950) Some aspects of Argentine rainfall. Tellus 2:312–318
Oliver JE (1980) Monthly precipitation distribution: a comparative index. Prof Geogr 32:300–309
Prokop P, Płoskonka D (2014) Natural and human impact on the land use and soil properties of the Sikkim Himalayas piedmont in India. J Environ Manag 138:15–23. doi:10.1016/j.jenvman.2014.01.034
Prokop P, Walanus A (2015) Variation in the orographic extreme rain events over the Meghalaya Hills in northeast India in the two halves of the twentieth century. Theor Appl Climatol 121(1–2):389–399. doi:10.1007/s00704-014-1224-x
Riehl H (1949) Some aspects of Hawaiian rainfall. Bull Am Meteorol Soc 3:176–187
Roe GH (2005) Orographic precipitation. Annu Rev Earth Planet Sci 33:645–671. doi:10.1146/annurev.earth.33.092203.122541
Roe GH, Montgomery DR, Hallet B (2003) Orographic precipitation and the relief of mountain ranges. J Geophys Res Solid Earth. doi:10.1029/2001JB001521
Romatschke U, Houze RAJ (2011) Characteristics of precipitating convective systems in the premonsoon season of South Asia. J Hydromet 12:157–180. doi:10.1175/2010JHM1311.1
SCS-USDA (1972) Hydrology National Engineering Handbook. Sect.4. Washington, DC
Shi P, Wu M, Qu S, Jiang P, Qiao X, Chen X, Zhou M, Zhang Z (2015) Spatial distribution and temporal trends in precipitation concentration indices for the southwest China. Water Resour Manag 29(11):3941–3955. doi:10.1007/s11269-015-1038-3
Soja R, Starkel L (2007) Extreme rainfalls in Eastern Himalaya and southern slope of Meghalaya Plateau and their geomorphologic impacts. Geomorphology 84(3):170–180. doi:10.1016/j.geomorph.2006.01.040
Starkel L (1972) The role of catastrophic rainfall in the shaping of the relief of the Lower Himalaya (Darjeeling Hills). Geogr Polonica 21:103–147
Starkel L (2004) Temporal clustering of extreme rainfall events in relief transformation. J Geol Soc India 64:517–523
Starkel L, Basu S (eds) (2000) Rains, landslides, and floods in the Darjeeling Himalaya. INSA, New Delhi
Starkel L, Sarkar S (2002) Different frequency of threshold rainfalls transforming the margin of Sikkimese and Bhutanese Himalaya. Studia Geomor Carpat Balc 36:51–67
Starkel L, Sarkar S, Soja R, Prokop P (2008) Present-day evolution of the Sikkimese-Bhutanese Himalayan piedmont. Prace Geograficzne 219. IGiPZ PAN, Warszawa
Suhaila J, Jemain AA (2012) Spatial analysis of daily rainfall intensity and concentration index in Peninsular Malaysia. Theor Appl Climatol 108(1–2):235–245. doi:10.1007/s00704-011-0529-2
Thiede RC, Arrowsmith JR, Bookhagen B, McWilliams MO, Sobel ER, Strecker MR (2005) From tectonically to erosionally controlled development of the Himalayan orogen. Geology 33(8):689–692. doi:10.1130/G21483.1
Wratt DS, Revell MJ, Sinclair MR, Gray WR, Henderson RD, Chater AM (2000) Relationships between air mass properties and mesoscale rainfall in New Zealand’s Southern Alps. Atmos Res 52:261–282. doi:10.1016/S0169-8095(99)00038-1
Acknowledgements
This paper is the outcome of research Project No. 2012/05/B/ST10/00309 of the National Science Centre (Poland) in cooperation with the Indian National Science Academy.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Prokop, P., Walanus, A. Impact of the Darjeeling–Bhutan Himalayan front on rainfall hazard pattern. Nat Hazards 89, 387–404 (2017). https://doi.org/10.1007/s11069-017-2970-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-017-2970-8