1 Introduction

Tsunami fragility curves for buildings provide a probabilistic link between a tsunami intensity measure (TIM) and building damage. They are a component of tsunami risk models, and so are vital for land use and emergency planning, as well as human and financial loss estimation.

Compared to seismic studies, few fragility curves for buildings affected by tsunami exist, and to date, almost all have been derived based solely on empirical data (post-tsunami building damage surveys). However, the applicability of empirical tsunami fragility curves for buildings is limited by the availability and quality of data from past events. Until the 2011 Great East Japan earthquake and tsunami (2011 GEJE) no fragility curves existed for engineered buildings. Furthermore, tsunami fragility curves were based on aggregated empirical datasets where building damage statistics for a number of different geographical areas (of small or large size) are combined, with each such area assumed to be associated with a single TIM value (for example, Peiris (2006) constructs curves using data from the entire SW and SE coasts of Sri Lanka). Even in cases where disaggregated data are available researchers have at times aggregated the damage observations over areas with similar TIM values, e.g. Suppasri et al. (2012a, b). The vast majority of existing fragility curves are determined from aggregated empirical data using linear regression models and ordinary least squares (OLS) parameter estimation. However, Charvet et al. (2014a, b) and Rossetto et al. (2014) show that OLS regression in these cases is not theoretically correct as several of the linear model assumptions are violated by the data. For example, OLS regression assumes that errors are normally distributed, when in fact damage data are binary (damaged/not damaged), or ordinal (falling into one of several damage state categories). Charvet et al. (2014a, b) postulate that generalised linear models (GLMs) should provide an improvement over OLS for deriving fragility curves, as they allow for a relaxation of some of the assumptions, but do not compare the results of using this statistical model fitting approach to more complex nonparametric alternatives. Furthermore, no existing study has quantifiably assessed the effects of data aggregation and OLS linear model assumption violation on model predictive power.

The intensity measure (independent variable) represented in a fragility curve should provide the best possible representation of the damage potential of the tsunami inundation. Tsunami-induced building damage can arise due to hydrostatic forces (including buoyancy), hydrodynamic effects (drag and bore impact) and debris (impact and damming). The severity of these effects are determined by a number of flow parameters, yet the majority of existing tsunami fragility curves adopt only the local maximum inundation depth as the TIM, often because it can be estimated from post-tsunami reconnaissance of buildings (Suppasri et al. 2012a, b) and also from numerical modelling of tsunami inundation. Other parameters of the flow can also be derived from inundation modelling, however withy potentially less reliability, (depending on the numerical code used, its validation and the refinement in grid size), and less opportunity to validate against observations. Velocity and hydrodynamic force (approximated by the standard form drag equation) have been used as TIMs in some recent studies (e.g. Koshimura et al. 2009; Charvet et al. 2014a, b). Tanaka and Kondo (2015) consider momentum flux (an indicator of drag force) and moment of momentum flux (the product of momentum flux and inundation depth, thought to be a proxy for the overturning moment induced by the flow) in deriving their fragility curves. They further recommend using different fragility curves for flow conditions characterised by high and low Froude numbers (a measure of flow velocity non-dimensionalised by the gravity wave velocity, indicating the flow regime such that Fr < 1 indicates sub-critical flow and Fr > 1 indicates choked flow). Overall, these studies do not show a consensus as to which flow parameter is the most appropriate TIM to estimate fragility.

There are no existing studies that adopt a rigorous approach to quantifiably compare the TIMs used and many consider only one damage state (i.e. collapse) in their assessments. Furthermore, all force estimations considered in previous studies have been based on the standard form drag equation. However, this does not account for alternative estimations such as equivalent hydrostatic methods (MLIT 2011), bore impact (Robertson and Riggs 2011) or changes in flow regime (Qi et al. 2014). Park et al. (2014) compare damage estimates for a case study town in the USA using fragility functions for depth, velocity and momentum flux, concluding that velocity and momentum flux provide the most realistic damage estimates, though this is only based on a qualitative visual assessment of damage locations and the authors acknowledge that this conclusion must be verified with field data.

In fluvial flood modelling, Kreibich et al. (2009) compare flood intensity measures (FIMs) of depth, velocity, momentum flux and energy head according to the Bernoulli equation. FIMs are compared using Spearman’s rho correlation coefficients on a dataset of 256 buildings across 5 damage states. They concluded that fluvial flooding depth and energy head have the strongest correlation with observed damage, and momentum flux has a weak correlation and flow velocity has no correlation, although it is acknowledged that a much larger sample size is required in order to draw conclusive results.

A number of seismic studies have compared seismic intensity measures (IMs) using the criteria of “efficiency” [the level of uncertainty in structural response conditional on the IM value (Luco and Cornell 2007)], “sufficiency” [the ability of the IM to describe structural response independently of other IMs or hazard characteristics (Ebrahimian et al. 2015)] and “computability” (the ease of calculating the IM value, e.g. Giovenale et al. 2004). Minas et al. (2014) compared the efficiency of multiple seismic IMs in an analytical study whereby numerical analysis was used to estimate structural response, in terms of continuous engineering demand parameters (EDP), to a range of IM levels. In the latter, efficiency was determined by using OLS parameter estimation to fit a power law relationship for each IM (\({\text{EDP}} = \beta_{0} {\text{IM}}^{{\beta_{1} }}\), where β 0 and β 1 denote the model parameters) and comparing the standard error of the residuals. However, for empirical studies, using real observed damage data, structural response is denoted by discrete damage states, and so it is not appropriate to fit a direct relationship between IM and damage state, but instead to the probability of exceedance for each damage state (i.e. fragility curves). However, to date no existing study has compared efficiency of multiple TIMs based on empirical fragility curves fit to observed damage data.

This paper collates, compares and expands on the current state-of-the-art methodologies for tsunami fragility assessment, in order to present a proposed methodology, with a case study and results, for the selection of the optimal TIM for fragility function derivation for a given dataset. Section 2 outlines the proposed methodology, broken into the following three steps: (1) explore the data and eliminate biases due to incomplete data entries using a multiple imputations approach; (2) select appropriate statistical models for TIM comparison and use these models to conduct further exploratory analysis; and (3) compare fragility curves derived for a series of different TIMs using cross-validation techniques and semi-parametric regression methods in order to identify which TIM provides the best representation of the observed damage data. Section 3 presents a unique, detailed, disaggregated, case study damage dataset from the 2011 GEJE, and an accompanying simulation of the 2011 GEJE inundation generating several flow parameters to be considered as TIMs. Each stage of the proposed methodology is then demonstrated on this case study dataset in Sect. 4, showing that the use of data aggregation and linear models utilising OLS parameter estimation is inappropriate for fragility function derivation, and identifying the optimum TIM for describing observed damage for buildings of engineered and non-engineered construction materials for the case study locations. Fragility surfaces are not considered as they are not currently widely used in practice; however, multiple inundation parameters are represented in single, more complex TIMs allowing multiple inundation parameters to be represented in a single curve. Finally, recommendations are provided in Sect. 5.

With the introduction of several concepts novel to the field of fragility assessment (MI, GAMs, KFCV for model optimisation/comparison), this study has significant implications for the future generation of empirical and analytical fragility functions.

2 Proposed methodology

A methodology is developed here which uses post-tsunami data in order to identify the optimum measure of tsunami intensity for the construction of tsunami empirical fragility curves. The methodology consists of three steps. In the first step, an exploratory analysis identifies the response and explanatory variables and assesses the quality of the database, using appropriate statistical techniques to improve it. In the second step, statistical models are selected with which to conduct the TIM comparison, and these models are used to supplement the exploratory analysis of Step 1. In the third step, the goodness of fit of each model is assessed and the TIM which fits the data best is identified. The three steps are outlined in Fig. 1, described in more detail in what follows and demonstrated for a case study dataset in Sect. 4.

Fig. 1
figure 1

Methodology flow chart with expected outputs at each Step

Full size image

Step 1: Exploratory analysis of data quality

The aim of Step 1 is to identify the response and explanatory variables from the information available in the database and to identify and treat any underlying bias. This is achieved in two stages:

  1. 1.

    Identify and assess the following categories of variables:

    1. a.

      Building construction variables.

    2. b.

      Response variable: Damage state definitions and distributions.

    3. c.

      Inundation variables: Identify and validate TIMs.

  2. 2.

    Classify and treat incomplete data entries.

The reliability of fragility functions depends on the quality of underlying the data on which they are derived. A post-tsunami database typically contains information regarding the structural characteristics of buildings, the damage that these buildings sustained (defined in terms of a response variable) as well as the tsunami intensity level (defined in terms of explanatory variables) at the location of these buildings. In order for derived fragility functions to be representative of the different structural responses to tsunami loading, buildings should be classified according to structural properties. Suppasri et al. (2014) consider structural material, height, occupancy and date of construction, but all other existing tsunami fragility studies consider structural material only, and building classifications are not consistent between studies. Therefore, it is recommended to consider what building information available can be used to categorise buildings according to their structural performance.

The response variable for empirical fragility assessment will generally be the observed damage state. McCullagh and Nelder (1989) state that damage scales for fragility analysis must be such that (1) levels of response are mutually exclusive and (2) each new response should correspond to an increase in tsunami intensity. Therefore, it is recommended to consider whether the damage scale follows these rules, and adjust the scale accordingly if not.

Inundation information can be obtained by observation or simulation, with potential errors and bias associated with both. Therefore, it is recommended that inundation information be validated and errors quantified where possible. These considerations are discussed in the global earthquake model (GEM) guidelines for empirical fragility function assessment (Rossetto et al. 2014) and are demonstrated for the case study database in Sect. 4 of this paper.

Having identified the main variables necessary for a meaningful empirical fragility assessment, the completeness of the database is then assessed, which is critical for the reliability of the constructed fragility curves. Existing studies (e.g. Suppasri et al. 2013) generally conduct complete-case analysis, i.e. they remove any partial data, such as buildings of unknown material, from their fragility analysis. However, this may lead to a loss of statistical power, loss of precision and introduction of bias if the missing data are informative. The proposed methodology uses rigorous techniques to classify missing data and complete the database accordingly.

Missing data can be assigned to one of three categories (Ware et al. (2012): missing completely at random (MCAR), missing at random (MAR), or missing not at random (MNAR) (Table 1). MCAR refers to the case where the data are missing purely by chance, in which case complete-case analysis may be conducted without introducing bias in the results. MNAR refers to the case where the missing information is related to the reason that the information is missing (e.g. if wooden buildings had been removed from the dataset because they were wooden), in which case complete-case analysis would introduce bias and missing data cannot be estimated, and so the dataset must be supplemented with additional information to address this issue before fragility analysis can be conducted. MAR refers to the case where the information is not missing completely at random but can be accounted for by using other attributes, in which case the missing data may be estimated by multiple imputation (MI) techniques. MI involves replacing missing observed data with substituted values estimated multiple times via stochastic regression models built on the other attributes (used as explanatory variables), with all of the imputations being combined in order to derive the final estimate (Rubin 1987). MI is demonstrated for the case study dataset in Sect. 4.1.2.

Table 1 Classification and treatment of missing data
Full size table

Step 2: Statistical model selection and trend analysis

The aim of Step 2 is to select appropriate models with which to conduct the TIM comparison of Step 3, and to use these models to supplement the exploratory analysis of Step 1. The outcome of Step 2 is to have selected at least two models and their optimum configurations, and to have a complete dataset with biases addressed. Step 2 therefore consists of the following stages:

  1. 1.

    Select two statistical model types via the following procedure:

    1. a.

      Select the TIM which is estimated to have the lowest error.

    2. b.

      Select two of the models in Table 2, and fit each of the configuration options for the selected TIM.

      Table 2 Statistical model types and model comparisons considered for TIM comparison
      Full size table
    3. c.

      Determine the optimum configuration options using the tests outlined in Table 2.

  2. 2.

    Use these models to conduct further exploratory analysis and sensitivity analyses:

    1. a.

      Determine the optimum construction type categories.

    2. b.

      Determine fragility function sensitivity to explanatory variable error.

    3. c.

      Determine fragility function sensitivity to missing data treatment.

It is recommended that Step 2 is conducted for the single TIM that is estimated to have the lowest error (e.g. for a particular dataset observational data may be deemed more reliable than simulation data, and inundation depth may be considered to have been measured more accurately than velocity). Given that this study concentrates on the identification of the most efficient TIM, it is necessary to select at least two statistical models to be used in Step 3 in order to draw conclusions that are not conditioned on a given statistical model. The GEM guidelines (Rossetto et al. 2014) propose three classes of statistical model: parametric, semi-parametric and nonparametric. Table 2 summarises these model classes, their configuration options (e.g. whether to fit to the TIM directly or a transform of the TIM, such as ln|TIM|) and the methods used to determine the optimum configuration. A presentation of the suitable models and their configuration options is given in the text that follows. It is recommended to select a parametric model (e.g. GLM) and then a semi-parametric or nonparametric model. In order to determine the optimal model configuration, the GEM guidelines recommend the use of the Likelihood Ratio Test (LRT) to compare nested models (e.g. comparing ordered and partially ordered models) and the Akaike information criteria (AIC) to compare non-nested models (e.g. comparing models fit to the same data using different link functions). It is discussed in the text below that data aggregation should be avoided and that linear models fit using ordinary least squares parameter estimation (as is the case for many existing tsunami fragility functions) are unsuitable for use as fragility functions, and this is quantifiably demonstrated for the case study dataset in Sect. 4.2.

Once the statistical models have been selected they can be used to further investigate trends in the data, determine sensitivity of the derived fragility functions to explanatory variable error and missing data imputation (conducted in Step 1), and to finalise the selection of construction categories (e.g. are fragility functions to be derived for all RC buildings or derived separately for high-rise and low-rise RC buildings?). It is recommended that confidence intervals be calculated for all derived fragility functions. Whilst the proposed methodology may be used for datasets of any size, reliability will be lower for smaller datasets, and the width of the confidence intervals will give an indication of the reliability of the results. These analyses are demonstrated for the case study dataset in Sect. 4.2.

Existing studies favour parametric statistical models for the construction of tsunami empirical fragility curves. Many studies use OLS parameter estimation to fit Normal or Lognormal Cumulative Distribution Functions (CDFs) to aggregated model data, as set out in Koshimura et al. (2009). OLS models fit separate models for each of i damage states, by assigning an indicator (I ij  = 1 if damage exceeds DS i , or 0 otherwise), to each of j buildings [Eq. (1)]. The linear model assumption violations of OLS models are highlighted by Charvet et al. (2014a, b), though the effect of these violations is not quantified. OLS models are considered here to identify whether these model violations make them unsuitable for the TIM comparison of Step 3. Data aggregation must be carried out in order to form OLS models, as the inverse normal distribution function (Φ −1) is undefined at 0 and 1. Different studies aggregate data using different methods (e.g. splitting the IM range into bins of constant width, or selecting bin widths so as to ensure a constant number of observations per bin). Data aggregation by any method results in some information being lost (e.g. data distributions within IM bins are no longer accounted for), and so it is expected that model predictive power decreases and uncertainty increases. However, these effects have not been quantified in previous studies, and so it will be quantifiably demonstrated in the case study analysis (Sect. 4.2) that OLS regression is inappropriate for fragility analysis.

$$\begin{aligned} \mu_{i} = P\left( {{\text{ds}}_{j} > DS_{i} |{\text{TIM}} = x_{j} } \right) \hfill \\ \varPhi^{ - 1}( P\left( {{\text{ds}}_{j} > DS_{i} |{\text{TIM}}} \right))\sim\;{\text{normal}}\left( {\mu_{i} ,\sigma^{2} } \right), \hfill \\ {\text{where}}\;\mu_{i} = \left\{ {\begin{array}{*{20}l} {\theta_{1i} \ln \left| {x_{j} } \right| + \theta_{0i} } & {\text{cumulative lognormal}} \\ {\theta_{1i} x_{j} + \theta_{0i} } & {\text{cumulative normal}} \\ \end{array} } \right. \hfill \\ \end{aligned}$$
(1)

where \(\theta_{1i}\) and \(\theta_{0i}\) are estimated via ordinary least squares

Charvet et al. (2014a, b) postulate that GLMs should provide an improvement over OLS for deriving fragility curves, as they allow for a relaxation of some of the linear model assumptions. GLMs relate the mean of a response variable (E(y) = µ) to the explanatory variables (x i ) (with this relationship often termed the “systematic component” of the model) via an arbitrary link function (g). The link function is selected dependent on the distribution of the response variable (termed the “random component”), typically transforming the response such that g(µ) is a continuous variable bounded by [−∞, +∞]. As such, GLMs can be used for variables with distributions other than the Gaussian distribution assumed in OLS linear regression models.

A cumulative link model (CLM) may also be fit to the data whereby fragility curves corresponding to each damage state are determined by assigning a damage response indicator, ds, to each building, which is considered to follow a multinomial distribution. Each building is also assigned a TIM value, x j . The main advantage of this model over separate GLMs fit to binary data, is its ability to use all available information regarding the data in the database, and it recognises that the damage is an ordinal categorical variable and accounts for the main conclusions of the exploratory analysis (Charvet et al. 2014a). The model equation for the case of a probit link function (the inverse standard cumulative normal distribution) is given in Table 3 where β 0 and β 1 are the unknown regression parameters (the intercept and slope, respectively) estimated by a maximum likelihood optimisation algorithm. Multinomial data can be assessed using either partially ordered or ordered models. For ordered models, the slope parameters (β 1 in Table 3) are assumed to be equal for all damage states so as to avoid undesirable effects such as the crossing of fragility curves. Partially ordered models relax this assumption. Uncertainty can be quantified using bootstrap methods, as employed by Charvet et al. (2014a, b).

Table 3 Components of cumulative link models (CLM) with probit link function. It is noted that, ordered models require the slope parameter (β 1,i ) to be the same for each damage state
Full size table

Generalised additive models (GAMs, developed by Hastie and Tibshirani (1990)) are semi-parametric models that fit GLMs in a piecewise regression system with a number of separation points (or knots). Whilst there are dangers in using nonparametric and semi-parametric methods for prediction purposes (Chandler 2014), they are suitable for comparing the influence of different explanatory variables (TIMs) to describe response variable observations. However, an issue with nonparametric and semi-parametric models is that they are susceptible to over-fitting, and their appropriateness in the context of fragility analysis has not yet been demonstrated. The reader is referred to Wood (2006) for detailed instruction on the fitting of GAMs. The present study proposes and demonstrates their use for fragility analysis, as well as a sub-sensitivity method using cross-validation techniques (introduced below and demonstrated in Sect. 4.3) for avoiding over-fitting.

Step 3: Comparison and selection of TIMs

The aim of Step 3 is to use the two model types selected in Step 2 to select the TIM which best represents the dataset. This is achieved via the following procedure:

  1. 1.

    Fit the two model types selected in Step 2 to each TIM.

  2. 1.

    Calculate the K-fold cross-validation prediction error rates for both model types, for each TIM.

  3. 2.

    Pick out the TIM for which the model exhibits the lowest error rate, considering the results separately for both model types.

If the selected optimal TIM is the same for both model types, then it may be concluded that this result is not model dependent. If, however, the two model types select different TIMs, then the user may wish to consider repeating Step 3 with a third model type in order to build confidence in the results.

Cross validation is an improvement over simply plotting the residuals, as it attempts to indicate the prediction error (i.e. the proportion of incorrectly classified outcomes) that would be experienced on data that have not been used to form the statistical model. K-fold cross-validation creates K-fold partitions in the total dataset, and for each of K validation experiments uses onefold as the testing set (a different one each time), and the remaining data as the training set. The average of the error rates for all iterations gives an estimate of the true prediction error rate [shown in (2)]. Cross validation has been used to estimate tsunami fragility curve prediction error rates by Muhari et al. (2015) and Charvet et al. (2014a, b), who also propose a penalised error estimation method [shown in (3)] for multinomial models such as those used in this study. In (3), N DS refers to the number of damage states (including DS0, no damage), and the predicted damage state (ds j,predicted) for the jth observation is taken as the damage state that has the greatest probability of occurrence.

$${\text{Error}}\;{\text{rate}} = \frac{1}{K}\mathop \sum \limits_{k = 1}^{K} \frac{{n_{\text{incorrect}} }}{{N_{\text{test\,set}} }}$$
(2)
$$\begin{aligned} {\text{Error}}\;{\text{rate}}\left( {\text{multinomial}} \right) = \frac{1}{K}\mathop \sum \limits_{k = 1}^{K} \left[ {\mathop \sum \limits_{j}^{{N_{\text{test\,set}} }} \frac{{\left| {{\text{ds}}_{{j, {\text{predicted}}}} - {\text{ds}}_{{j,{\text{observed}}}} } \right|}}{{N_{\text{DS}} - 1}}} \right] \hfill \\ {\text{where}}\quad {\text{ds}}_{{j, {\text{predicted}}}} = \mathop {\text{argmax}}\limits_{{{\text{DS}}_{i} \in \left\{ {{\text{DS}}_{0} :{\text{DS}}_{6} } \right\}}} P\left( {{\text{ds}} = {\text{DS}}_{i} | {\text{TIM}} = x_{j} } \right) \hfill \\ \end{aligned}$$
(3)

Cross-validation techniques are less biased by overfitting than techniques that simply consider residuals, and so comparison of the cross-validation error rates can be used to optimise nonparametric or semi-parametric models. It is therefore recommended that K-fold cross-validation be used for sub-sensitivity analysis of GAMs in order to select models with the optimum number of knots for each TIM (demonstrated for the case study data in Sect. 4.3).

3 Presentation of case study observational and simulation data

3.1 Building damage dataset

In order to demonstrate the proposed methodology, the largest detailed dataset used to date for deriving empirical tsunami fragility curves for Japan is adopted. The building damage data used are taken from the 2011 GEJE building damage database compiled by Japan’s Ministry of Land Infrastructure Tourism and Transport (MLIT). The database is comprised of relevant information (including the number of floors, construction material and building usage) for each individual building (circa 250,000) located within the inundation area of the 2011 GEJE, though information is generally not included for every field for each building. The database represents a combination of government census data obtained before and after the 2011 Japan tsunami and damage survey data obtained by the MLIT immediately after the tsunami. All buildings are allocated a damage state from DS0 to DS6 based on the damage scale presented in Table 4 and assigned an observed inundation depth. It is noted that although each building is allocated an observed inundation depth, there is error within the observation data as they are derived from the MLIT 100-m mesh inundation database, whereby the highest observation for each 100 mx100m grid square was assigned to all buildings within that grid square. Inundation observations were primarily obtained from water marks or survivor interviews, and where no observations were present in a grid-square interpolation was conducted based on the nearest observations. The effect of this error is discussed further in Sect. 4.1.

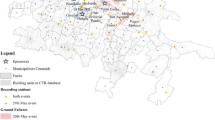
Table 4 Damage state definitions used by the Japanese Ministry of Land Infrastructure Tourism and Transport following the 2011 Great East Japan Earthquake and Tsunami
Full size table

Three case study locations are considered, namely the towns of Ishinomaki, Onagawa and Kesennuma (shown in Fig. 2), which represent 80, 15 and 5 %, respectively, of the combined dataset (67,125 buildings). Kesennuma and Onagawa experienced much deeper inundations than Ishinomaki (see Fig. 2) and also display a higher proportion of collapsed buildings (DS5*).

Fig. 2
figure 2

Case study locations with GIS images, damage state and depth distributions. GIS images have buildings coloured according to their observed damage state (right), where white buildings indicate no damage (DS0), black indicates that buildings have been washed away (DS6), and all other damage states are coloured based on a scale from green (DS1) to red (DS5)

Full size image

3.2 Tsunami inundation simulation data

To supplement the observed inundation depth data, a numerical inundation simulation is conducted for the case study locations and the quality of fit is assessed for fragility curves derived for the alternative TIMs shown in Table 5. TIM1–TIM6 have already been discussed in the context of existing studies. The drag force is proportional to the local momentum flux and so is proportional to TIM4. Tanaka and Kondo (2015) recommend changing fragility curves dependent on the Froude number, and so two additional TIMs will be considered here. Froude number will be considered directly as a TIM (TIM6), and a force estimation which depends on the flow regime will also be considered (TIM7).

Table 5 Alternative tsunami intensity measures (TIMs) considered in this investigation
Full size table

TIM7 is an equivalent quasi-steady force proposed by Qi et al. (2014) and suggested by Lloyd (2016) to represent the force of a tsunami inundation on buildings. It is evaluated via two different flow regimes determined by Froude number. The equations relate h, v and blockage ratio (building width/channel width) to the force, denoted here as F QS. Increasing the blockage ratio generally has the effect of increasing the force on the structure, and readers are referred to Qi et al. (2014) for the calculation procedure. Defining an accurate blockage ratio for each building would require knowledge of the flow direction in order to define the cross section for which “building width” and “channel width” could be measured. To conduct this calculation for each time-step of the inundation simulation would be time-consuming, and as the current study is focused on demonstrating the proposed methodology for TIM comparison, a constant blockage ratio for all buildings is assumed. For the first row of buildings, it is reasonable to assume that the flow direction is primarily perpendicular to the coast (for both the inflow and outflow), and calculating the blockage ratio accordingly for a sample of buildings gives a wide range of blockage ratios (from 10 to 90 %). Taking into account that during the inundation, several buildings were washed away, essentially increasing the channel width (i.e. decreasing the blockage ratio), for adjacent buildings, a constant blockage ratio for all buildings of 25 % will be taken in this study.

All of the simulated TIM values are calculated at the geometrical centres of each building footprint for each time-step of the simulation, and the peak values extracted, with the exception of the equivalent peak momentum flux (MFequiv, TIM5) and quasi-steady force estimation (F QS, TIM7) both of which are calculated using the separate peak depth and peak velocity values (which do not occur at the same time). This is because inundation simulations used in practice often do not provide all of the above TIMs as standard outputs, due to added computational expense, and so the effect of using the non-coincident peak depth and peak velocity to calculate more complex TIMs is investigated here, via the comparison of TIM4 and TIM5.

The numerical tsunami inundation model is presented in detail and validated by Adriano et al. (2016). The tsunami source model used in this study is the time-dependent slip propagation model presented in Satake et al. (2013). The wave propagation and inundation calculation solves discretized nonlinear shallow-water equations (Imamura et al. 1995; Suppasri et al. 2012a, b) over six computational domains in the nested grid system shown in Fig. 3. The simulation uses a simple linear vector combination to combine velocities in x and y directions. Figures 3 and 4 show inundation simulation results for Ishinomaki. The results shown are the peak values for each grid square over the simulation period.

Fig. 3
figure 3

Computational domains for the nested grid wave propagation and inundation model used for Ishinomaki (dx indicates the grid size). Results for grid size = 15 m inundation simulation are shown below in Fig. 4

Full size image
Fig. 4
figure 4

Inundation simulation results for Ishinomaki. TIM references are as defined in Table 5

Full size image

The nonlinear shallow-water equation includes the effects of flow resistance, which is parameterised using the Manning’s roughness coefficient (n). In order to achieve the most accurate results, friction may be spatially varied to account for the building density on each grid square and could be considered as a dynamically varying parameter conditional on the washing away of structures. However, as the focus of the current study is on demonstrating the proposed TIM comparison methodology, a constant and uniform Manning’s roughness coefficient of n = 0.025 is chosen to account for the flow resistance from obstacles (such as buildings and trees) in the urban case study areas, in line with current studies [e.g. Imai et al. (2013) and Charvet et al. (2015)]. Figures 3 and 4 show inundation simulation results for Ishinomaki. The results shown are the peak values for each grid square over the simulation period.

The source model was calibrated to observations from offshore buoy data by scaling the source model (the amount of fault slip or the initial tsunami height) to optimise the K-value, a spatial correlation index proposed by Aida (1978), where K is the ratio of the measured value over the computed value and so 1 indicates a good agreement (Suppasri et al. 2011). Note that this is unrelated to the K-term used to describe k-fold cross-validation discussed in Sect. 2, but as both are standard terms in their respective fields, the symbol, K, will be adopted for both here. For Ishinomaki, the original tsunami source model gave a K-value of 0.75 (i.e. the simulated flow parameters were greater than the observed), and the calibrated source model achieved a final K-value of 1.06 (i.e. the simulated flow parameters were slightly less than the observed). However, it is noted that the improved K-value does not necessarily mean good agreement between observed and simulated inundation depth at each building location. It is also noted that there are no coastal structures in the simulation except breakwaters in front of Onagawa bay.

4 Application of methodology to case study data

4.1 Step 1: exploratory analysis of data quality (case study)

4.1.1 Assessment of construction, response and inundation variables

The distinctly different damage state distributions for the case study locations shown in Fig. 2 give rise to different fragility curves if data from each town are considered separately. Despite Kesennuma and Onagawa providing large individual datasets, most of the buildings in these towns sustained damage levels DS5 or DS6, which would result in fragility curves for lower damage states being associated with low confidence. A closer look at the data shows that the distributions of buildings with different construction materials are similar for the three towns and that together they provide a better coverage of a range of inundation depths. Hence, it is reasonable to combine the data from the three towns in order to provide a larger dataset, so enabling greater confidence in the derived fragility curves.

Producing fragility curves for each construction material requires splitting the data into small datasets for some materials (e.g. Kesennuma has only 112 steel buildings, spread over the 5 damage states), which can result in larger errors associated with the model parameter estimates. It can be observed that damage state distributions for wood and masonry, (typically considered non-engineered construction materials), are very similar to each other, and the same can be observed of the damage distributions associated with reinforced concrete (RC) and steel construction materials, typically considered as engineered construction materials. Comparison between the damage distributions of buildings of engineered and non-engineered construction materials instead shows significant differences. Hence, in this paper, fragility curves are developed for buildings of engineered and non-engineered construction materials (termed “engineered” and non-engineered buildings” for the remainder of this paper) in order to account for the significant differences in the fragilities of such buildings, whilst maintaining large enough datasets to avoid greatly increasing uncertainty in the model parameter estimates.

Upon inspection of the response variable (damage state) definitions, it can be seen that DS5 and DS6 do not represent progressively worse damage states. These should therefore be combined for fragility function derivation [as per Charvet et al. (2014a, b)], and so for the remainder of this study damage states 5 and 6 are combined and collectively termed as DS5* as shown in Table 4.

Figure 5 compares observed and simulated inundation depths for all 67,125 buildings. On average, the simulation overestimates the observed depth by 0.1 m (Fig. 5b), but tends to overestimate values at lower depths, and underestimate higher depths (Fig. 5c). These discrepancies are expected because local increases in flow depth at obstacle locations are not considered in the model, but the observed field measurements will include traces that will exhibit this increased depth. Furthermore, spatial and temporal variation of the flow resistance due to the destruction of obstacles is not modelled. It is also important to note that there may be error in the observed depth values for the reasons outlined in Sect. 3.1. It is not possible to estimate the error in the observation data with the available information, but by investigating variation in simulated data, it can be seen that buildings within the same square of a 100-m grid can have simulated depths which differ by a mean of 0.8 m, a third quartile of 1.08 m and a maximum of 5.2 m. Therefore, the discrepancies shown in Fig. 5 should not be considered as due to simulation error only, but due to errors in both observations and simulations.

Fig. 5
figure 5

Comparison between observed and simulated inundation depths. a, d The distribution of observed and simulated depth, respectively, with corresponding Gaussian curves. c The correlation (correlation coefficient 0.91), with the outer red diagonals indicating the 2 m error band. b The distribution of the error (simulated–observed), with corresponding Gaussian curves

Full size image

Whilst it is possible to validate simulated inundation depth results, there is insufficient velocity observation data to make a meaningful comparison beyond that presented in Adriano et al. (2016). Park et al. (2013) compare simulated depth, velocity and momentum flux values to experimental results, and Park et al. (2014) conduct a sensitivity analysis of the same TIMs to friction coefficient and modelling software. Both studies find that where changes in simulation parameters may lead to small changes in depth, changes in velocity and momentum flux can be much greater (a 15 % change in depth was reported to correspond to a change in velocity and momentum flux of 95 and 208 %, respectively). This is likely due to the fact that the mass of water on land will be reasonably well predicted (because the flux is essentially calibrated from the flow data). However, the flow speed depends on the fidelity of the flow dynamics in the model. Therefore, the discrepancies in Fig. 5 suggest the possibility of much greater potential error in TIMs related to velocity and momentum flux, though this cannot be verified with the available data. The implications of these potential discrepancies are discussed in Sect. 4.3.

4.1.2 Treatment of incomplete data entries

Figure 6 shows the distribution of construction materials aggregated across all case study locations. Buildings of unknown construction material (denoted “unknown”) make up 18.1 % of the total dataset within the inundated area, representing a significant proportion of the data and so it is necessary to analyse this missing data further so as to avoid the introduction of bias.

Fig. 6
figure 6

Construction materials aggregated across all case study locations (67,125 datapoints) for (from left to right) RC

Full size image

If the missing data were MCAR (see Table 1), then there should be no relationship between the buildings that have missing material data and other attributes such as the building height, size and use. However, analysis of building footprint sizes (Fig. 7) suggests that engineered buildings (RC and steel) are generally larger than non-engineered buildings (wood and masonry), with buildings of unknown material representing the smallest footprints. This suggests that many buildings of unknown material may represent non-engineered buildings. A Kolmogorov–Smirnov test is conducted and confirms that footprint areas for the buildings of unknown material are not of the same distribution as for the total dataset (i.e. they have different probability density functions). Therefore, the missing building material data are not MCAR. MNAR would refer to, for example, if wooden buildings are more likely to have missing material data because they are wooden. However, there is no reason to believe that all the missing material data can be associated with either the engineered or non-engineered construction types. Hence, the missing building material data are not considered MNAR. MAR would be the case where, for example, small buildings are more likely to have missing material data, but this has nothing to do with material after accounting for size. This is more likely to be the case here, and hence we adopt a MI approach to assign building data for which construction material information is missing to either the engineered or non-engineered building categories.

Fig. 7
figure 7

Damage state distributions, showing that buildings of unknown material type have a greater proportion of undamaged (DS0) buildings than buildings of known material type. Histograms and normal curves for building inundation depths and footprint areas for all buildings (left), buildings of unknown material only (centre), and buildings of known material (right)

Full size image

Which attributes should be used for the imputation? It has been already shown that building footprint is an indicator of construction material. Figure 7 also shows that buildings of unknown material show a large proportion of undamaged (DS0) buildings. Given that the dataset is a combination of census data and damage survey data, it might be speculated that building material was only recorded during the damage survey, which did not investigate undamaged buildings in detail. Visualisation of building location by construction material shows no obvious spatial correlation of the unknown buildings. However, a Kolmogorov–Smirnov test performed on the observed inundation depths for unknown and known materials indicates that there is a very low probability (<5 %) that the two datasets are drawn from the same underlying distribution. Figure 7 shows that the distributions of inundation depths for buildings of unknown material do have a slight increase in the number of buildings at low simulated inundation depths. As undamaged buildings are more likely to fall within the unknown material category, and buildings are more likely to remain undamaged at the outskirts of the inundation area, then it is to be expected that there are slightly more unknown buildings experiencing low inundation depths. In addition, building use shows some correlation with construction material. Therefore, MI analysis, with 4 imputations, is conducted in order to estimate building material based on footprint area, damage state, building use and observed inundation depth. The effect of imputation on results is presented in Sect. 4.2.1.

4.2 Step 2: Statistical model selection and trend analysis (case study)

4.2.1 Model selection and configuration optimisation

In this stage, several statistical model types and model configurations are investigated and the models used for the TIM comparison of Step 3 are selected. It is noted that the TIM used in this section is the observed inundation depth reported in the MLIT database, and therefore this investigation is independent of the inundation simulation.

It is decided that of the model types proposed in Table 2, two will be selected from OLS, CLM and GAMs. Two stages of analysis are conducted in order to identify the most appropriate statistical model types and configurations for representing the imputed dataset: first a comparison of ordered and partially ordered CLMs, then a comparison of CLMs and OLS models for different aggregation methods. The model configurations considered are summarised in Table 6. As indicated in Table 2, analysis can be conducted to select the optimal link function and determine whether a transformation should be performed on the TIMs. The reader is referred to Charvet et al. (2014b) for examples of this analysis, and for brevity in the present study, probit link functions have been chosen, and all analyses are conducted on the logarithm of each TIM.

Table 6 Summary of models used in sensitivity analysis of statistical methods
Full size table

“Goodness of fit” tests such as R 2 and AIC cannot be used to directly compare cumulative models (multinomial random component) with separate models (binomial random component), nor to compare models formed on aggregated and disaggregated data. In these cases, cross-validation methods may be employed. Tenfold cross-validation is therefore conducted for each model, whereby the penalised prediction error rate [Eq. (3)] is repeatedly estimated until the difference between the running average and that of the previous iteration reduces to below 10−5.

First, it is determined whether partially ordered or ordered models (models M1.1 and M1.2, respectively) should be used. A more complex model (partially ordered model, M1.1) will always fit the data as well as or better than a simpler model (M1.2), as shown by the error rates given in Table 6. The Likelihood Ratio Test (LRT) confirms whether this improvement in fit is significant, and the results given in Table 7 confirm that there is less than a 1 % chance that the improvement in fit for the more complex model could be observed by random chance. Therefore, the partially ordered model (M1.1) is to be used for the TIM comparison in Step 3.

Table 7 Likelihood Ratio test results for ordered and partially ordered models, showing that the partially ordered model provides a significantly better fit than the ordered
Full size table

Second, it is confirmed that data aggregation and OLS parameter estimation are unsuitable for TIM comparison and should not be permitted for fragility function derivation. The effect of data aggregation is examined by fitting a partially ordered CLM (Table 3) to the data aggregated into 10 TIM bins of equal width (model M2.1). Table 6 shows that the predictive error rate is higher than that of the corresponding model fit to disaggregated data (model M1.1), confirming that data aggregation can reduce model accuracy. The effect of parameter estimation is then examined by fitting an OLS model [Eq. (1)] to the same aggregated data (model M2.2). Table 6 shows that the predictive error rate is higher than that of the corresponding aggregated CLM model (M2.1), showing that the OLS linear model violations do reduce the accuracy of the model. Sensitivity to aggregation method is then examined by fitting CLM and OLS models (M2.3 and M2.4, respectively) to data aggregated into 10 IM bins, where bin width is determined so that each bin contains the same number of buildings. Table 6 shows that the predictive error rates are different from the corresponding models fit to data aggregated by alternative methods (M2.1 and M2.2, respectively) showing that results are sensitive to the aggregation approach. It is also noted that aggregated data prevent the use of imputation methods and much of the exploratory analysis presented in this study, meaning that it is more difficult to identify and remove bias and complete missing data. Given that data aggregation reduces model predictive accuracy by an amount which is dependent on aggregation approach suggests that disaggregated data is always preferred. This issue is compounded for OLS models where the linear model assumption violations have been shown to result in a further reduction in model accuracy and increased sensitivity to aggregation method. Note that this is a significant and general result, and therefore, existing studies which use aggregated data from the 2011 GEJE should be considered superseded by those which use disaggregated data.

As GAMs are a piecewise system of GLMs, and as overfitting can be avoided using cross-validation sub-sensitivity analysis (demonstrated in Sect. 4.3) GAMs are also selected (alongside CLM model M1.1) to conduct the TIM comparison of Step 3.

4.2.2 Trend analysis and sensitivity analyses

Trend analysis is conducted using the selected CLM (M1.1) in order to further investigate the influence of construction material and the data imputation presented in Sect. 3.2.

Model M1.1 is fit to all 67,125 data, where fragility curves corresponding to the five damage states (DS1–DS5*) are determined. Curves are constructed for engineered and non-engineered building categories, and the influence of these construction material groups is examined by fitting the CLM expressed by the equations in Table 3 to the data corresponding to the two material groups. Confidence intervals are calculated using bootstrap methods based on 1,000 iterations, as per Charvet et al. (2014a, b). Figure 8 shows that fragility curves for engineered and non-engineered buildings differ in both slopes and intercepts, and so it is appropriate to consider these material groups separately. Consequently, the TIM comparison of Step 3 is conducted for each material group separately, and results are compared.

Fig. 8
figure 8

Comparison of fragility curves for engineered and non-engineered material groups, for each damage state, formed on disaggregated data

Full size image

The next question that should be addressed is whether the MI process outlined in Sect. 3.1 yields significantly different fragility curves, compared to those derived from the data where the missing data are ignored. Figure 9 shows a sensitivity analysis whereby fragility curves are compared for engineered buildings formed on the imputed data and the original data (with missing data removed). The difference in the mean curves with and without using MI confirms that the removal of data with missing information on construction material leads to a bias for the case of this dataset. Furthermore, the limited variation in the mean curve for each of the imputations shows that although 18.2 % of the data is missing, materials estimated using MI provide relatively stable results. All analyses conducted throughout the remainder of this study are conducted on the completed (imputed) data (Fig. 9a).

Fig. 9
figure 9

Imputed data: a sensitivity analysis of derived fragility curves for engineered structures to the MI method applied to estimate unknown building materials. Dashed-lines show curves formed using complete-case analysis (ignoring missing data). Solid lines show the mean curve for the imputed dataset which is used throughout the remainder of this study, and the indicated range for each curve shows the maximum/minimum values for the mean curves derived separately on each of the four imputations

Full size image

Finally, given the discrepancy between observed and simulated inundation depth highlighted in Sect. 3.2, it is necessary to examine what effect this may have on the produced fragility functions. Figure 10 confirms that fragility curves for observed and simulated depths are different, and it is also noted that the model fit to simulated inundation depth gives a higher error rate than that fit to observed depth. Figure 11a, b presents fragility curves where outliers have been removed, where outliers are assessed as corresponding to discrepancies between observed and simulated inundation depths of 1 and 2 m, respectively. These figures show that the mean curves are not sensitive to removal of outliers corresponding to at least 2 m discrepancy (8.9 % of buildings), but narrowing the allowable discrepancy to 1 m (32.3 %) has a large effect on the mean curves. The selection of a threshold beyond which to remove outliers is subjective, and discrepancies between observed and simulated results do not prevent the assessment of the relative accuracy of various simulated TIMs in describing observed damage, as the same outliers are present for all TIMs. Therefore, the remainder of this study uses the complete dataset (with no outliers removed), but it should be noted that following the arguments set out in Sect. 3.2 the expected error for simulated TIMs relating to velocity and force are expected to be greater than those associated with depth only.

Fig. 10
figure 10

Comparison of fragility curves for simulated (dashed line, error rate = 15.9 %) and observed (solid line, error rate = 11.3 %) inundation depth, for engineered buildings (partially ordered probit model)

Full size image
Fig. 11
figure 11

Sensitivity to outliers. Probit models for observed inundation depth and engineered (RC and Steel) construction materials using the imputed disaggregated dataset, with datapoints of more than a a 1-m discrepancy and b 2-m discrepancy removed (corresponding to a loss of 32.3 and 8.9 % of datapoints, respectively)

Full size image

4.3 Step 3: Comparison and selection of TIMs (case study)

This section compares several Tsunami Intensity Measures (TIMs) in their ability to describe the observed damage data. Partially ordered probit models (model M1.1) are fit to the disaggregated data of the MLIT building damage database for each of the TIMs identified in Table 5, and their relative fits are compared using prediction error rates estimated via tenfold cross validation. The same procedure is then conducted using GAMs. Finally, the TIMs are ranked by their predictive error rates for both the CLM and GAM model groups.

As GAMs fit GLMs in a piecewise regression system with a number of separation points (knots), it is necessary to select the number of knots so as to optimise the fit to the data but avoid overfitting. Cross-validation techniques are less biased by overfitting than techniques that simply consider residuals, and so K-fold cross-validation is used for sub-sensitivity to select the optimum number of knots. Table 8 shows that for a series of GAMs fit to observed inundation depth, the model using 4 knots provides the lowest error rate and so provides the optimal fit over GAMs with more knots, which exhibit signs of overfitting (Fig. 12). This sub-sensitivity analysis is repeated so as to identify the optimal number of knots for each TIM in turn.

Table 8 Tenfold cross-validation error rates for GAMs over a range of knots
Full size table
Fig. 12
figure 12

Comparison of fragility curves for GAMs (probit link function) with 4 (M1.3) and 7 (M1.4) knots, showing optimal and over-fit curves, respectively. Note that aggregated datapoints are shown for graphical reference, but have not been directly used in the regression analysis, which has been conducted on the imputed disaggregated dataset

Full size image

Tables 9 and 10 compare the prediction error rates for CLMs and GAMs fit to each simulated TIM, for engineered and non-engineered buildings, respectively. Figure 13 shows fragility functions fitted to the best and worst performing TIMs for engineered buildings (F QS and Fr, respectively) showing narrower confidence intervals for the better performing TIM.

Table 9 Engineered Buildings: comparison of prediction error rates for partially ordered cumulative link models
Full size table
Table 10 Non-engineered Buildings: comparison of prediction error rates for partially ordered cumulative link models
Full size table
Fig. 13
figure 13

Derived fragility functions (partially ordered CLMs with probit link functions fitted to ln|TIM|) for engineered buildings for the best (left) and worst (right) performing TIMs (F QS and Fr, respectively)

Full size image

For engineered buildings, the quasi-steady force estimation (F QS) and simulated inundation depth (h sim) appear to give the best fit. The fact that the results for CLMs and GAMs are similar suggests that the results are not model-specific. For non-engineered buildings, the GAMs fit to each TIM follow a similar pattern to that for the engineered buildings, i.e. that F QS and h sim appear to give the best fit. However, the CLMs fit to non-engineered data do not fit this pattern (Table 10), showing both momentum flux estimations (MF and MFequiv) as the optimal TIMs, though with error rates very close to F QS. This discrepancy suggests that the results are model-specific for the non-engineered category. This difference in results between CLMs and GAMs for non-engineered buildings may be due to the greater uncertainty in performance for non-engineered buildings compared to engineered buildings (i.e. there is likely to be less variation in performance amongst RC and steel buildings, all of which will have been designed and constructed to similar standards). Furthermore, non-engineered buildings are likely to be more susceptible to additional damage mechanisms that may not be well represented by the TIM, such as debris impact and preceding seismic damage [effects which could only be ruled out for analytical damage data based on structural analysis (Macabuag and Rossetto 2014)]. That GAMs and CLMs treat this uncertainty differently may account for the reason that they pick out different optimal TIMs for non- engineered buildings (which have high uncertainty), and also why they pick out the same TIM for engineered buildings (which have lower uncertainty). In order to build confidence in the results for non-engineered buildings, it would be possible to break down the non-engineered category back into its constituent construction materials (masonry and wood), and to repeat Step 3 using a third statistical model, as per the feedback loop in Fig. 1.

Velocity and Froude number alone are consistently the worst TIMs. However, F QS (a function of h, v and Fr) generally performs better than the traditional force measure of momentum flux (a function of h and v only). The implications of these findings for the construction of future empirical and analytical fragility functions are that force should be used as a TIM, where either force accounts for the flow regime (for 2D curves) or an indicator of the flow regime (e.g. Froude number) should be investigated as an additional TIM (for fragility surfaces). In addition, blockage ratio may be calculated for each building (as discussed in Sect. 3.2) to further improve this result.

The equivalent peak momentum flux is seen to provide a better fit to the data than the instantaneous peak momentum flux (MF). This suggests that the non-coincident depth and velocity can be combined without significant loss of damage predictive power. That is not to say that momentum flux calculated from non-coincident peak depth and velocity is an accurate estimate of instantaneous peak momentum flux [this has been shown to not be the case by Park et al. (2013)], but that equivalent momentum flux is as good a descriptor of building damage as peak momentum flux. However, velocity outputs of the inundation model should be further validated in order to verify this result. It is noted that F QS (consistently amongst the best performing TIMs) is an equivalent value calculated from the non-coincident peak depth, velocity and Froude number.

It is highlighted that this outcome has been reached despite the likely greater observation errors in simulated velocity and momentum flux than depth discussed in Sect. 3.2. This indicates that depth may be a preferred TIM where inundation simulation accuracy is thought to be low, and measures of force are the preferred TIMs where simulation accuracy is thought to be high, or where velocity can be validated [e.g. through experiments such as carried out by Park et al. (2013)]. However, to verify this conclusion, it would be necessary to use models that take into account measurement error, and optimally to use sets of data with low and high measurement error.

5 Summary and conclusion

This paper has collated, compared and expanded on the current state-of-the-art methodologies for tsunami fragility assessment, in order to present a three-stage methodology for the selection of the optimal Tsunami Intensity Measure (TIM) for empirical fragility function derivation for a given dataset. This methodology is demonstrated using a detailed, disaggregated damage dataset from the 2011 Great East Japan earthquake and tsunami, unique in the fields of both tsunami and seismic fragility assessment.

First, exploratory analysis is conducted, showing that buildings of unknown construction material present a significant proportion of the total dataset (18.2 %). In order to avoid the introduction of bias when producing fragility curves by material, missing material data are estimated using MI techniques. Second, a sensitivity analysis of several statistical methods is conducted, so as to select at least two statistical models with which to conduct the TIM comparison. General conclusions are drawn regarding the suitability of various models and the methods used to select between them, with a CLM and GAMs selected for the TIM comparison. Further exploratory analysis is then conducted using these statistical models. Third, numerical inundation simulation results are used to consider several alternative TIMs. Comparison of observed and simulated inundation depths shows some disagreement, suggesting that there may be further (and perhaps more significant) error in simulated velocity and other parameters. Partially ordered probit models are derived for several TIMs, and their tenfold cross-validation results are compared. The same procedure is repeated using GAMs to show that the results are not model-specific. It is shown that the quasi-steady force estimation (F QS) and inundation depth consistently provided the best fit to the observed damage for engineered buildings.

The main conclusions of this study can be summarised as follows:

Exploratory analysis

  1. 1.

    Missing data can only be removed if it can be shown to be missing completely at random. This is shown to be not the case for the 2011 MLIT Japan data, meaning that all previous studies which have generated curves according to any sub-category (e.g. material, age, height) using complete-case analysis (removal of buildings with missing data) may have introduced a bias in the results.

  2. 3.

    Multiple imputation (MI) has been shown to be an acceptable method for estimating missing data and is recommended for use on future fragility studies where data cannot be shown to be missing completely at random.

Statistical modelling

  1. 4.

    K-fold cross-validation (KFCV) is shown to be a suitable method for comparing model fits for various model types, and the methodology for conducting this for multinomial models is demonstrated. It is recommended that KFCV be used for evaluation of model fits in future fragility studies.

  2. 5.

    Data aggregation has been quantifiably shown to reduce model predictive accuracy by an amount which is dependent on the aggregation approach. Hence, existing studies that use aggregated data from the 2011 GEJE should be considered superseded by those that use disaggregated data directly.

  3. 6.

    Ordinary least squares parameter estimation is quantitatively shown to be unsuitable for fragility function estimation as it suffers from the issues of data aggregation and violates several linear model assumptions leading to reduced predictive accuracy and increased uncertainty.

  4. 7.

    Semi-parametric methods are seen to be suitable for comparative fragility assessments, and the issue of over-fitting can be avoided through the use of cross-validation techniques, as demonstrated.

Optimal tsunami intensity measure

  1. 8.

    Measures of force appear to provide the most efficient TIMs, if the inundation simulation from which they are derived is sufficiently accurate, or simulated velocity can be validated. Depth is an acceptable TIM for low-accuracy simulations of inundation. The required accuracy is the subject of further research.

  2. 9.

    Inundation simulation outputs recommended for fragility assessment are depth, velocity and Froude number, as instantaneous force values (calculated at each time-step) do not appear to give better fits to observed damage than equivalent values calculated from separate (non-coincident) peaks of depth, velocity and Froude number. Further research is needed to investigate the sensitivity of this result to inundation simulation accuracy.

  3. 10.

    Flow regime (indicated by Froude number) appears to be a significant consideration when conducting fragility assessments or quantifying tsunami-induced forces on structures.

Based on the conclusions above, this paper recommends that existing fragility assessments should be re-examined for potential bias if they have been based on complete-case analysis of data subsets (e.g. construction material), aggregated data (where disaggregated data are available), or OLS parameter estimation. With the introduction of several concepts novel to the field of fragility assessment (MI, GAMs, KFCV for model optimisation/comparison) and the finding that force measures considering flow regime provide the most efficient TIM for high accuracy inundation simulations, this study has significant implications for the future generation of empirical and analytical fragility functions.