Abstract
The evaluation of the intensity of unrest phases at active volcanoes is a crucial topic in volcano hazard studies. This is particularly troublesome in the case of persistently active volcanoes like Stromboli (Southern Italy), where intense eruptive summit activity (overflows, strong spattering, powerful explosions) has in some cases anticipated a flank eruption. In this context, a new approach for the analysis of displacement data is introduced. Daily displacements of the Stromboli crater terrace measured between January 1, 2010, and August 7, 2014, by a ground-based interferometric synthetic aperture radar system were compared, in retrospect, to displacement predictions provided by an auto-regressive integrated moving average-based model. The methodology consisted in assessing when the actual displacements exceeded a fixed probability threshold for the forecasts (~95 %). Two sets of data were consequently produced: (1) series of residuals between actual displacements and model threshold (“anomalies”) and (2) series of normalized residuals between actual displacements and model threshold (“normalized anomalies”). This permitted to statistically identify and quantify the anomalous deformation at the crater terrace over the reference time interval of the analysis. Anomalies started to occur before each period of intense volcanic activity, highlighting the possibility to discern between background activity and unrest. Moreover, results indicated that the inflation of the crater terrace during the preparatory phase of the 2014 flank eruption was characterized by the greatest amount of anomalous deformation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Volcanic unrests, defined as “changes from the normal state” at volcanoes (Newhall and Dzurisin 1988), are common phenomena frequently recorded by monitoring networks. The shift from background activity to unrest depends on the approach used to define the threshold between these two states of a volcano (Potter et al. 2015). A generic and exportable statistical method is used herein to identify different levels of volcanic activity from volcano displacement data recorded by a ground-based interferometric synthetic aperture radar (GBInSAR) system (Rudolf et al. 1999; Luzi et al. 2004; Barla et al. 2010; Intrieri et al. 2015) at Stromboli volcano (Southern Italy). Stromboli is a persistently erupting volcano that experiences frequent unrest phases, sometimes followed by flank eruptions, strong explosive activity and tsunamis (Barberi et al. 1993; Rosi et al. 2013). GBInSAR is an efficient technique for capturing inflation in open vent volcanoes like Stromboli, because it can detect very shallow magma storage, which is difficult to identify using other methods (Casagli et al. 2007; Di Traglia et al. 2013, 2014a, b, c, 2015). A ground-based radar permits the user to choose the optimal instrument location for measurements (Wadge et al. 2008, 2014), providing also an exceptional geometrical resolution and allowing for continuous monitoring of the displacements with a very high sampling rate (up to 1 min; Di Traglia et al. 2014a), if compared to space-borne InSAR data (up to 4 days; Pinel et al. 2014). Daily displacements acquired by the GBInSAR between January 1, 2010, and August 7, 2014, were analyzed in order to define the periods of anomalous deformation of the summit crater terrace. The study focused on determining whether the inflation of the summit crater terrace prior to the August 2014 flank eruption could be numerically distinguished from the inflation occurred during periods of volcanic activity which did not lead to flank effusions. In particular, the method involved employing a well-established statistical approach largely used in the field of econometrics for time series analysis, derived from the work of Box and Jenkins (1976) and Box et al. (1994) on the auto-regressive integrated moving average (ARIMA) models.
2 Geological and volcanological background
Stromboli volcano is located in the Tyrrhenian Sea off the Southern coast of Italy (Fig. 1). Stromboli gives the name to Strombolian activity (Mercalli 1881), which is characterized by intermittent explosions at a typical rate of 1–10 events per hour (Blackburn et al. 1976; Patrick et al. 2007; Harris and Ripepe 2007). The ordinary Strombolian activity is occasionally interrupted by higher-intensity explosions, usually referred to as “major” or “paroxysmal” events (Barberi et al. 1993; Rosi et al. 2013). Effusive eruptions can occur at Stromboli volcano as overflows (103 m3–105 m3 volume), generally short-lived (up to 1 day; Rosi et al. 2013) and comprising both intra-crater lavas flowing within the crater terrace and lava tongues that descend the NW flank of the volcano, and large lava flows (106–107 m3 volume) fed by fissures or ephemeral vents that can remain active for months (Barberi et al. 1993; Rosi et al. 2013). These lavas use to form lava flow fields which eventually can reach the coast, where they can form lava deltas. The volcano was affected by three sector collapses, one of which occurred 13 ka in the NW part of the edifice and produced a scar called “Sciara del Fuoco” (Tibaldi 2001). Another large collapse event took place 5.6 ± 3.3 ka (Tibaldi 2001), producing a massive landslide (0.73 ± 0.22 km3, Di Roberto et al. 2008); this event has been related to a large explosive eruption (Bertagnini and Landi 1996; Petrone et al. 2009). The most recent landslide of notable importance (25–30 × 106 m3) happened during the 2002–03 flank eruption (Bonaccorso et al. 2003; Baldi et al. 2008), which was triggered by the injection of a lateral intrusion (Neri et al. 2008) and caused two tsunami sequences with a maximum run-up of 6–7 m at Stromboli village (Tinti et al. 2006a, b). In this instance, the GBInSAR system detected low displacement rates (0.001–0.01 mm/h) along the Sciara del Fuoco, suggesting creep behavior of the volcaniclastic material filling the depression (Nolesini et al. 2013). Planar deep creep occurs in fact on long slopes when the strata dip parallel to the slope (Intrieri et al. 2013a; Di Traglia et al. 2014b).
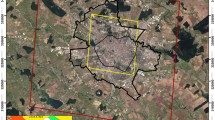
Localization of Stromboli volcano (upper left) and recent history of its deformation.* a Cumulative displacement map recorded by the GBInSAR system of the crater terrace and of the northwestern flank of the Sciara del Fuoco at Stromboli volcano, showing the total line-of-sight (LOS) displacement as measured in recent years (January 1, 2010–August 7, 2014). The red circle indicates the reference point used for the time series displayed in b–d. b–c Daily and cumulative displacements of the radar-monitored area shown in a. d Cumulative displacements of the same monitored area during the three time segments indicated in b, c. Each of these periods has been characterized by intense volcanic activity, raising the level of concern of the civil protection. However, only the last one evolved into a flank eruption.
* The cumulated displacement map and time series are produced by the LiSA (Linear SAR) system developed by Ellegi LLC using proprietary GBInSAR technology by LiSALab LLC, a European Commission Joint Research Centre spin-off, and installed at Stromboli by the Dipartimento di Scienze della Terra—Università di Firenze (owner of the system), in the framework of the research agreements (SAR.net, SAR.net2, InGrID and InGrID2015 projects) with the “Presidenza del Consiglio dei Ministri—Dipartimento della Protezione Civile” (Presidency of the Council of Ministers—Department of Civil Protection). The background topographic data are represented by a very high resolution digital elevation model (DEM) having a spatial resolution of 50 cm provided by the “Presidenza del Consiglio dei Ministri—Dipartimento della Protezione Civile” (Presidency of the Council of Ministers—Department of Civil Protection) to the Dipartimento di Scienze della Terra—Università di Firenze in the framework of the research agreements SAR.net, SAR.net2, InGrID and InGrID2015 projects. This DEM was obtained elaborating the 3D data (8 pt/m2) acquired during the airborne laser scanning survey carried out from May 04, 2012, to May 18, 2012, by BLOM Compagnia Generale Riprese aeree S.P.A. (www.blomasa.com). The data were acquired using the Leica ADS80 sensor, whose instrumental vertical and horizontal accuracy is ±10/20 and ±25 cm, respectively. Map was generated using ESRI platform
Unrests at Stromboli are characterized by changes in the background activity of the volcano in terms of frequency and intensity of the Strombolian explosions. On average, during the background activity, the explosions occur at a rate of <10 events/hour, shifting to a rate of >14 events/hour during unrests (measured by thermal cameras, Calvari et al. 2014). This shift is commonly associated with changes in the features of the erupted products (Lautze and Houghton 2005, 2007; D’Oriano et al. 2011) and in the parameters monitored by the geophysical (Casagli et al. 2007; Ripepe et al. 2009; Calvari et al. 2014; Coppola et al. 2012; Di Traglia et al. 2014b) and geochemical monitoring network (Aiuppa et al. 2009, 2011; Inguaggiato et al. 2011). Modeling ground displacements collected at Stromboli by the GBInSAR from January 2010 to August 2014 revealed a deformation source at 482 ± 46 m a.s.l. (Di Traglia et al. 2015). During this period, the volcano experienced several episodes of intense volcanic activity, culminated in the effusive flank eruption of the August 7, 2014. The modeled deformation allowed Di Traglia et al. (2015) to estimate a cumulative volume change of 4.7 ± 2.6 × 105 m3 and a stored strain energy of the source available on 6–7 August of 3.3 ± 1.8 × 1014 J, 3–5 times greater than the surface energy needed to open the eruptive fissure.
Ground deformation analysis by Di Traglia et al. (2014c) revealed that changes in the displacement time series extracted in this area are coupled with variations in seismic tremor amplitude and are anticipated by few days by the changes in the amplitude of the very-long-period (VLP) signals. This temporal delay between the changes in tremor amplitude of the VLP signals and the GBInSAR displacements is interpreted in terms of the different timescales characterizing bulk gas transfer versus slug formation and ascent (Di Traglia et al. 2014c). Moreover, discrete Fourier transform analysis of the same displacement time series shows that the most energetic peaks correspond to a period of 256 days, comparable to the residence time in the very shallow magma storage system (10–213 days; Gauthier and Condomines 1999; Gauthier et al. 2000). This suggested that the deformation of the crater terrace area is controlled by the accumulation of magma in the shallow storage system (Di Traglia et al. 2015).
3 Materials and methods
3.1 The GBInSAR system
GBInSAR is a system able to measure line-of-sight (LOS) ground displacement in the time interval between two acquisitions. The displacement is calculated from the phase difference between the back-scattered microwave signals received at different times through the cross-correlation of two SAR images. Images are obtained through sampling techniques, so frequency and spatial steps have to be selected in order to avoid ambiguity in range and cross-range (Antonello et al. 2004). At Stromboli, the GBInSAR produces one SAR image of the NE flank of the crater area and of the upper part of the Sciara del Fuoco every 11 min. Range and cross-range resolutions are on average 2 m x 2 m, with a measurement precision referred to the displacement of less than 1 mm (Casagli et al. 2007). A coherence threshold (0.8) is set to mask the noisy areas of the interferogram (Luzi et al. 2010). The phase values can be affected by ambiguity (unwrapped phase) but, due to the short elapsed time (11 min) between two subsequent measurements on Stromboli volcano, the interferometric displacements are usually smaller than half wavelength, and therefore, unwrapping procedures are not necessary. Displacements can be estimated with high accuracy by stacking the phase of the interferograms, i.e., by processing many images together rather than adopting a more classic two-image approach. At Stromboli, the GBInSAR combines all the 8-hour-averaged images (Zebker et al. 1997; Antonello et al. 2004; Intrieri et al. 2013a), producing cumulative displacement maps and displacement time series with an accuracy of ±0.5 mm (Di Traglia et al. 2014c, 2015). Interferometric stacks are useful to highlight persistent deformation, suppressing other random signals, like atmospheric anomalies (Pinel et al. 2014). This approach is appropriate when the deformation is episodic with no change in source parameters over time, as observed by Di Traglia et al. (2015) at Stromboli. The GBInSAR time series extracted in this study derives from an area located on the external part of the crater terrace (red circle in Fig. 1), characterized by a high coherence of the signal and by measurements that have displayed over time the best consistency and accuracy. The time series in Fig. 1 are those used by Di Traglia et al. (2014c, 2015). Time series data were synthesized to daily displacement values spanning from January 1, 2010, to August 7, 2014. Data from Di Traglia et al. (2013, 2014a, b, c, 2015) revealed that remarkable inflation of the crater terrace area occurred in three different periods (Fig. 1):
-
July–December 2011 (blue box and line);
-
September 2012–May 2013 (red box and line);
-
May–August 2014 (green box and line).
The range of variation of the daily displacements appears to be similar across the three phases of inflation. Peak values were registered on August 22, 2011, March 28, 2013, and August 2, 2014. The greatest amount of cumulative deformation was measured between September 2012 and May 2013.
Similarly, three periods of volcanic unrest were defined by several authors based on the observation of intense volcanic activity (Coppola et al. 2012; Calvari et al. 2014; Di Traglia et al. 2014a, b, c, 2015; Rizzo et al. 2015; Calvari et al. 2016):
-
the 2011 unrest (June 2011–September 2011), characterized by the occurrence of 7 major explosions and 2 effusions from the crater terrace (major eruptive events in July and August 2011).
-
the 2012–2013 unrest (December 2012–May 2013), characterized by several small effusions from the crater terrace, with phases of intense effusive activity. However, no major explosion was detected (major effusive events in December 2012–January 2013 and April 2013).
-
the 2014 flank eruption (June 2014–November 2014), characterized by several small effusions from the crater terrace between June and August 2014; the peak of activity was reached on August 7, 2014 with the opening of a fissure and the onset of an effusive eruption on the NE flank of the summit cone.
These unrest periods led the civil protection authorities to require a level of attention to the scientific institutions involved in the monitoring network at Stromboli (Istituto Nazionale di Geofisica e Vulcanologia and the Department of Earth Sciences—University of Firenze). In the following sections, both the 2011 and 2012–2013 unrest phases will be indicated as “minor” unrests, as opposed to the 2014 “major” unrest which evolved to a flank eruption.
3.2 ARIMA models
ARIMA models are well-established statistical methods for time series fitting and forecasting originally born in econometrics (Box and Jenkins 1976; Box et al. 1994; Bourbounnais 2005). They soon became widely applied in a variety of other scientific fields as well, such as civil engineering, environmental engineering and meteorology (e.g., Van der Voort et al. 1996; Rajesh and Krithika 2009; Faruk 2010). They incorporate both an autoregressive and a moving average approaches, as follows:
where \(\varphi_{1} , \ldots ,\varphi_{p}\) are the parameters of the autoregressive model, C is a constant, ε t a white noise variable, and ϑ 1,…, ϑ q are the parameters of the moving average model. The notation ARIMA (p,q) therefore refers to a model with p autoregressive (AR) and q moving average (MA) terms. An additional d order (I) might be introduced if the original series must be differentiated to make it stationary, thus leading to an ARIMA (p, d, q) model. The Box–Jenkins procedure is a schematic and standard method of determining the correct p and q terms, thereby evaluating which is the most adequate model among the ARIMA family models to properly describe the generating process of the studied time series. It consists of three main steps:
-
1.
Model identification: mainly based on the analysis of the series ACF (auto-correlation function) and PACF (partial auto-correlation function). Since pure AR and MA processes have distinctive characteristics in both their respective ACF and PACF, the goal is to recognize in the ACF and PACF of the actual series patterns that are attributable to specific AR and/or MA processes.
-
2.
Model estimation: the method used in this study for determining the parameters in (1) is a nonlinear least square estimate. Most of the dedicated statistics software packages use nonlinear least square or maximum likelihood estimations.
-
3.
Model validation: the series of residuals (that is the series of the errors calculated as the difference between the actual and fitted values) generated by the execution of the model is expected to be equivalent to a white noise process with constant mean and variance. If diagnostic tests show that these assumptions are not verified, it is expected to rerun the model identification step and find a more suitable model.
For a complete and more thorough description of the Box and Jenkins procedure, see for reference Box and Jenkins (1976), Box et al. (1994) and Bourbounnais (2005). Relatively to the Stromboli case study, the estimation procedure led to the selection of a pure auto-regressive process of order 16 (AR16) as a suitable model for fitting the GBInSAR displacement data (2) and performing forecasts:
where the parameters are those defined in (1).
3.3 Definition of probabilistic thresholds and anomalies
With the aim of performing a back-analysis of the displacements, one-step-ahead (i.e., daily) forecasts were sequentially performed at each point of the time series according to Eq. (2) (except for the first year of the dataset, needed as “calibration” period for the model). One fundamental aspect of the ARIMA family models relies on their ability to provide confidence intervals for the forecasts. Assuming that the model is correctly specified, the residuals are random values whose distribution can be represented as a Gaussian curve. Therefore, the variability of forecasts can be measured by a forecast standard error (σ). It follows that the probability of the future actual measurement to fall inside the ±2σ range of the respective forecast is approximately 95 %. Initially, the σ of the forecasts for the Stromboli time series is not constant over time, but is slowly increasing. It becomes steady only after the first unrest period, that is, when the series has displayed his characteristic amplitude of oscillation. For this reason, it was decided to employ an averaged and fixed σ: the interquartile average of the complete series of σ calculated after the first crisis was chosen as a constant confidence interval for the forecasts made over the reference time frame of the study. As a consequence of the one-step-ahead forecasting process, a four-column output was obtained with the following information made available for each day of the time series:
-
actual displacement;
-
forecasted displacement;
-
two “thresholds” of displacement (equal to forecast ± 2σ).
When the actual displacement exceeds the lower displacement threshold (i.e., forecast −2σ), an “anomaly” is found. In fact, since only the inflation pulses of the crater terrace (which is by far the dominant process during unrest phases at Stromboli volcano) are of interest, only the lower bound of the aforementioned confidence interval was considered for detecting anomalous deformation. An anomaly is thus equivalent to the difference between actual displacement and model threshold and is considered an event of inflation of the Stromboli crater terrace which was not consistent with its normal deformation behavior. Contrariwise, when the actual displacement is lower than the respective threshold provided by the model, the amount of anomalous deformation was set to 0. The detected anomalies were both examined in terms of their distribution with time and also normalized with respect to the highest anomaly in the dataset in order to get a better understanding of their intensity. This allowed the identification and characterization of the most intense phases of anomalous deformation.
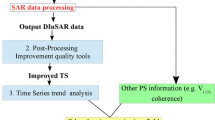
The methodology is summarized in the flowchart of Fig. 2: the GBInSAR displacement time series was fitted with an ARIMA-type model defined through the Box–Jenkins estimation procedure. A time series of predicted displacements was thus generated along with the confidence interval for each forecast, allowing for the comparison with the respective actual measurements. Anomalies were detected when the measured daily inflation of the crater terrace exceeded the respective model threshold, which was defined as forecast −2σ. Finally, through the analysis of the frequency and intensity of the anomalies, the trend of anomalous deformation with time was determined and related to the three unrest phases of Stromboli volcano between January 2010 and August 2014 (Sect. 2).
4 Results
4.1 Analysis of anomalies
The anomalous deformation of the crater terrace was analyzed, considering running time windows of different length. Since periods of inflation and of intense volcanic activity at Stromboli typically last for no more than 3–4 months (Aiuppa et al. 2011; Calvari et al. 2014; Di Traglia et al. 2014b), anomalies were cumulated over running time windows of 7, 30 and 60 days (Fig. 3). As a result, it can be observed that the rate of anomalous deformation during the preparatory phase of the August–November 2014 flank eruption is significantly higher than the rates obtained during the whole 2011 and 2012–2013 minor unrest phases. This is mostly evident by looking at the 60-day curve: on August 5, 2014, a peak of more than 32 mm of anomalous deformation over 60 days is displayed, whereas across the two previous unrest phases a maximum of ~18 mm of anomalous deformation over 60 days can be appreciated. Concerning the 7- and 30-day curves, the peculiarity of the 2014 major unrest phase, although less evident, is still clearly present. Peak values of ~4, ~5.5, ~7.5 mm of anomalous deformation over 7 days and of ~11, ~14, ~21.5 mm of anomalous deformation over 30 days characterize the 2011, 2012–2013 and 2014 unrest phases, respectively. It is also important to note that the model generates a very limited amount of anomalous ground deformation during quiet intervals of volcanic activity (background activity), thus providing no false alarms.
Anomalous ground deformation cumulated over running time windows of 7, 30 and 60 days from early 2011 to the onset of the flank eruption on August 7, 2014. Red triangles mark days characterized by intense volcanic activity (i.e., overflows, strong spattering, powerful explosions, flank eruptions). The colored boxes comprise the time intervals defined in Fig. 1 and Sect. 3.1
4.2 Analysis of normalized anomalies
As mentioned, the normalization was simply performed by dividing each anomaly by the greatest value of daily anomalous deformation detected in the dataset. The following classes were created to classify the anomalies based on their intensity:
-
(a)
normalized anomalies >0
-
(b)
normalized anomalies >0.2
-
(c)
normalized anomalies >0.4
Since the largest difference in peaks of cumulated anomalous deformation was achieved considering a 60-day running time window, the same reference interval was used for the analysis of the normalized anomalies. Figure 4 shows that the preparatory phase of the August 2014 flank eruption was characterized not only by the most amount of cumulative anomalous deformation (Fig. 3), but also by the largest number of anomalies. This is particularly evident for classes b and c. Periods of normal background activity are featured by much fewer anomalies. In particular, chart shows that:
Number of normalized anomalies counted over a 60-day running time window from early 2011 to the onset of the flank eruption on August 7, 2014. Red triangles mark days characterized by intense volcanic activity (i.e., overflows, strong spattering, powerful explosions, flank eruptions). Boxes comprise the time intervals defined in Fig. 1 and Sect. 3.1
-
the largest number of anomalies (46 in 60 days) is relative to the 2014 major unrest phase, just prior to the onset of the flank eruption on August 7, 2014;
-
while the number of low-intensity anomalies (class a) is fairly similar concerning the 2012–2013 and 2014 unrest phases, with regard to the higher-intensity classes (b and c) the difference is noticeably larger (Fig. 4). This suggests that, prior to the flank eruption, the crater terrace was characterized by the most intense pulses of inflation as well.
5 Discussion
Defining the intensity of unrest phases is of crucial importance for volcanic hazard mitigation and eruption management. The use of forecasting methods and the definition of warning thresholds are both activities constituting early warning systems (Intrieri et al. 2013b). Short-term event forecasting is mainly based on deterministic approaches (Voight 1988, 1989; Voight and Cornelius 1991). One of the most known is probably Voight’s (1988, 1989), who finds a relation based on Saito’s (1969) inverse velocity method in order to determine the time of failure of rock slopes and uses it to forecast, in retrospect, the eruption of Mt. St. Helens. However, Voight’s method can only be applied during the terminal stage of failure (Voight 1988); its hypothetical assumption of constant stress conditions and the use of empirical parameters (called A and α) also limit its application as a real operational tool. An alternative approach is probabilistic, which introduce a method to quantify the volcanic hazard and risk (e.g., Newhall and Hoblitt 2002; Marzocchi et al. 2008; Sobradelo et al. 2014). Probabilistic approaches are mainly based on the so-called event tree (Newhall and Hoblitt 2002), a tree graph representation of events in the form of nodes (steps) and branches (outcomes for that particular category). The objective of probabilistic approaches is to outline all the relevant possible outcomes of volcanic unrest, assessing the probability of each hazard scenario occurring within a specified future time interval (Sobradelo et al. 2014). Recent researches on probabilistic evaluation of volcanic scenarios (e.g., Sobradelo et al. 2014) include “a priori” the capacity to differentiate the origin of the precursory signals recorded by the monitoring network. This would imply that a rigorous threshold definition between the background and unrest activity is crucial not only for short-term event forecast, but also for long-term probabilistic approaches. Different methods were proposed for the definitions of warning thresholds from displacement data (Crosta and Agliardi 2002). This can be a challenging task and not rarely raises uncertainties in predicting the evolution of the studied phenomenon. Often methodical procedures to set warning thresholds are lacking and are identified on empirical basis. Cigna et al. (2012) developed a method for the definition of thresholds of displacement, reportedly also usable for volcanoes. However, this is strongly based on the arbitrary choice of the calibration period for which a linear trend must be assumed. Moreover, it does not provide a probabilistic reliability. At Stromboli, warning thresholds were proposed by Ripepe et al. (2009), Inguaggiato et al. (2011) and Di Traglia et al. (2014b), based on observed recordings of geophysical/geochemical data. Coppola et al. (2012) used Moderate Resolution Imaging Spectroradiometer (MODIS) data, classified using a rank ordered statistical plot. To the best of our knowledge, these are the only works where thresholds between background activity and unrest were defined for Stromboli volcano. In general, the impossibility to predict with different degrees of confidence the evolution of the phenomenon under investigation leaves scientific and administrative competent bodies exposed to internal indecision and external criticism.
The statistical approach proposed here for the analysis of the displacement time series of the Stromboli crater terrace is descriptive of the state of activity of the volcano and can be employed during both background and unrest phases. It is based on the concept that monitoring data can be compared to displacements predicted by numerical models in order to identify and quantify anomalous ground deformation (Newcomen and Dick 2015). Stromboli volcano offers a suitable test site for this approach, mainly because the availability of a long and complete dataset of the displacements facilitates the application of the Box–Jenkins procedure for ARIMA model estimation. The structure of the ARIMA models implies that they are particularly sensitive to sudden accelerations in the time series (unless these are related to precise seasonal cycles) rather than to long-term trend variations. Therefore, in the case of Stromboli what the model identifies as an anomaly reflects the occurrence of an abrupt inflation pulse of the crater terrace. It follows that more information is provided beyond the simple qualitative analysis of the trends of daily and cumulative displacement and a quantitative, statistically based description, and classification of the single small-scale pulses of inflation is produced.
The ability to characterize background activity and unrest is even more important when monitoring persistently active volcanoes. In the case of Stromboli, a precise, well-accepted definition of what parameters and activity must be observed to declare the onset of an unrest and to evaluate its intensity still does not exist. Furthermore, a major source of risk at Stromboli is that unrest phases can occasionally evolve into a flank eruption. No evident difference was detected between the style of the inflation that preceded the opening of ephemeral vents at the base of the crater terrace in August 2014, with the subsequent onset of a flank eruption (which can trigger gravitational collapses and tsunamis) and the style of the inflations during the minor unrest phases in 2011 and 2012–2013 (Fig. 1). In fact, the trends of daily displacement of the crater terrace in the last three unrest phases were extremely similar (Fig. 1). Moreover, the total amount of cumulative displacement was actually larger in the 2012–2013 minor unrest than in the preparatory phase of the 2014 flank eruption (Fig. 1).
The results of the ARIMA-based analysis methodology described in Sect. 3 show that anomalies started to occur before all periods characterized by intense volcanic activity (overflows, strong spattering, powerful explosions, flank eruptions), providing no false alarms during quiet time intervals of normal background activity (Figs. 3, 4). Although this gives support to the validity of the method, introducing an arbitrary threshold of anomalous deformation of the crater terrace between background activity and unrest would just push this issue into a different parameter with respect to those proposed already by several authors (Aiuppa et al. 2009; Casagli et al. 2007; Ripepe et al. 2009; Aiuppa et al. 2011; Inguaggiato et al. 2011; Coppola et al. 2012; Calvari et al. 2014; Di Traglia et al. 2014b). More significantly, evident differences were produced concerning the characteristics of the crater terrace inflation during the three periods of volcanic unrest. In fact, the trend of anomalous deformation relative to the 2014 major unrest substantially differs from the trends of anomalous deformation relative to the 2011 and 2012–2013 minor unrests. The preparatory phase of the 2014 flank eruption was characterized by both a larger amount of anomalous deformation and a higher number of anomalies. Specifically, just 2 days before the onset of the flank eruption on August 7, 2014, the crater terrace reached a state where the amount of anomalous deformation cumulated for the previous 60 days was equal to ~32 mm (Fig. 3), nearly doubling the maximum values obtained along the previous unrest phases (~18 mm/60 days). Of the anomalies that ultimately composed these 32 mm, many were of strong intensity (Fig. 4). Considering again a 60-day running time window, 25 anomalies of class b and 13 anomalies of class c anticipated the onset of the flank eruption. Conversely, a maximum of 13 anomalies of class b and 5 anomalies of class c over 60 days occurred during the 2012–2013 minor unrest phase. Even fewer anomalies occurred during the 2011 minor unrest phase.
Given that a limited number of unrest phases characterize the dataset (a total of 3, of which only one major unrest), it is currently not convenient to propose a fixed and arbitrary threshold of anomalous deformation between minor unrest (i.e., not leading to a flank eruption) and major unrest (i.e., leading to a flank eruption) at Stromboli. Moreover, it is probable that this arbitrary threshold would not be applicable to other volcanoes or even other time periods at Stromboli when the underlying magmatic system may have a different configuration. Nonetheless, the trend of anomalous deformation between early 2011 and August 2014 permits to clearly recognize in retrospect the greater intensity of the unrest phase which anticipated the onset of the flank eruption on August 7, 2014. The methodology promises therefore to provide crucial information concerning the intensity of future unrest phases and the prediction of flank eruptions at Stromboli. Being based on a generic approach for the analysis of time series, the former is also suitable to be tested on case studies similar to Stromboli.
6 Conclusions
An innovative statistical approach which makes use of ARIMA models has been applied to the displacement time series of the crater terrace at Stromboli volcano in order to discriminate, in retrospect, the intensity of three phases of inflation. The methodology consisted in comparing the series of actual measurements with a series of one-step-ahead forecasts and in individuating when the measured displacements exceeded a fixed probability threshold for the forecasts (~95 %). The analysis of such occurrences (named “anomalies”) highlighted significant differences in the trends of anomalous deformation between background activity and unrest and, more importantly, also between an unrest phase that culminated into a flank eruption and two that did not.
Data can be updated every time a new measurement is added to the time series (i.e., daily in the case of Stromboli). Therefore, measurements from the GBInSAR system can provide probabilistic daily estimates on the state of anomalous deformation of the crater terrace. The trend of the anomalies can then be compared to the results obtained for previous unrest phases, in order to verify whether the intensity of the inflation is consistent with the onset of a flank eruption. The ability to predict whether summit activity will likely evolve into a flank eruption is in fact a crucial point for the purposes of civil protection planning at Stromboli, since in the past flank eruptions have triggered landslides that reached the sea and generated tsunami sequences. The methodology is generic and theoretically exportable. Assumed the availability of a long and complete dataset, its suitability for the analysis of the displacements from case studies similar to Stromboli can be tested.
References
Aiuppa A et al (2009) The 2007 eruption of Stromboli volcano: insights from real-time measurement of the volcanic gas plume CO2/SO2 ratio. J Volcanol Geotherm Res 182(3–4):221–230
Aiuppa A et al (2011) First observational evidence for the CO2-driven origin of Stromboli’s major explosions. Solid Earth 2(2):135–142
Antonello G, Casagli N, Farina P, Leva D, Nico G, Sieber AJ, Tarchi D (2004) Ground-based SAR interferometry for monitoring mass movements. Landslides 1(1):21–28
Baldi P et al (2008) High precision photogrammetry for monitoring the evolution of the NW flank of Stromboli volcano during and after the 2002–2003 eruption. Bull Volcanol 70:703–715
Barberi F et al (1993) Volcanic hazard assessment at Stromboli based on review of historical data. Acta Vulcanol 3:173–187
Barla G et al (2010) Monitoring of the Beauregard landslide (Aosta Valley, Italy) using advanced and conventional techniques. Eng Geol 116:218–235
Bertagnini A, Landi P (1996) The Secche di Lazzaro pyroclastics of Stromboli volcano: a phreatomagmatic eruption related to the Sciara del Fuoco sector collapse. Bull Volcanol 58:239–245
Blackburn EA, Wilson L, Sparks RSJ (1976) Mechanisms and dynamics of Strombolian activity. J Geol Soc Lond 132:429–440
Bonaccorso A et al (2003) Dynamics of the December 2002 flank failure and tsunami at Stromboli volcano inferred by volcanological and geophysical observations. Geophys Res Lett 30(18):1941–1948
Bourbounnais R (2005) Econométrie, 6th edn. Dunod, Paris
Box GEP, Jenkins GM (1976) Time series analysis: forecasting and control. Holden-Day, San Francisco
Box GEP, Jenkins GM, Reinsel GC (1994) Time series analysis: forecasting and control, 3rd edn. Prentice Hall, Englewood Cliffs, pp 197–199
Calvari S et al (2014) Major eruptive style changes induced by structural modifications of a shallow conduit system: the 2007–2012 Stromboli case. Bull Volcanol 76:841
Calvari S et al (2016) Monitoring crater-wall collapse at active volcanoes: a study of the 12 January 2013 event at Stromboli. Bull Volcanol 78:1–16
Casagli N et al (2007) Deformation of Stromboli Volcano (Italy) during the 2007 crisis by radar interferometry, numerical modeling and field structural data. J Volcanol Geotherm Res 182:182
Cigna F, Tapete D, Casagli N (2012) Semi-automated extraction of Deviation Indexes (DI) from satellite Persistent Scatterers time series: tests on sedimentary volcanism and tectonically-induced motions. Nonlinear Process Geophys 19:643–655
Coppola D et al (2012) “Radiative heat power at Stromboli volcano during 2000–2011: twelve years of MODIS observations. J Volcanol Geotherm Res 215–216:48–60
Crosta GB, Agliardi F (2002) How to obtain alert velocity thresholds for large rockslides. Phys Chem Earth Parts A/B/C 27:1557–1565
D’Oriano C, Bertagnini A, Pompilio M (2011) Ash erupted during normal activity at Stromboli (Aeolian Islands, Italy) raises questions on how the feeding system works. Bull Volcanol 73(5):471–477
Di Roberto A et al (2008) Deep water gravity core from the Marsili Basin (Tyrrhenian Sea) records Pleistocenic-Holocenic explosive events and instability of the Aeolian Archipelago (Italy). J Volcanol Geotherm Res 177:133–144
Di Traglia F, Del Ventisette C, Rosi M, Mugnai F, Intrieri E, Moretti S, Casagli N (2013) Ground-based InSAR reveals conduit pressurization pulses at Stromboli volcano. Terra Nova 25(3):192–198
Di Traglia F et al (2014a) The ground-based InSAR monitoring system at Stromboli volcano: linking changes in displacement rate and intensity of persistent volcanic activity. Bull Volcanol 76:786–803
Di Traglia F et al (2014b) Review of ten years of volcano deformations recorded by the ground-based InSAR monitoring system at Stromboli volcano: a tool to mitigate volcano flank dynamics and intense volcanic activity. Earth Sci Rev 139:317–335
Di Traglia F et al (2014c) Decrypting geophysical signals at Stromboli Volcano (Italy): integration of seismic and Ground-Based InSAR displacement data. Geophys Res Lett 41(8):2753–2761
Di Traglia F, Battaglia M, Nolesini T, Lagomarsino D, Casagli N (2015) Shifts in the eruptive styles at Stromboli in 2010-2014 revealed by ground-based InSAR data. Sci Rep. doi:10.1038/srep13569
Faruk DO (2010) A hybrid neural network and ARIMA model for water quality time series prediction. Eng Appl Artif Intell 23:586–594
Gauthier PJ, Condomines M (1999) 210Pb–226Ra radioactive disequilibria in recent lavas and radon degassing: inferences on the magma chamber dynamics at Stromboli and Merapi volcanoes. Earth Planet Sci Lett 172:111–126
Gauthier PJ, Le Cloarec MF, Condomines M (2000) Degassing processes at Stromboli volcano inferred from short-lived disequilibria (210Pb–210Bi–210Po) in volcanic gases. J Volcanol Geotherm Res 102:1–19
Harris A, Ripepe M (2007) Temperature and dynamics of degassing at Stromboli. J Geophys Res 112:B03205. doi:10.1029/2006JB004393
Inguaggiato S, Vita F, Rouwet D, Bobrowski N, Morici S, Sollami A (2011) Geochemical evidence of the renewal of volcanic activity inferred from CO2 soil and SO2 plume fluxes: the 2007 Stromboli eruption (Italy). Bull Volcanol 73(4):443–456
Intrieri E, Di Traglia F, Del Ventisette C, Gigli G, Mugnai F, Luzi G, Casagli N (2013a) Flank instability of Stromboli volcano (Aeolian Islands, Southern Italy): integration of GB-InSAR and geomorphological observations. Geomorphology 201:60–69
Intrieri E, Gigli G, Casagli N, Nadim F (2013b) Brief communication—Landslide early warning system: toolbox and general concepts. Nat Hazards Earth Syst Sci 13:85–90
Intrieri E et al (2015) Sinkhole monitoring and early warning: an experimental and successful GB-InSAR application. Geomorphology 241:304–314
Lautze NC, Houghton BF (2005) Physical mingling of magma and complex eruption dynamics in the shallow conduit at Stromboli volcano, Italy. Geology 33:425–428
Lautze NC, Houghton BF (2007) “Linking variable explosion style and magma textures during 2002 at Stromboli volcano, Italy. Bull Volcanol 69(4):445–460
Luzi G et al (2004) Ground-based radar interferometry for landslides monitoring: atmospheric and instrumental decorrelation sources on experimental data. IEEE Trans Geosci Remote Sens 42:2454–2466
Luzi G, Monserrat O, Crosetto M, Copons R, Altimir J (2010) Ground-based SAR interferometry applied to landslide monitoring in mountainous areas. In: International conference on “mountain risks: bringing science to society”, 24–26 November 2010, Firenze, Italy
Marzocchi W, Sandri L, Selva J (2008) BET_EF: a probabilistic tool for long-and short-term eruption forecasting. Bull Volcanol 70(5):623–632
Mercalli G (1881) Natura nelle eruzioni dello Stromboli ed in generale dell’attività sismo-vulcanica delle Isole Eolie. Atti Soc It Sci Nat 24:105–134
Neri M et al (2008) Dyke emplacement and related hazard in volcanoes with sector collapse: the 2007 Stromboli (Italy) eruption. J Geol Soc 165:883–886
Newcomen W, Dick G (2015) An update to strain-based pit wall failure prediction method and a justification for slope monitoring. Proc Slope Stab 2015:139–150
Newhall CG, Dzurisin D (1988) Historical unrest at large calderas of the world. US Geol Surv Bull 1–2:1–1108
Newhall C, Hoblitt R (2002) Constructing event trees for volcanic crises. Bull Volcanol 64(1):3–20
Nolesini T, Di Traglia F, Del Ventisette C, Moretti S, Casagli N (2013) Deformations and slope instability on Stromboli volcano: integration of GBInSAR data and analog modeling. Geomorphology 180:242–254
Patrick MR, Harris AJL, Ripepe M, Dehn J, Rothery DA, Calvari S (2007) Strombolian explosive styles and source conditions: insights from thermal (FLIR) video. Bull Volcanol 69(7):769–784
Petrone CM et al (2009) Understanding the collapse-eruption link at Stromboli, Italy: a microanalytical study on the products of the recent Secche di Lazzaro phreatomagmatic activity. J Volcanol Geotherm Res 188:315–332
Pinel V, Poland MP, Hooper A (2014) Volcanology: lessons learned from synthetic aperture radar imagery. J Volcanol Geotherm Res 289:81–113
Potter SH, Scott BJ, Jolly GE, Neall VE, Johnston DM (2015) Introducing the Volcanic Unrest Index (VUI): a tool to quantify and communicate the intensity of volcanic unrest. Bull Volcanol. doi:10.1007/s00445-015-0957-4
Rajesh GK, Krithika S (2009) Day-ahead wind speed forecasting using f-ARIMA models. Renew Energy 34(5):1388–1393
Ripepe M, Delle Donne D, Lacanna G, Marchetti E, Ulivieri G (2009) The onset of the 2007 Stromboli effusive eruption recorded by an integrated geophysical network. J Volcanol Geotherm Res 182:131–136
Rizzo AL et al (2015) The 2014 effusive eruption at Stromboli volcano (Italy): inferences from soil CO2 flux and 3He/4He ratio in thermal waters. Geophys Res Lett 42(7):2235–2243
Rosi M et al (2013) Stromboli Volcano, Aeolian Islands (Italy): present eruptive activity and hazard. In: Lucchi F et al (ed) J Geol Soc London Mem, vol 37, pp 473–490
Rudolf H et al (1999) A mobile and versatile SAR system. In: Proceedings of Geoscience and Remote Sensing Symposium, IGARSS 1999, Hamburg, pp 592–594
Saito M (1969) Forecasting time of slope failure by tertiary creep. In: Proceedings of 7th international conference on soil mechanics foundation engineering, vol 2, pp 677–683
Sobradelo R, Bartolini S, Martí J (2014) HASSET: a probability event tree tool to evaluate future volcanic scenarios using Bayesian inference. Bull Volcanol 76:770–785
Tibaldi A (2001) Multiple sector collapses at Stromboli volcano, Italy: how they work. Bull Volcanol 63:112–125
Tinti S et al (2006a) Observations of physical effects from tsunamis of December 30, 2002 at Stromboli volcano, southern Italy. Bull Volcanol 68:450–461
Tinti S et al (2006b) The landslides and tsunamis of the 30th of December, 2002 in Stromboli analysed through numerical simulations. Bull Volcanol 68:462–479
Van der Voort M, Dougherty M, Watson S (1996) Combining Kohonen maps with ARIMA time series models to forecast traffic flow. Transp Res C 4(5):307–318
Voight B (1988) A method for prediction of volcanic eruption. Nature 332(10):125–130
Voight B (1989) A relation to describe rate-dependent material failure. Science 243(4888):200–203
Voight B, Cornelius RR (1991) Prospects for eruption prediction in near real-time. Nature 350(6320):695–698
Wadge G et al (2008) Lava dome growth and mass wasting measured by a time series of ground‐based radar and seismicity observations. J Geoph Res 113:B08210. doi:10.1029/2007JB005466
Wadge G et al (2014) AVTIS observations of lava dome growth at Soufrière Hills Volcano, Montserrat: 2004 to 2011. Geol Soc Lond Mem 39(1):229–240
Zebker HA, Rosen PA, Hensley S (1997) Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J Geophys Res 102(B4):7547–7563
Acknowledgments
The authors wish to thank two anonymous reviewers for their precious comments and suggestions. This work has been financially supported by the “Presidenza del Consiglio dei Ministri—Dipartimento della Protezione Civile” (Presidency of the Council of Ministers—Department of Civil Protection) within the framework of the SAR.net, SAR.net2, InGrID and InGrID2015 projects; this publication, however, does not reflect the position and the official policies of the department. Data and sensor used are designed and produced by Ellegi LLC using proprietary GBInSAR technology by LiSALab LLC, a European Commission Joint Research Centre spin-off.
Contributions
All authors contributed extensively to the work presented in this manuscript. T.C. and E.I. conceived the study and performed the calculations. F.D.T. provided reference volcanic data for calibration of the model and analyzed the data. Each author contributed to the manuscript writing. In details:
-
Tommaso Carlà: conception and realization of the manuscript, GBInSAR data analysis and modeling.
-
Emanuele Intrieri: conception and realization of the manuscript, GBInSAR data analysis and modeling.
-
Federico Di Traglia: conception and realization of the manuscript, GBInSAR data analysis, field validation, GBInSAR maintenance.
-
Nicola Casagli: realization of the manuscript, financial support, responsible of the SAR.net, SAR.net2, InGrID and InGrID2015 projects.
Author information
Authors and Affiliations
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Carlà, T., Intrieri, E., Di Traglia, F. et al. A statistical-based approach for determining the intensity of unrest phases at Stromboli volcano (Southern Italy) using one-step-ahead forecasts of displacement time series. Nat Hazards 84, 669–683 (2016). https://doi.org/10.1007/s11069-016-2451-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-016-2451-5