A multivariate generalized linear tsunami fragility model for Kesennuma City based on maximum flow depths, velocities and debris impact, with evaluation of predictive accuracy

Abstract

The recent losses caused by the unprecedented 2011 Great East Japan Tsunami disaster have stimulated further research efforts, notably in the mechanisms and probabilistic determination of tsunami-induced damage, in order to provide the necessary information for future risk assessment and mitigation. The stochastic approach typically adopts fragility functions, which express the probability that a building will reach or exceed a predefined damage level usually for one, sometimes several measures of tsunami intensity. However, improvements in the derivation of fragility functions are still needed in order to yield reliable predictions of tsunami damage to buildings. In particular, extensive disaggregated databases, as well as measures of tsunami intensity beyond the commonly used tsunami flow depth should be used to potentially capture variations in the data which have not been explained by previous models. This study proposes to derive fragility functions with additional intensity measures for the city of Kesennuma, which was extensively damaged during the 2011 tsunami and for which a large and disaggregated dataset of building damage is available. In addition to the surveyed tsunami flow depth, the numerically estimated flow velocities as well as a binary indicator of debris impact are included in the model and used simultaneously to estimate building damage probabilities. Following the recently proposed methodology for fragility estimation based on generalized linear models, which overcomes the shortcomings of classic linear regression in fragility analyses, ordinal regression is applied and the reliability of the model estimates is assessed using a proposed penalized accuracy measure, more suitable than the traditional classification error rate for ordinal models. In order to assess the predictive power of the model, penalized accuracy is estimated through a repeated tenfold cross-validation scheme. For the first time, multivariate tsunami fragility functions are derived and represented in the form of fragility surfaces. The results show that the model is able to predict tsunami damage with satisfactory predictive accuracy and that debris impact is a crucial factor in the determination of building collapse probabilities.

Introduction

The widespread destruction caused by the 2011 Great East Japan tsunami has demonstrated that even state-of-the-art coastal protection measures and disaster mitigation strategies, in countries such as Japan, cannot prevent large tsunamis from causing severe large-scale building damage, thus significant economical losses and loss of life. In order to provide better tools to decision makers, engineers and the risk assessment community in exposed countries, it is necessary to further our understanding of structural failure mechanisms under tsunami loads and to improve the predictive ability of current models to estimate future potential tsunami damage. While from a deterministic standpoint some noticeable advancements are being made on the identification of wave inundation processes and actions of tsunami forces, from both large-scale hydraulic experiments (Arikawa 2009; Arnasson et al. 2009; Charvet et al. 2013a; Lloyd 2014), field surveys (Chock et al. 2013; EEFIT 2013), as well as simulation with particle–fluid mixture flows (Pudasaini 2014), from a probabilistic perspective the likelihood of future tsunami-induced building damage, or fragility estimation, still requires considerable improvements in order to reduce the uncertainty associated with the predictions (Suppasri et al. 2013a; Charvet et al. 2014a, b). Fragility estimations are obtained through the derivation of fragility functions, which are empirical stochastic functions giving the probability that a building will reach or exceed a given level of damage for a measure of tsunami intensity (IM). Damage levels are typically defined prior to a post-tsunami survey by engineering teams and describe the condition of the affected structure, from zero damage to complete failure, thus forming a damage scale. Such scale is then used in combination with tsunami flow depth measurements (Ruangrassamee et al. 2006; Mas et al. 2012; Suppasri et al. 2012a, 2013a, b) or results from numerical simulations (Koshimura et al. 2009; Suppasri et al. 2011, 2012b) in order to classify the surveyed buildings according to their damage state and a corresponding IM. The first column of Table 1 presents the damage scale defined by the Ministry of Land, Infrastructure, Transport and Tourism in Japan (MLIT) for the survey of the buildings affected by the Great East Japan tsunami that struck the country on March, 11, 2011.

Table 1 Tsunami damage scale defined by the ministry of land, infrastructure and transport and tourism in Japan

Fragility functions are derived by applying regression analysis techniques to the classified observations, using damage state as response variable and the chosen IM (most commonly the tsunami flow depth—e.g., Suppasri et al. 2013a, b; in some cases numerically estimated flow velocities, or analytically estimated hydrodynamic forces—e.g., Suppasri et al. 2012b) as the explanatory variable. Typically, fragility functions are derived by using linear least squares regression, assuming that the response to be modeled follows a normal or lognormal distribution, and by grouping or re-regrouping the data into bins of tsunami intensity (e.g., Suppasri et al. 2011, 2012a) Nevertheless, it was shown by Charvet et al. (2013b) and Charvet et al. (2014a, b) that considerable uncertainty was introduced in the damage predictions when such methods are used as a tool to analyze building damage data. The results from Charvet et al. (2014a) also indicate that highly aggregated databases (i.e., when observations are grouped into a range of tsunami IM, and/or grouped over a wide range of geographical locations) result in a loss of information, potentially yielding variations which cannot be explained by the model. The building damage analysis following the 2009 Samoa tsunami by Reese et al. (2011) was the first study in the tsunami engineering field which derived fragility functions using a more adequate statistical approach, namely logistic regression, assuming the damage response to follow a binomial distribution (i.e., damaged/not damaged). However, logistic regression does not exploit fully the information available in the database, as it ignores the fact that damage is an ordinal categorical variable.

In order to address such issues, Charvet et al. (2014b) used ordinal regression analysis using the extensive disaggregated database (56950 individual buildings) from Ishinomaki city in Japan, one of the most severely affected cities during the 2011 Great East Japan tsunami. Ordinal regression is a statistical method based on the use of Generalized Linear Models, or GLM (Mc Cullagh and Nelder 1989). GLM relax many of the assumptions associated with linear least squares regression, thus addressing a number of issues associated with this method (more details can be found in Charvet et al. 2014a, b). In addition, they allow the response variable (i.e., damage state) to follow a number of statistical distributions, including discrete distributions (more adequate to describe the discrete nature of the damage states). However, despite the use of a detailed database and a more elaborate statistical estimation method, Charvet et al. (2014b) found that the model still did not capture all the systematic variability in the data, particularly for high damage states. In addition, for the strongest construction types such as RC (Reinforced Concrete) and Steel buildings, the data were heavily scattered, showing that the chosen IM alone (i.e., flow depth) is a poor predictor of damage for these structures. Therefore, it has become more and more apparent that at least a large proportion of the uncertainty associated with fragility estimations could be reduced by incorporating in the model explanatory variables beyond the commonly used tsunami flow depth. Indeed, there is much visual evidence to support the important contribution of variables such as debris impact and scour to severe damage states, as well as the impact of high flow velocities which can be inferred from the occurrence of building overturn or from the residual deformation of columns (Fig. 1). A number of analytical expressions for tsunami forces exist and are consistent with the ones shown in Fig. 1—taken from FEMA (2008) and Chock et al. (2011). Nevertheless, such dynamical quantities (flow depth and velocities) can better be obtained by applying a real two-phase mass flow model and unified simulation techniques as proposed in Pudasaini (2012, 2014). In addition, variables such as the Froude number (for example, as used in the scour depth estimation in Fig. 1d) are crucial in designing coastal structures and estimating their strength. Therefore, they should be appropriately modeled. When the flow hits the obstacle, the flow is rapidly and largely sheared in the flow depth direction, then turns from shallow to full dimensional. In this situation, a more advanced generalized Froude number (Dominik and Pudasaini 2012) should be used that varies through the flow depth and takes into account several important dynamical aspects of the flow including the gravity and pressure potential energies and the kinetic energy of the flow (Pudasaini and Dominik 2009). Moreover, the Froude number should also include the phase-Froude numbers for solid and fluid as proposed in Pudasaini (2012), which takes into account interactions between the solid and fluid components.

Fig. 1

Characteristic building damage triggered by the 2011 tsunami in Japan, with analytical expression of the tsunami force component(s) identified as the main cause of damage. a Building which has been overturned, due to the combined actions of hydrostatic (lateral and buoyancy forces) and hydrodynamic loads. Such forces are mainly determined by the tsunami flow depth h and the flow velocity u (other parameters are typically taken as constants—FEMA 2008). b Residual deformation of columns due to sustained lateral loads (EEFIT 2013), namely a combination of hydrostatic and hydrodynamic forces (respectively, F _h and F _d ). These two force components always act on the building concurrently, as indicated by the double arrow (a)–(b). Other damaging mechanisms are also at play, such as debris impact (c), and scour (d). In this figure, h is the tsunami flow depth, u is the horizontal flow velocity, ρ _s is the fluid density (accounting for sediment density), g is the acceleration of gravity, b is the breadth of the structure, C _d is the drag coefficient, C _m is the virtual mass coefficient, and u _d is the velocity of the debris. u _d must the relative velocity between the solid and the fluid with the virtual mass coefficient (Pudasaini 2012), k is the effective contact stiffness of the debris object and the impacted system as described in Chock et al. (2011), m is the mass of the debris, z _m is the scour depth, Fr is the Froude number (Hughes 1993), and K _a the approach angle

While flow depth has been found to be a good predictor of tsunami damage for low damage states (Charvet et al. 2014a, b), it is clear that the contribution of such variables will be increasingly important in explaining higher damage states and should be included in the model in order to yield better results (Fig. 2).

Fig. 2

Schematic representation of the contributions of different tsunami intensity measures to the severity of observed damage. In general, the number of influential tsunami IMs increases as well as the contribution of each IM along with the damage level. More specifically, the contribution of flow depth will be more prominent for lower damage states (i.e., DS1: “flooding”), while flow velocity and debris impact will be increasingly influential from non-structural to the heaviest structural damage, and scour corresponding mainly to heavy structural damage states

The choice of flow depth as a unique demand parameter, or explanatory variable, in the construction of fragility curves stems from the fact this measure can be retrieved directly from field surveys (for example, by measuring the height of the water mark on an affected building). Flow velocities, on the other hand, can be used as an IM but require detailed numerical simulations (Mader 2004). Recent advances in phase flow modeling also demonstrate flow height and velocity could better be obtained by applying sophisticated two-phase models such as those proposed by Pudasaini (2012, 2014). Scour is a complex process which depends on factors such as flow approach angle, number of waves, soil conditions (Chock et al. 2011), which are typically not reported or straightforward to identify. For obvious reasons, debris are always removed by the authorities as quickly as possible after a tsunami attack, thus information on their contribution to damage is very difficult to quantify from post-tsunami surveys.

Challenges associated with the inclusion of several variables include the representation of fragility functions in a different form (e.g., more than two dimensions), and a meaningful quantitative assessment of the model’s reliability. In the case of ordinal regression, the latter can be assessed qualitatively through a graphical representation of the expected (model) versus observed (data) probabilities or counts (Charvet et al. 2014a, b). Nevertheless, this graphical tool becomes insufficient as the number of variables increases—indeed, in order for such diagnostics plot to be meaningful each point has to represent a unique combination of values for all explanatory variables. This leads to very low counts of instances (e.g., less than 10) when an increasing number of explanatory variables is included. Furthermore, it would be desirable to provide a quantitative and straightforward measure of predictive ability for ordinal models, instead of a quantitative assessment.

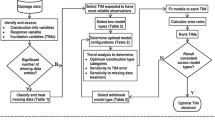
In the light of these findings and considerations, this study aims to perform the building fragility analysis for the city of Kesennuma in Japan, heavily affected by the 2011 tsunami, for which a fully disaggregated damage database, surveyed flow depth measurements and velocity simulation results are available. Due to its adequacy in representing the damage response scale, the statistical method used is ordinal regression, although the adequacy of a more complex, partially ordered model will also be tested. One main objective of this work is to include not only flow depth and the simulated velocities as explanatory variables, but also an indicator of debris impact, based on the geographical location of sources of harmful debris (i.e., washed away structures). The model is built step by step, by considering notably the relative influence of the variables to be included on the response. The predictive power of the model is assessed using a proposed penalized accuracy measure (accounting for the magnitude of the error), and a repeated tenfold cross-validation scheme. Finally, the multivariate fragility functions are represented in the form of fragility surfaces, allowing for an assessment of the influence of debris impact on high damage probabilities and a comparison of the relative fragility of different building classes.

Presentation of the data

Building damage and tsunami flow depth

The building damage dataset was provided by the city of Kesennuma, it contains 19815 individual buildings, and the available information includes the tsunami flow depth retrieved from the post-disaster survey (i.e., maximum tsunami flow depth), for 14760 buildings the main construction material (RC, Steel, Wood or Masonry), and for 9415 buildings the number of stories. Detailed construction practices for each of these main construction classes for Japan can be found in Architectural Institute of Japan (2012). The damage scale that was used to classify the observation is the scale presented in Table 1. The examination of the damage scale designed by the MLIT reveals that DS5 and DS6 do not represent mutually exclusive damage states, nor do they necessarily represent an increase in tsunami intensity. Rather, they represent different failure modes of the structure. In order to apply GLM analysis, Mc Cullagh and Nelder (1989) advise for such requirements to be met; therefore, in this study these two levels will be aggregated (i.e., DS5 will correspond to the buildings that have collapsed, and the ones that have been washed away). This transforms the given seven-state (DS0 to DS6) into a six-state damage scale (DS0 to DS5).

Flow velocities

The flow velocity estimations for Kesennuma are obtained from a nonlinear shallow water model, namely the TUNAMI model. A set of nonlinear shallow water equations is discretized using the Staggered Leap-frog finite difference scheme (Imamura 1996). Bottom friction for urban areas—where the concentration of buildings is significant—can be represented using high Manning’s roughness coefficients values (i.e., 0.04 or higher). In reality, when a building is washed away (a frequent occurrence in this particular event), the friction is reduced dramatically as the site becomes effectively concrete or bare ground. This increases the actual flow velocity over that area, effect which would be missed in the modeling. Therefore, in the absence of land cover models for Kesennuma, a constant Manning’s roughness coefficient of 0.025 was chosen for the present simulation, an avenue for improvement would be to consider friction as a dynamically varying parameter conditional on the washing away of structures (or other significant changes in land cover due to the tsunami flow). The requires the availability of detailed land use land cover data, concurrently with the determination of a washed away state conditional on a set of depth-velocity values.

Five computational domains are used as a nested grid system: 405 m (Region 1), 135 m (Region 2), 45 m (Region 3), 15 m (Region 4) and 5 m (Region 5), as shown in Fig. 3. The bathymetry data for Region 1 were derived from a combination of the original data from the Japan Coast Guard and the Cabinet Office, Government of Japan, Regions 2 to 5 are from the Cabinet Office, Government of Japan. The topography data for Regions 1 to 3 were derived from the Cabinet Office, Government of Japan and from the Geospatial Information Authority of Japan for Regions 4 to 5. All bathymetry and topography data used in this study were collected before the occurrence of the 2011 tsunami. In order to carry out fragility estimations and limit the uncertainty associated with the velocity estimations from coarse grid sizes, this study only uses the buildings located in Region 5 (10812 buildings), for which a 5-m grid size has been used.

Fig. 3

Nested grid system used for the tsunami numerical modeling in the region of Kesennuma

The flow velocity values retrieved from the simulation are maximum estimated flow velocities. Suppasri et al. (2014) used a similar simulation setup (source deformation, wave propagation model), with the exception of a coarser resolution of 135 m for the region of interest (region 5). They found a reasonable agreement between the modeled tsunami flow velocity ranges, and local velocities measured from available survivor videos in Sendai plain (Hayashi and Koshimura 2013) and Kesennuma City (Fritz et al. 2012). However, better simulation of the tsunami velocities can be obtained by utilizing a real two-phase tsunami run-up model and unified simulations (Pudasaini 2014) as the flow is mainly two-phased in nature (processes such as runup and impact on structures).

While it is worth noting that the time of occurrence of maximum depth and maximum flow velocity is not necessarily the same at a given location, it is expected that the final observed damage is a result of successive failures triggered by the overall maximum demands.

Debris impact

A number of tsunami disasters have shown that debris impact can severely damage a structure. Following the 2006 Java tsunami survey, Reese et al. (2007) found robust buildings could act as a shield for weaker buildings, which would have typically suffered heavy damage from impacting debris. In the case of Kesennuma, it was not possible to directly quantify debris impact or the effects of sheltering from post-tsunami surveys, not only because of early debris removal by the authorities, but also because in the case of collapsed or washed away structures clear evidence of debris impact was not available. However, it can be seen (Fig. 4) that the bulk of debris material generated by the 2011 event seems to be composed mainly of the remains of buildings which have been washed away. Thus, in this study we assume that impact will occur if the building under consideration is in the surroundings of a structure which has been washed away (as defined by the damage scale in Table 1) and define such impact as a binary occurrence, i.e., either a building is impacted (debris impact = 1) or not (debris impact = 0). Because the distance travelled by the projectile from the point of debris generation (i.e., initial location of the washed away structure) to the affected building is unknown, a range of debris action radiuses (from 10 m to 150 m) will be tested (Fig. 5), using cross-validation and the accuracy measure presented in the following section.

Fig. 4

Photographic evidence from the immediate tsunami aftermath in Kesennuma, showing the nature of debris generated by the tsunami (a lot of remains from washed away houses)

Fig. 5

Principle of debris impact variable assignment in Kesennuma. If a building is washed away, it is assumed the generated debris can travel a distance of 50 m from this building (for instance), then all buildings located within 50 m of this washed away structure are assigned a value of ‘1’ for debris impact (the other ones are assigned a value of ‘0’)

Fragility estimation methodology

Ordinal regression model

In this study, fragility functions are estimated using GLM, more specifically ordinal regression. The generalized linear models methodology implies firstly, the selection of an appropriate statistical distribution for the response variable (i.e., the damage state), which will be referred to as the random component of the model; secondly, the expression of the damage probability exceedance (or fragility function μ) through a chosen linear predictor η and link function g (this will be referred to as the systematic component). In ordinal regression analysis, the random component chosen is the multinomial distribution (Forbes et al. 2011), a multicategorical discrete distribution, expressed as:

$$Y_{k,i} \sim \mathop \prod \limits_{k = 0}^{K} \frac{{N_{i} !}}{{Y_{k,i} !}}P\left( {DS = ds_{k} |x_{i} } \right)^{{Y_{k,i} }} .$$

(1)

In Eq. (1), Y _k,i corresponds to the counts of buildings being at damage level ds _k $(k \in {\mathbb{N}};0 \le k \le K)$ for each value of the tsunami intensity measure x _i ; and N _i is the total number of buildings. This probability can be transformed into the probability of reaching or exceeding ds _k given x _i , P(DS ≥ ds _k |x _i ), essentially expressing the required fragility function, as:

$$P\left( {DS = ds_{k} |x_{i} } \right) = \left\{ {\begin{array}{*{20}l} {1 - P\left( {DS \ge ds_{k} |x_{i} } \right) \quad k = 0} \hfill \\ {P\left( {DS \ge ds_{k} |x_{i} } \right) - P\left( {DS \ge ds_{k + 1} |x_{i} } \right)\quad 0 < k < K} \hfill \\ {P\left( {DS \ge ds_{k} |x_{i} } \right) \quad k = K} \hfill \\ \end{array} } \right.$$

(2)

When using GLM, the linear predictor is an additive function of all explanatory variables included. Posing P(DS ≥ ds _k ) = μ _k , the linear predictor defines the systematic component of the model as follows:

$$\left( {\left. {\eta_{k} } \right|1 \le k \le K} \right) = g\left( {\mu_{k} } \right) = \theta_{0,k} + \mathop \sum \limits_{j = 1}^{J} \theta_{k,j} X_{j} .$$

(3)

In Eq. (3), X _j are the J explanatory variables that can be used for the regression analysis, and {θ _0,k , …, θ _k,j } are the parameters of the model to be estimated. In the case of Kesennuma city, we have J = 5 explanatory variables: the surveyed tsunami flow depth, the simulated flow velocities, the debris impact (dummy coded as 0 or 1), the building class (Wood, Masonry, RC, or Steel, also dummy coded), and the number of stories (1 to 6, treated as a continuous variable). $e^{{\theta_{k,j| \ne 0} }}$ represents the “odds ratio”. For example, assuming the usual logit function $\left( {\log \left( {\frac{P}{1 - P}} \right)} \right)$ as link for the model, for a given damage class k and explanatory variable X _j the odds that the damage state of a building is above level k are multiplied by $e^{{\theta_{k,j| \ne 0} }}$ for each unit increase in X _j .

Ordinal regression assumes that the response categories are ordered, this is taken into account by fixing the free parameters in the systematic component (3) across all damage states, allowing only the constant θ _0,k to vary, thus (3) becomes:

$$\left( {\left. {\eta_{k} } \right|1 \le k \le K} \right) = g\left( {\mu_{k} } \right) = \theta_{0,k} + \mathop \sum \limits_{j = 1}^{J} \theta_{j} X_{j}$$

(4)

The parameters in (4), the ordered model, are estimated using maximum likelihood estimation or MLE (Mc Cullagh and Nelder 1989; Myung 2003). MLE consists in retrieving the set of parameters which maximizes the probability of the observed data. Note that the ordered model now assumes that the rate of increase in the odds for a unit increase in X _j is constant across the classes (i.e., $\theta_{k,j|j \ne 0}$ becomes $\theta_{j|j \ne 0}$). This parameter estimation method assumes that observed values of the response and explanatory variables were measured without error (i.e., there is no difference between the estimated and true values of the model parameters). In reality, the damage classification of a building (response) is by nature subjective, and the measurement of explanatory variables such as flow depth (in the field) or velocity (numerical modeling approximations) is also subject to uncertainty. In order to address such uncertainty, Bayesian estimation methods can be used, as they allow for measurement errors to be incorporated via appropriate statistical distributions. However, due to the lack of prior information on measurement errors and resulting parameter uncertainty, the use of these more complex methods is unnecessary. Indeed, the use of uninformative priors in Bayesian parameter estimation converges to the MLE result.

Generally, for regression based on binary or multinomial outcomes, the appropriate link functions g are the logit, probit, and in some cases the complementary loglog functions, as described in Rossetto et al. (2014). Note that the complementary loglog link is not considered here, as this link provides estimations close to the logit link except for a heavier right tail; and cannot be differentiated when the linear predictor takes the value of zero.

Diagnostics

Relative goodness-of-fit: deviance and AIC

Measures of relative goodness-of-fit consist in comparing the performance of several possible models, based on the same statistical distribution, but with a different number of parameters or different link functions. When the two models compared use the same link function but have a different number of parameters (i.e., nested models), the likelihood ratio test is appropriate (Fahrmeir and Tutz 2001). It reveals whether the model which has more parameters gives a significantly better fit to the data than its simpler alternative. Thus it is useful to use the likelihood ratio test in order to determine:

• Which IMs have a significant influence on the response. The IMs are added step by step, after systematically checking their usefulness as explanatory variables.

• If interaction terms should be included in the model. When at least 2 IMs are included, there is a possibility that the influence of one IM on the response depends on the value of the other. The interaction term for each combination of IMs is a multiplicative function of those IMs.

• If the assumption of an ordered response does not hold, i.e., if the multinomial model [Eq. (3)], which has more parameters, provides a better fit to the data than its simple, ordinal alternative.

When two models have the same number of parameters and are based on the same statistical distribution of the response, thus differ only by their link function, the Akaike information criterion, or AIC (Akaike 1974) should be used:

$${\text{AIC}} = 2p - 2\log \left( L \right),$$

(5)

In (5), p is the number of parameters in the model, $- 2\log \left( L \right)$ is the model’s deviance, a measure of error and a function of the maximum likelihood L. The best fitting model is the model with the smallest AIC.

Absolute goodness-of-fit: penalized accuracy and cross-validation

Contrary to models fitted using least squares regression and applied to continuous responses which typically use the coefficient of determination (R ²) to assess goodness-of-fit; a common measure of absolute goodness-of-fit of GLM applied to discrete outcomes is the model accuracy (Baldi et al. 2000; Leelawat et al. 2014). Indeed, if some “equivalent” R ² values can theoretically be calculated for generalized linear models, their meaning is significantly different from the classic coefficient of determination used in linear least squares regression (Hu et al. 2006) and the use of such measure in this context is often discouraged (Zheng and Agresti 2000). Accuracy is typically calculated by deducing the classification error rate (i.e., the number of incorrectly classified outcomes) from a perfect model accuracy of 1, or directly (and equivalently) defined as the proportion of well-classified outcomes. In this case, the accuracy acc _i of the model for each individual data point is:

$$acc_{i} = \left\{ { \begin{array}{l} { 1\quad DS_{i} = \widehat{DS}_{i} } \\ {0\quad DS_{i} \ne \widehat{DS}_{i} } \\ \end{array} } \right.$$

(6)

In (6), DS _i is the actual damage state and $\widehat{DS}_{i}$ the damage state estimated from the model output for the ith observation (or expected damage). The overall classifier’s accuracy Acc is typically defined as a percentage, representing the ratio of correctly classified outcomes to the total sample size n:

$$Acc = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} acc_{i}$$

(7)

This measure has the advantage to be easy to calculate and interpret, particularly for binomial models. However, a major shortcoming of accuracy for ordinal models is the fact it does not take into account the ordered nature of the response categories. For example, if a building has been classified as DS4 (field observation) and the model misclassifies this observation as DS3, the error is not as large as if the model had misclassified it as DS1. Unfortunately, typical accuracy calculations only count the number of correctly classified outcomes, so information on the discrepancy between the observed and predicted measures for unsuccessful model estimations is not exploited. It is therefore necessary to include a correction term in the accuracy calculation to obtain more meaningful estimates. The proposed amendment to this approach is to take into account the distance between the observed and predicted classes for each instance in (6). Assuming the classes are equidistant, we adopt a similar approach to that proposed by Rennie and Srebro (2005), by incorporating an immediate-threshold loss function which penalizes the accuracy estimation proportionally to the distance between the observed and predicted outcomes:

$$acc_{i} = 1 - \frac{{\left| {DS_{i} - \widehat{DS}_{i} } \right|}}{K - 1}$$

(8)

The penalized accuracy estimations (8) are then substituted in (7) to obtain the overall penalized accuracy of the ordinal model. Note that because ordinal regression analysis estimates the response probabilities directly, the expected damage state is calculated a posteriori by assuming that $\widehat{DS}_{i}$ is reached or exceeded from a chosen probability threshold (here this threshold is set at 0.5). Thus the accuracy results may vary slightly depending on the threshold chosen.

Finally, in order to avoid the issue of model overfitting (i.e., over-confidence in the results) and give a realistic estimation of future model performance, it is necessary to test the ability of the model to classify correctly unseen data. This can be done by using a repeated cross-validation algorithm, which, in comparison with other estimators such as repeated hold-out and bootstrap, was shown to be an adequate estimator of accuracy (Kohavi 1995) or related classification error rates (Kim 2009). The penalized accuracy estimations presented in the following sections correspond to the cross-validated estimates, derived using repeated tenfold cross-validation.

Results and discussion

Model selection

Following the methodology described in 3.2.1, explanatory variables are added one by one to the ordered systematic component of the GLM [Eq. (4)], as well as possible interaction terms between these variables. At each step, a likelihood ratio test is used to determine whether the added term results in a significantly better fit of the most complex model compared with the simple model. The same test is used to compare the ordered model with an equivalent but more complex, multinomial model [Eq. (3)], which relaxes the assumption that the response categories (i.e., damage states) are ordered.

Two different link functions will be considered: the probit and logit link functions. Because models differing by their link functions are non-nested models, we use the AIC [Eq. (5)] in order to determine which link function provides a better fit to the data.

In this stage of the analysis, the binary debris impact variable has been defined for a radius of projectile action of 50 m. Indeed, this distance is thought to be significant enough for the linear predictor to also contain meaningful variations in measured flow depths and simulated flow velocities, while not being too large, which could increase the uncertainty of whether a building has in reality been impacted or not. Each possible radius is considered individually in the next stage (Sect. 4.2). The variable ‘number of stories’ was treated as a continuous variable.

The results from Tables 2 and 3 indicate that, for both link functions the more complex multinomial model generally does not yield a better fit compared to the ordered model. Thus ordinal regression is an adequate choice for the analysis. A comparison between the AIC values of the best fitting probit model and the best fitting logit model (i.e., 5862 and 5766, respectively) indicates that the logit function leads to a slightly better fit.

Table 2 Deviance and AIC values of the ordered and multinomial probit models. The values in bold represent minimum deviance and AIC values (i.e. the best fitting model)

Table 3 Deviance and AIC values of the ordered and multinomial logit models. The values in bold represent minimum deviance and AIC values (i.e. the best fitting model)

According to the results in Table 3, the explanatory variables to be included in the model [i.e., Eq. (4)] are: the available tsunami IMs (flow depth, flow velocity, debris impact), the building’s construction material, the number of stories; and the interaction terms to be included are interactions between flow depth and velocity (h.v), flow depth and debris impact (h.I), flow velocity and debris impact (v.I), flow depth and building material (h.M), flow velocity and building material (v.M), material and debris impact (M.I), number of stories and flow depth (S.h), number of stories and debris impact (S.I), as well as number of stories and building material (S.M). These findings are consistent with the physical processes at play during tsunami flow-structure interaction. Indeed, although the extent to which maximum flow velocity interacts with maximum flow depth is unknown, it is expected an increase in maximum flow velocity would have an effect on the rate of increase in damage probability which depends on the value of flow depth. Similarly, it is expected that the effects of hydrostatic and hydrodynamic loads (i.e., flow depth and velocity) on increasing damage probabilities will depend on whether the building is also suffering debris impact loads. The same reasoning can be applied for other interaction terms.

Finally, it is interesting to note for both link functions, and aside of significance testing, the largest reductions in model deviance (i.e., more than 1000) result from the addition of building material and number of stories to the initial flow depth as explanatory variables. This result is consistent with previous findings (Suppasri et al. 2013a, b; Leelawat et al. 2014) and indicates that aside from tsunami IMs, the construction characteristics of a building strongly determine the severity of damage. Comparatively, the difference in deviance associated with the inclusion of debris impact and flow velocity is smaller. This can be explained by the uncertainty associated with the determination of both variables, as flow velocity inland was calculated with a constant roughness coefficient and using nonlinear shallow water equations, which may not be perfectly accurate onshore (Charvet 2012) and the debris impact variable is relatively coarse, based on the assumption that debris impact is due to washed away buildings rather than actual individual observations. Nevertheless, these variables still yield significant model improvement (which is consistent with field survey evidence, showing the unquestionable contribution of these IMs to tsunami-induced damage—see Sect. 1, as well as Figs. 1 and 4). It is expected that more dramatic reductions in deviance and AIC will result if refined estimations for these two IMs are obtained in the future.

Penalized accuracy and debris impact radius

In the aftermath of a tsunami attack, and due to the different responses of structures to tsunami loads depending on the building’s construction type, fragility is often represented separately for different building classes. Thus, following the method presented in 3.2.2, the overall penalized accuracy of the model is calculated for each building class and for each debris impact radius (10 m–150 m). The required number of iterations of the repeated cross-validation scheme is determined through the examination of the results’ stability, for a debris impact radius of 50 m. We consider the model is stable when the variability of the penalized accuracy results is in the order of 0.01 % (so no additional iterations are required). Table 4 presents the overall penalized accuracy for each building class and debris impact radius, as well as the number of iterations used. Note that for Steel buildings, the number of stories variable and associated interactions could not be included in the model. Indeed, this information was only available for 12 points in the Steel database, which is not sufficient for the present regression analysis (Green 1991).

Table 4 Overall penalized accuracy of the ordinal model calculated using N repetitions of a tenfold cross-validation algorithm. The values in bold represent the maximum accuracy obtained for each building type

The results in Table 4 show that the model yields a high predictive accuracy (>90 %) for all building classes. This result partly reflects the commonality of heavy damage states (Fig. 6), particularly for Wood and Masonry buildings, for which 85 % and 65 % of the data, respectively, lie in the “collapse” category, making the overall possible loss trivial for potentially misclassified data. However, the model performs reasonably well also with regard to accuracy for Steel and RC structures, for which the damage distributions, while skewed to the left, are more even. It is therefore considered from such results that the predictors and model chosen are adequate to predict building damage probabilities for this event.

Fig. 6

Density histograms representing the distribution of each building material according to the observed damage, a Wood, b Masonry, c RC, d Steel

The highest accuracy for RC buildings is obtained for a debris impact radius of 90 m, for Steel buildings 30 m, for Wood buildings 130 m to 140 m, and for Masonry buildings 120 m. These results appear consistent with the mechanisms of debris action; as the kinetic energy of the flow (as well as the moving debris) will decrease progressively as it travels: Wood and Masonry buildings being the weakest construction types, it is expected that the effects of projectiles impacting such buildings will be influential over longer distances from the point of debris generation in comparison with strong structural materials such as RC and Steel. We can also observe that the variations in model accuracy across the different radiuses considered for debris impact are relatively small: a maximum of 1.03 % (± 2 buildings) for RC, 1.29 % (± 1 building) for Steel, 0.82 % (± 44 buildings) for Wood and 0.80 % (± 10 buildings) for Masonry. This means that between 10 m and 150 m only from a washed away house, the change in the debris impact variable (i.e., the consideration of buildings impacted further from the debris generation point) does not yield large differences in model performance. This possibly indicates that the effects of debris impact should be considered on a much larger scale and/or that the debris impact variable should be refined (for example, by using visual evidence of impact for individual buildings, as done by Reese et al. (2011) in the case of the 2009 Samoa tsunami). Because such evidence is not available, for derivation of the final fragility functions in this study we will use the debris impact radius resulting in the highest predictive accuracy, as shown in Table 4.

Fragility functions

The multivariate fragility functions—Eq. (4)—corresponding to the highest damage state (DS5, defined in this study as the aggregation of damage states 5 and 6 defined by the MLIT, see Table 1) are represented for each building class in Figs. 7, 8, 9 and 10 by fragility surfaces. The range of observed explanatory variable values for the expected probabilities (circles) plotted on Figs. 7, 8, 9 and 10 correspond to the values of maximum flow depths and velocities from the observed data, illustrating the extent of available data coverage. The smooth surfaces are constructed not through spatial interpolation, but by approximating the discrete expected probabilities on a two-dimensional grid (D’Errico 2010). Because the debris impact has been defined as a binary variable, it is possible to represent separately the probability outcomes with and without debris impact.

Fig. 7

Fragility surfaces showing the probability of collapse (i.e., DS5) for Wood buildings, depending on the occurrence of debris impact (radius: 130 m). The expected probabilities are displayed, which color and circle size vary to represent the number of stories (red 1 story, orange 2 stories, cyan 3 stories, black 5 stories or more. There are no buildings in the Wood database with 4 stories)

Fig. 8

Fragility surfaces showing the probability of collapse (i.e., DS5) for Masonry buildings, depending on the occurrence of debris impact (radius: 120 m). The expected probabilities are displayed, which color and circle size vary to represent the number of stories (red 1 story, orange 2 stories, cyan 3 stories, green 4 stories, black 5 stories or more)

Fig. 9

Fragility surfaces showing the probability of collapse (i.e., DS5) for RC buildings, depending on the occurrence of debris impact (radius: 90 m). The expected probabilities are displayed, which color and circle size vary to represent the number of stories (red: 1 story, orange: 2 stories, cyan: 3 stories, green: 4 stories, black: 5 stories or more)

Fig. 10

Fragility surfaces showing the probability of collapse (i.e., DS5) for Steel buildings, depending on the occurrence of debris impact (radius: 30 m). The expected probabilities are displayed; however, due to the lack of information on the number of stories for Steel buildings, no graphical distinction could be made (all circles represent “unknown” number of stories)

The results presented for Wood buildings (Fig. 7) show very clearly that buildings which have been impacted will rapidly reach high probabilities of collapse (i.e., >0.9), from flow depths and velocities as low as 2.5 m and 5.4 m/s, respectively. On the other hand, buildings which have not been impacted will experience a milder increase in collapse probability with flow depth and particularly velocities, ultimately reaching the higher probability range for a combination of very high depths and velocities.

The evolution of collapse probabilities for Masonry buildings (Fig. 8) behaves similarly to the one of Wood buildings. Again the occurrence of debris impact seems to trigger a much steeper rise in damage probability in comparison with the no impact case. However, compared to Wood buildings, high probabilities of collapse (>90 %) when the structure has been impacted seem to occur after flow depth and velocity have reached higher values (7 m and 9.5 m/s, respectively). According to the present results, buildings which have not been impacted would reach a 90 % collapse probability for a combination for moderately severe flow conditions (a flow depth of 4 m associated with a flow velocity of 6 m/s). This can be explained by the fact that Masonry structures are relatively more resistant than Wood buildings (Leone et al. 2011; Suppasri et al. 2013a, b). In addition, it can be noticed from Fig. 8 that the range of flow depths and velocities available for buildings which have not been impacted is very reduced in comparison with the impact case. A meaningful extrapolation and interpretation of the fragility surface beyond the range of the available data would require additional statistical prediction methods to be discussed and applied; however, it is expected for larger values of tsunami IMs the shape of the fragility surface in the no impact case would resemble the one for Wood buildings.

The fragility surfaces for RC buildings (Fig. 9) also show an important increase in collapse probability in the case of debris impact, with very rare occurrences of collapse when the building is not impacted. Similarly to the dataset for Masonry buildings, the range of flow depths and velocities in the no impact case is much smaller than in the impact case, with most expected probabilities of collapse being very small (i.e., <0.15). The shape of the corresponding fragility surface for larger values of these IMs is thus difficult to infer. In line with previous studies (Rossetto et al. 2007; Mas et al. 2012; Suppasri et al. 2013a, b), the much steeper fragility surfaces for Wood and Masonry structures show that RC buildings are more resistant to tsunami loads. An interesting feature of the fragility surface corresponding to impacted buildings is the visibly stronger influence of flow velocity on the rate of increase in damage probability, compared to flow depth. This could be expected as the dynamic impact force is proportional to the square of the flow velocity, although such relativity between the effects of the two variables seems less prominent in the case of weaker structural types. This indicates that hydrostatic loads alone may not significantly determine RC building collapse, and is consistent with previous findings demonstrating flow depth alone to be a poor predictor of tsunami damage for RC structures (Charvet et al. 2014b).

In the case of Steel buildings (Fig. 10), the difference between the impact and no impact cases is less striking than for other building types. The rate of increase in collapse probability appears similar in both cases, with regard to flow velocity. The increase in damage probability with flow depth appears very minor for buildings which have not suffered debris impact, and in line with the result from Charvet et al. (2014b) for Steel buildings this also indicates the hydrostatic loads may not have a significant influence on damage for this construction material. Nevertheless, it can be seen that the scarcity of data for this construction type leads to results which are inconsistent with the other building classes.

The construction of the fragility surface for the non-impacted buildings in the high probability region is mainly driven by one high probability point, with most of the data lying in a range of very low probabilities (i.e., <0.10). Similarly, the collapse probabilities for impacted buildings are mostly <0.50, so half of the probability domain cannot be reliably covered by the fragility function. Thus, the probability values shown by the fragility surfaces for Steel buildings should be considered of limited use, until such functions can be refined using additional data. Information on building height is also crucial to update model estimations consistently with the other construction classes considered.

Given the nature of the new fragility functions estimated in this study, which are multivariate, derived using different statistical assumptions, methods, and model diagnostics compared to previously published research, the fragility results cannot be directly and qualitatively compared. Nevertheless, and regardless of the statistical estimation methodology adopted, all previous studies without exception derived two-dimensional fragility functions (i.e., fragility curves), mostly relating the maximum tsunami flow depth to damage probabilities. Therefore, as a point of reference fragility curves are also derived here, based on the measured flow depth only as explanatory variable (Fig. 11), and consistently with the ordinal regression method adopted throughout the paper. Table 5 shows example combinations of maximum flow depths and velocities yielding specific collapse probability thresholds (i.e., 0.25, 0.50, 0.75, 0.95) from the fragility results presented in this section (Figs. 7, 8, 9, 10, 11). This allows for the comparison of outcomes between the multivariate fragility functions (in cases of both impact and no impact), and simple fragility curves. The examples values chosen indicate fragility curves based on flow depth only may underestimate collapse probabilities, particularly in cases where debris impact has a dominant effect.

Fig. 11

Two-dimensional fragility functions derived using ordinal regression, and flow depth as the only explanatory variable

Table 5 Combinations of flow depth and velocity values for corresponding collapse probabilities, using fragility surfaces (impact/no impact) and fragility curves (one explanatory variable only)

Conclusions

The most commonly used tsunami intensity measure in the derivation of fragility functions is the flow depth measured from post-tsunami surveys; in a few cases the tsunami velocity, retrieved from numerical simulations. To date, fragility functions have all been empirical (based on field damage data) and typically derived using linear least squares regression, assuming a normal or lognormal distribution of the response (i.e., damage state). Latest research has found this method to have serious limitations and be in principle inadequate in the estimation of tsunami-induced damage probability. Therefore, improved statistical modeling techniques, based on generalized linear models, have been recently proposed and applied to case studies of building damage caused by the 2011 Great East Japan tsunami. The uncertainty still visible from recent model estimations was attributed to a lack of explanatory variables, as flow depth alone may not be able to explain the full extent of observed building damage. Indeed, flow velocity, debris impact and scour concurrently act on the affected structure during a tsunami attack.

Therefore, the focus of the present analysis was the application of generalized linear models (more specifically ordinal regression) to building damage data from the 2011 Great East Japan tsunami event, simultaneously taking into account the maximum tsunami flow depth, velocity, and debris impact as explanatory variables. Ordinal regression is a specific case of GLM application where the response variable (i.e., damage state) is assumed to be discrete and ordered, which was deemed suitable to represent the damage classification. Kesennuma city in Japan was one of the most severely affected cities during the event, and a large disaggregated database of building damage and measured flow depths was provided by the city thus making this area the chosen case study. Tsunami inundation simulations were carried out using nonlinear shallow water equations and a nested grid system. The maximum numerical flow velocities were retrieved from the simulation results. The debris impact variable was defined as a binary indicator, determined by the vicinity of the target building to a structure which had been washed away (i.e., assuming the remains of this structure would impact the surrounding buildings). As such, the debris impact variable was assigned a value of ‘1’ if the target building was considered impacted by debris, i.e., close to at least one washed away structure, ‘0’ otherwise. Because the distance of significant debris impact is unknown, a range of debris action radiuses (10 m–150 m) was considered.

The first stage of the analysis consisted in selecting the model components through an assessment of the relative goodness-of-fit between several candidate models. Firstly, the assumption that an ordered model was preferable to a multinomial model was verified using a likelihood ratio test. The same procedure allowed for checking the significance of all explanatory variables and interactions to be added to the simplest model, based on maximum flow depth only. The additional variables considered were maximum flow velocity, debris impact, building material, and number of stories. The AIC was used to choose the most appropriate link function. The final GLM was chosen to be ordered, with a logit link function, and including flow depth, flow velocity, debris impact, building material, number of stories and most associated interactions as explanatory variables. In order to quantify the absolute goodness-of-fit, a penalized accuracy measure was proposed. This measure is considered a more suitable alternative for ordinal models compared to the traditional accuracy (or classification error rate), better suited to binary classifications.

The second stage of the analysis consisted in using this measure, estimated through a repeated tenfold cross-validation scheme, to assess the predictive accuracy (i.e., performance of the proposed model with unseen data) for each building material and each debris impact radius. It was found the model chosen was able to predict the observed damage states in Kesennuma with high accuracy (>90 %) for all building classes. It is possible, however, that these values of accuracy also partly reflect the extreme commonality of high damage states in the database, and alternative measures of goodness-of-fit, such as meaningful correlation measures between observed and expected probabilities (Zheng and Agresti 2000) may need to be developed to complete our understanding of model performance.

The final stage of the analysis focused on the representation of the building fragility results in Kesennuma in the form of fragility surfaces for each building material. Each surface showed the change in building collapse probability with simultaneous changes in maximum flow depth and velocity, considering also the number of stories of the structure. The fragility trends were found to be consistent with previous studies, with Wood buildings found to be the least resilient to tsunami loads, followed by Masonry buildings, RC and Steel buildings found to be the strongest structural types. For RC and particularly for Steel buildings in the no impact case, it was also found that the change in damage probability was only weakly explained by flow depth, confirming previous findings on the poor performance of flow depth alone as a predictor of tsunami damage for these structures. The results obtained with multidimensional fragility functions were compared with classic two-dimensional fragility curves for the city of Kesennuma, and the results indicate that fragility curves, based on flow depth only, may significantly underestimate building collapse probabilities. Except for the case of Steel buildings, for which additional data would be desirable to obtain reliable fragility results, fragility surfaces for all structural materials show the influence of debris impact to be paramount in the determination of high collapse probabilities. In order to provide high-quality fragility assessment tools, interpretable and usable for the tsunami risk assessment community, future studies on tsunami-induced damage probability should aim to:

• Refine the debris impact variables to be used for fragility assessment (for example by considering variability in debris size, mass, sheltering, azimuth of impact),

• Improve numerical velocity calculations by using more sophisticated fluid dynamics models, dynamically varying friction conditions, and detailed topography information,

• Investigate the effects of combined, time-dependent flow depths and velocity to capture more accurately the demand imposed by hydrodynamic loads,

• Quantify the effects of scour on high structural damage probabilities,

• Provide meaningful representations of multivariate fragility functions. Address uncertainties in parameter estimation (measurement error in the variables) by using Bayesian estimation techniques as alternatives to maximum likelihood.