1 Introduction

The Chilean coast has been hit by several far- and near-field tsunamis. One of the last destructive near-field tsunamis was caused by the 2010, M w 8.8, Maule, Chile megathrust earthquake and devastated the Chilean shore (e.g., Lay et al. 2010; Vigny et al. 2011). The impact at far field of a tsunamigenic earthquake is rather well understood in terms of its effects at transoceanic distances. For instance, the arrival time of the leading wave of a tsunami can be computed in advance, thus providing enough warning time for the population and authorities to mitigate disaster and human losses, and then, in most of the cases, the evacuation plans can work.

However, the effect of near-field tsunamis is still not well understood. Several factors control their generation, propagation and effect onshore, such as inundation and runup, and these topics are currently being investigated (e.g., Yamazaki and Cheung 2011; Yamazaki et al. 2011b; Lay et al. 2011). The destructive tsunami generated by the 2011, M w 9.0, Tohoku-Oki, Japan, megathrust earthquake, that occurred along the Japanese subduction zone, has evidenced the need for a better understanding of the tsunami generation process (Ide et al. 2011) and, in particular, its relationship with seismogenic subduction zones (Fujii et al. 2011).

To model near-field tsunamis, it is important to have not only good quality input data, such as a high-resolution bathymetry/topography for tsunami propagation and inundation purposes, but also a complete description of the earthquake source parameters, including fault geometry, seismic moment, focal mechanism and co-seismic slip distribution. Recent studies show that a detailed description of the rupture process considering a realistic fault geometry, and/or space–time slip distribution, improves the computed near-field tsunami (e.g., Ide et al. 2011; Fujii et al. 2011), because these earthquake source effects control part of the strength of the tsunami. For instance, Poisson et al. (2011) analyzing some co-seismic slip models of the Sumatra 2004, M w 9.1, event, concluded that a complex description of the source model is absolutely necessary for tsunami modeling, but also some physical parameters, such as rupture kinematics, should be taken into account for this event and for long faults.

Northern Chile has been recognized by several authors as a seismic gap, and therefore, it is a subducting continental margin highly exposed to the occurrence of a tsunamigenic megathrust earthquake (e.g., Nishenko 1985; Comte and Pardo 1991). The last one occurred on May 10, 1877 (Milne 1880), with a moment magnitude estimated at M w 8.9 (Kausel 1986). The same region was hit just nine years before by the 1868, M w 8.8, megathrust earthquake and tsunami that occurred in southern Peru (e.g., Comte and Pardo 1991). On April 1, 2014, a large thrust event broke a small zone of the megathrust in the northern Chile seismic gap and was followed by a moderate tsunami. This M w 8.1 earthquake, with epicenter near the Pisagua town, broke the middle segment of the megathrust, spanning approximately from 30 to 55 km depth, reaching a rupture length of about 180 km. The estimated magnitude by several groups was about M w 8.1–8.2 (e.g., Hayes et al. 2014; Ruiz et al. 2014; Schurr et al. 2014; Lay et al. 2014; An et al. 2014). The northern and southern segments of the Pisagua rupture zone are still unbroken, and the question about how the northern Chile seismic gap will break in the future still remains.

Improving tsunami hazard studies in the near field needs to address earthquake source size for the largest expected seismic event and to have a good description of the source parameters that control the displacement of the seafloor during the earthquake. The modeling of realistic 3D seafloor displacements due to the rupture process of an earthquake is a key element to be addressed in tsunami simulations for future large earthquakes. However, because the rupture duration of large earthquakes is usually shorter than the long period involved in tsunami wave propagation, the total rupture time history can be neglected for some events and studies.

Earthquake ruptures are complex processes, and the slip imaged of past earthquakes presents spatial heterogeneities at various scales and at different earthquake sizes (e.g., Mai and Beroza 2002). Even for a same event, the co-seismic slip of the 2010, M w 8.8, Maule earthquake, imaged using different inverse methodologies and dataset presents also strong spatial variability (e.g., Lay et al. 2010; Vigny et al. 2011). The resulting variability in these slip models can be interpreted as epistemic uncertainty due to modeling errors when using different dataset and methods. Similar observations can be pointed out for the 2011, M w 9.0, Tohoku-Oki earthquake (e.g., Simons et al. 2011; Yagi and Fukahata 2011; Lay et al. 2011; Yoshida et al. 2011), where the peak-slip amplitude retrieved lies in the order of 40–50 m. Under this perspective, uniform slip over an extended seismic source is an oversimplification for modeling hypothetical future earthquakes. The use of spatial heterogeneous slip models to characterize earthquake source complexity is a better approximation to model a more physical seismic source.

Several earthquake models have been proposed to describe the seismic source complexity (e.g., Andrews 1980; Herrero and Bernard 1994; Mai and Beroza 2002; Gallovič and Brokešová 2004; Ruiz et al. 2007). In particular, Andrews (1980) proposed a stochastic source model to generate spatially heterogeneous slips. Inspired by this work, Herrero and Bernard (1994) developed a kinematic earthquake source model by generating k −2 slip distributions, where k is the radial wavenumber.

We expect that uniform versus heterogeneous slip distributions for a certain large tsunamigenic earthquake will produce a different static displacement field in the medium, and then, as a consequence, one could expect large differences in terms of the effects of the near-field tsunami and the runup height along the shore (e.g., Geist and Dmowska 1999).

The aim of this work is to present a case study and to statistically assess the variability in the runup distribution caused by homogeneous and heterogeneous slip models of earthquakes, by modeling the tsunami in the near-shore domain. The target zone is the northern Chile seismic gap, whereas an hypothesis we assume as a worst case scenario the occurrence of a M w 9.0 megathrust earthquake. The fault would break the whole segment going northward from the Mejillones Peninsula (~32.3°S) to the city of Arica, as suggested by some authors (e.g., Abe 1979; Kausel 1986; Comte and Pardo 1991; Kausel and Campos 1992). We model heterogeneous k −2 slips distributed over a non-planar complex rupture fault which approximates the seismogenic plate interface in northern Chile. Several stochastic slip distributions are generated, and the vertical static displacement is then computed. The passive tsunami generation approach is used for each slip, and a statistical analysis of the runup distribution generated along the coastal border is done.

2 Earthquake rupture for a M w 9.0 in northern Chile

2.1 Historical large earthquakes in the northern Chile seismic gap

Northern Chile and southern Peru belong to a convergent margin, related to the subduction of the Nazca plate underneath the South American plate, characterized by a convergence rate at the trench estimated at about 6.5–7.0 cm/year (e.g., Norabuena et al. 1999; Sella et al. 2002). Northern Chile, our study area—covering basically from the city of Arica to Antofagasta (between the latitudes 18.5°S and 23.5°S)—has been struck by several large earthquakes. The last megathrust earthquake was the 1877, M w 8.9, that caused a destructive tsunami. Historical reports also indicate that this zone has been shook by two large earthquakes in 1543 and 1768 (Comte and Pardo 1991; Vargas et al. 2005). These authors suggest that both events have broken apparently the same rupture area than the 1877 event (Fig. 1).

Fig. 1
figure 1

Northern Chile and southern Peru map showing the estimated rupture length and year of occurrence of historically reported and instrumentally recorded, large and megathrust earthquakes

Full size image

Vargas et al. (2005) using high-resolution sedimentological and geochronological techniques, of a Holocene sedimentary sequence in the Mejillones Bay (~23°S), infers the occurrence of two past great subduction earthquakes. The first one dated between the years 1409 and 1449, with an associated tsunami, but unfortunately no written reports exist to measure more precisely the rupture area. The second large seismic event, dated between the years 1754 and 1789, may coincide with the 1768 historically documented earthquake analyzed by Comte and Pardo (1991).

The 1995, M w 8.1, Antofagasta thrust earthquake occurred at the southern edge of the northern Chile seismic gap region (e.g., Delouis et al. 1997; Ruegg et al. 1996). On November 14, 2007, a M w 7.7 earthquake hit the city of Tocopilla and surrounding areas. The studies conducted on this earthquake suggest that the rupture broke the deeper zone of the seismogenic contact interface and stopped northward approximately at the latitude of the Mejillones Peninsula (Delouis et al. 2009; Loveless et al. 2010; Peyrat et al. 2010) and then just filling a small area of the expected seismic gap. The Mejillones Peninsula is a geomorphological feature that some authors have suggested that may act as a barrier stopping the rupture propagation of large earthquakes (Victor et al. 2011; Béjar-Pizarro et al. 2010). On the other hand, the 2001, M w 8.4, Arequipa thrust earthquake broke the southern Peru subduction margin, and from the spatial distribution of aftershocks, the rupture was inferred to stop at the latitude of Ilo City (Tavera et al. 2002). It means there is still an unbroken portion between the cities of Ilo and Arica, since the last 1868, M w ~ 8.8, Peru megathrust earthquake ruptured the southern Peru down to Arica (Dorbath et al. 1990).

Focusing on the last historically reported megathrust earthquake that struck the northern Chile seismic gap in May 9, 1877, the moment magnitudes estimated by some authors are M w 8.9 (Kausel 1986) and M w 8.8 (Comte and Pardo 1991). Additional magnitudes assigned are Ms 8.5 (Lomnitz 2004) and M t 9.0 (Abe 1979). This very large event generated a destructive tsunami with waves of 3 m height reported at Pisco town and propagated throughout the Pacific. Despite the scatter on the magnitude estimates, if one considers a total fault length of about 550 km (from 18°S to 23°S), one could expect at least a M w 9.0 breaking the whole segment.

Interseismic coupling studies conducted in the northern Chile seismic gap suggest a high seismic coupling zone along the seismogenic contact interface (e.g., Chlieh et al. 2011; Béjar-Pizarro et al. 2013; Métois et al. 2013). However, the coupling maps proposed by these authors also show a large spatial variability; for instance, Métois et al. (2013) propose a low coupling zone at the latitude of Iquique (~20.5°S), and Chlieh et al. (2011) instead propose a fully coupled zone from Antofagasta to Arica.

On April 1, 2014, a large thrust event hit northern Chile and broke a small zone of the megathrust. It was followed by a moderate tsunami. This M w 8.1 earthquake ruptured approximately the middle segment of the megathrust along the northern Chile seismic gap. The co-seismic slip took place mainly from 30 to 55 km depth, over a rupture length of ~180 km, and the magnitude computed by several groups was about M w 8.1–8.2 (e.g., Hayes et al. 2014; Ruiz et al. 2014; Schurr et al. 2014; Lay et al. 2014; An et al. 2014). Some co-seismic slip models agree that the slipped zone occurred mainly in the deeper part of the megathrust (e.g., Hayes et al. 2014), so the rupture did not break upwards near the trench. The northern and southern segments are still unbroken; thus, there still is a large area that could break, as a worst case scenario, following a M w > 8.5 (Schurr et al. 2014) earthquake with its potential tsunami. These unbroken segments raise the question about how the northern Chile seismic gap will break in the future.

Considering this background, the 2014, M w 8.1, Pisagua earthquake was not entirely unexpected, but this earthquake occurred with a slip deficit from its maximum potential. The upper portion of the broken segment, the northern segment and southern segments of the original seismic gap are still unbroken, leading us to think that the possibility of a megathrust earthquake still remains (e.g., Hayes et al. 2014).

2.2 Setting a non-planar complex rupture fault geometry

Interpreting the abrupt strike change of the trench axis and coastline at the latitude in Arica City, as well as the Mejillones Peninsula, as geometrical and geomorphological features that may act like a barrier to stop the rupture propagation, one can assume a fault zone extending from Mejillones to Arica. Because the seismogenic plate interface presents a complex geometry along strike and downdip in this region, we construct a non-planar fault to define the earthquake rupture.

To define the non-planar rupture surface, we located the origin coordinate at 71.34°W and 23.20°S, which correspond to the southwest vertex of the fault, at about the latitude of the Mejillones Peninsula. The top fault was buried at 8 km depth at the trench axis. It means the rupture does not break the free surface, and a buried rupture is assumed. The computation of the elastic deformation in such a complex mechanical and rheological environments is difficult to handle. We define seven segments along strike going northward with partial length of 200, 55, 55, 50, 50, 45 and 45 km and strike angles 3°, −3°, −6°, −11°, −20.5°, −31° and −41.5°, respectively. These values were set so the upper edge of the fault spans the trench axis, covering a total length of 500 km along the top fault. The rupture surface downdip was defined with six segments having 30 km of partial width each one and dip angles of, 10°, 12°, 15°, 19°, 22° and 24°. The approximate downdip geometry was determined from USGS Slab 1.0 model (Hayes et al. 2012) between the latitudes 23°S and 21.5°S. The total fault width is 180 km, and the deepest fault zone reaches 58 km depth approximately. The geometry along downdip—orthogonal to the trench axis—was preserved all along the strike direction. This allowed us to define local coordinates along strike and dip and, therefore, to mesh the fault surface easily, defining N x and N y subfaults along strike and dip, respectively. An example of the structured mesh composed by planar quadrilateral elements is shown in Fig. 2a.

Fig. 2
figure 2

Rupture fault geometry setting. a 30 arc-s bathymetry in northern Chile and the non-planar mesh that defines the rupture for a M w 9.0 megathrust earthquake breaking the northern Chile seismic gap. Four cross sections orthogonal to the trench axis are shown, b A–A′, c C–C′, d B–B′, e D–D′. In each profile, the downdip fault geometry (black line) is compared against USGS Slab 1.0 (gray line) (Hayes et al. 2012)

Full size image

The total length computed along the local coordinate of the deeper edge of the fault following the strike was 660 km, and the total fault area is about 1.022 × 105 km2. The non-planar complex fault geometry is compared against the Slab 1.0 model (Hayes et al. 2012) at four cross sections (Fig. 2b–d, f). Just minor differences are observed at the two northern profiles and deeper fault zones of the assumed fault surface.

The lower boundary of the seismically coupled interface is located at 40–50 km, as deduced from background seismicity (e.g., Tichelaar and Ruff 1993; Comte et al. 1994; Comte and Suarez 1995; Delouis et al. 1996) and from geodetic measurements of interseismic strain (50 km depth after Bevis et al. 2001; 55 km depth after Khazaradze and Klotz 2003; 35 km depth and a partially coupled zone between 35 and 55 km after Chlieh et al. 2004).

2.3 Stochastic complex earthquake rupture model

The earthquake rupture is a complex process, which from a kinematic modeling point of view requires a complete and detailed description of the spatial and temporal history of the slip. For instance, the co-seismic slip of earthquakes imaged using kinematic inversion, and different kinds of seismological datasets present a strong spatial–temporal variability at different scales (e.g., Mai and Beroza 2002).

For local tsunami, the spatially heterogeneous static co-seismic slip on the fault controls tsunami wave amplitudes (Geist and Dmowska 1999; Geist 2002). Motivated by these works, our study describes static heterogeneous slip distributions using a stochastic k −2 earthquake source model for near-shore tsunami modeling.

Andrews (1980) showed that if the slip spectrum amplitudes falloff as k −2 in the wavenumber domain, then, the source radiates a far-field displacement spectrum that follows the classical ω −2 model proposed by Aki (1967). The so-called k −2 self-similar source model was introduced by Herrero and Bernard (1994) inspired by Andrews’ (1980) work, in which the slip spectrum is imposed to decay proportionally to k −2 beyond a corner wavenumber, \({k_{\text{c}} }\), which is defined as \({k_{\text{c}} = 2\pi /L_{\text{c}} }\). The L c length is related to some characteristic fault scale, usually the fault width or length. The assumption in both source models is that the stress drop, Δσ, of earthquakes is scale invariant.

The slip distribution is randomly generated by computing a 2D stochastic spatial random field and imposing in the wavenumber domain a k −2 spectral decay of the 2D Fourier amplitude of the slip at high radial wavenumbers (e.g., Andrews 1980; Herrero and Bernard 1994). Several methodologies have been proposed to generate spatial random k −2 slip distributions and have been used to model complexity of earthquake ruptures (e.g., Herrero and Bernard 1994; Bernard et al. 1996; Mai and Beroza 2002; Gallovič and Brokešová 2004; Ruiz et al. 2007).

The 2D Fourier slip spectrum can be written as being proportional to,

$${\Delta \tilde{u}(k) \propto \frac{1}{{1 + \left( {\frac{k}{{k_{\text{c}} }}} \right)^{2} }}e^{i\varphi \left( k \right)} }$$
(1)

where \(\varphi(k)\) is the spectral phase, \({k = \sqrt {k_{x}^{2} + k_{y}^{2} } }\) is the radial wavenumber, and \({k_{x} }\) and \({k_{y} }\) are the wavenumber components along the \(x\) and \(y\) directions, respectively. Random phases are introduced when \({k > k_{\text{c}} }\) to generate heterogeneous spatial slip at high wavenumber, while at shorter \(k\) values a coherent phase distribution is imposed. The numerical computation is performed in the wavenumber domain, using a discrete 2D fast Fourier transform (FFT). After imposing the spectral behavior, an inverse 2D FFT is applied to compute the slip in the spatial domain \({\Delta u\left( {x,y} \right)}\). The slip is tapered to avoid nonzero slip amplitude at the edges of the fault, which may induce high stress concentrations, and finally, the slip is normalized to the target seismic moment.

Figure 3 shows a numerical realization of a stochastic k −2 slip distribution for a M w 9.0 earthquake. Because the rupture surface in northern Chile has a complex geometry, we estimate the average fault length as L avg = A tot/W, and this gives L avg = 568 km, where A tot is the total fault surface. The fault was subdivided in a regular grid mesh of N x  × N y  = 256 × 64 subfaults. The slip is spatially heterogeneous (Fig. 3a), and the amplitude of the 2D Fourier spectrum of the slip fall offs as k −2 at high wavenumbers (Fig. 3b). It is worth noting that the spectral decay of the 2D Fourier spectrum of slip distributions imaged for several past earthquakes is to first-order in agreement with a k −2 spectral decay (e.g., Somerville et al. 1999; Mai and Beroza 2002). Also, the fault size and magnitude also follow standard empirical scaling relationships for large earthquakes occurred along the seismogenic interface (e.g., Strasser et al. 2010; Blaser et al. 2010).

Fig. 3
figure 3

Numerical realization of a stochastic k −2 slip distribution for a M w 9.0 earthquake. a Spatial distribution and b amplitude of the 2D Fourier spectrum of the slip as function of the radial wavenumber k

Full size image

2.4 Modeling co-seismic static displacement field for complex slip earthquake

We compute the 3D static displacement field at the free surface using the Okada’s (1992) formulas that allow to compute internal static displacements and strains due to shear and tensile faults buried in a homogeneous elastic half-space for both, point source and finite rectangular faults.

2.4.1 Static displacement field from uniform dislocations

In this work, the co-seismic displacement field is calculated for a heterogeneous k −2 slip. The finite fault is discretized into subfaults to generate heterogeneous slips and to take into account the spatial variability of the slip at several scales. The total displacement field at the free surface is given by the sum of displacements from each subfault, which follows basically the discrete version of the representation theorem of seismic sources (Aki and Richards 1980). A similar approach is usually used in some tsunami modeling and source studies (e.g., Satake and Kanamori 1991; Geist 2002). At each subfault, the expression of a point-source elastic shear dislocation is used (Okada 1992); it means that for shear dislocations—or double-couple point sources—the moment size needs to be specified, basically \({\mu \cdot \Delta \bar{u} \cdot \Delta \varSigma }\), where \(\mu\), \(\Delta \bar{u}\) and ΔΣ are the rigidity, average slip and area of the subfault, respectively. The rigidity used was 45 GPa (Husen et al. 1999).

In order to test the accuracy of using a meshed fault plane to compute the static displacement field, we compared the numerical solution computed from a rectangular finite fault with uniform dislocation (Okada 1985) and the one obtained using a discrete approach. Geist (2002) suggests that a subfault size (Δx) less than or equal to the point-source depth can adequately represent the seafloor displacement field used to model tsunami propagation. For a M w 9.0 earthquake, the subfault grid size was set as Δx = L avg/N x  = 2.2 km and Δy = W/N y  = 2.8 km. The top fault was buried at 8 km depth, and the earthquake follows an inverse fault mechanism. The fault geometry was fixed to ϕ s = 0°, δ = 18° and λ = 90°, corresponding to strike, dip and rake, respectively. Figure 4 shows the vertical and horizontal static displacement components computed at the free surface using the discrete approach. We computed the norm two errors for the horizontal and vertical components, and the maximum values are in the order of 2 and 1 %, respectively. The largest differences retrieved are located in a thin strip along the strike for points located the nearest to the upper edge of the fault. In this test, a uniform slip is assumed and no taper is applied. So, the non-smooth slip at the fault edges generates non-realistic stress concentrations and may produce stress singularities in the vicinity of the fault. To avoid this, a taper is applied to smooth the slip at the fault edges.

Fig. 4
figure 4

Static co-seismic 3D displacement field computed at the free surface using a point-source discrete approach to model an extended source defined by a rectangular planar fault having an uniform slip dislocation (fault dimension, L avg × W = 567 × 180 km2, and uniform slip, D = 7.8 m). The map view shows in color the vertical displacement and the vectors correspond to the horizontal displacement

Full size image

2.4.2 Static displacement from uniform versus heterogeneous k −2 slip distribution for a M w 9.0 earthquake

To better simulate the seafloor vertical displacement, we introduce heterogeneous k −2 slip to model an hypothetical M w 9.0 earthquake breaking the whole northern Chile seismic gap. For this application, we use the complex non-planar fault geometry built in previous sections (see Fig. 2), and we compare the vertical static displacements computed from two slip distributions. Because the fault mesh generated is regular, we set up N x and N y subfaults along strike and dip, respectively, and one can easily map a heterogeneous k −2 slip, Δu(i, j), generated over a rectangular planar fault to the regular mesh of a non-planar fault geometry. Once the slip is mapped, the static displacement field is computed easily following the discrete point-source approach for an extended seismic source.

The first case corresponds to define a uniform slip tapered at the edges (Fig. 5a), and the second one is a spatially heterogeneous k −2 slip distribution (Fig. 5c). The taper has a width of 20 km at the top and bottom edges and 30 km at the fault ends along strike, and it was applied to both uniform and stochastic k −2 slip distributions. The stochastic slip (Fig. 5c) is spatially heterogeneous at several wavelengths, and large patches of slip are visible at different locations on the fault. The peak-slip reached in this realization is about 40 m, which is of the same order of the maximum slip imaged for the 2011, M w 9.0 Tohoku-Oki, Japan earthquake (e.g., Simons et al. 2011; Yagi and Fukahata 2011; Lay et al. 2011). The respective vertical static displacements computed for each case are shown in Fig. 5b, d for uniform and stochastic k −2 slip, respectively. The vertical displacement from the uniform tapered slip (Fig. 5b) follows a similar spatial pattern to the one shown in the case of a uniform slip on a single rectangular planar fault, which produces uplift near trench and subsidence along the deeper zone of the fault. But in this case, this pattern follows the curvature along strike (Fig. 5b). The maximum uplift is in the order of 3 m. Instead, the stochastic k −2 slip (Fig. 5d) produces a more heterogeneous spatial pattern on the vertical displacement component. One can see two zones having large uplift characterized by peak-vertical displacements of 6.0 m and 8.0 m, located to the south and north of the rupture area, respectively. Let’s point out that this particular pattern corresponds to this particular heterogeneous k −2 slip, we verified that uplift/subsidence distribution changes when a different stochastic slip is used, and largest peak-uplift is reached when large slip patches approach the trench. The peak-vertical displacement from heterogeneous k −2 slip distribution is at least twice as large as the maximum uplift from a uniform tapered slip. In both cases, the largest subsidence is mainly located on the continent, whereas the largest uplift zones occur seawards.

Fig. 5
figure 5

Examples of the vertical static displacement modeled for a M w 9.0 megathrust earthquake in northern Chile when assuming two slip distributions over a non-planar fault geometry. a Uniform tapered slip and the corresponding, b vertical displacement. c Realization of a stochastic k −2 slip distribution and d the resulting vertical displacement field

Full size image

These numerical results show clearly that the static displacement field changes and presents larger amplitudes in the case of heterogeneous k −2 slip distributions than when assuming a uniform slip. We expect that under the frame of passive generation of tsunami, these larger amplitudes of vertical displacement will generate large and complex runup distribution along the shore. In the following section, a statistical analysis is made in order to assess the scatter in the runup amplitudes when considering several stochastic slip distributions for a M w 9.0 earthquake.

3 Near-field tsunami runup modeling

In the next sections, we present the results from numerical modeling of tsunami for several heterogeneous slip models of a case study for a M w 9.0 earthquake in the northern Chile seismic gap.

3.1 Initial condition for tsunami modeling

In this work, the so-called passive generation of tsunami is used. Under this approach, one neglects the dynamic seabed displacement resulting from the earthquake rupture process. It means that the initial condition for tsunami propagation is obtained by translating the final (static) vertical seafloor deformation field to the water free surface, and the hydrodynamics in space and time are computed. Because the vertical co-seismic displacement is an input for NEOWAVE, the numerical code recomputes the initial bathymetry by adding up the vertical deformation. This assumption is rather acceptable following the hypothesis that the total rupture time for a regular tsunamigenic earthquake is shorter than the period of propagating water waves.

3.1.1 Tsunami numerical model

We use a tsunami numerical model, NEOWAVE (Non‐hydrostatic Evolution of Ocean WAVEs), which solves, by means of a staggered finite difference technique, the depth-integrated nonlinear shallow water wave equations that account for a non-hydrostatic pressure through vertical velocity term to describe weakly dispersive waves and a momentum conservation scheme to handle flow discontinuities, such as bores or hydraulic jumps (Yamazaki et al. 2009, 2011a). A wet–dry moving boundary is implemented for detail inundation/runup modeling along the coast and full wave transmission at the open sea. NEOWAVE is a powerful tool to study near-field tsunami from its generation, propagation and inundation processes (e.g., Yamazaki et al. 2011a, b; Lay et al. 2013), and it has been also applied to understand shelf resonance effects of near-field tsunami (Yamazaki and Cheung 2011).

3.1.2 Model setup

The computational domain covers from 95°W to 69°W and from 35°S to 10°S. The simulation runs for the elapsed time of 6 h using a computational time step of Δt = 1 s. NEOWAVE allows define nested grids to compute tsunami propagation over finer grids. In this work, only one global grid is set, having a grid spacing resolution of 30 arc-s (~900 m), which is rather acceptable for the purposes of this study that focuses on compute runup distribution along the coast at regional scale. The Manning coefficient is set up as 0.025, and the vertical wall condition is used at the shore; it means the runup is computed with this boundary condition at the coastline. The lack of high-resolution bathymetry/topography in the study area does not allow us to compute accurately the inundation landwards. The bathymetry used is the one available online through the GEBCO (General Bathymetric Chart of the Oceans) website http://www.gebco.net/ (Smith and Sandwell 1997; Becker et al. 2009).

3.1.3 Setting scenarios for a set of stochastic k −2 slip

We generated 90 heterogeneous k −2 slip distributions for a hypothetical M w 9.0 earthquake breaking the northern Chilean seismic gap. The number of computations represents a good compromise in terms of computational time and storage, in order to generate a good set of tsunami runup scenarios to do statistical analyses. For each slip, we computed the total vertical static displacement field from an extended source at the main grid. The finite fault geometry follows the non-planar complex fault geometry of the seismogenic plate interface proposed in this study. For the whole set of slips randomly generated, the target magnitude, M w 9.0, and the total rupture area are fixed. Because each slip is randomly generated, the peak-slip varies in the range 11–52 m, with a mean peak-slip of 36 ± 5 m. For each slip, we model the tsunami propagation using NEOWAVE and also we calculate the runup distribution along the coastline.

3.2 Analysis of the results

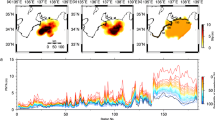
Figure 6 shows the complete set of runup distributions computed in our simulations. We computed the minimum, maximum and mean runup along the shore, and we plotted them as a function of longitude in Fig. 6b. The maximum peak-runup reached is about 35 m. The minimum runup bound fluctuates between 1 and 5 m, for the region shown in Fig. 6a. The mean runup presents roughly a uniform distribution with an amplitude of about 10 m along the coast between 23°S and 18°S, which coincides approximately with the extent of the rupture area. The numerical results also suggest that Mejillones Peninsula, at 23.3°S, may act like a hydrodynamic geometrical barrier that attenuates the runup southward, mainly due to the scattering of waves by the Mejillones Peninsula.

Fig. 6
figure 6

a 30 arc-s bathymetry map for northern Chile. b Comparison of the minimum (red line), maximum (blue line) and mean (black line) runups against the complete set of runup distributions (gray lines) computed in this study

Full size image

We analyzed the runup distribution at a few specific locations along the coastline. Figure 7 shows the histograms computed at latitudes inside and outside of the rupture area. We use the Chi-squared test to compute statistically the probability that the runup distribution comes from a lognormal probability density function. The p value in each panel is the probability of rejecting the null hypothesis, at 95 % of confidence, which in our case is that the runup follows a lognormal distribution. In all histograms, the p value establishes that we cannot reject the null hypothesis. Figure 7 shows, in particular, the location related to the largest peak-runup from the whole set (at longitude −20.73°). It shows similar coefficients of variations assuming Gaussian and lognormal distributions.

Fig. 7
figure 7

Set of histograms of tsunami runup amplitudes computed at different coastline locations of the study area. Average (blue line) and extrema (black line) of the runup distribution for the whole set of tsunami simulations are shown. A lognormal distribution was fitted in each case following a Chi-squared test (see text for details), where c.v. is the empirical coefficient of variation and c.v.LN is the coefficient of variation of the lognormal distribution

Full size image

We also compared our numerical results against empirical laws. Plafker (1997) pointed out that, if there are not abrupt changes in the topography along the coastline, the amplitude of maximum runup is in the order of the maximum co-seismic slip and it cannot be more than twice the co-seismic peak-slip at the source. It is an empirical observation and is known as the “Plafker’s Law.” Rosenau et al. (2010) showed that runup scales linearly with the slip at the source. These rules of thumb are respected here (Fig. 8). If we compare the maximum slip with its maximum runup, we observe that runup scales linearly by a factor between 0.5 and 0.8. Therefore, our numerical results show that the maximum runup is on the order of the maximum co-seismic slip, and then, the simulated peak-runup versus peak-slip confirms Plafker’s rule of thumb with our synthetics scenarios. For the 2010 Maule and 2011 Tohoku megathrust earthquakes, the slip values are 16 m (Hayes 2015, http://earthquake.usgs.gov/earthquakes/eventpage/usp000h7rf#scientific_finitefault) and 55 m (Hayes 2015, http://earthquake.usgs.gov/earthquakes/eventpage/usp000hvnu#scientific_finitefault), and the maximum runup are 29 m (Fritz et al. 2011) and 39.7 m (Mori et al. 2011), respectively (Fig. 8). Our numerical simulations are in agreement with the tsunami-earthquake physics and empirical observations, respecting theses rules of thumb and again proving that the runup is strongly dependent on the slip distribution of the earthquake. This makes essential to include complexity for near-field tsunamis (Geist 2002).

Fig. 8
figure 8

Plafker’s rule of thumb. Simulated near-field peak-runup compared with the maximum co-seismic slip at the source (red dots). Star and diamond correspond to the 2010 Maule and 2011 Tohoku earthquakes, respectively. The straight lines are the ±σ bounds from a linear fitting to the red dots

Full size image

An example of a tsunami runup generated by a heterogeneous k −2 slip distribution is shown in Fig. 9. For this specific realization of slip, the vertical displacement reaches a maximum uplift of about 9 m and a maximum subsidence of 2 m near Iquique (Fig. 9a). The maximum uplift is located near the trench. The numerical runup distribution presents two largest peak-runups in the order of 30 m, reached at 19.5°S and 20.8°S, approximately (Fig. 9b). In the case of a tapered uniform slip, the runup distribution presents smaller amplitudes compared against runup computed from a stochastic k −2 slip. As shown in Fig. 9b, the runup from the uniform slip is just slightly greater than the minimum bound of the runup obtained from the whole set of tsunami scenarios modeled in this study. The stochastic k −2 slip model shown in Fig. 9 presents a large amount of slip in the updip zone of the megathrust, suggesting that large slip located updip near the trench could generate large runup amplitudes along the shore. If we look at past tsunamis, the imaged co-seismic slip models of the 2011, M w 9.0, Tohoku earthquake show that large slip occurred near the trench, and this event caused a destructive tsunami.

Fig. 9
figure 9

a Example of the vertical displacement field computed from a stochastic k −2 slip model and b comparison of the tsunami runup generated by this scenario (black line) against the runup distribution (blue line) from an uniform slip tapered at the edges. The minimum and maximum bounds of the whole set of runup simulated in this study are also shown (gray lines)

Full size image

Following the latter observation, we study the influence of events that concentrate an important amount of co-seismic slip near the trench (in the upper part of the fault plane). We explored every combination of a fraction of the total seismic moment concentrated in a given area in the upper surface rupture to define a statistical threshold to classify the tsunami scenarios. For each pair, we estimate the empirical cumulative density function (CDF). The curves are computed by its definition; that is, P(R max < R, S ∈ RS) is the probability that the maximum runup of the scenario (S) belonging to the family of random scenarios (RS) is lower than a given runup R, where RS can be subset A or B. This allows us to separate our 90 scenarios in two subsets: The subset A contains the events that do not hold the separation criterion, and the rest of the scenarios belong to subset B. Basically, subset B includes slip models that concentrate a given percentage of the total seismic moment near the trench.

The chosen threshold in this criterion should preserve a sufficient number of scenarios in each subset to make statistical analysis. We tested three cases: 40, 50 and 60 % of the total seismic moment concentrated onto the upper half of the fault. Figure 10 shows the comparison of empirical CDF regarding the two subsets, taking the peak-runup as a random variable. As it was said, empirical CDFs are computed by its definition and the confidence bounds are obtained using the Dvoretzky–Kiefer–Wolfowitz inequality (Dvoretzky et al. 1956), which is adapted to estimate the confidence bounds for empirical CDF. For instance, Fig. 10c shows the empirical CDF estimated for subsets A and B, and one can see that slip models with large slip near the trench are more probable to produce higher runup. For example, choosing a runup of 25 m, one can see from the CDF that the empirical probability that the maximum runup of a scenario A is less than 25 m is 0.95; instead, if the scenario is from subset B, it is 0.25.

Fig. 10
figure 10

Empirical cumulative density functions (CDF) for three different cases. The separation criterion pairs (fraction of total seismic moment concentrated in the middle upper part of the megathrust) are a 40, b 50, c 60. Black continuous lines are subsets B (satisfying the separation criterion), and gray continuous lines are subsets A (not satisfying the criterion). The dashed lines are the 95 % confidence bounds computed with the Dvoretzky–Kiefer–Wolfowitz inequality

Full size image

Notice that in the three cases, the CDF of subset B is always less than the CDF of subset A. Thus, we state statistically that events with large amount of slip, located in the upper part of the rupture zone, produce higher peak-runup than the remainder slip models. Despite the fact we over pass local features (for instance, bathymetry or major geomorphological features) when analyzing the runup maxima, the previous statistical computation was developed to retrieve global characteristics of the tsunami hazard, generally associated with the peak-runup.

For comparison purpose, Fig. 11 shows the subset B corresponding to slip models that present at least 60 % of the total seismic moment in the upper half of the megathrust. Their respective empirical CDF is shown in Fig. 10c. From the 90 slip models, 68 fall in subset A, and 22 in the other one. Figure 11 shows the runup distribution for each subset. The runup distribution and the mean along the latitude are shown in Fig. 11a. The mean runup fluctuates in the order of 6 m, from 23°S to 18°S. Instead, for subset B, the mean curve follows the bound around 10 m (Fig. 11b), and it is almost systematically greater than the mean runup curve computed for subset A. This is depicted in Fig. 8c that shows the difference of the runup distribution along latitude of subsets A and B. One can see that the largest differences occur between latitudes 23.1°S, 21.2°S and 18°S, basically where the rupture area is located. For instance, the zone at 23.1°S corresponds to the Mejillones Peninsula and coincides with the southern edge of the rupture. Similarly, the 18°S coincides basically with the northern end of the rupture zone. Instead, the decrease in the mean differences observed at ~21°S from both subsets could be related to the local bathymetric feature, where the width of the continental shelf is wide in comparison with the rest of the study area, and the continental slope is steep. To precise this latter effect, more specific analysis are needed, which are out of the scope of this study.

Fig. 11
figure 11

Results for the runup distribution when considering two subsets of heterogeneous k −2 slip models, A and B, selected from the complete set of slip. Subset A is the so-called near-trench slip models, which corresponds to the ones that concentrate at least 60 % of the total seismic moment in the upper middle part of the non-planar fault, and subset B are the remaining slips. a Runup distributions (gray line) and its mean curve (black line) for subset B, and b all runup distributions (gray line) and its mean curve (black line) for subset A. c Difference of the mean curve of subsets B and A

Full size image

4 Discussion and conclusions

In this work, as a case study, we simulated numerically the tsunami generated by a hypothetical M w 9.0 megathrust earthquake breaking the whole segment in the northern Chile seismic gap. We generated a set of stochastic k −2 slip distributions built-up under the frame of physics-based earthquake source models. The stochastic slip was distributed (mapped) onto a non-planar fault that follows the plate interface from Mejillones Peninsula to southern Peru. Under the framework of passive generation, the tsunami was modeled, and we statistically assessed the runup variability along the shore.

Our simulations show peak-runup that can vary from 10 to 40 m in the case of heterogeneous k −2 slip distributions, and the main region affected by this large variability is basically the rupture area of the assumed hypothetical earthquake from 23°S to 18°–17°S. Instead, the minimum runup along the coast from the whole set of heterogeneous slip models tested almost coincides with the runup computed from the tapered uniform slip model. As pointed out by Geist (2002), in the near field it is very important to consider non-uniform slip distributions, because the runup is then not underestimated as occurs with earthquake sources having uniform slip. Our numerical results support the latter conclusion, but now applied in a more complex fault geometry and for a larger earthquake. As Geist (2002) pointed out, and as our numerical simulations show, the runup of local tsunamis is strongly dependent on the slip distribution of the earthquake, making it essential to take into account the complexity of the source for near-field tsunamis. This effect is observed from numerical simulations using a coarse bathymetry grid (30 arc-s, in this study), which can be even greater with a refined grid and high-resolution bathymetry mapped near the shore. This means that for a better estimate of runup from local tsunami—in the near field—the uniform slip assumption should be avoided.

Also, we checked that our numerical results respect the so-called Plafker’s Law, based on empirical tsunami observations, providing additional arguments that these kinds of methodologies can be used for tsunami hazard studies.

As observed in the case of the tsunami following the 2011, M w 9.0, Tohoku-Oki earthquake, the slip imaged by several groups agrees that a large amount of slip concentrated near the trench. This tsunami devastated the Japan shore, and the maximum runup measured on the field was about ~40 m. Our numerical simulations show that in the case of slip models that present at least 60 % of the total seismic moment concentrated in the middle upper part of the megathrust, the simulated peak-runup can reach values in the order of ~35–40 m. The empirical CDF estimated from the simulations shows that slip models with large slip near the trench are more probable to produce higher runup. This analysis provides a global knowledge expected for the tsunami hazard, by passing local effects. Nonetheless, the ignored local features were studied by performing the corresponding statistics for fixed locations along the coastline. Those cases reveal a characteristic behavior that follows a lognormal distribution with high confidence. Hypothesis tests were done in order to verify statistically the runup probability distribution pattern at different latitudes. The curve trend might be a signature stamp from the intrinsic runup process. However, more test and more scenarios should be run to confirm this claim.

Certainly, our study focuses on numerical simulations of a hypothetical earthquake, and several other factors (not taken into account in this study) may affect the tsunami runup in the near field, which include (1) horizontal displacements of the seabed, (2) high-resolution bathymetry near the shore, (3) the dynamic displacement of the seafloor caused by the space–time rupture process (e.g., Poisson et al. 2011). On the other hand, a better resolution of detailed bathymetric charts in the study zone may improve our analysis to regional scale and the computation of runup distributions.