1 Introduction

Spatial seismicity patterns are usually proved to correlate well with the respective patterns of static Coulomb stress changes (ΔCFF or ΔCFS), since more aftershocks commonly occur in the positive rather than in the negative ΔCFF lobes (Harris 1998 and references therein). Changes in seismicity rates are therefore likely to be related to changes in stress, as evidenced by aftershock activity or by more subtle seismicity dynamics caused by nucleation processes of large earthquakes. Other phenomena that may induce changes in earthquake production rates are dynamic stress changes caused by the propagation of seismic waves, pore fluid diffusion, magma intrusion in active volcanic areas, viscoelastic relaxation, postseismic slip and creeping. Quantitative measures of a change in seismicity are also required, especially when trying to detect specific patterns (e.g., relative quiescence) prior to large shocks, as an attempt to identify precursory phenomena that could be used for earthquake prediction strategies (Marsan and Wyss 2010).

Dieterich (1994) introduced the rate/state-dependent friction formulation in order to associate shear stress changes with seismicity rate variation. Later, this perspective was modified by introducing the more complex static Coulomb stress failure along with the rate/state model. Following this concept, positive Coulomb stress changes amplify the background seismicity, and therefore, small stress changes produce large changes in seismicity rate in areas of high background activity (Toda et al. 2005). Similarly, seismicity rate depressions in the stress shadows are evident only in areas with high seismicity rates immediately beforehand (Harris and Simpson 1998; Stein 1999). Mallman and Parsons (2008) showed that stress shadows in global scale are present although they are rare and not so easily detectable.

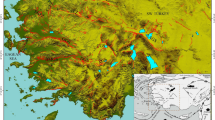
The purpose of the present study is to construct and apply a rate/state model in order to explore how the stress changes caused by successive strong main shocks perturb the seismicity rates in a region with a long history of devastating earthquakes. Our study area (Fig. 1) comprises western Turkey, one of the most rapidly deforming areas in Mediterranean, under the combined interaction of Eurasian, Arabian and African lithospheric plates and the involvement of the Aegean and Anatolia microplates. The most prominent tectonic characteristic of the broader area is the subduction and rollback of the Eastern Mediterranean oceanic lithosphere beneath the Aegean microplate along the Hellenic Arc since the early Miocene (Papazachos and Comninakis 1969, 1971), which has resulted to a significant N–S oriented extension regime in the Aegean and the adjacent areas. The second geodynamic process that affects the study area is the westward propagation of the Anatolian block away from the Arabian–Eurasian microplate collision zone along the North and East Anatolian Fault Systems (McKenzie 1972; Şengör et al. 1984; Bozkurt 2001). This geodynamic development is also confirmed by GPS studies (e.g., McClusky et al. 2000; Reilinger et al. 2006; Aktuğ et al. 2009). These interactions have produced a broad and complex system of normal faults, usually bounding the E–W trending extensional basins that are characteristically placed in parallel, with current rate of extension equal to 6 mm/year (McClusky et al. 2000; Nocquet 2012). Secondary structures with NE–SW trending basins are also evident (Taymaz and Price 1992; Westaway 1993). Dextral strike-slip faulting is dominant along the North Anatolian Fault (NAF), one of the longest active right-lateral fault systems, which extends for approximately 1,500 km, from eastern Turkey, through the Marmara Sea where it bifurcates into two subparallel branches.

Fig. 1
figure 1

Morphological map and main seismotectonic properties of the study area and its surroundings. Black lines indicate the major active boundaries: the subduction zone (Hellenic Arc) and the North Anatolian Fault—NAF with its westernmost extension, the North Aegean Trough (NAT). The collision zone between the Apulian and Eurasian plates along with the Rhodes Transform Fault—RTF and the Cephalonia Transform Fault—CTF at the southeastern and western termination of the Hellenic arc, respectively, are also indicated along with the Cyprus Arc at the southeast corner of the map. The white rectangle indicates the study area divided into 4 subareas

Full size image

Our attempt to contribute to the seismic hazard assessment is targeted on the future seismicity rates calculations, after considering previous seismicity and the evolution of the regional stress field. This becomes feasible owing to a homogeneous as far as the magnitudes are concerned catalog recently compiled (Leptokaropoulos et al. 2013) and the application of the rate/state model, previously mentioned. Full exploitation is also made of the stressing history of the major regional faults and static stress changes due to the stronger (M ≥ 5.8) that occurred in the study area since the early 1990s, when our calculations of the expected seismicity rates started. Physical parameters involved in the calculations are given various values, in an attempt to secure the results robustness. Therefore, despite the model simplifications and the uncertainties embodied in the calculations, the performance of the approach we followed led to satisfactory results in many of the study cases; especially when data number and time windows are adequate, the model was able to simulate up to 70–80 % of the real seismicity rate evolution.

2 Data

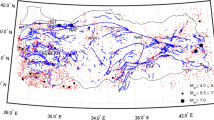
For investigating seismicity rate variation in association with the stress field evolution, the analysis needs to start as back in time as possible, usually limited by earthquake catalog availability and quality. Together with the epicentral uncertainties and depth errors, a major problem of the published regional catalogs is connected with the magnitude inhomogeneity, since different magnitude scales are assigned from different institutions and periods. To overcome this obstacle, we used an equivalent moment magnitude, \( M_{\text{w}}^{*} \), earthquake catalog, which was recently compiled by Leptokaropoulos et al. (2013), available at (ftp://geophysics.geo.auth.gr/pub/users/kleptoka/BSSA-D-12-00174-esupp.html) for our study area. This catalog includes earthquakes occurred during 1964–2010 with \( M_{\text{w}}^{*} \) ranging from 3.5 to 7.5, with the distribution of these events being nonhomogeneous in both space and time. Therefore, we divided the study area into four subareas (Fig. 2) exhibiting relatively uniform seismotectonic features (similar faulting type, seismicity level) and also similar data quality, as suggested by Leptokaropoulos et al. (2013).

Fig. 2
figure 2

Spatial distribution of earthquake epicenters during 1964–2010 in the study area with magnitudes expressed as \( M_{\text{w}}^{*} \). The 4 subareas (also indicated here) demonstrate different data density and completeness level. The fault plane solutions of M ≥ 5.8 events are shown as lower hemisphere equal-area projection, and their epicenters are depicted by stars

Full size image

The next task was to distinguish the starting point and duration of the reference and forecast periods for each region, in order to utilize as larger dataset as possible, for the seismicity rate analysis. We calculated the completeness magnitude, M C, for different time windows by applying the modified goodness-of-fit test proposed by Leptokaropoulos et al. (2013). This processing led to different starting year, number of events and M C for each subarea, as shown in Table 1. The reference seismicity rate periods were selected to last until the origin time of the first strong (\( M_{\text{w}}^{*} \) ≥ 5.8) event in Table 1. The testing periods were set to be equal with the inter-seismic periods between two successive main shocks in each study subarea. Nevertheless, the two 1999 (\( M_{\text{w}}^{*} \) > 7.0) events, occurred inside subarea 1, caused such large and extensive stress changes that significantly influenced seismicity rates also in subarea 4. Consequently, the ΔCFF associated with these events were also taken into consideration for the seismicity rate changes variation in this subarea. Note that instead of truncating the dataset by declustering, in order to avoid along-fault aftershock influence, we preferred using the entire dataset and focus our attention to specific target areas of major interest: Such areas are located close to the epicenter of the subsequent events or inside positive ΔCFF lobes (Toda and Stein 2003; Cocco et al. 2010; Leptokaropoulos et al. 2012).

Table 1 Properties of the datasets for each subarea
Full size table

3 Rate and state formulation

Following Dieterich (1994), the constitutive properties and system interactions that result in the onset of unstable slip must be defined in order to specify the time t, at which a particular source nucleates. This time is defined as:

$$ t = F\left( {C,\tau (t)} \right) $$
(1)

where C represents the initial conditions and τ(t) represents a stressing history. In general, the initial conditions, C, are a function of the nucleation sources, n, the reference seismicity rate, r, and the stressing rate, \( \dot{\tau }_{r} \). According to this rate/state stress transfer concept, earthquake nucleation controls the time and place of initiation of rupture, and therefore, the processes that alter earthquake nucleation times control changes in seismicity rates. Hence, there is a causative relationship between seismicity rate changes and stressing history. The changes in the rates of earthquake production depend on the coseismic stress perturbations, ΔCFF, the reference seismicity rates, the fault stressing rate and the constitutive fault properties, expressed by a dimensionless fault constitutive parameter, A. The modeled seismicity rate, R, is therefore given by Dieterich (1994):

$$ R = \frac{r}{{\gamma \cdot \dot{\tau }_{r} }} $$
(2)

where γ is the state variable for seismicity formulation that evolves with time and stressing history. Under a constant stressing rate, the initial value of state variable, γ 0 , is equal to the inverse value of \( \dot{\tau }_{r} \), and therefore, in the absence of a stress perturbation, the seismicity rate is equal to the reference rate. The evolution of the state variable is demonstrated as:

$$ d\gamma = \frac{1}{{{\rm A}\sigma }}(1 - \gamma \dot{\tau }_{r} )dt $$
(3)

In this equation, σ is the total normal stress. Product Aσ describes the instantaneous response of friction to a step change in slip speed (Toda and Stein 2003). If a strong earthquake occurs in the region, it alters the stress field and the state variable changes into a new value, γ n :

$$ \gamma_{n} = \gamma_{n - 1} e^{{ - \frac{\Delta CFF}{A\sigma }}} $$
(4)

where γ n−1 is equal to γ 0 for the first perturbation. Summarizing the former equations, it yields that the expected seismicity rate as a function of time, t, is given by:

$$ R\left( t \right) = \frac{r}{{\left[ {\exp \left( {\frac{ - \Delta CFF}{A\sigma }} \right) - 1} \right]\exp \left( {\frac{ - t}{{t_{a} }}} \right) + 1}} $$
(5)

In (4), ta is the characteristic relaxation time for the perturbation. The simulated seismicity rate values derived from this process are compared with real seismicity rates calculated for the respective time increments. Reference and observed seismicity rates at any inter-event time interval were translated into earthquake probabilities with the use of a probability density function (PDF). For the purpose of our study, the entire site was divided into 200 × 300 rectangular cells (with 2.7 km size each) constituting a normal grid and PDF determined the M ≥ M C earthquake probabilities at the center of each cell. The PDF used in the present study has the form (Silverman 1986):

$$ f(x,y) = \frac{1}{{nh^{2} }}\sum\limits_{i = 1}^{n} {K\left( {\frac{{x - X_{i} }}{h},\frac{{y - Y_{i} }}{h}} \right)} $$
(6)

where K stands for the Gaussian Kernel of the form:

$$ K(x,y) = \frac{1}{2\pi }e^{{ - \frac{{x^{2} + y^{2} }}{2}}} $$
(7)

with X i , Y i being the epicentral coordinates of the earthquakes (longitude, λ and latitude, φ, respectively), x, y the geographical coordinates of the centers of the bins, on which the value of PDF was estimated, n the number of the events, and h the bandwidth, having the same units with X i, Y i, x and y. From the former equations, the probability is derived as:

$$ P = \frac{1}{4n}\sum\limits_{i = 1}^{n} {\left[ {erf\left( {\frac{{y_{2} - Y_{i} }}{h\sqrt 2 }} \right) \cdot \left( {erf\left( {\frac{{ - x_{1} + X_{i} }}{h\sqrt 2 }} \right) - erf\left( {\frac{{ - x_{2} + X_{i} }}{h\sqrt 2 }} \right)} \right) + erf\left( {\frac{{y_{1} - Y_{i} }}{h\sqrt 2 }} \right) \cdot \left( {erf\left( {\frac{{ - x_{2} + X_{i} }}{h\sqrt 2 }} \right) - erf\left( {\frac{{ - x_{1} - X_{i} }}{h\sqrt 2 }} \right)} \right)} \right]} $$
(8)

with

$$ erf(x) = \frac{2}{\sqrt \pi }\int\limits_{0}^{x} e^{{ - t^{2} }} dt $$
(9)

The variables x 1, x 2, y 1, y 2, represent the boundaries of each cell (minimum and maximum longitude, minimum and maximum latitude, respectively).

4 Parameter values determination

In this section, we will debate on the selection/determination of the rest parameters values that are incorporated in the applied formulation.

4.1 Stressing rate

In our study, stressing rates were obtained from Paradisopoulou et al. (2010), who calculated \( \dot{\tau }_{r} \) as derived from slip rates in each fault segment, considered the seismic coupling (King et al. 2001) and concluded to values that were in agreement with those from Stein et al. (1997) and Parsons (2004). The average values computed for these segments were applied in the present study for each subarea, i.e., 0.10, 0.04, 0.025 and 0.03 bars/yr for subareas 1–4, respectively. Trials with additional stressing rate values were performed ranging from 0.04 to 0.25 bars/year for subarea 1 and 0.01–0.08 bars/year for the other three subareas, which represent the minimum and maximum values computed in each case.

4.2 Characteristic relaxation time and Aσ

Characteristic relaxation time, t a, also referred as aftershock duration, expresses the amount of time necessary to be elapsed until the rates of earthquake production restore to the rates that prevailed before the main event occurrence. Calculations were performed by considering t a fluctuation between 2.5 and 30 years. Dieterich (1994 ) pointed out that t a values range from 0.2 to 12 years for different regions worldwide, whereas Toda et al. (2005) estimated characteristic relaxation time varying from 7 to 66 years for various fault segments in southern California. Stressing rate and characteristic relaxation time are related to each other through the equation (Dieterich 1994; Dieterich and Kilgore 1996):

$$ A\sigma = t_{a} \cdot \dot{\tau }_{r} $$
(10)

In rate/state formulation, parameters A and σ always appear as a product. Moreover, due to the difficulties of calculating realistic values for these two parameters individually in the earth’s crust, Aσ is being estimated instead, which was found between 0.01 and 6 bars (Harris and Simpson 1998; Catalli et al. 2008), with values between 0.4 and 1 bars being more often applied in previous studies (Stein et al. 1997; Stein 1999; Belardinelli et al. 1999; Guatteri et al. 2001; Toda and Stein 2003; Toda et al. 2005; Ghimire et al. 2008). Because of lack of direct knowledge of rock physical properties values, we use the better determined seismological data, characteristic relaxation time and GPS data (for stressing rate) in a wide range, for incorporating and quantifying the rock properties. As a result, instead of selecting a single Aσ value, a wide span of 0.25–2.5 bars for subarea 1 and 0.15–1.2 bars for subareas 2, 3 and 4 is rather tested in this research, without of course studying in detail and directly the physical rock properties. Catalli et al. (2008) and Cocco et al. (2010) are some examples of previous works, which also simulated physical rock properties by tuning parameter Ασ.

4.3 Bandwidth

As shown in Eqs. 6 and 8, the value of probability density, P, is a function of the bandwidth (or window width), h, which represents the expanse of the area which is being influenced by each P value, and therefore, it determines the degree of smoothing. In general, high values of the window width represent better systematic variations, whereas lower values are usually set for revealing random local fluctuations. The bandwidth may have a single value, h, two values depending upon the x and y coordinates variance, h x and h y, respectively, or being adaptive when the smoothing is performed around each epicenter (rather than around each cell), and increases when the data become sparse (e.g., Helmstetter et al. 2006; Werner et al. 2010; Botev et al. 2010). In the present study, the division into four subareas was done by taking into account a relatively homogenous seismicity rate level, and therefore, we applied the first approach. Calculation of h x and h y provided identical values with the single value, in the 4 subareas, and therefore, the constant smoothing factor assumption could be applied with sufficiency. The applying values of bandwidth though fluctuate between 0.04° to 0.28°. Silverman’s (1986) formula for appropriate h estimation in respect of the data number and distribution provides values between 0.08 and 0.11 for the three subareas.

4.4 Coulomb stress changes

We model static stress changes ΔCFF by applying the apparent friction criterion which assumes:

$$ \Delta CFF = \Delta \tau + \mu {\prime } \cdot \Delta \sigma_{n} $$
(11)

where Δτ is the shear stress change in the direction of slip on the causative fault plane, Δσn is the normal stress change (assumed as positive for extension), and μ′ is the apparent coefficient of friction, including pore pressure effects and temporal changes in effective normal stress (Linker and Dieterich 1992; Simpson and Reasenberg 1994; Harris and Simpson 1998). Nostro et al. (2005) showed that this approach provides similar results with the isotropic poroelastic model (Beeler et al. 2000 ; Cocco and Rice 2002). According to this model, the pore pressure changes depend on the volumetric stress changes such that ΔP = −BΔσkk/3. Following this formulation, it yields that

$$ \Delta CFF = \Delta \tau + \mu \left( {\Delta \sigma_{n} - B\frac{{\Delta \sigma_{kk} }}{3}} \right) $$
(12)

where Δσkk is the alteration of the trace of the stress tensor, and B is the Skempton’s coefficient, which theoretically ranges from 0, for dry soil, to 1, for fully saturated soil. The apparent friction coefficient, μ′, is related to the above parameters as: μ′ = (μ − α) (1 − B), where α is the Linker and Dieterich (1992) parameter to account for the temporal changes in the effective normal stress. If in the fault zone Δσ11 = Δσ22 = Δσ33, so that Δσkk/3 = Δσ, then the apparent coefficient of friction is defined as μ′ = μ(1 − B). We adopted the value of μ′ = 0.4 as applied by Stein et al. (1997), Nalbant et al. (1998) and Paradisopoulou et al. (2010) for NAF and western Turkey. The Poisson’s ratio, ν, and shear modulus, G, were set equal to 0.25 and 3.3·105 bar, respectively.

All calculations were accomplished with respect to the focal mechanism and sense of slip of the next strong event. Fault plane solutions used for defining the rupture models of the strongest events come from various sources and are displayed in Table 2. The fault lengths, L, were estimated from the empirical relations of Papazachos et al. (2004), as they were specifically obtained for Aegean and surrounding areas. Fault widths, w, were estimated from the dip angle of the fault and the distance measured down–dip from the surface to the upper and lower edges of the rectangular dislocation plane, respectively, assuming that the seismogenic layer in the study area extends from 3 to 15 km depth (Papadimitriou and Sykes 2001; Paradisopoulou et al. 2010). Average coseismic slip, \( \bar{u} \), was calculated from the formula: \( M_{o} = G \cdot \bar{u} \cdot L \cdot w \), given the seismic moment, M 0, value (Table 2).

Table 2 Source parameters of the 12 earthquakes with M ≥ 5.8 modeled for coseismic static Coulomb stress changes calculations
Full size table

5 Simulated results

We present now the resulted seismicity rates for the forecasting periods, as derived from rate/state model application and their comparison with the observed ones for the respective periods. This comparison was also quantified by the means of Pearson linear correlation coefficient (PCC) and its 95 % confidence limits for a variety of combinations of parameter values. PCC is estimated in all cases for the entire dataset and once more for the data accommodated in areas experiencing positive Coulomb stress changes. This was done for two reasons. The first reason is that usually, most of the subsequent large earthquakes occur in such areas, a case that is confirmed in our study, since 9 out of 11 main shocks took place in positive ΔCFF areas. The second is that aftershocks to the fault of the triggering event inevitably occur in areas of apparent stress shadow because of the weakness of the applying rupture model to simulate stress changes in the near field. This apparent misfit is avoided by targeting on off-fault, positive ΔCFF areas.

In each subarea, a figure demonstrating the ratio of expected/observed seismicity rates is also provided (Figs. 3, 5, 7 and 9). Red colors overestimate excepted values in comparison with the real ones, whereas blue colors show underestimated expected values of seismicity rates. White areas correspond to ratio value between 0.5 and 2, suggesting sufficient model performance. Calculations are not performed in gray areas because of data insufficiency. Note that the comparisons were done for all the calculated pairs except those with extremely low values of seismicity rates (<0.001 events·cell/year), which correspond to areas with very low seismic activity, associated with minor faults or even large epicentral errors. This assumption provides statistically more robust results because the comparison of seismicity rates in relatively aseismic areas which exhibit different properties (such as bandwidth which quantifies the data density) is avoided. The quantification of the previously mentioned comparison is shown in Figs. 4, 6, 8 and 10 where the values of PCC along with their 95 % confidence intervals are demonstrated for the inter-event periods for different sets of parameter values.

Fig. 3
figure 3

Ratio of expected/observed seismicity rates for subarea 1, for 1999a–1999b (left frame Δt = 0.24 years) and 1999b–2010 (right frame Δt = 11.1 years). Parameter values applied are as follows: h = 0.08°, t a = 10 years and \( \dot{\tau }_{r} \) = 0.10 bar/year (Aσ = 1.0 bar)

Full size image
Fig. 4
figure 4

Pearson correlation coefficient (PCC) estimation (solid lines) and its 95 % confidence interval (dashed lines) for subarea 1. Upper frames were obtained from the entire dataset, whereas the lower frames yielded by taking into account only those cells experiencing positive ΔCFF. Bandwidth unit is degree (°), characteristic relaxation time unit is year (yr), and stressing rate unit is bar/year (bar/yr)

Full size image
Fig. 5
figure 5

Ratio of expected/observed seismicity rates for subarea 2, for 1992–2003 (upper left frame Δt = 10.4 years), 2003–2005a (upper right frame Δt = 2.5 years), 2005a–2005b (lower left frame Δt = 0.01 years) and 2005b–2010 (lower right frame Δt = 5.2 years), with h = 0.10°, t a = 15 years and \( \dot{\tau }_{r} \) = 0.04 bar/year (Aσ = 0.6 bar)

Full size image
Fig. 6
figure 6

Same as Fig. 4 but for subarea 2

Full size image
Fig. 7
figure 7

Ratio of expected/observed seismicity rates for subarea 3, for 1996–2008 (left frame Δt = 12 years) and 2008–2010 (right frame Δt = 2.4 years). Parameter values are taken to be: h = 0.10°, t a = 20 years and \( \dot{\tau }_{r} \) = 0.03 bar/year (Aσ = 0.6 bar)

Full size image
Fig. 8
figure 8

Same as Fig. 4 but for subarea 3

Full size image
Fig. 9
figure 9

Ratio of expected/observed seismicity rates for subarea 4, for 1995–1999a (upper left frame Δt = 3.8 years) and 1999b–2000 (upper right frame Δt = 1.3 years), 2000–2002b (lower left frame Δt = 1.1 years) and 2002b–2010 (lower right frame Δt = 8.9 years). Parameters values are taken as: h = 0.11°, t a = 20 year and \( \dot{\tau }_{r} \) = 0.03 bar/year (Aσ = 0.6 bar)

Full size image
Fig. 10
figure 10

Same as Fig. 4 but for subarea 4

Full size image

5.1 Subarea 1

The impact of two strong earthquakes (August 17, 1999, M7.6 and November 12, 1999, M7.2) on regional seismicity rates is studied here. As shown in Figs. 3 and 4, there is a poor observed/expected seismicity rate correlation for the ~100 days period between the occurrence of the two strong events. Nevertheless, it is evident in Fig. 4 that relatively high PCC values (>0.5) are achieved when characteristic relaxation time or stressing rate take lower values (<5 years and <0.05 bar/year, respectively). Given that the stressing rate is well constrained along the NAF with values usually much higher than 0.05, it follows from the model that t a may be lower than initially assumed. On the other hand, the second period (1999b–2010) demonstrates a much stronger correlation between real and modeled seismicity rate values, with PCC >0.7. Figure 3b shows that off-fault seismicity that took place west of the two main shocks rupture areas is well simulated by the rate/state model although some local deviations are still present. Note that the influence of these events is not modeled for the area beyond the 32 meridian due to the catalog geographical limitation. Finally, the results are identical if only positive ΔCFF bins are considered.

5.2 Subarea 2

Four strong events are considered for the rate/state modeling in this subarea: the November 6, 1992, M6.0, March 10, 2003, M5.8, October 17, 2005, M5.8 and October 20, 2005, M5.8 shocks. The forecasted periods correspond to the respective inter-seismic time intervals. Significant variations regarding the selection of parameter values are here observed (Figs. 5 and 6). The model seems to perform well for the first testing period, which has a quite long duration of over 10 years (Fig. 5a), but the PCC is notably lower regarding the subsequent, shorter periods (Fig. 6); especially for the third period, there is no linear correlation obtained during this 3-day time increment. Because of the high completeness threshold, it is necessary for a testing period to last for several years in order for the respective dataset to contain sufficient number of events. Correlation is though significantly improved when positive ΔCFF areas are only considered (Fig. 6, lower frames), and stressing rate together with characteristic time is a given lower value. Figure 5 evidences that expected rates are usually lower than the real ones, a fact that also suggests that the actual seismicity recovers faster at its reference level (1979–1992).

5.3 Subarea 3

Coseismic stress changes associated with July 20, 1996, M6.0 and July 15, 2008, M6.4 are incorporated to rate/state model for this subarea. The first period (1996–2008) exhibits high correlation coefficient, especially regarding the cells with positive Coulomb stress changes (Fig. 8). Although the next event occurred in stress shadow zone caused by the 1996 mainshock, the observed, smaller magnitude seismicity rates appear to correlate well with the simulated ones, with many cells having expected/observed seismicity rate ratio close to unity (Fig. 7a). The second period (2008–2010) exhibits almost no linear correlation. This is due to the short duration of the time interval (~2.5 years) and the respective small dataset (only 85 events) along with the depth uncertainties in this area. Note that the 2008 event and many of the following ones were located at depths larger than 30 km. Many cells that overestimate and underestimate real seismicity are both detected for this period.

5.4 Subarea 4

Four strong events occurred in this site since 1995: October 1, 1995, M6.3, December 15, 2000, M6.0 and two events that occurred on the February 3, 2002, with M6.4 and M5.8, respectively. These four events, together with the two strong 1999 earthquakes that took place in subarea 1, are consider to affect seismicity rates here. The first two periods studied (1995–1999 and 1999–2000) exhibit relatively strong correlation (PCC >0.5) when the entire dataset is considered (Fig. 10, upper frames). When calculations are performed only for positive ΔCFF cells (lower frames of Fig. 10), the first period (1995–1999) demonstrates even higher efficiency, whereas the second one fails to describe at all seismicity that occurred in positive stress lobes. This is one of the rare cases that rate/state model performs better in stress shadows rather than modeling seismicity enhancements. This may be probably because of the short duration (1.3 years) of this testing period (mostly concerning aftershock productivity), which was abruptly interrupted from the 2000 event. The other two periods studied (2000–2002 and 2002–2010) demonstrate low correlation, which becomes slightly higher for positive ΔCFF (Fig. 10). Once again the model performance is getting better as we go toward lower t a values (<10 years). Note that in second and third periods (1999–2000 and 2000–2002), the available data are so sparse that calculations have only been performed for approximately half of the entire area. The last period (2002–2010) actually shows many cells with comparable observed and expected seismicity rates, but there are still several bins with large differences which reduce the total correlation coefficient although the simulation is adequate for a considerable part of the region (Fig. 9d). The actual PCC for the cells with ratio between 0.4 and 2.5, which occupy half of the area’s cells with calculated values, is 0.864.

6 Discussion and concluding remarks

We conclude this study by highlighting and discussing some of the most important issues regarding the applied methodology and its constraints in parameters selection. Concerning the bandwidth, higher values of h result in higher correlation but from physical aspect, too high values should be avoided because they oversmooth seismicity patterns and balance the differences among broader areas leading to erroneous results. On the contrary, smaller values are preferable because in such way each earthquake has a limited area of influence, and consequently, low seismicity areas should be better distinguished. Regarding the rate/state parameters, the model seems to perform better when lower Ασ values are applied. This in turn means that lower values of the selected range of t a or \( \dot{\tau }_{r} \) are more appropriate. Stressing rate has been determined with sufficient accuracy, since many studies can confirm, and thus, it is very unlikely for \( \dot{\tau }_{r} \) having values almost one order of magnitude lower. Hence, a probable scenario is that in the study region, the constitutive properties of the fault zones exhibit lower Ασ values and consequently lower characteristic relaxation time (Eq. 10). These results seem to be in better agreement with Dieterich (1994) who estimate t a varying between 0.5 and 5 years in some cases, putting into question the selection of higher t a values, as stated in the literature, for application in our study area. In addition, it is also shown in our trials that the previously mentioned parameter values usually have a negligible impact on the resulting correlation. This is due to the fact that these parameters amplify or depress seismicity rates expected but do not influence their spatial pattern, a property that almost exclusively depend on reference seismicity rate, stress changes and bandwidth selection.

The parameter values depend on physical rock properties, which can be nonuniform over the area. Catalli et al. (2008) pointed out that although it is likely to expect that all of the considered parameters are spatially variable, it is extremely difficult to constrain realistic patterns for rate/state modeling. This is the main reason for considering these parameters as spatially uniform and constant in most of the applications available in the literature. At this point, we should emphasize that the explicit determination of physical rock properties is not an issue of this study. In general, these values are not known and have to be estimated from the observed seismicity data or using some approximate physical relations (Hainzl et al. 2009). Dieterich (1994) formulation’s actual power is lying upon indirectly incorporating these properties despite the uncertainties that they exhibit in order to simulate and forecast seismicity rate changes. Toda et al. (1998), for example, estimated Aσ by fitting the observed dependence of the seismicity rate change (R/r) on stress change predicted for rate/state-dependent fault properties, i.e., by using indirect mean instead of recalling laboratory experimental results. The model parameters are strongly correlated with each other for both physical and statistical reasons, and in this study, it is verified that different sets of model parameters can yield to the same expected seismicity rate variations, in agreement with Cocco et al. (2010).

Another issue of discussion arises from the calculated values of coseismic ΔCFF, thoroughly presented in the "Appendix". It is commonly accepted that an empirical threshold of 0.1 bars is usually assumed to trigger seismicity (indicated by isolines in "Appendix" figures). We took into consideration the coseismic stress changes due to the 1999 Izmit and Düzce earthquakes for calculations in subarea 4. As shown in Appendix Fig. 11d and e, these stress changes are less than the aforementioned threshold of 0.1 bars. On the other hand, Hardebeck et al. (1998) suggested that any small stress change is capable of triggering and the existence of an apparent minimum triggering stress is connected with the sufficient number of triggered events to be detectable with dataset used. Ziv and Rubin (2000) also point out that triggering is not a threshold process, whereas Ogata (2005) showed that even small size of CFS increment down to the order of millibars can trigger activation and lowering of microseismicity, opposing to other studies supporting that there should be a threshold value of DCFS capable of affecting seismic changes. Nevertheless, the point here is that we do not claim that these changes cause seismicity rates to rise or depress. According to rate/state formulation, ΔCFF is only one parameter together with reference seismicity rate, stressing rate and characteristic relaxation time. ΔCFF may not alone induce extraordinary seismic activity, but the combination of all the parameters incorporating to the model may result in significant triggering or rate decrease.

Fig. 11
figure 11figure 11figure 11figure 11

Static Coulomb stress changes associated with M ≥ 5.8 earthquakes that took place in the study area and were incorporated in rate/state modeling (Table 2). Fault plane solutions of these events are plotted as lower hemisphere equal-area projections and the numbers indicate the rank of occurrence. The straight lines indicate the boundaries of the 4 subareas, whereas the isolines of −0.1 and 0.1 bars are indicated by black curves inside the stress lobes. a Static stress changes due to the November 6, 1992, event in the entire study site (left frame) and in its close vicinity (right frame). b Static stress changes due to the October 1, 1995, event in the entire study site (left frame) and in its close vicinity (right frame). c Static stress changes due to the July 20, 1996, event in the entire study site (left frame) and in its close vicinity (right frame). d Static stress changes due to the August 17 and November 12, 1999, events in the entire study site. The resolution of the stress field is done according to the focal mechanism of the November 12, 1999, event. e Static stress changes due to the August 17 and November 12, 1999, events in the entire study site. The resolution of the stress field is done according to the focal mechanism of the December 15, 2000, event (subarea 4). f Static stress changes due to the December 15, 2000, event in the entire study site (left frame) and in its close vicinity (right frame). g Static stress changes due to the February 3, 2002(a), event in the entire study site (left frame) and in its close vicinity (right frame). h Static stress changes due to the February 3, 2002(a), event in the entire study site (left frame) and in its close vicinity (right frame). i Static stress changes due to the March 10, 2003, event in the entire study site (left frame) and in its close vicinity (right frame). j Static stress changes due to the October 17, 2005, event in the entire study site (left frame) and in its close vicinity (right frame). k Static stress changes due to the October 20, 2005, event in the entire study site (left frame) and in its close vicinity (right frame). l Static stress changes due to the July 15, 2008, event in the entire study site (left frame) and in its close vicinity (right frame)

Full size image

The methodology we followed provided satisfactory results in general, if we take into account the uncertainties, assumptions and simplifications that we considered in order to construct a more flexible and easy to apply model. The uncertainties arise from the accuracy in determination of the focal coordinates of the earthquakes used in the current analysis. They are also related with the parameter values speculation although a wide range of them was considered. Different kind of uncertainties embodied in our study deal with the determination of the rupture models, especially of the smaller magnitudes main shocks. Moreover, strong event influence (e.g., 1956 M = 7.7 in southern Aegean, 1967 M = 7.2 in NAF, 1970 M = 7.1 close to the borders of subareas 2 and 4) was not taken into account because of the insufficient data available before 1980 for a robust seismicity rate investigation. Therefore, it is inevitable that the state of stress remains unknown at the beginning of our analysis, since data adequacy and reliability reduce when going back in time (e.g., Papadimitriou and Sykes 2001). Nevertheless, note that we utilized nondeclustered datasets, which contain triggered events or seismicity depression that persist in time and are related to the stress perturbations produced by previous strong main shocks (Leptokaropoulos et al. 2012). Therefore, the reference seismicity rates pattern contain in a way some of the effects associated with these nonmodeled stress perturbations.

In this study, we followed a simple model to forecast seismicity rate changes, and then, we quantified the efficiency of this model. Consequently, the influence of other physical processes such as postseismic deformation, viscoelastic relaxation and rheological properties was also neglected. For example, recent investigations of Wang et al. (2009, 2010, 2012) suggest a strong influence of the after-slip, besides the aftershocks considered and viscoelastic deformation on the development of the stress distribution. They performed their analysis in the 1999 Izmit aftershock sequence (NAF) and in the sequence followed the 2004 Parkfield earthquake in southern California. Their results showed that early postseismic displacements following the main shocks can be in principal explained by stress-driven creep in response to coseismic stress perturbations, and the large aftershocks located in the zone loaded by the main shock. According to their analysis, the observed postseismic displacements decay slower than the aftershock seismicity postseismic activities (including aseismic relaxation and large aftershocks), and they can be reasonably explained by stress relaxation processes in the deeper ductile layer. The interaction among the aftershocks, the variability of their focal mechanisms and the poorly determined ΔCFF in the near field introduce additional uncertainties in the applied procedure.

Summarizing, the model applied in this study seems to provide promising results, as it was able to forecast in several cases future seismicity rates in spite of the aforementioned assumptions and uncertainties. The crucial point is that adequate data are needed in order to obtain robust results and that is where the actual power of rate/state model lies: taking advantage of well-constrained natural quantities, together with high accuracy seismic data in order to determine the boundaries of parameters that cannot be directly measured and predict the impending activity. Nevertheless, even under these circumstances and the simplifications and uncertainties presented above, the present study substantiates that a very simple forecasting model can sufficiently approximate the natural processes as previous researches have shown and provide satisfactory results even when minor size dataset is used.