Abstract
We report here on the observation and offline detection of the meteotsunami off the New Jersey coast on June 13, 2013, using coastal radar systems and tide gauges. This work extends the previous observations of tsunamis originating in Japan and Indonesia. The radars observed the meteotsunami 23 km offshore, 47 min before it arrived at the coast. Subsequent observations showed it moving onshore. The neighboring tide gauge height reading provides confirmation of the radar observations near the shore.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
An unusual storm system moved eastward across the country on June 13, 2013, commonly called a “derecho”, and appears to have launched a meteotsunami that impacted the US East Coast. Meteotsunamis occur frequently in the Mediterranean region (Adriatic, Aegean, and Black Seas) (Renault et al. 2011; Vilibic´ et al. 2008), but are rarely mentioned in the USA. The existence of the meteotsunami was confirmed by several of the 30 tide gauges along the East Coast up through New England and was seen as far away as Puerto Rico and Bermuda. A NOAA DART buoy was triggered by the event, as well as another bottom-pressure sensor-of-opportunity in the region, a Sonardyne bottom-pressure recording (Hammond 2013). All of these outputs give a measure of the meteotsunami height.
The event, which occurred during daylight hours, attracted widespread attention after several media reports were released focusing on local impacts including people being swept off a breakwater at Barnegat Light, NJ, some damage to boat moorings, and minor inundation.
Although the origins of meteotsunamis vis-a-vis seismically generated tsunamis differ, the propagation and evolution of these shallow-water waves are the same, as are the applicable detection and warning methods. In Sect. 3, we describe the general mechanism for the generation of meteotsunamis.
A tsunami is a shallow-water wave, implying that the depth determines its properties and how they evolve. A high-frequency (HF) radar measures its orbital velocity, not its height. The orbital velocity of a single traveling wave at its crest moves in the direction of wave propagation; at its trough, the velocity opposes that direction. The radar maps the velocity with distance from the shore. Most other sensors provide point measurements. The radar mapping distance depends on bathymetry and tsunami strength. For the orbital velocity observed by the radar as a current flow, a single radar is adequate. However, multiple sites producing 2D maps give a complete picture of the near-field dynamics.
Tsunami warning systems presently in place rely primarily on computer models. They provide warning of earthquake-generated tsunami impacts and predict their strength and arrival times versus location based on the earthquake characteristics, subsequent sensor detections, e.g., from DART buoys, and forecast models. Earthquake information and tsunami model predictions are disseminated rapidly after dangerous earthquakes. Operational radar systems with software that can detect an incoming tsunami with a significant warning capability are only now being deployed. Tide gauge sea levels at coastal positions closer to the epicenter can provide useful information on water levels for locations further downstream, if they are able to transmit data after detection. The 2011 Japan tsunami signal was observed by many HF radars (SeaSonde 2013) around the Pacific Rim with clear results from sites in Japan and the USA (Lipa et al. 2011, 2012a). The 2012 Indonesia tsunami was observed by radars (SeaSonde 2013) on the coasts of Sumatra and the Andaman Islands (Lipa et al. 2012b). In addition to their primary operational purpose of observing real-time offshore circulation, radars equipped with tsunami detection software can also provide local quantitative tsunami information and warning as the wave approaches.
We have demonstrated an empirical method for the automatic detection of a tsunami based on pattern recognition in time series of tsunami-generated current velocities, using data measured by seventeen radars (Lipa et al. 2012a, b). Such HF radar systems presently operate continuously from many coastal locations around the globe, monitoring ocean surface currents and waves.
In this paper, we examine June 13, 2013, data from three HF radars on the New Jersey coast and show that the measured current velocities display the characteristic tsunami signature, allowing the detection of the meteotsunami, initially well offshore. For the first time, these data provide detection time as a function of range. Radar-observed detection times are compared with tide gauge observations and with that predicted from the phase speed of the meteotsunami, which depends on depth alone.
2 Theoretical analysis
The Navier–Stokes equation and the equation of continuity form the basis for tsunami modeling. Barrick (1979) derived closed-form expressions for tsunami parameters, based on linear wave theory, assuming piecewise constant depths and a sinusoidal profile for the tsunami. We present some of these equations here.
For shallow-water waves like tsunamis, the phase velocity, v ph(d), for depth d is given by
where g is the acceleration due to gravity. The height, h(d), of the tsunami is expressed in terms of its value in deep water, which was taken to have a depth of 4,000 m:
where \(h_{4000}\), the height of the tsunami in deep water, and d are expressed in meters. The maximum surface orbital or particle velocity is given by
The time for the tsunami to cover a distance L terminating at the radar site is given in terms of the phase velocity by
For a tsunami, the phase/group velocity of the wave is much faster than the maximum orbital velocity, but from (1), it slows down in shallow water as d 1/2, increasing the warning available from the time of detection. From (2) and (3), the height increases as d −1/4, while the maximum particle velocity increases more quickly as d −3/4, increasing the signal seen by the radar.
3 Origin of meteotsunamis and nature of June 13, 2013, event
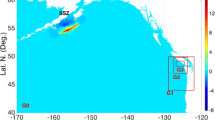
A meteotsunami is generated by an atmospheric pressure disturbance traveling across the sea (Renault et al. 2011; Vilibic´ et al. 2008; Monserrat and Thorpe 1996; Rabinovich and Monserrat 1996; Monserrat et al. 2006; Asano et al. 2012). Explained simply, a low-/high-pressure center (or edge) moving at a given velocity attempts to produce a peak/trough under it on the sea traveling at the same speed. This can generate a freely propagating surface gravity wave that increases in amplitude when the speed of the atmospheric anomaly v aa matches the phase velocity of a shallow-water wave v ph(d) given by (1). The June 13, 2013, “derecho” event traveled at about 21.1 m/s or 76 km/h (Hammond 2013). As the speed v aa is equal to v ph(d), it follows that the depth d at which “resonance” or onset of independent wave launching occurs is 45 m. This depth region lies about 60 km off the New Jersey coast (refer to Fig. 1).
Meteotsunamis generally do not have sufficient heights/energies to cause catastrophic loss of life, as do severe seismic tsunamis, although damage to harbors and coastal structures is frequently significant. Few in the USA are even aware of the term “meteotsunami” although these events indeed do occur along our coasts. However, meteotsunamis have been reported for North America in the scientific literature, in particular for the East Coast (Sallenger et al. 1995; Churchill et al. 1995; Mercer et al. 2002; Pasquet and Vilibić 2013; Vilibić et al. 2013).
This June 13, 2013, event, however, attracted significant attention among many agencies and scientific groups that may have been lacking for prior, more localized incidents. Perhaps this resulted from the fact that it was seen from New England through Southern New Jersey, and as far away as Puerto Rico. A scientific team was convened (Hammond 2013). Their analysis and collaboration are ongoing, this paper being one of several that are in process.
The unique characteristic of this meteotsunami is that it was generated by a frontal pressure anomaly traveling eastward, i.e., offshore. Yet it was seen by coastal sensors including HF radars as approaching the coast. How is this possible? The models reported by Hammond (2013) show that a strong reflection occurs at the edge of the shelf, about 110–120 km offshore. There, the depth drops from about 100–1,200 m over the space of about 20 km. The reflection coefficient is greater when the wave travel approaches a drop-off rather than a step-up with the same slope. Radar data presented here confirm the existence of a wave reflected back toward the New Jersey coast.
We now describe what happens when the tsunami interacts with a hard boundary. Consider a single “soliton” Gaussian pulse of water approaching the coast; it is a traveling wave, with its forward velocity maximum at the crest. As a wall/hard boundary is approached, the height will double and the velocity must become zero. Then, at some time after the reflection, there is a solitary wave traveling backward again, with the crest velocity maximum in phase with the height crest.
What has happened at the wall? The velocity is zero but height is at a maximum. The velocity must flow toward the wall before mass transport builds up the height of the water. When the water height reaches its maximum at the wall, the velocity becomes zero. Then, gravity forces the water to flow away from the wall and the height begins to decrease, slowly at first, then more rapidly as the relaxation of the water peak accelerates.
In reality, the situation is more complex, but it can be seen that as a result of this boundary effect, the height wave approaching the coast (as seen by a tide gauge) will lag the velocity wave seen by a radar by as much as a quarter cycle.
4 HF radar tsunami detection
For tsunami detection, a transmit frequency >10 MHz is preferred, as having greater time, space, and velocity resolution.
4.1 History
Barrick (1979) originally proposed the use of shore-based HF radar systems for tsunami warning. Lipa et al. (2006) described a simulation that superimposed modeled tsunami-induced currents at the end of the HF radar processing chain and proposed a detection method based on these simulations.
The analysis described by Lipa et al. (2006) was based on simulated tsunami currents, which at that time were the only data available. Since then, we have accumulated a database of actual HF radar tsunami observations from both strong (Japan 2011) and weak (Indonesia 2012) tsunamis that have been used to identify the tsunami signature in current velocities and test automatic detection methods.
4.2 Factors affecting detectability
-
1.
As a traveling tsunami wave approaches the coast over a shelf with decreasing depth, as discussed in Sect. 2, its orbital velocity increases as the d −3/4, while the amplitude increases as d −1/4. Thus, the velocity increases more sharply than does the depth, which gives advantage to the radar sensor. At the depth decreases, the orbital velocity exceeds a detection threshold.
-
2.
The orbital velocity and amplitude, being locked together, of course depend on the severity of the tsunami, and this is a second factor determining detectability.
-
3.
Finally, the orbital tsunami current must be detected among the ambient background flow. There are two types of current with which it must contend for detectability:
-
a.
A mean flow, for example, due to tides, geostrophic effects. We have considered and employ a variety of means to filter out or mitigate these effects.
-
b.
A sub-grid-scale random current variability, seen in the surface currents by the radar as well as drifters. This random variability is the ultimate limitation and cannot be filtered out over the short time scales during which tsunamis must be detected. It is variable depending on location. For example, on the East Coast off New Jersey, we find it is about 5 cm/s, while in the Pacific off the West Coast, it is approximately 12 cm/s (Hubbard et al. 2013).
-
a.
Tsunamis with orbital velocity amplitudes of 5 cm/s have been detected (Lipa et al. 2012a, b). Taking the above factors into account, and based on our past cited experience with moderate tsunami heights in deep water, we find the 200-m isobath to be a convenient—albeit approximate—onset demarcation for likely detectability.
5 Data sets
We analyzed data sets from three SeaSonde HF radar systems located at Brant Beach (BRNT), Brigantine (BRMR), and Belmar (BELM), New Jersey. These radars stored data in a form suitable for tsunami analysis. Raw radar spectra files for June 13, 2013, with a 2-min time resolution were averaged in pairs, resulting in 4-min temporal outputs. Radar transmit frequencies and range cell widths were approximately 13.5 MHZ and 3 km, respectively. Radar system specifications are available online (SeaSonde 2013).
Radar results were compared with data from NOAA tide gauges at Atlantic City and Sandy Hook, NJ. Graphics of the tide gauges were obtained from the file SeaLevel06132013.pdf downloaded from the NOAA website: http://ntwc.arh.noaa.gov/about/
Figure 1 shows the locations of the radars and tide gauges, and the offshore bathymetry. The meteotsunami height at the neighboring DART buoy was small (5 cm) (Hammond 2013).
6 Methods
In the following text, we use the term “arrival” to signify the first tsunami detection. Methods used to produce velocity components for analysis have been described previously (Lipa et al. 2012a). To summarize, (a) short-term radar cross-spectra (4-min time outputs) are analyzed to give radial velocities; (b) radial velocities in narrow rectangular area bands approximately parallel to the depth contours are resolved parallel and perpendicular to the depth contour; (c) these velocity components are averaged within each band to reduce the noise that is inherent in velocities derived from short 4-min spectra; (d) time series of the average velocity components (termed area-band velocities) are formed.
For tsunami observations, two effects distinguish the area-band velocities from the background: First, after arrival within the area monitored, velocities in neighboring bands are strongly correlated and second, the oscillation magnitudes deviate significantly from background values. We use a pattern detection procedure extended from that developed for the Japan tsunami (Lipa et al. 2012a) to calculate a factor (termed the q-factor) that signals the tsunami arrival when it exceeds a preset threshold.
An empirical pattern detection procedure has been developed, based on signal characteristics. The following data set is analyzed: Velocity components v b (t) at three adjacent times and five area bands, b, within the coverage area are selected for tsunami detection. At a given time t, three quantities (q 1, q 2, and q 3) are calculated as running sums over different area-band combinations. Initially, they are set to zero. Based on experimentation with measured tsunami data, three augmentation factors Δq 1, Δq 2, and Δq 3 and three limits L 1, L 2, and L 3 on velocity increments have been defined and are preset.
-
(1)
Calculation of q 1
For each band at time t, the change in velocity Δv b (t) over two adjacent time intervals is calculated, i.e., Δv b (t) = v b (t)−v b (t−2δ), where δ is the time spacing. If this is less than −L 1 (velocity is decreasing), q 1 is augmented by −Δq 1. If it is greater than L 1 (velocity is increasing), q 1 is augmented by +Δq 1.
-
(2)
Calculation of q 2
The times defining maximum/minimum velocities over a sliding time window are found for each band. If the minimum values for different bands coincide, q 2 is augmented by −Δq 2. If the maximum values for different bands coincide, q 2 is augmented by +Δq 2.
-
(3)
Calculation of q 3
If the velocity increases/decreases with time for three area bands from t−2δ to t−δ and from t−δ to t, q 3 is augmented by +Δq 3/−Δq 3.
The final q-factor is the product of q 1, q 2, and q 3; tsunami arrival is signaled when the value of q exceeds a preset threshold. Positive/negative values indicate the tsunami is moving toward/away from the radar.
To set the threshold, q-factors are obtained from an extended data set, in order to determine typical values under normal conditions. There is a trade-off in selecting the threshold value. Too small a value will result in many false alarms. To detect small tsunamis (like this meteotsunami), the threshold is set a factor of 10 higher than typical values. For this study, the threshold was set to 50. For the 2011 Japan tsunami, it was set to 500 (Lipa et al. 2012a). The tsunami signal can be evident for some time after arrival; however, this detection method is optimized to apply to the first arrival. These detection methods were applied offline.
7 Results
7.1 Tide gauge water levels
Tide gauge data are shown in Fig. 2. Readings at Atlantic City show the maximum negative meteotsunami signal at approximately 18:42 UTC, indicated by the sharp water level decrease. This is followed at approximately 22:00 UTC by a sharp increase in water level and subsequent oscillations. The effects of the meteotsunami on the Sandy Hook water level are much less, with the arrival barely noticeable.
NOAA tide gauge observations June 13, 2013, a Sandy Hook, NJ. b Atlantic City, NJ. Graphics of the tide gauges were obtained from the file SeaLevel06132013.pdf, which was downloaded from the NOAA website: http://ntwc.arh.noaa.gov/about/
7.2 Radar current velocity observations
7.2.1 Unfiltered area-band velocities
As described in Sect. 6, radial velocities in rectangular area bands 2 km wide approximately parallel to the depth contours were resolved along and across the depth contour and averaged within each band. The tsunami arrival is indicated by a marked drop in the perpendicular velocity component and correlation in time between different area bands. No tsunami signature was observed in the parallel component.
Figure 3 shows the BRNT, BRMR perpendicular velocity components at four area bands, and the generated q-detection factors, which were derived from all the area bands. The velocity decreases at the tsunami arrival (Fig. 3) as is also indicated by the closest tide gauge at Atlantic City.
Radar observations of the tsunami arrival. Area-band velocity components versus time (hours UTC from June 13, 2013, 00:00) Negative velocity means water is moving offshore: BRNT a blue 6–8 km; red 8–10 km; b black 10–12 km; green 12–14 km. c The q-factor detection. BRMR d blue 2–4 km; red 6–8 km; e black 14–16 km; green 20–22 km. f The q-factor detection
Velocities at BELM (Fig. 4) show much less tsunami signal, with the weak signal evident in only two area bands. This is consistent with tide gauge measurements at Sandy Hook, 30 km to the North, which barely registered the tsunami arrival. The tsunami signal at BELM was too weak to trigger a tsunami detection.
About 4 h later, after 22:00 UTC, BRNT velocities first increase and then sharply decrease (Fig. 5), as is also shown by the Atlantic City tide gauge. This effect was not seen at BRMR or BELM.
7.2.2 Filtered area-band velocities
In order to illustrate more clearly the approach of the first meteotsunami velocity trough onto the coast, the BRNT area-band velocities shown in Fig. 3 were processed as follows:
-
1.
The velocity time series were detrended to remove variations with scales longer than 1.5 h, getting rid of tides and other longer-term slopes. This was done by fitting a constant and linear trend to the data for a 1.5-h time period before the tsunami began and subtracting this from the data that included the tsunami.
-
2.
The data were then low-pass-filtered with a three-point (12-min) non-causal algorithm, in this case, the MATLAB “filtfilt” function. This eliminates the non-symmetric lag inherent in causal filters and minimizes end effects.
-
3.
The resulting time series from two consecutive bathymetry-parallel bands were averaged to further reduce the inherent random signal variations.
Results are shown in Fig. 6, where the subplots are the smoothed signals as a function of time for different distances from shore. The dashed line illustrates the progression of the first tsunami trough versus time and distance. The time–distance progression of the shoreward-moving event was confirmed by tsunami hindcast modeling discussed and presented by Hammond (2013).
7.3 Tsunami arrival times versus distance from shore
7.3.1 Radar-observed arrival times from orbital velocities
The velocity plots in Figs. 3 and 4 indicate that the tsunami arrives earliest in the most distant range cells and later as shore is approached. Fig. 7a shows arrival times versus distance from shore for the radars (defined to correspond to the minimum velocity value) and the Atlantic City tide gauge (defined to correspond to the minimum water level).
a The radar-observed arrival time (hours UTC from June 13, 2013, 00:00) of the first tsunami trough versus distance from shore. Red asterisk Atlantic City tide gauge; Radar: Blue BRNT, Black BRMR, Green BELM, Magenta Tsunami arrival time calculated from the phase speed of a traveling tsunami trough, calculated from (4) based on initial detection at 23 km; b Approximate depth versus distance from BRNT perpendicular to the shore
7.3.2 Calculated arrival times from the phase speed of the traveling tsunami trough
The arrival time of the minimum wave height trough at BRNT in the absence of a coastal boundary was calculated from (4). In shallow water, this differs from the radar-observed arrival times resulting from the orbital velocity. The depth offshore from BRNT shown in Fig. 1 was approximated by parallel contours, which was considered reasonable given that small-scale depth features are naturally low-pass-filtered on a scale of the tsunami wavelength. The solid curve in Fig. 7a shows the calculated arrival times at BRNT plotted as a function of distance offshore. The approximate depth versus distance from shore is plotted in Fig. 7b.
Figure 7a indicates that the meteotsunami arrived 23 km off BRNT and BRMR at approximately the same time and then to moved toward shore at about 30 km/h (average speed over all points). The meteotsunami arrived 23 km off BELM about 14 min later. From the two readings, it appears to move toward shore at a higher speed, probably because the water is deeper close to the Hudson Canyon. The first observation of the tsunami at BRNT occurred 47 min before its arrival at the Atlantic City tide gauge.
8 Discussion and conclusions
Sources of uncertainty in the results presented here include noise in radar and tide gauge results, approximations in specifying depths contours, and the fact that the tide gauge is located 35 km from BRNT.
As discussed in Sect. 3, as the coast is approached, the maximum height wave lags the velocity maximum. This time difference is confirmed in Fig. 7: The arrival of the tsunami at the tide gauge lags the radar-observed arrival.
Although the calculated arrival time is set to be the same as the radar-observed time at the distance of 23 km, the curves diverge as the coast is approached, with the radar-observed time lagging (Fig. 7). This is because the calculation assumes a pure traveling wave and no interaction with the coastal boundary, while the radar-observed times are affected by the boundary. The arrival of the tsunami at the tide gauge lags both radar-observed and calculated arrival times close to the coast.
The coastal boundary explains why the trough velocity closest to the shore shown in Fig. 6 is smaller than at greater distances: The hard boundary forces normal velocity to zero while doubling the height at the boundary from that at greater distances from shore, as discussed in Sect. 3.
The first tsunami signal deviation was a “trough”. The SeaSonde-observed velocity was offshore, and the closest tide gauge at Atlantic City also saw a trough (depression). Nonetheless, although the velocity at this trough was flowing offshore, the wave itself was approaching the coast, as confirmed by the wave pattern propagating through the range cells shown in Fig. 6. As discussed in Sect. 3, this is due to a strong reflection occurring at the edge of the shelf, about 110–120 km offshore.
The radars observed the tsunami up to 23 km offshore, 47 min before it arrived at the coast. The tide gauge height reading provides confirmation of the radar observations at the shore and indicates the successful detection of a meteotsunami with a wave height of less than 50 cm. It also suggests that as much as a half hour warning alert can be provided by HF radar under similar tsunami height and bathymetry conditions before the wave strikes the shore.
References
Asano T, Yamashiro T, Nishimura N (2012) Field observations of meteotsunami locally called “abiki” in Urauchi Bay, Kami-Koshi Island, Japan. Nat Hazards 64:1685–1706
Barrick D (1979) A coastal radar system for tsunami warning. Remote Sens Environ 8:353–358
Churchill DD, Houston SH, Bond NA (1995) The Daytona Beach wave of 3–4 July 1992: a shallow water gravity wave forced by a propagating squall line. Bull Am Meteorol Soc 76:21–32
Hammond S (2013) Teleconference on Meteotsunami, July 18, Chaired by Steve Hammond, NOAA. http://nctr.pmel.noaa.gov/eastcoast20130613/
Hubbard M, Barrick D, Garfield N, Pettigrew J, Ohlmann C, Gough M (2013) A new method for estimating high-frequency radar error using data from Central San Francisco Bay. Ocean Sci J 48(1):105–116
Lipa B, Barrick D, Bourg J, Nyden B (2006) HF radar detection of tsunamis. J Oceanogr 2:705–716
Lipa B, Barrick D, Saitoh S-I, Ishikawa Y, Awaji T, Largier J, Garfield N (2011) Japan tsunami current flows observed by HF radars on two continents. Remote Sens 3:1663–1679
Lipa B, Isaacson J, Nyden B, Barrick D (2012a) Tsunami arrival detection with high frequency (HF) radar. Remote Sens 4:1448–1461
Lipa B, Barrick D, Diposaptono S, Isaacson J, Jena BK, Nyden B, Rajesh K, Kumar TS (2012b) High Frequency (HF) Radar detection of the weak 2012 Indonesian tsunamis. Remote Sens 4:2944–2956
Mercer D, Sheng J, Greatbatch RJ, Bobanović J (2002) Barotropic waves generated by storms moving rapidly over shallow water. J Geophys Res 107(C10):3152. doi:10.1029/2001JC001140
Monserrat S, Thorpe AJ (1996) Use of ducting theory in an observed case of gravity waves. J Atmos Sci 53(12):1724–1736
Monserrat S, Vilibić I, Rabinovich AB (2006) Meteotsunamis: atmospherically induced destructive ocean waves in the tsunami frequency band. Nat Hazards 6:1035–1051
Pasquet S, Vilibić I (2013) Shelf edge reflection of atmospherically generated long ocean waves along the central US East Coast. Cont Shelf Res 66:1–8
Rabinovich AB, Monserrat S (1996) Meteorological tsunamis near the Balearic and Kuril islands: descriptive and statistical analysis. Nat Hazards 13:55–90
Renault L, Vizoso G, Jansà A, Wilkin J, Tintoré J (2011) Toward the predictability of meteotsunamis in the Balearic Sea using regional nested atmosphere and ocean models. Geophys Res Lett 38:L10601
Sallenger AH Jr, List JH, Gelfenbaum G, Stumpf RP, Hansen M (1995) Large wave at Daytona Beach, Florida, explained as a squall-line surge. J Coastal Res 11:1383–1388
SeaSonde (2013) Codar Ocean Sensors. Available online. http://www.codar.com/SeaSonde.shtml
Vilibić I, Monserrat S, Rabinovich A, Mihanović H (2008) Numerical modeling of a destructive meteotsunami of 15 June, 2006 on the coast of the Balearic Islands. Pure Appl Geophys 165:2169–2195
Vilibić I, Horvath K, Strelec Mahović N, Monserrat S, Marcos M, Amores A, Fine I (2013) Atmospheric processes responsible for generation of the 2008 Boothbay meteotsunami. Nat Hazards. doi:10.1007/s11069-013-0811-y
Acknowledgments
We thank the New Jersey Board of Public Utilities for the funding used to purchase the 13-MHz radars. This material is based on the work supported by the US Department of Homeland Security under Award No. 2008-ST-061-ML0001. The views and conclusions contained in this document are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of the US Department of Homeland Security. This work was partially funded by NOAA Award Number NA11NOS0120038 “Toward a Comprehensive Mid-Atlantic Regional Association Coastal Ocean Observing System (MARACOOS)”. Sponsor: National Ocean Service (NOS), National Oceanic and Atmospheric Administration (NOAA) NOAA-NOS-IOOS-2011-2002515/CFDA: 11.012, Integrated Ocean Observing System Topic Area 1: Continued Development of Regional Coastal Ocean Observing Systems.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Lipa, B., Parikh, H., Barrick, D. et al. High-frequency radar observations of the June 2013 US East Coast meteotsunami. Nat Hazards 74, 109–122 (2014). https://doi.org/10.1007/s11069-013-0992-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-013-0992-4