1 Introduction

Since European settlement, Australia has a long history of destructive fires, particularly in the inhabited forest and grasslands of the southern states. Some of the most destructive fires of Australia recorded include Black Friday (1939), Dwellingup (1961), Hobart (1967), Western District (1977), Ash Wednesday (1983), Como/Jannali (1994), Canberra (2003) and, more recently, Black Saturday (2009). These fires impacted communities for many reasons described in a number of inquiries and commissions, the latest being the Royal Commission established to investigate the Black Saturday bushfires (see Teague et al. 2010). These fires were destructive in nature because of the catastrophic losses incurred to communities through the loss of human life, property, assets and infrastructure. Underpinning all of these events are particular weather conditions, fuel type and fuel condition, and how the fire impacts the community, as well as the vulnerability and response of communities.

The way in which destructive and other fires evolve and behave has, in some cases, been well researched and documented in the literature. At the forefront of the research into fire behaviour was the work conducted by McArthur (1962, 1966, 1967) in the 1950s and 1960s on grasslands and forests of southern Australia and simultaneously by Peet (1965, 1967) on forests in Western Australia. More recently, improvements in models relating to fire behaviour have been made for grasslands by Cheney et al. (1993,1998) and for dry eucalypt forests by Gould et al. (2007a, b) as part of Project Vesta that aimed to comprehensively understand and model bushfire behaviour in eucalypt forests in Australia.

Fire danger rating systems (FDRS) are used to assess the potential for bushfire occurrence, fire spread and difficulty of suppression (McArthur 1967; Sharples et al. 2009). Although many examples of fire danger ratings systems exist internationally, this paper focuses on the McArthur fire danger metres because they are widely used in southern Australia for declaring fire bans, informing people of the emerging risk of fire and for planning and allocating resources (McArthur 1966; Luke and McArthur 1978). The McArthur forest and grass FDRS are based on forest and grass fire danger indices (FFDI and GFDI, respectively), which were developed in the 1950s and 1960s using available science, case study evidence and expert opinion (Luke and McArthur 1978). The FFDI and GFDI are proportional to the predicted rate of spread of a fire on flat ground in standard fuel and so are linked to the McArthur fire spread predictions.

The Fire Danger Indices (FDIs) are non-linear functions of simple weather and drought variables that include temperature, relative humidity, wind speed and either drought factor (DF) for forests or curing for grasslands. The forest and grassland fire danger ratings (FFDR and GFDR) are categorical ratings determined from non-linearly increasing ranges of the FFDI and GFDI. Although the McArthur FDRS has been in use for over 50 years, there are some weaknesses in the underlying system. Firstly, experimental studies largely focused on many small scale fires in dry and wet sclerophyll forests in New South Wales and the Australian Capital Territory (ACT) under moderate weather conditions and on a number of experimental fires conducted in dry open sclerophyll jarrah forest in Western Australia (McArthur 1962), but the data were not published (Cheney et al. 1998). These experimental fires were supplemented with observations on three well-documented large wildfires (McArthur 1962) and field observations of small wildfires. Secondly, the most severe conditions represented by both forest and grass metres (FFDI and GFDI values of 100) were based on known worst case fires, the 1939 Black Friday for forests (Cheney et al. 1990) and the 1952 Mangoplah for grasslands. Weather conditions for these fires have since been exceeded a number of times (e.g. Ash Wednesday 1983, Black Saturday 2009). These two weaknesses limit the applicability of the McArthur FDRS in situations where the conditions may be out of the range of those in the fire danger metres. A third problem arises when relating fire danger to community losses because fire danger is determined over broad regional areas, and so factors that affect fire behaviour such as topography, atmospheric conditions and fuel hazard are not included in the FDRS. Finally, FDRS are designed to assess the potential for bushfire occurrence, fire spread and difficulty of suppression (McArthur 1967; Sharples et al. 2009) and not designed for determining the impact on communities.

While the McArthur FDRS has been an essential component of fire danger warnings in Australia, a fire danger rating system is needed that transparently reflects how fire behaviour characteristics determine not only difficulty of suppression, but also the potential for damage to a community. This topic is of fundamental importance for disaster prevention programmes, but has not received much attention in Australia. In establishing such a programme, it is critical to predict the scale of damage caused by the bushfire of a given severity. Although researchers have attempted to address this problem for earthquakes (Samardjieva and Badal 2002) and hurricanes (Pielke et al. 2008), no such study exists for the case of bushfires. Many natural hazards have a scale or rating that can be directly related to the destructive force or potential power of the hazard. For example, earthquakes use the open ended Richter scale, which is based on the amount of seismic energy released by the earthquake (USGS 2010). Additionally, a Mercalli rating was created to measure or rate the effects of an earthquake (USGS 2011) on the Earth’s surface, humans, objects and structures. For hurricanes, the Saffir Simpson Hurricane Wind Scale is used. This scale is made up of five categories distinguished by the intensities of their sustained winds and is primarily used for measuring the potential damage upon landfall (NOAA 2010). Both of these increase by orders of magnitude in impact from one level to another and are potentially linked to the amount of damage caused by the hazard (Simpson and Riehl 1981). In order to establish a link between the scale of the disaster and the amount of damage, a number of studies have attempted to find an empirical relationship between the magnitude of the hazard and the extent of damage to human life and infrastructure by investigating case studies of past hazards (Mizutani 1984; Samardjieva and Oike 1992; Samardjieva and Badal 2002; Pielke et al. 2008; Jaiswal et al. 2010). While these rating systems are measures during or after an event (not a forecast of conditions prior to one eventuating), methods of linking the destructive force to the amount of damage should be considered for categorising bushfire events. A scale that refers to the impact of a bushfire is logical for consistently assessing each event. Such information would be important for disaster prevention and risk reduction purposes in managing and preparing for future bushfires. It is also essential for any future attempts to create or improve the fire danger rating scale in Australia.

The proposal of linking loss and a fire strength metric is not a new idea. Recently, Blanchi et al. (2010) demonstrated that a relationship between fire weather severity and house loss does exist. Furthermore, Gill (1998) theorised developing a ‘Richter-like’ scale for fires based on fireline intensity as the variable associated with destructive force and loss, and other studies have suggested a link between fireline intensity and community loss (e.g. Middelmann 2007; Wang 2006). Fireline intensity is defined as the rate of heat released per unit length of fire front (Byram 1959). Because fire intensity represents an important characteristic for fire propagation, it provides critical information on fire suppression, ecological damage and fire planning (Salazar and Bradshaw 1986). Byram’s fireline intensity is often presented as the only measure of fire intensity (Chandler et al. 1983; Johnson and Miyanishi 2001), but this fails to acknowledge that other measures of energy release from bushfires may provide a better metric for fire impact. For example, losses in communities are typically caused by a combination of wind- and plume-driven fires, which is not reflected in Byram’s fireline intensity. An alternative approach to better capture the plume convective energy is to measure the rate of energy release around the fire perimeter. This presents a surrogate to describe the potential energy that could drive convective plume-driven fires and their consequent impact on communities. The energy release rate in this paper is known as Power—this is not to be confused with Byram’s use of ‘power’ which is ‘the rate at which buoyant air does work in ascending unit vertical distance of the convection column’ (Nelson 2003). ‘Power’ is used in the combustion science sense, where power is the energy released from combustion per unit time (Drysdale 1999) and not in a physics sense, where power is the rate at which work is performed for a given unit of time (Semat and Baumel 1974).

While relationships between fire strength and community impacts have been hypothesised to exist, no data have previously been compiled and analysed to support this theory. However, with a growing, and increasingly improving database of fire statistics covering Australia’s long history of destructive fires, a review of current fire danger ratings can now be conducted using the latest observations and estimates of fire behaviour and fire weather, and an investigation can be made of how these relate to community losses. Therefore, in this study, a comprehensive spatial database of forest and grass fires in Australia has been assembled, which includes fire danger indices (FFDI and GFDI), measures of fire severity (Byram’s fireline intensity and fire power), fire behaviour characteristics (e.g. rate of spread, fire area), community loss (number of fatalities, houses destroyed and economic cost of the fire), site information (e.g. vegetation type and fuel loading) and ancillary information such as weather characteristics. Such a database that combines vital information is necessary to investigate options to develop a bushfire severity scale so that better fire management processes, including community information and warnings, can be put in place.

The aim of this paper is to develop a measure of fire severity, or potential destructive force, focused on community impact, either by improving current FDRS (by accounting for fuel and slope variability), or as a standalone scale. Therefore, a new methodology was established to assess how various measures of fire severity impact on community loss. The paper summarises the procedures developed and explores the relationship between fire behaviour indices/measures of fire power and community loss.

2 Study area

South-eastern Australia experiences relatively frequent major fires with the bushfire danger becoming serious in some parts of Victoria every two to three years (Luke and McArthur 1978). This is because of the regular occurrence of extreme weather (Long 2006), the steep topography and the accumulation of flammable vegetation as well as occasional severe droughts (all of which influence fire behaviour). Eucalypts are the dominant forest type (McArthur 1967), but there are a range of other flammable vegetation types such as mallee heath and coastal heathland (Billing 1987). Due to the natural climate variability in Australia, and specifically in Victoria, large areas are prone to bushfires. Long periods of hot weather, coupled with low rainfall affect vegetation dryness and often cause drought and tinder conditions throughout the state (Bureau of Meteorology 2009). Additionally, if these drought conditions are preceded by high spring rains, the summer bushfires in more grassy communities can be intense due to high grass curing and additional fuel load on the surface (Bureau of Meteorology 2009).

3 Data and methods

To assess the relationship between loss and the destructive power of the fires studied, several data sets were required. Fire weather, fire behaviour, vegetation type, fuel loading, topography, community loss and house and population density information were collected for each fire. The data sets were compiled from a range of sources and each data set is discussed separately. The spatial layers and the tabular data were linked spatially so that where possible spatial information could be extracted for analysis. Several fires were included for which no community loss was recorded so that the risk of loss could be assessed for given weather conditions.

3.1 Summary of fires in the southern states of Australia

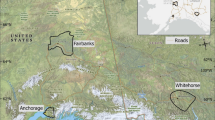
A total of 79 fires were analysed in this study. The number of fires included was largely restricted by data availability. Most of the fires were in Victoria (72); one in Western Australia, two in South Australia, two in New South Wales and two in the ACT. Of the 79 fires, 47 of these were in forested regions and 32 were in grass. Of the fires studied, 35 had one or more fatalities during the event, 25 of these fires occurred in forest and 10 in grass. In terms of house loss, 57 of the 75 fires with house loss information had one or more houses destroyed, 34 of these being in forest and 23 in grass. The locations of the bushfires analysed in this paper are shown in Fig. 1.

Fig. 1
figure 1

The locations of the major bushfires analysed in this study

Full size image

3.2 Fire perimeters and fire behaviour mapping

A Victorian fire history database created by the Country Fire Authority (CFA) and the Department of Sustainability and Environment (DSE) containing a digital perimeter for many fires was used; however, for some older fires (pre-1980s) and fires from other states, perimeters were only available as paper maps so they were scanned, digitised, geometrically rectified and then added to the geographical information systems (GIS) spatial database.

Many of the fires occurred over several days or were several fires that eventually coalesced. Where it was known, the fire perimeter on the day the damage was incurred was used in the analysis. Isochrones, or the locations of the fire perimeter at known times, were obtained where possible for each fire. These contours detail the spatial spread of the fire perimeter over temporal scales ranging from 10 minutes to daily intervals. Such detailed information is essential for understanding how the fire propagated pre- and post-frontal change, as well as quantifying the rate of spread at various points across the fire. The level of detail for each fire varied depending on the source and age of the fire, and unfortunately, very few fires had highly detailed isochrone information (such as those available for the 2009 fires).

3.3 Fire weather variables

Weather variables were obtained from the Bureau of Meteorology’s automatic weather station data and government reports that described data from manual and automatic weather stations. These data included temperature, relative humidity, rainfall and wind speed and direction. Often the weather stations were a long distance from where the fire occurred and the conditions (topography/elevation) may have been very different. Therefore, the distance between the fire and the weather station was calculated so that this could be incorporated into the analysis.

3.4 Slope

Slope data were calculated from the VicMap DEM20 (resolution of 20 m) for Victorian fires and GEODATA 9 Second digital elevation model (DEM-9S) version 3 (www.ga.gov.au/meta/ANZCW0703011541.html) (resolution approximately 250 m) for all other states.

3.5 Fuel types and loads

Best estimates of fuel load were taken from the literature (including case study reports, journal articles and government agency documents), although some areas lacked any estimate, so modelled fuel loads were used. Modelled fuel loads were created using fuel types, fire history and accumulation curves. Information about the grouping of fuel types and the fuel accumulation rates can be found in Tolhurst (2005) and McCarthy et al. (2009). These data were used to produce estimates of the bark load, surface load and elevated load. For consistency with the literature data, only surface fuel loads estimates from the modelled data were incorporated into the analysis. Where there were no estimates for fuel load in the literature or modelled data, estimates were taken from Gellie et al. (2011).

3.6 Community loss and density

Community loss data were collected from a range of sources many of which were already compiled by the CFA. Estimates of economic loss were also used in the analyses. For the Victorian fires in this study that occurred between 1939 and 2008, economic figures were acquired from the CFA and DSE. These data were constructed according to the State Emergency Risk Assessment Methodology (State Emergency Mitigation Committee 2005) and were corrected to 2008 Australian dollars. Economic data for the 2009 fires were acquired from a recent economic loss assessment (Stephenson 2011), which is based on methods developed by the OESC (2008). These economic figures were also converted to 2008 Australian dollars. This framework was also used to calculate simple economic costs for fires other than those in Victoria.

To assess the community loss in relation to the community affected, house and population density information were required. In order to be more representative in describing the impact of house loss, fatalities and economic loss in fire-affected communities, average densities were calculated over the fire-affected area only. For house density, where possible, aerial photography obtained over a fire-affected region around the time of the fire was collected. These images were georectified, collated as a mosaic, and then each property was digitised to establish the housing density.

Aerial photography was not available for all regions and was not always feasible for ascertaining house density and for estimating the population density; consequently, Australian Bureau of Statistics (ABS) population and housing census data were incorporated. This was achieved by using statistical local boundaries, local government or census districts to provide the best available estimate of broad population and housing densities using the proportion of area burnt and proximity to towns. The ABS data set at the closest time to the fire event was used.

A comparison of the orthophoto and ABS data method was conducted for the 2009 fires to assess how well the two methods compared in capturing housing density. This analysis showed that in the 2009 case, the ABS method overestimated housing density, and for this reason, we weighted the different methods, giving lower weighting to the ABS data (see Table 1).

Table 1 Data accuracy classification system
Full size table

3.7 Fire danger indices

McArthur’s FDIs were calculated using the weather data from Bureau of Meteorology and government reports. The data were taken when the FFDI was highest for the day. To test the applicability of McArthur’s fire danger metre on community loss, FFDI (Mk V) and GFDI (Mk IV) were calculated for each fire using the same methods as used by the Bureau of Meteorology (2006).

Both FFDI and GFDI are functions of temperature, humidity and wind speed at a height of 10 m. The GFDI includes a measure of grassland curing, whereas the FFDI includes a measure of ‘fuel availability’ reflected in the DF, which is a measure of long-term drying. The DF is a function of the Keetch–Byram Drought Index (KBDI), which estimates the cumulative moisture deficiency in the upper soil layers, and it also incorporates information about the rainfall record (Keetch and Byram 1968). Equations used to determine FFDI were those given in Noble et al. (1980), but with the equation to determine the DF replaced by Griffiths’ algorithm (Griffiths 1999). The equation to determine the GFDI was that given in Purton (1982). Because the indices are used for broad scale applications, both forms of the indices assume standard fuel loadings, being 4.5 t/ha for grasslands (Luke and McArthur 1978) and 12.5 t/ha for forests (McArthur 1967).

3.8 Adjusted fire danger indices

Slope and fuel loading/structure affect fire behaviour (Luke and McArthur 1978). However, these factors are not included in the McArthur FDIs. To better reflect the fire behaviour over the fire area, FFDI and GFDI were adjusted to account for fuel loading and slope in a way that reflects the Mark V Forest Meter and Mark V Grassland Meter spread rate predictions. Equations 1 and 2 are the fuel-adjusted FFDI and GFDI (FFDIF and GFDIF, respectively)

$$ {\text{FFDIF}} = {\text{FFDI}} \times w/1.25, $$
(1)
$$ {\text{GFDIF}} = {\text{GFDI}} \times w/0.45, $$
(2)

where w is the average fuel load over the fire area in kg/m2, 1.25 is the standard fuel loading for the FFDI (12.5 t/ha) converted to kg/m2, and 0.45 is the standard fuel loading for the GFDI (4.5 t/ha) converted to kg/m2. Equations 3 and 4 are the slope-adjusted FFDI and GFDI (FFDIS and GFDIS, respectively)

$$ {\text{FFDIS}} = {\text{FFDI}} \times \exp (0.069\theta ), $$
(3)
$$ {\text{GFDIS}} = {\text{GFDI}} \times \exp (0.069\theta ), $$
(4)

where θ is the average slope encountered by the head fire in degrees. The multiplier exp (0.069θ) is given in Noble et al. (1980) as an approximation to the increase in no-slope rate of spread in the Mark V Forest Meter when the slope angle is θ degrees. Adjustments for both fuel and slope are given by Eqs. 5 and 6

$$ {\text{FFDIFS}} = {\text{FFDI}} \times \left( {\frac{w}{1.25}} \right) \times \exp (0.069\theta ), $$
(5)
$$ {\text{GFDIFS}} = {\text{GFDI}} \times \left( {\frac{w}{0.45}} \right) \times \exp (0.069\theta ), $$
(6)

These adjustments were used as predictor variables for community loss to see whether they would be better predictors than the unadjusted FFDI or GFDI.

3.9 Intensity and power measures

The most commonly used measure of the ‘strength’ of a fire is Byram’s fireline intensity, I B , which is the rate of heat release per unit length of the active fire front (Byram 1959). It is calculated as

$$ I_{B} = hw_{a} R, $$
(7)

where w a (kg/m2) is the fuel available for burning in the fire front, h (kJ/kg) is the heat yield of the available fuel, and R is the forward rate of spread (m/s). Fireline intensity is thus the rate of energy release over the depth of flame behind unit length of the fire front.

To create a measure describing the energy release rate, two methods were considered. The first method was to multiply the energy release rate per unit length by some characteristic fireline length for which the intensity is reasonably large. This gives an estimate of the power of the fire, PWR1, in the form

$$ {\text{PWR}}1 \, = \, {\rm I}_{\rm B} \times \alpha P, $$
(8)

where P is the perimeter of the fire, and α is the characteristic fireline length. Three values of α were used, which were equal to the fraction of the ellipse perimeter at which the intensity drops to 0.75, 0.5, and 0.25, respectively, of the maximum intensity, each of which can be shown to be dependent on length-to-breadth ratio, LB. Regressions of log(α) on functions of LB gave

$$ \alpha = \left\{ {\begin{array}{*{20}c} {\exp (1.285 - 1.422 \sqrt {LB} )} \hfill & {I_{B} > 0.25I_{B\max } } \hfill \\ {\exp (4.779 - 5.281 \, LB^{0.25} )} \hfill & {I_{B} > 0.50I_{B\max } } \hfill \\ {\exp (1.472 - 2.558 \sqrt {LB} )} \hfill & {I_{B} > 0.75I_{B\max } } \hfill \\ \end{array} } \right. , $$
(9)

with minimum R 2 of 0.98. The resulting variables are denoted as PWR1(0.25), PWR1(0.50) and PWR1(0.75).

Catchpole et al. (1982) extended the definition of intensity in Eq. 7 to intensity around the perimeter of a fire, where R is replaced by the rate of spread normal to the perimeter. The spread rate, and thus the intensity, varies around the perimeter, as discussed in Catchpole et al. (1982). An estimate of the power of the fire, PWR2, is given by integrating the intensity around the fire perimeter, which is shown in Catchpole et al. (1982) to be

$$ {\text{PWR}}2 = \int {I_{B} {\text{d}}s = hw_{a} \frac{{{\text{d}}A}}{{{\text{d}}T}}} { }, $$
(10)

where dA/dT is the rate of area growth with time. It is shown in Harris et al. (2011) that for an elliptical fire with length D T , length-to-breadth ratio LB, at a time T after ignition.

$$ {\text{PWR2}} = \frac{{\pi hw_{a} }}{{2{\text{LB}}}}\frac{{D_{T}^{2} }}{T} { }, $$
(11)

Note that this assumes that the heat yield and available fuel remain constant around the fire, whereas recent studies (e.g. Linn and Cunningham 2005) suggest that the combustion processes are different for heading, flanking and backing fires, thus h and w a would vary somewhat around the perimeter.

The use of the whole fire was necessary as the position of losses for older fires was unknown. However, as stated in Wade and Ward (1973), fires are a function of fire size and the rate at which they spread since this drives the convective phases of the fire. This process draws energy from all sides of the fire perimeter. Having a better account of fire intensity along the total fire perimeter and therefore the total energy output better describes the potential of increased convective energy.

To calculate the power of the fire for fires that have a ‘blow-out’ due to a wind change, a number of different equations are required. Blow-outs in this study are defined as the rapid spread of fire following a major wind change when the flank turns into the head fire. The methods used to calculate the power of the fire from these blow-outs can be found in the Appendix of Harris et al. (2011). The equations are just variations on the equation for an ellipse and cover square, rectangular and triangular blow-outs. This is explained further in the next section.

3.10 Extracting data for calculating power and intensity

To calculate PWR1 and PWR2, each fire was divided into sections that are described by fitting the best geometric shape (e.g. ellipse to represent the main run of the fire). For these geometric shapes, the fire length and width were measured in a GIS platform, and the corresponding length-to-breadth ratio and fire area were calculated (Fig. 2). While each fire does not follow a precise shape, this method was the most consistent and efficient at encapsulating and representing each fire event. Fire start and end times of the ellipse and blow-out were also necessary to calculate the rate of spread (R) of each part of the fire.

Fig. 2
figure 2

One example of applying shapes to actual fire events, in this case the Murrindindi fire: B is breadth of ellipse, L is length of ellipse, B B is the breadth of the blow-out (in this case a rectangle), and L B is the length of the blow-out

Full size image

The average fine fuel load (w) was extracted from either the literature or the modelled data for the fire-affected area and assumed to equal the available fuel. For the heat yield (h), 20,000 kJ/kg is regarded as a reasonable average for the range of fuels commonly consumed by bushfires (Luke and McArthur 1978). Following Nelson and Adkins (1986), this was corrected for a nominal 20 % energy loss due to radiation and a nominal 5 % loss due to the evaporation of moisture (assuming a moisture content of 5 %) from Table 3.2 in Byram (1959). The power and intensity values were then calculated using the various dimension measurements, rate of spread, fuel load estimates and heat yield. Finally, the average slope was calculated by taking the mean slope within the fire perimeter in a GIS. Average values over the fire were used because the position of the losses was largely unknown. For the power variables, the total power from ellipse and blow-out was used. However, for fires with triangular blow-outs, PWR1 was not applicable, as a characteristic distance for a triangular blow-out is hard to determine. For rate of spread and intensity, the maximum ROS and IB over the ellipse and blow-out were used to be consistent with using the highest FDI values. As PWR1 could not be calculated for triangular blow-outs, only data with PWR1 values were used for comparison of variables.

3.11 Data accuracy classification system

The data were classified into categories that represented the reliability and uncertainties of the data used in the analysis (Table 1). These classifications were based on previous studies such as Cheney et al. (1998) and Bushfire CRC (2009). The numerical weights associated with each category were estimates of the relative reliability determined when setting up the database. These weights were used in the statistical analysis of the relationships, as described in the statistical methods section.

3.12 Statistical methods

The aim was to establish whether there was a relationship between any of the FDIs (raw or adjusted) or any of the measures of the strength of the fire (the independent variable x) and community loss (the dependent variable Y), and if so, which measure of strength (or FDI) gave the strongest relationship.

The data were analysed using generalised linear models (McCullagh and Nelder 1989). To deal with the overly large variation (overdispersion) often found in count data, a quasi-Poisson was assumed. Another possible model that can cope with overdispersion is the negative binomial model, but as pointed out by Ver Hoef and Boveng (2007), the quasi-Poisson model gives more weight to larger losses. Since it is critical to model high losses accurately, the quasi-Poisson model was considered to be preferable.

In addition to overly large variation, count data may contain more zeros than would be allowed for by the standard distributions, and there is also a possibility of underrepresentation of zeros because of the bias towards including fires with some losses in the database. To deal with these situations, a hurdle model (Mullahy 1986; Zeileis et al. 2008) was used. In the hurdle model, there are two component models: a truncated count model that is used for the positive counts and a hurdle component that models zero versus positive counts. In the case of fatalities, for example, the hurdle model may be interpreted as there being one process that determines whether there was a fatality on a fire and another process that determines how many fatalities there were, given that there was at least one fatality.

For the count model with two regressor variables x 1 and x 2, the regression equation with a log link is

$$ \log (\mu ) = \eta = b_{0} + b_{1} x_{1} + b_{2} x_{2} , $$
(12)

where μ is the conditional mean of Y, and b 0, b 1 and b 2 are regression coefficients. A binomial model was used for the zero-hurdle component. For two regression variables, this is

$$ \log [\pi /(1 - \pi )] = \eta^{*} = c_{0} + c_{1} x_{1} + c_{2} x_{2} , $$
(13)

where π is the probability of a non-zero loss, and c 0, c 1, and c 2 are regression coefficients. For the hurdle model with log link, the mean regression relationship is given by

$$ \log (M) = \eta + \log (1 - f_{z} (0,\pi )) - \log (1 - f_{c} (0,\mu )), $$
(14)

where Μ is the mean loss, η is the function of the regression coefficients in Eq. 12, f z (0,π) is the probability of no losses in the zero-hurdle model, and f z (0, μ) is the probability of no losses in the positive count model. For example, in the case of the hurdle model with a Poisson positive count model and a binomial zero-hurdle model, f z (0, π) = (1−π) and f z (0, μ) = exp(−μ). Equation 14 is used to predict mean loss.

The software did not allow a quasi-Poisson hurdle model. However, the estimates of the coefficients from the quasi-Poisson model are the same as those for the Poisson model, but the standard errors are larger (Agresti 2002). Thus, the hurdle Poisson model was used to fit the data, and the standard errors were calculated using the sandwich covariance matrix estimator (White 1994), to test for the significance of the coefficients. The models were fitted using the software R (R Development Core Team 2011) with the extra packages pscl (Jackman 2011), lmtest (Zeileis and Hothorn 2002) and sandwich (Zeileis 2004, 2006) included for analysis of the hurdle model and for the sandwich covariance estimator.

The economic loss data were continuous and highly skewed to the right. One method of analysing this type of data is to use a generalised linear model with a Gaussian distribution and a log link which essentially assumes a Gaussian distribution of the logarithm of the data. On the other hand, economic loss is highly correlated with house loss and fatalities. As an approximation, the economic loss was rounded to the nearest million dollars and hurdle Poisson models were fitted, as the Gaussian model gave poor regression diagnostics.

The models were assessed using three goodness of fit statistics: the root mean squared error (RMSE), the mean bias error (MBE) (Willmott 1982), and for a non-dimensional standardised measure of goodness of fit, the correlation, r, between the observed values and the fitted model predictions, as recommended by Agresti (2002).

Untransformed regressor variables were fitted as this provided better error statistics than using a logarithmic transformation. The logarithm of house or population exposure (fire area multiplied by density) was used as a covariate regressor variable depending on whether the independent variable was house loss, fatalities or economic loss. For comparison of models, the regressions were unweighted (apart for economic loss that had different reliabilities in the Y variable), but in the final model development, the regressions were weighted. The weighting was done using the product of the relevant fuel, fire behaviour and density weights (as given in Table 1) as this was presumed to reflect the way the errors compounded in the variables. If spread rate was estimated from the McArthur equations, or if one of the FDIs (raw or adjusted) was the regressor variable, the weather reliability weighting was included in the weighting. Sensitivity to the weighting was examined by fitting a non-weighted model and comparing the results.

The analyses were supplemented by residual plots: residuals against fitted values, normal quantile plots of the standardised deviance residuals, square root standardised deviance residuals against fitted values and standardised Pearson residuals against leverage (see Davison and Snell (1991) for details).

4 Results: statistical relationship between loss and fire-related variables

4.1 House loss

Table 2 shows the results of fitting hurdle Poisson models using each fire behaviour measure in turn as the independent variable. The fuel-adjusted FFDI and GFDI were better than the unadjusted values, but the slope-adjusted FDIs were worse. The best predictors were FFDI, GFDI, IB, PWR1(0.50), PWR1(0.75) and PWR2. Of these, the performance of PWR1(0.75) was marginally the best. PWR1 improved with increasing α (smaller fraction of the perimeter) and was better than PWR2 for α > 0.25. ROS was a relatively poor predictor.

Table 2 Correlation (r), RMSE and MBE between observed and predicted values for models predicting house loss from house exposure and fire-related variables (unweighted)
Full size table

In the following analyses for house loss, the best models for the combined data set are developed using weighted data, as appropriate, and the terms in the zero-hurdle model are tested for significance.

4.1.1 Using PWR1(α = 0.75) as the predictor variable

A hurdle Poisson model was fitted using PWR1(0.75) as the predictor variable. The positive count component of the hurdle model was of the form

$$ \eta_{H} = b_{0} + b_{1} {\text{PWR}}1(0.75) + b_{2} \log ({\text{HEXP}}), $$
(15)

where the subscript Η indicates house loss, HEXP is the house exposure (fire area times house density), and b 0, b 1 and b 2 are regression coefficients. Note that to predict the mean number of houses lost, Μ H , it is necessary to add the hurdle component to the right hand side of Eq. 15 as in Eq. 14. Only the covariate was significant in the zero-hurdle model. All coefficients in the positive count part of the hurdle model were significant (using a sandwich test for the Poisson model). The predicted values are plotted against the observed values in Fig. 3.

Fig. 3
figure 3

Predicted values plotted against observed values for the prediction equation for house loss in terms of PWR1(0.75) and HEXP (Eq. 15). Fire reliability is shown by shading in the symbols: black filled circles weight greater or equal to 0.55, grey filled circles weight less than 0.55 and greater or equal to 0.35, and open circles weight less than 0.35

Full size image

The goodness of fit statistics (and for the models developed for fatalities and economic loss) are given in Table 3, and the regression coefficients (and their standard errors) are given in Table 4 (V is the fire-related variable considered and CV is the risk covariate used).

Table 3 Goodness of fit statistics for the fitted regression models in Eqs. 15, 16, 17 and 18
Full size table
Table 4 Coefficients and standard errors for fitted regression models in Eqs. 15, 16, 17, and 18. Standard errors are given in parenthesis. Standard errors for the hurdle Poisson count model are sandwich standard errors. V is the fire-related variable considered and CV is the risk covariate used
Full size table

4.1.2 Effect of weighting

The effect of weighting was examined on the house loss model in Eq. 15 by comparing the weighting used with equal weighting. The change had only a small effect on the resulting model coefficients. The coefficient for the intercept, for instance, changed from 1.4873 to 1.4591, a difference of about 2 %. The r values, RMSE and MAE were quite similar, but the bias was less in the unweighted model (1.9 as opposed to −7.7).

4.1.3 Using FFDIF as the predictor variable

A model was also created using FFDIF. It was used in preference to GFDIF as there are generally more house losses in forested areas. The positive count component of the hurdle model was of the form

$$ \eta_{H} = b_{0} + b_{1} {\text{FFDIF}} + b_{2} \log ({\text{HEXP}}), $$
(16)

Only the covariate was significant in the zero-hurdle part of the model. The goodness of fit statistics were similar to those of Eq. 15: r and the RMSE were slightly worse, but the MAE and the MBE were slightly better. Predicted values are plotted against the observed values in Fig. 4.

Fig. 4
figure 4

Predicted values plotted against observed values for the prediction equation for house loss in terms of FFDIF and HEXP (Eq. 16). Fire reliability is shown by shading in the symbols: black filled circles weight greater or equal to 0.55, grey filled circles weight less than 0.55 and greater or equal to 0.35, and open circles weight less than 0.35

Full size image

4.2 Fatalities

Models were fitted using each fire-related variable in turn, and the results are shown in Table 5. Again, the fuel-adjusted FFDI and GFDI were better than the unadjusted values, but the slope-adjusted FDIs were generally worse. The best predictors were FFDI, GFDI, PWR1(0.50), PWR1(0.75) and PWR2. Of these, the performance of PWR1(0.75) was the best. PWR1 improved with increasing α and was better than PWR2 for α > 0.25. ROS was a relatively poor predictor. IB was similar to the worst of the alternative formulations for PWR1. Note that the data set was dominated by three high fatality fires (Murrindindi, Kilmore and Black Friday—Central and North); thus, any model for fatalities may not be robust. A model was created using PWR1(0.75), but it should be regarded with caution.

Table 5 Correlation (r), RMSE and MBE between observed and predicted values for models predicting fatalities from population exposure and fire-related variables (unweighted)
Full size table

The fitted model was of the form

$$ \eta_{F} = b_{0} + b_{1} {\text{PWR}}1(0.75) + b_{2} \log ({\text{PEXP}}), $$
(17)

where PEXP is the population exposure. None of the hurdle model coefficients were significant so a quasi-Poisson model was used. The predicted values are plotted against the observed values in Fig. 5.

Fig. 5
figure 5

Predicted values plotted against observed values for the prediction equation for fatalities in terms of PWR1(0.75) and PEXP (Eq. 17). Fire reliability is shown by shading in the symbols: black filled circles weight greater or equal to 0.55, grey filled circles weight less than 0.55 and greater or equal to 0.35, and open circles weight less than 0.35

Full size image

4.3 Economic loss

House exposure performed slightly better than population exposure, so it was used as a covariate. Loss was also weighted by the economic reliability given in Table 1. Models were fitted using each fire variable in turn, and the results are shown in Table 6. Again, the fuel- and slope-adjusted FFDI and GFDI were better than the unadjusted values. In this case, the slope-adjusted FDIs had similar predictive power to the fuel-adjusted FDIs. The best predictors were the power variables. PWR1 improved with increasing α and was again better than PWR2 for α > 0.25. ROS and IB were relatively poor predictors. The combined data set was dominated by two economic loss fires (Murrindindi and Kilmore); thus, any model for economic loss may not be robust. A model was created using PWR1(0.75), but it should be regarded with caution.

Table 6 Correlation (r), RMSE and MBE between observed and predicted values for models predicting economic loss from house exposure and fire-related variables (unweighted)
Full size table

The positive count regression model was of the form

$$ \eta_{E} = b_{0} + b_{1} {\text{PWR}}1(0.75) + b_{2} \log ({\text{HEXP}}), $$
(18)

where the subscript Ε refers to economic loss that is measured in millions of dollars. For this model, only the intercept was significant in the zero-hurdle model. The predicted values are plotted against the observed values for this model in Fig. 6.

Fig. 6
figure 6

Predicted values plotted against observed values for the prediction equation for economic loss in terms of PWR1(0.75) and HEXP (Eq. 18). Fire reliability is shown by shading in the symbols: black filled circles weight greater or equal to 0.55, grey filled circles weight less than 0.55 and greater or equal to 0.35, and open circles weight less than 0.35

Full size image

5 Discussion

5.1 Fire characterisation and limitations

Effort was made to obtain the most reliable data for each fire, but in some cases, this was not possible. Continued development and improvement in the data quality will be made, which may alter some of the findings from this research. To add significant value and improve its use for analysis, additional bushfire case studies should be added, particularly from the national and international scene. The lack of fires from other states obviously biases the analysis as the sampling is not random. The analysis is also biased because a disproportionately small number of fires that did not cause damage are in the database. These fires would be generally smaller fires, and the bias would affect the estimation of the hurdle model parameters, in that the probability of no losses would be underestimated. In addition to this, the modelling is conditional on there being an ignition. This could be extended in future work.

The method of down-weighting poor data is crude and neither takes account of whether the error was in the dependent or independent variable nor uses an estimate of the magnitude of the error. Doing these things would complicate the analysis considerably. Future analysis should cover these aspects.

Using the independent variable (power of the fire or the adjusted FFDI) in a linear form in the equation for the logarithm of loss (such as Eq. 15) results in an exponential form of the independent variable in the prediction equation for loss. Thus, non-zero loss is predicted for zero-values of the independent variable which is obviously incorrect. The problem is exacerbated as the values of the covariate (density or exposure) are increased. However, it is not unusual to get quite high losses for small values of power when the house or population density is high or the fire area is large. As an example, the Como/Jannali fire had a low value of PWR1(0.75) of 6.7 GW but a high house density of 145 houses km−2 (median 1.57 in the data set). It had an economic loss of 51 million dollars (median 10 in the data set), and the model in Eq. 18 predicted 34 million dollars.

To develop a more thorough understanding of the impacts of fire on communities, future estimates of the power of a fire would benefit from focusing on the region of the fire that caused the damage to a community. An estimate of the power of the fire along a given isochrone could be obtained by integrating Eq. 7 in Catchpole et al. (1982) for the rate of spread (and hence intensity) of a point on an arbitrary fire front along the isochrone. Also, more complete measurements of fire behaviour could be made by improving fuel accumulation and fuel load models and by adding fuel estimates for near surface and elevated fuel components, medium woody debris, canopy and live/dead components like those modelled by Keith et al. (2010). This would better quantify the energy release rate of the fire as it considers all available fuels rather than only surface fuels. Furthermore, the vertical atmospheric structure, and how that plays a role in influencing the power of fire (Potter 2002) should be incorporated. Other methods of estimating the energy released during a fire event should also be further investigated, such as those methods developed by Wooster et al. (2005), which estimate fire radiative energy (FRE) and fire radiative power (FRP) from remotely sensed data. Finally, how the scale of a fire event alters the ability of mitigation strategies such as planned burning to alter impacts, and of communities and fire agencies to respond are also important gaps in our knowledge that need to be addressed.

5.2 Performance of the predictor variables

This paper introduced two new methodologies to estimate fire severity, or potential destructive force, through measuring the power of fire. Here, an assessment of the variables used in this paper is made, especially of how they compared and performed with respect to predicting community loss.

5.2.1 FFDI and GFDI

Generally, FFDI and GFDI were found to perform poorly in relation to community loss when compared with the adjusted values and with the measures of power. This is almost certainly due to inherent limitations of the FFDI and GFDI which are meant for broadscale application and solely rely on meteorological input data and are therefore not suitable for a range of fuel loads and topographic regions. It should also be noted that FFDI and GFDI were designed as a predictor of fire initiation, fire spread, ease of suppression and impact on forest and rural farmland values, and not for community loss.

5.2.2 FFDI and GFDI adjusted

The adjustment to the FFDI and GFDI which gave the best predictions was that for fuel alone. Adjusting for slope and fuel provided better predictions than the unadjusted indices but generally not as well as those for fuel alone. The problem may be that the adjustment for average slope over the whole fire does not capture the fire behaviour at the site of the losses. The fuel-adjusted indices were almost equal to or better than the power variables in predicting community loss.

5.2.3 Byram’s intensity and rate of spread

Byram’s fireline intensity has been shown to have great practical value as an indicator of fire severity for fire control purposes (Catchpole et al. 1982), and ecologically, the index has been used to relate damage of trees to fire severity (McArthur and Cheney 1966; Van Wagner 1973). For house loss, it was a possible contender as a predictor variable, but it was not quite as good as the best of the power variables. Rate of spread was a generally a worse predictor of loss than the fuel-adjusted FDIs, IB or the power variables.

5.2.4 Power of the fire

PWR1(0.75) was the best predictor of community loss, although FFDIF came close to it for predicting house loss. It was always slightly better than PWR2. The predictive power increased as less of the perimeter was used, but as it was better than IB that only considers unit length of the perimeter, there is obviously merit in including some characteristic length which is assumed to have burned at a reasonably high intensity.

PWR1(0.75) needs predictions of time since ignition and fire area, and the exposure covariate model needs predictions of fire area. Emerging tools such as Phoenix RapidFire, which is a research and development tool developed by the University of Melbourne and Bushfire CRC, can now be used to estimate the area and time since ignition of a fire through simulation and fire behaviour prediction models. This could be used to provide predictions of possible loss on a local area basis.

5.3 Implications for developing a bushfire severity scale

The current FDRS based on FFDI and GFDI is not adequate for predicting community loss. This report suggested simple modifications to the FFDI through incorporating slope and fuel-loading factors (especially fuel) to increase the predictive power of FFDI. Furthermore, power of fire measures, with continued improvement, could be further explored as a basis for developing a bushfire severity scale. This paper provides an initial insight into establishing a new methodology to describe fire through reconstructing the power released at certain parts of the fire. However, to fully understand and make use of this methodology as a fire severity scale, it is necessary to move from reconstruction to prediction.

The implications that this research, combined with further work, will have on policy decisions is considerable. The ability to calculate the power of the fire, and then at a local scale use it to predict the number of fatalities and house losses (within a range) will have implications for providing communities with more targeted advice to leave in advance of Code Red bushfire days and therefore may result in reducing the number of fatalities. Furthermore, these finding could have implications on fuel management such as prescribed burning for reducing fuel hazard and fuel loads therefore impacting the destructive power of the fire.

Predicting the behaviour of natural phenomena such as fire requires robust fire behaviour models. Computationally, local fire behaviour prediction is becoming more achievable through advancements such as Phoenix RapidFire, but the predictions produced are still only a function of the quality of the data and models that underpin them. This research highlighted the importance of this knowledge in informing fire agencies and community decision-making. Such knowledge is especially important when events of unprecedented scale and magnitude occur. Additionally, events such as those on Black Saturday will invariably occur in a warming and drying climate (Lucas et al. 2007), and making predictions about what might happen involves considerable uncertainty. This uncertainty can be reduced if a solid scientific base can be built that captures what is known from past events (which is not currently the case), and a contemporary view and understanding of fire, how it behaves, how it can be described, and how it can impact communities are therefore needed.

The paper highlights the need for further research into a contemporary fire danger rating system that not only meets traditional fire agency needs relating to preparedness decision-making and impact of forest and rural values, but also includes the potential for bushfires to impact communities. It shows that physical measures that relate to community impact exist and are an improvement on existing FDIs and the standard Byram’s fireline intensity. It also confirms that bushfire behaviour (rate of spread, fire shape and size, fuel consumption and power) and community (settlement patterns) attributes affect bushfire risk and that improved science and data will improve fire danger rating and risk assessments.

6 Conclusion

Developing more robust theories and models of fire behaviour and the impacts of fire on communities is critical for current and future fire risk management. To date, much of Australia’s fire history had not been collated and considered in an integrated way, and yet, this information provides an insight in to the nature and intensity of fires that result in the loss of life and assets or have the potential to do so. This study compiled the most comprehensive database of observations and estimates on fires that have occurred in Victoria and elsewhere in Australia available today. While vast improvements could be made to both the data analysed and the measurements of power of fire, results from the statistical analysis suggest that the current FDRS could be adjusted to improve the warning system, so it better relates to community loss. However, a better approach would be to continue exploring how to measure the power of fire and begin investigating how to base a new bushfire threat warning system on these measures. Given the importance of accurately predicting bushfire threats, improving the measures and predictability of fire power should be a priority in bushfire research in Australia.