1 Introduction

The concept of risk has been introduced in natural hazard management since the experiences from past years suggested that elements at riskFootnote 1 and vulnerability should be increasingly considered within this framework in order to reduce losses (e.g. International Standards Organisation 2009; Commission of the European Communities 2010). Major losses in the European Alps are associated with torrent events (Oberndorfer et al. 2007; Hübl et al. 2011). The term torrent refers to steep rivers within a mountainous environment. Torrents are defined as constantly or temporarily flowing watercourses with strongly changing perennial or intermittent discharge and flow conditions (Aulitzky 1980; ONR 2009), originating within small catchment areas (Slaymaker 1988). Torrent events are a main challenge for society in Austria. On a regional scale, these events are concentrated in the western part of Austria where considerable differences in elevation shape steep watersheds. At the outlet of these watersheds, large torrent fans are developed, which are used for settlement purpose since the beginning of the historical colonisation and commodification of Alpine valleys.

In Austria, a database of destructive torrent events was established and analysed concerning monetary losses (Oberndorfer et al. 2007). A total number of 4,894 damaging torrent events were reported between 1972 and 2004, and for almost 4,300 events, the process type could be determined ex post due to available event documentation. Process types included debris flows (28.7%), hyperconcentrated flows (49.2%), flooding with bedload transport (21.8%), and floods (0.3%). Annual losses due to torrent events amounted to around €25 million, while an average direct loss per event due to these 4,300 records amounted to approximately €170,000 (in 2010 values). Approximately one-third of the losses could be ascribed to infrastructure facilities, and two-third to buildings (Fuchs 2009). Within the period under investigation, 49 people died and 21 people were physically harmed. The annual distribution of the losses showed that considerable cumulative damage exceeding €1 million per event occurred in 1975, 1978, and 1991. In contrast, in 1976 and 1984, the average damage per event summed up to €11,000 and €16,000, respectively. A considerable number of events were reported from 1974, 1990, and 2002, leading to the conclusion that a high number of events do not necessarily result in high losses, and vice versa (Oberndorfer et al. 2007). An additional analysis of destructive torrent events between 1950 and 2009, derived from a reanalysis of written reports that were compiled during the implementation of hazard maps by the Austrian Torrent and Avalanche Control Service, has shown a decreasing trend related to the overall number (N = 11,185, annual mean = 186, Totschnig et al. 2011).

In European mountain regions, the concept of risk has proven as a valuable instrument to reduce the susceptibility of buildings and infrastructure to natural hazards (e.g. Fuchs et al. 2004; Kienholz et al. 2004; Zischg et al. 2005a) and thus to reduce losses. Based on this concept, tailored strategies for sustainable use of mountain areas for settlement, economic purpose and recreation can be developed (Holub and Fuchs 2009). Risk is defined as a measure of the probability and severity of an adverse effect to the society (Fell et al. 2008) and is quantified by a function of probability of a phenomenon of a given magnitude times the consequences. However, in practice, the concept of risk is regularly applied taking a static viewpoint (Fuchs et al. 2004), while losses are the predictable result of interactions among three major dynamic systems (Mileti 1999): the physical environment, which includes hazardous events; the social and demographic characteristics of the communities that experience them; and the elements at risk such as buildings, roads, and other components of the built environment.

Even if research on the hazardous events has a long tradition, above all in engineering sciences and with respect to mountain hazards (e.g. Eckel 1958; Schuster and Turner 1996; Glade et al. 2005; Fell et al. 2008), there is a lack of studies related to the spatio-temporal development of risk (Fuchs et al. 2008; Fuchs and Keiler 2008) and the underlying vulnerability of values at risk and of communities (Fuchs 2009; Papathoma-Köhle et al. 2011): Recently, these shortcomings have been addressed focusing either on process dynamics (e.g. Keiler et al. 2010 with respect to climate change or Fuchs et al. 2007b) with respect to the implementation of technical mitigation measures) or on dynamics of elements at risk exposed (Fuchs et al. 2005; Keiler et al. 2005, 2006a; Zischg et al. 2005b). However, until now, there is a particular gap on the spatial dimension of vulnerability: Space is—apart from time—a key factor when vulnerability is assessed, since vulnerability only emerges due to the physical overlap between hazardous events and elements at risk, and due to the spatial synchrony of such events and the exposure of elements at risk—which is a positivist approach rooted in the conceptualisation of risk common in the natural sciences and engineering (Fuchs and Keiler 2012).

Within the concept of risk, vulnerability is a key variable when addressing potential future dynamics resulting from mountain hazards. Vulnerability is defined by taking a natural-scientific approach (Fuchs et al. 2007a) and refers to the physical susceptibility of elements at risk: Vulnerability means the degree of loss to a given element or set of elements at risk resulting from the impact of a natural hazard of a given frequency and magnitude, and is expressed on a scale from 0 (no damage) to 1 (total loss, Varnes 1984).

Recent empirical studies on vulnerability to torrent processes suggested a strong dependency of the degree of loss on the hazard impact (Fuchs et al. 2007a; Totschnig et al. 2011). Data from well-documented torrent events in the Austrian Alps were used to derive a quantitative vulnerability function applicable to buildings located on torrent fans. The method applied followed a geographical approach and was based on deposition heights as a proxy for process intensities, the spatial characteristics of elements at risk, average reconstruction values on a local scale, and loss data for each individual building affected. The results suggested different vulnerability functions for individual torrent processes. However, until now, no information is available on spatial characteristics of vulnerability within the concept of risk, apart from the overall (and empirically based) conclusion that low process intensities result in low damage ratio and therefore low vulnerability, and high process intensities in high damage ratio and consequently high vulnerability (e.g. Fuchs et al. 2007a). Since in particular medium process intensities between 1.00 and 2.00 m resulted in a considerable range in the associated damage ratio (Totschnig et al. 2011), there may be a dependency other than between process intensity and the damage ratio of the buildings exposed. Within this paper, we will therefore focus on the spatial dimension of vulnerability by searching for spatial clusters in the damage ratio of elements at risk exposed to torrent processes. As a hypothesis, we assume that the damage ratio of buildings is not randomly distributed over the torrent fan, instead, a spatial pattern will be traceable that is associated with but not entirely explainable through the occurring process intensity.

2 Study sites

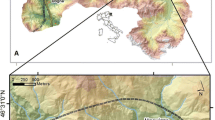
Data of four Austrian torrent catchments were included in this study (Fig. 1). These catchments were chosen because of (1) well-documented hazardous events causing (2) damage to buildings located on the respective torrent fans, which was (3) quantitatively collected in terms of monetary loss. The selected catchments are situated in the Western and Southern parts of the Republic of Austria in the Eastern European Alps.

Fig. 1
figure 1

Location of the study sites in the Austrian Alps, indicated by red dots. Layers comprising administrative bodies and shaded relief were provided by Environmental Systems Research Institute, Inc. (ESRI)

Full size image

The Vorderbergerbach torrent is located in southern Austria in the Federal State of Carinthia close to the city of Hermagor. The basin is part of the northern Carnic Alps, which represent the border to the Republic of Italy. The catchment area covers 25 km2 between 588 and 2,052 m a.s.l. Lithologically, the basin comprises mainly limestone of local type (Eder chalk) and Ordovician shale. The upper parts of the catchment are covered by glacial deposits from the Wurmian glaciation whereas the lower parts are characterised by Quaternary deposition of unconsolidated sediment (Hübl et al. 2004). Fluvial sediment transport processes are predominant in this watershed. The torrent Vorderbergerbach discharges within the municipality of Sankt Stefan into the Gail river. Although a number of damaging torrent events are recorded in the event registry (Hübl et al. 2004), the event of 29 August 2003 was used for this study.

The Stubenbach torrent is situated in the western part of Austria in the Federal State of Tyrol close to the Swiss border. The Stubenbach is a left tributary to the Inn river with a catchment area of 30 km2 between 1,011 and 3,035 m a.s.l. The catchment is part of the Samnaun mountain range, located within the so-called Engadin window, a Mesozoic ocean basin that was lifted and then over-thrusted by an older unit (Silvretta and Ötztal unit). The dominant lithology of the basin comprises several local types of shale with interbedded strata of quartzites (Bundesministerium für Land- und Forstwirtschaft 2006) and is covered by sediments of the Wurmian glaciation. The torrent Stubenbach is characterised by fluvial sediment transport processes and debris floods. The fan is located in the municipality of Pfunds, where several damaging torrent events are recorded in the event registry since 1831. The well-documented event of 22 August 2005 was used for this analysis.

The catchment of the Wartschenbach torrent is situated in the eastern Alps in the community of Nußdorf-Debant in the Drau valley, next to the city of Lienz, Federal State of Tyrol, Austria. The catchment covers an area of 2.3 km2 between 678 and 2,217 m a.s.l. The geology is dominated by para-gneiss and mica schist, and covered by glacial deposits (Gottschling 2003). Due to the considerable amount of unconsolidated material and to the steep gradient of 30–40%, the catchment is susceptible to erosion processes, in particular debris flows. Several damaging torrent events are recorded in the event registry. Apart from minor events, considerable losses in the Wartschensiedlung village located on the fan occurred during periods of high precipitation in 1972, 1981, 1995, 1997 (2x), 1998, 1999, and 2000. For this study, the events of 06 August 1995 and 16 August 1997 were used for the analysis since these events caused the severest damage and were therefore well documented.

The test site of Fimbabach/Trisanna is situated in the western part of Austria in the Federal State of Tyrol. The Fimbabach torrent catchment covers an area of 66 km2 between 1,349 and 3,399 m a.s.l., one-third of which is located on Swiss territory and partially glaciated. The basin is part of the Silvretta mountain range, and consequently, the geology is dominated by several local types of shale with interbedded strata of quartzites (Bundesministerium für Land- und Forstwirtschaft 2006) and covered by sediments of the Wurmian glaciation. The torrent Fimbabach is characterised by fluvial sediment transport processes. The fan is located in the municipality of Ischgl, where several damaging torrent events are recorded since 1833 (Hübl et al. 2006). The well-documented event of 22 August 2005 was used for this analysis. The majority of the affected buildings during this event are located in the area of confluence between Fimbabach and Trisanna river and hence are partly affected by flooding from both rivers.

A summary on the individual torrent events used in this study is provided in Table 1.

Table 1 Summary of damaging events that have been studied for the presented application of spatial scan statistics
Full size table

3 Methods

The assessment of vulnerability requires the evaluation of different parameters and factors such as type of element at risk, resistance, and implemented protective measures (i.e. local structural protection). With respect to the hazardous processes, empirical parameters such as magnitude and frequency have to be evaluated based on probability theory. Thereby the magnitude–frequency concept plays a key role: when the activity of different hazard processes is compared on a given timescale, some processes appear to operate continuously while others operate only when specific conditions occur. Torrent processes in European mountain regions are usually assessed by using a defined design event (Republik Österreich 1975; Schweizerische Eidgenossenschaft 1991; Repubblica Italiana 1998), which in case of Austria is the 1 in 150 year event (Republik Österreich 1976). Taking the perspective of natural sciences and neglecting any social implications arising from mountain hazards, vulnerability was considered as a functional relationship between the process magnitude or intensity, the resulting impact on structural elements at risk, and exposed values (Fuchs et al. 2007a; Totschnig et al. 2011). With respect to the built environment, vulnerability is related to the susceptibility of physical structures and is defined as the expected degree of loss resulting from the impact of a certain (design) event on the elements at risk (Fuchs 2009).

3.1 Damage ratio

Information on vulnerability can be assessed by analysing the damage ratio of well-documented hazard events. The damage ratio is defined as quotient between the loss that incurred during a specific event and the reinstatement value of an individual building.

The reinstatement value for the considered buildings in the study sites was assessed in a spatially explicit way by using GIS following suggestions outlined in Kranewitter (2002) as well as Keiler et al. (2006a, b).The sets of calculation were based on the building size, and an average value applied by Austrian building insurers of €1,670 per square metre was used as a basis for calculation of residential buildings (Totschnig et al. 2011). Commercial accommodation buildings were calculated on a slightly higher basis in a range between €1,837 and 2,506 per square metre depending on the facilities. The building size was derived from digital cadastral maps (scale 1:1,000) that were provided by the respective local community administration. As the spatial quality and temporal actuality of the cadastral maps were found to be variable, particularly with respect to the number of storeys, the building height, and the use of individual storeys as well as their state of repair, these data were updated by the interpretation of multi-temporal aerial photographs as well as field studies. The prices finally obtained represent reinstatement values of the individual buildings.

Loss data were collected using information derived from the respective administrative bodies of the individual Federal States of Austria. Professional damage appraisers of these administrative bodies estimated the loss of every individual element at risk in monetary terms on an object level in order to get information necessary for loss compensation.Footnote 2

As a result, the damage ratio for every building affected by the torrent events described in Sect. 2 was obtained.

3.2 Spatial scan statistics

Spatial scan statistics are widely used for detecting spatial clusters in data with geographical reference (Kulldorff 1997, 2010). Scan statistics are employed in order to test whether points are randomly distributed or clustered in space. In this study, the application was on point data that represent the damage ratio of every building affected by torrent hazards. We used the software SaTScan version 9.1 (Kulldorff 2010) to detect spatial distribution patterns of loss ratios on four torrent fans in Austria (Fig. 1) for five individual hazard events. Since the analysed data were related to individual buildings located on the torrent fans, we used the discrete scan statistics provided by SaTScan. This was done by gradually moving a window across space, calculating the number of observed and expected observations inside and outside the window for each location (irrespective of the underlying topography) for an ordinal data model. For a normal data model, the mean values of the studied phenomena inside and outside the scanning window were used instead.

The spatial extent of this window, and therefore the maximum spatial cluster size (MSCS), is variable. In SaTScan the MSCS can be chosen arbitrarily up to 50% of all cases by the analyst. However, O’Sullivan and Unwin (2003) pointed out that an analysis with varying scanning windows is subject to the modifiable area unit problem (MAUP), which is a general issue in spatial data analysis: the MAUP becomes relevant as soon as the shape or the size of an area examined can be modified since the aggregation of data changes when the size of the scanning window is modified, and therefore differences in the results may occur. This challenge was approached by scanning for several different MSCSs (20, 30, 40, and 50%) for each test site (Table 2). The results suggest that a variation in MSCS does not have any noteworthy influence on the number of cases, number of clusters, and significance levels of the p-values in each individual study site tested. The data were therefore considered as being stable, and the MAUP due to the variation of the window size is negligible. Consequently, we analysed our data with a MSCS of 50% according to a suggestion of Kulldorff (2010).

Table 2 Variations in the maximum spatial cluster size (MSCS) for each study site
Full size table

The output tables of the SaTScan software were further processed within a GIS environment for visualisation purpose.

3.2.1 Ordinal data model

In a first set of calculations, we applied an ordinal model for the analysis (Jung et al. 2007). With the ordinal model each observation is defined as a case, and each case belongs to one of three ordinal categories (high [3], medium [2], and low [1] damage ratio). These categories were tested individually against each other, or a combination of two categories was tested against the remaining one. We scanned over the study area in order to obtain clusters of high or low values. The applied method is based on a likelihood ratio test, and the most likely cluster is the area associated with the maximum value of the likelihood ratio test statistic. To find such a cluster, the scanning window was gradually moved across the data and the value of the likelihood was computed for every step. The collection of steps was interpreted as a parameter space for the cluster, over which the likelihood ratio is maximised (Jung et al. 2007). The size of the circular-shaped scanning window was variable up to a maximum of 50% of all cases observed on each individual torrent fan. The size of the ordinal categories was chosen by applying natural breaks to the loss data from each individual test site in order to mirror the site- and process-specific characteristics accordingly and to adjust for the unevenly distributed data with partially large jumps in values (Eck et al. 2005). The spatial distribution of loss categories was tested against each other, the likelihood functions were maximised over all scanning window locations, and the one with the maximum likelihood constituted the most likely cluster. In other words, this cluster was least likely to have occurred by chance, which in turn means that this cluster differs the most from the null-hypothesis, which was assumed to be a random distribution of the three categories of damage ratio over the torrent fans.

Formally, it was assumed that we have a study area composed of I sub-regions (buildings) and an outcome variable of interest (damage ratio) recorded in K categories. Following Jung et al. (2007), c ik is the number of observations in location i and category k, where i = 1,…,I and k = 1,…,K (in our study, k = 1,2,3). Since the categories are ordinal in nature, a larger k reflects a higher degree of loss. Furthermore, C i (\( = \sum\nolimits_{k} {c_{ik} } \)) is the total number of observations in location i (in our study: C i  = 1), C k (\( = \sum\nolimits_{i} {c_{ik} } \)) is the total number of observations in category k, and C (\( = \sum\nolimits_{k} {\sum\nolimits_{i} {c_{ik} } } \)) is the total number of observations on each individual torrent fan. The likelihood function for the ordinal model can be expressed as

$$ L(z,p_{1} , \ldots ,p_{K} ,q_{1} , \ldots ,q_{K} ) \propto \prod\limits_{k} {\left( {\prod\limits_{i \in z} {p_{k}^{{c_{ik} }} } \prod\limits_{i \notin z} {q_{k}^{{c_{ik} }} } } \right)} $$
(1)

where p k is the unknown probability that an observation within the scanning window z belongs to the category k, and q k is the unknown probability that an observation outside the scanning window z belongs to category k. Note that \( \sum\nolimits_{k} {p_{k} } = 1 \) and \( \sum\nolimits_{k} {q_{k} } = 1. \) The null-hypothesis is that the probability of being in category k within the scanning window is the same as outside the scanning window (H 0 : p 1  = q 1 ,…,p K  = q K ). The alternative hypothesis was considered as

$$ H_{a} :\frac{{p_{1} }}{{q_{1} }} \le \frac{{p_{2} }}{{q_{2} }} \le \cdots \le \frac{{p_{K} }}{{q_{K} }} $$
(2a)

or

$$ H_{a} :\frac{{p_{1} }}{{q_{1} }} \ge \frac{{p_{2} }}{{q_{2} }} \ge \cdots \ge \frac{{p_{K} }}{{q_{K} }} $$
(2b)

with at least one inequality being strict (Jung et al. 2007). This ensures that detected clusters represent an area with higher rates of high (Eq. 2a) or low (Eq. 2b) values of loss ratio than the surrounding area. The maximum likelihood ratio is expressed as

$$ \lambda = \frac{{\max_{{z,H_{a} }} L(z,p_{1} , \ldots ,p_{K} ,q_{1} , \ldots ,q_{K} )}}{{\max_{{z,H_{0} }} L(z,p_{1} , \ldots ,p_{K} ,q_{1} , \ldots ,q_{K} )}} = \max_{z} \frac{{L_{z} }}{{L_{0} }} $$
(3)

with

$$L_{0} = \prod\limits_{k} {\prod\limits_{i} {\hat{p}^{{c_{ik}}}_{o_{k}} } } = {\prod\limits_{k} {\left( {\frac{{C_{k} }}{C}}\right)} }^{{\sum_{i} c_{ik} }} = {\prod\limits_{k} {\left( {\frac{{C_{k} }}{C}} \right)}}^{{C_{k} }}$$
(4)

where \( \hat{p}_{o_{k}} = {{C_{k} } \mathord{\left/ {\vphantom {{C_{k} } C}} \right. \kern-\nulldelimiterspace} C}\left( { = \hat{q}_{o_{k}} } \right) \) is the maximum likelihood estimator of p k (=q k ) under the null-hypothesis, and with

$$ L_{z} = \prod\limits_{k} {\left( {\prod\limits_{i \in z} {\hat{p}_{k}^{{c_{ik} }} } \prod\limits_{i \notin z} {\hat{q}_{k}^{{c_{ik} }} } } \right)} $$
(5)

where \( \hat{p}_{k} \) and \( \hat{q}_{k} \) are the maximum likelihood estimators under the alternative hypothesis (Jung et al. 2007). The larger the λ, the higher the probability of the alternative hypothesis to be true for the most likely cluster in a certain area and for a certain category or combination of categories.

The p value indicating the statistical significance of a cluster was obtained through Monte Carlo hypothesis testing by computing the maximum likelihoods of a large number of random replications of the data set under the null-hypothesis for comparison with the rank of the maximum likelihood from the real data set (Kulldorff 2010). As a result, primary and secondary clusters for the spatial distribution of damage ratios were obtained for each individual torrent fan, the primary cluster being the most likely cluster and the secondary ones being all other clusters sorted in a decreasing order by their p value.

3.2.2 Normal data model

In a second set of calculations, we applied a normal model for the analysis of continuous data (Kulldorff et al. 2009). With the normal model, each observation is defined as a case, and for all cases an attribute (the damage ratio) was tested. Under the null-hypothesis, all attributes are distributed within the studied area following a normal distribution. Under the alternative hypothesis, there are cluster areas where the individual damage ratios have either a larger or smaller mean than outside the cluster. We scanned for areas of such larger or smaller means of the damage ratio with the size of the circular-shaped scanning window being variable up to a maximum of 50% of all cases observed on each individual torrent fan. The applied method is based on a log likelihood ratio test, whereas the most likely cluster is the area associated with the maximum value of the log likelihood ratio test statistic. At first, the maximum (log) likelihood estimates of the mean inside and outside the circle and the variance were calculated under the null-hypothesis for the entire data set and under the alternative hypothesis for each specific cluster circle. Subsequently, the circular scanning window was gradually moved across the data using the maximum log likelihood ratio for each circle as a test statistic. The resulting values were then compared to the maximum likelihood estimates of the mean and variance under the previously obtained values under the null-hypothesis and the alternative hypothesis, respectively.

Formally, it was assumed that we have a study area composed of I locations (buildings) with data having continuous observations (damage ratio) with values x d , where d = 1,…, N. For each location i, the sum of the observed values is defined as \( x_{i} = \sum\nolimits_{d \in i} {x_{d} } \), and the number of observations in the location i as n i (in our study, n i  = 1 since every building was characterised by one damage ratio). The sum of all observed values is \( X = \sum\nolimits_{d} {x_{d} } \). Let \( n_{z} = \sum\nolimits_{i \in z} {n_{i} } \) be the number of observations in each scanning window z, and let \( x_{z} = \sum\nolimits_{i \in z} {x_{i} } \) be the sum of the observed values in each scanning window z.

Under the null-hypothesis, the maximum likelihood estimates of the mean and the variance are μ = X/N and \( \sigma^{2} = \frac{{\sum\nolimits_{d} {\left( {\mu - x_{d} } \right)} }}{N}^{2} \), respectively (Kulldorff et al. 2009). The likelihood under the null-hypothesis is then

$$ L_{0} = \prod\limits_{d} {\frac{1}{{\sigma \sqrt {2\pi } }}{\text{e}}}^{{ - \frac{{\mathop {(x_{d} - \mu )}\nolimits^{2} }}{{\mathop {2\sigma }\nolimits^{2} }}}} $$
(6)

and the log likelihood is

$$ \ln L_{0} = - N\ln \left( {\sqrt {2\pi } } \right) - N\ln \left( \sigma \right) - \sum\limits_{d} {\frac{{\left( {x_{d} - \mu } \right)^{2} }}{{2\sigma^{2} }}} $$
(7)

Under the alternative hypothesis, we first calculate the maximum likelihood estimators that are specific to each scanning window circle z, which is μ z  = x z /n z for the mean inside the circle and λ z  = (X − x z )/(N − n z ) for the mean outside the circle. The maximum likelihood estimate for the common variance is

$$ \sigma_{z}^{2} = \frac{1}{N}\left( {\sum\limits_{d \in z} {x_{d}^{2} - 2x_{z} \mu_{z} } + n_{z} \mu_{z}^{2} + \sum\limits_{d \notin z} {x_{d}^{2} - 2\left( {X - x_{z} } \right)} \lambda_{z} + \left( {N - n_{z} } \right)\lambda_{z}^{2} } \right) $$
(8)

The log likelihood for the scanning window circle z in a simplified form is

$$ \ln L_{z} = - N\ln \left(\sqrt {2\pi }\right) - N\ln\left(\sqrt{\sigma_{z}^{2} }\right) - N/2 $$
(9)

As the test statistic, we use the maximum likelihood ratio \( \max_{z} \left( {L_{z} /L_{0} } \right) \) or, as suggested by Kulldorff et al. (2009), more conveniently but equivalently, the maximum log likelihood ratio

$$ \max_{z} \frac{{\ln L_{z} }}{{\ln L_{0} }} $$
(10)

The inference of the maximum log likelihood ratio is then calculated through a permutation-based Monte Carlo hypothesis testing. This is a key feature of the method assuring that although the true distribution of the data is not normal (such as in our study), the correct α level is maintained. This is due to the simulation procedure, where a large set of random data sets is created by randomly permuting the observed values x d and their corresponding locations i, rather than generating random data from the normal distribution (Kulldorff et al. 2009).

4 Results

The analysis of four study sites and five torrent events resulted in an overall amount of 178 damaged buildings, 135 of which were included in the sets of calculation. The overall analysis of the damages within the study sites had shown that two-third of all losses incurred due to an intrusion of material into the building (Fig. 2). Even if obvious, this fact has only been qualitatively described so far (Holub and Fuchs 2009), and it clearly shows the potential for local structural protection to prevent major losses (Holub and Fuchs 2008; Fuchs 2009). If during an event material entered through building openings, the overall range of the damage ratio is remarkably high compared with buildings where such an intrusion could not be proven (Fig. 2, Fuchs et al. 2007a). Furthermore, the damage patterns and as a consequence the damage ratio were dependent on the process characteristics observed: While the Vorderbergerbach event only exhibited a minor range of process intensities, resulting in minor damage ratios, other events were characterised by higher ranges in process intensities and therefore showed higher damage ratios (see Tables 3 and 4).

Fig. 2
figure 2

Boxplots of the damage ratio for the entire data set (all torrent events), differentiating between cases with and without intrusion of material into the building

Full size image
Table 3 Summary of the results from the application of the ordinal data model
Full size table
Table 4 Summary of the results from the application of the normal probability model
Full size table

4.1 Ordinal data model

This distinction between the study sites had also been mirrored by the threshold values for the damage ratio applied during the ordinal data model by using natural breaks for the individual torrent events (Table 3). While for the Vorderbergerbach catchment, the class of high damage ratio spanned between 0.028 and 0.050, for the other catchments this class was >0.216 (Stubenbach, 0.475–1.000; Wartschenbach ‘95, 0.216–0.344; Wartschenbach ‘97, 0.340–0.570; Fimbabach/Trisanna, 0.242–0.656). Again, this is in part a result of the process characteristics in the different sites included in this study.

By using a 50% scanning window, which included a maximum spatial cluster size of 50% of all cases, only in two catchments (Stubenbach and Fimbabach/Trisanna) a significant most likely cluster was detected. Significance was defined by a level of α < 0.05 (significant) and <0.01 (highly significant). For all catchments and events, clusters of high values of damage ratios (Vorderbergerbach, 2; Stubenbach, 3; Wartschenbach ‘95, 1; Wartschenbach ‘97, 1; Fimbabach/Trisanna, 1) were detected, while clusters of low values of damage ratios were only identified for four events (Vorderbergerbach, 1; Stubenbach, 1; Wartschenbach ‘97, 1; Fimbabach/Trisanna, 2). Since this study was performed on a local scale, the cluster radius is relatively small (21–110 m with the exception of Fimbabach/Trisanna were the losses occurred over a larger area, and therefore one cluster radius was 1,200 m). The size of the cluster radii was also a result of both the presumption that no geographical overlap between clusters is allowed and the settlement structure in the study areas.

The detection of significant clusters implies that the null-hypothesis of random distribution of damage ratios over corresponding individual torrent fans has to be rejected. This suggests that the damage ratio is a result of specific process magnitudes in combination with specific characteristics of the damaged element at risk, both of which leading to a spatial concentration of high or low values of damage ratios for an individual torrent event. In Fig. 3, an overview of the individual results is provided. The inference was performed by applying a Monte Carlo simulation with 999 replications.

Fig. 3
figure 3

Results from the application of the ordinal data model. In squared brackets the categories of damage ratio are provided for each individual test site. Clusters that were detected are indicated with respect to these categories, for example, [1, 2], [3] means that a cluster is detected if the damage categories [1] and [2] are jointly tested against category [3]. For each cluster, the p value indicating the level of significance is given

Full size image
  1. (a)

    In the Vorderbergerbach study area, clusters with high or low values were detected, and the classes of damage ratio included 17, 7, and 6 buildings (low [1], medium [2], and high [3]). The two clusters of high values included 5 (p value 0.264, most likely cluster) and 4 (p value 0.701, secondary cluster) buildings, and the cluster of low values included 5 buildings (p value 0.895, secondary cluster).

  2. (b)

    In the Stubenbach study area, clusters with high or low values were detected, and the classes of damage ratio included 20, 8, and 11 buildings (low, medium, and high). The three clusters of high values included 10 (p value 0.022, most likely and significant cluster), 2 (p value 0.992, secondary cluster), and 3 (p value 0.999, secondary cluster) buildings, and the cluster of low values included 6 buildings (p value 0.539, secondary cluster).

  3. (c)

    In the Wartschenbach catchment, two torrent events were analysed. For the event of 1995, the classes of damage ratio included 5, 3, and 2 buildings (low, medium, and high) and one cluster of high values was detected. This cluster included 3 buildings (p value 0.728).

  4. (d)

    For the event of 1997, the classes of damage ratio included 7, 5, and 4 buildings (low, medium, and high) and one cluster of high values was detected. This cluster included 7 buildings (p value 0.072, most likely cluster). One secondary cluster of low values was detected, which included 2 buildings (p value 0.999).

  5. (e)

    In the Fimbabach/Trisanna study area, clusters with high or low values were detected and the classes of damage ratio included 17, 15, and 8 buildings (low, medium, and high). One highly significant cluster of high values (9 buildings, p value 0.001) and two secondary clusters were detected. These secondary clusters included 20 (p value 0.115) and 5 (p value 0.422) buildings.

4.2 Normal data model

The application of the normal data model resulted in distinct differences between the torrent events studied (Table 4). By using a 50% scanning window, which included a maximum spatial cluster size of 50% of all cases, in two catchments (Stubenbach and Wartschenbach ‘97), a significant most likely cluster was detected. For the catchment of Fimbabach/Trisanna, a highly significant most likely cluster was identified. The significance level was defined as α < 0.05 (significant) and <0.01 (highly significant). For all catchments and events, clusters of high values of damage ratios (Vorderbergerbach, 1; Stubenbach, 2; Wartschenbach ‘95, 1; Wartschenbach ‘97, 1; Fimbabach/Trisanna, 1) were detected. One cluster of low values of damage ratios was identified in each test site. Since this study was performed on a local scale, the cluster radius is relatively small (24–200 m with the exception of Fimbabach/Trisanna where the losses occurred over a larger area, and therefore one cluster radius was 730 m, and Vorderbergerbach where one cluster radius equalled 370 m). The size of the cluster radii was also a result of both the presumption that no geographical overlap between clusters is allowed and the settlement structure in the study areas.

The detection of significant clusters implies that the null-hypothesis of random distribution of damage ratios over corresponding individual torrent fans has to be rejected. This suggests that the damage ratio is a result of specific process magnitudes in combination with specific characteristics of the damaged element at risk, both of which leading to a spatial concentration of high or low values of damage ratios for an individual torrent event. In Fig. 4, an overview of the individual results is provided. The inference was again performed by applying a Monte Carlo simulation with 999 replications in order to allow for comparisons between the ordinal and normal models.

Fig. 4
figure 4

Results from the application of the normal data model. The level of significance is provided for each detected cluster by the p value. Note: damage categories are only provided for visual purpose, the calculation was based on the mean value of the entire dataset versus the mean value inside the gradually moved scanning window

Full size image
  1. (a)

    In the Vorderbergerbach study area, clusters with high or low values were detected. The cluster of high values included 11 buildings (p value 0.135, most likely cluster), and the cluster of low values included 14 buildings (p value 0.807, secondary cluster).

  2. (b)

    In the Stubenbach study area, clusters with high or low values were detected. The cluster of high values included 7 (p value 0.041, most likely and significant cluster) buildings. Two secondary clusters resulted, one of high values including 3 buildings (p value 0.993, secondary cluster), and one of low values including 10 buildings (p value 0.291, secondary cluster).

  3. (c)

    In the Wartschenbach catchment, two torrent events were analysed, both of which resulted in one cluster of high values and one cluster of low values. For the event of 1995, the cluster of high values included 5 buildings (p value 0.740, most likely cluster) and the cluster of low values included 2 buildings (p value 0.941, secondary cluster).

  4. (d)

    For the event of 1997, a cluster of high values with 7 buildings (p value 0.039, most likely and significant cluster) and a cluster of low values with 2 buildings (p value 0.995, secondary cluster) were found.

  5. (e)

    In the Fimbabach/Trisanna study area, clusters with high or low values were detected. The cluster of high values included 9 buildings (p value 0.001, most likely and highly significant cluster), and the cluster of low values included 19 buildings (p value 0.589, secondary cluster).

5 Discussion and conclusion

Within this paper, spatial patterns of damage to buildings located in settlements that were suffering from torrential hazards were analysed. An ex post spatial scan statistics was performed for five well-documented events that recently occurred in the Austrian Alps. Therefore, geographical data on individual elements at risk located on torrent fans, the respective reconstruction value, the loss height, and event characteristics such as the process magnitude were analysed. By applying an ordinal and a normal probability model, clusters of high and low damage ratios resulted in all study sites, and it was demonstrated that the null-hypothesis of random spatial distribution had to be rejected for two catchments while for the other events, only clusters beyond the level of significance were proven. Similarly, the normal data model resulted in two significant clusters and one highly significant cluster of high values. Nevertheless, the results are in accordance with earlier studies on vulnerability of buildings exposed to torrent events in the European Alps (e.g. Fuchs 2008; Quan Luna et al. 2011; Totschnig et al. 2011) and beyond (Liu 2006; Chen et al. 2010). These studies were focusing on a dependency of the damage ratio on the process magnitude and were targeted at the deduction of a general functional relationship between these two parameters. Thus, they were aimed at a generalised vulnerability function for use in mountain hazard risk management. However, a considerable range occurred with respect to medium process intensities, and as such, our study was focusing on spatial differences that may be used to explain these high ranges at the local level of individual torrent fans.

Generally, we suggest the use of the normal data model if the underlying data on vulnerability are continuous, since the aggregation to categories (e.g. by natural breaks) leads to a loss in information. Only in such cases where this data already are categorised, the use of the ordinal data model is proposed (e.g. with respect to the Swiss guidelines for mountain hazard risk assessment, Bründl et al. 2009).

Both the ordinal and the normal probability models detected clusters at similar locations (Figs. 3, 4c, d, e). Even if some clusters were found for slightly different areas in the Vorderbergerbach and Stubenbach test site (Figs. 3, 4a, b), their most likely cluster locations mainly coincided. More precisely, differences in the results between the ordinal and the normal models only arose with respect to clusters with a high p value, for example Vorderbergerbach, cluster C (p = 0.895) versus cluster B (p = 0.807) and Stubenbach, cluster D (p = 0.999) versus cluster C (p = 0.993). As a consequence, the geographical location and size of the most likely clusters are more important with respect to the analysis of spatial patterns in vulnerability, irrespectively of being a cluster of high or low values.

If the clusters of the damage ratio are overlain with the process magnitude of the individual hazard event, a spatial consistency is proven (Fig. 5). As demonstrated for the example of Vorderbergerbach, higher damage ratios were identified in areas with a higher process magnitude and one most likely cluster of high values was detected. On the other hand, vulnerability is also dependent on the properties of the elements at risk affected; therefore, higher damage ratios also occurred in less torrent-prone locations, and locations with low process intensities were not necessarily detected by SaTScan as low-rate clusters. Hence, the overall assumption that low process intensities result in low damage ratios, and therefore in low vulnerability, and vice versa for high process intensities, has to be rejected. The spatial distribution of geographical locations with either high or low damage ratios is not only an effect of changing process intensities, but also an outcome of the general land use pattern on each individual torrent fan and the overall constructive characteristics of the elements at risk. As such, the study enhanced our understanding of vulnerability patterns on a local scale. Moreover, as further studies may include the overall settlement pattern in the sets of calculation, an in-depth understanding of vulnerability will be achieved.

Fig. 5
figure 5

Clusters detected by the normal data model in comparison with the event documentation (process magnitude) of 29 August 2003 in the Vorderbergerbach catchment. The blue arrow indicates the flow direction. Note: the considerable deposition height on the northern margin of the settlement was caused by ponding behind a levee originally implemented to protect the settlement against flooding from the Gail river (receiving stream of Vorderbergerbach)

Full size image

It had been demonstrated that the approach of spatial scan statistics is suitable even for a restricted amount of spatial data available on a local scale. Nevertheless, for the application of both data models, a sufficient amount of data is needed. In this study, we found a number of 30 cases to be a minimum for a reasonable use of the spatial scan statistic. As shown in Figs. 3 and 4, the clusters detected in the Wartschenbach test site (‘95 and ‘97) are not conclusive for a comprehensive analysis of spatial vulnerability patterns. Therefore, in order to avoid these constraints, more well-documented events have to be collected. Moreover, such restrictions may be a major concern with respect to scale since local assessments of natural hazard vulnerability are hardly comparable with studies undertaken on a regional scale (Cutter and Finch 2008; Stevenson et al. 2010). Additionally, a further analysis of data, such as according to the type and year of construction, would enrich our understanding beyond space; such information would be of particular interest with respect to the overall discussion on multi-temporal and spatial assessment of risk (Fuchs et al. 2005; Keiler et al. 2005, 2006a; Zischg et al. 2005a, b), and with respect to advances in multi-temporal vulnerability assessments (Fuchs et al. 2011; Papathoma-Köhle et al. 2011) and multi-hazard vulnerability studies (Kappes et al. 2011).