1 Introduction

During the last decades, an increase in land-use activity could be observed in European mountain regions. Taking the Republic of Austria as an example, settlements have been expanded, leading to extensive land consumption and associated population growth. Since the 1970s, the average useable living space increased from 22 m2 per person in 1972 to 38 m2 in 2001 (Statistik Austria 2004). As a major part of Austria is located in mountain areas above 1,000 m a.s.l. (this is approximately 36% of the territory, and approximately 19% of it is located above 1,500 m a.s.l.), areas appropriate for permanent settlement are limited (Holub and Fuchs 2009). In the entire country, 37.2% of the land area is suitable for permanent settlement and associated economic activities, while in some Federal States, the values remain noticeably below one-third of the area. Due to this scarcity, land-use activities have repeatedly been extended into areas, which are endangered by natural hazards such as mass movements, torrent processes, and avalanches. As a consequence, property values prone to these processes increased accordingly (Fuchs et al. 2005; Keiler et al. 2006a).

Until now, only few studies addressed the development of natural hazard events and associated losses in alpine countries. These studies were mostly focused on distinct events or reference periods, not on assessing the topic from a broader point of view by compiling a comprehensive database, e.g., SLF (2000), Nöthiger et al. (2002), Fuchs and Bründl (2005), and Hilker et al. (2009) for Switzerland, as well as Embleton-Hamann (1997), Fliri (1998), Luzian (2002), and Oberndorfer et al. (2007) for Austria. Though, with respect to the concept of integral risk management, such information is required in order to be able to plan and implement sustainable mitigation strategies. Sustainable mitigation strategies, as outlined by Holub and Fuchs (2009) in more detail, have to be pillared on a complementary multiplicity of risk treatment options acting upon the maxim of cost efficiency in relation to the targeted expenditures and the aspired decrease in risk. Given the significance of these expenditures, risk-based appraisal of the costs and benefits (in terms of risk reduction) of major capital works is now customary in many alpine countries (e.g., Haering et al. 2002; BMLFUW 2005), although vulnerability assessment and partly hazard analysis is still in need of improvement.

In Austria, two comprehensive databases on torrent events exist. A database of destructive torrent events was established on the basis of information from the Austrian Torrent and Avalanche Control ServiceFootnote 1 and analysed concerning monetary losses by Oberndorfer et al. (2007). A total number of 4,894 damaging torrent events were reported between 1972 and 2004. For almost 4,300 events, the process type could be determined ex-post due to the event documentation carried out by the Austrian Torrent and Avalanche Control Service. This resulted in a classification between floods (0.3%), flooding with bedload transport (21.8%), hyperconcentrated flows (49.2%), and debris flows (28.7%). The average direct loss per event due to these 4,300 records amounted to approximately € 170,000 (in 2009 values), and annual losses due to torrent events amounted to around € 25 million. Approximately two-thirds of the losses could be ascribed to buildings and one-third to infrastructure facilities (Fuchs 2009). Within the period under investigation, 21 people were physically harmed and 49 people died. The annual distribution of the losses showed that considerable cumulative damage exceeding € 1 million per event occurred in 1975, 1978 and 1991. In contrast, in 1976 and 1984, the average damage per event summed up to € 11,000 and € 16,000, respectively. A considerable number of events were reported from 1974, 1990 and 2002, leading to the conclusion that a high number of events do not necessarily result in high losses, and vice versa.

A second database was derived from a reanalysis of written reports, which were compiled during the implementation of hazard maps by the Austrian Torrent and Avalanche Control Service and completed by the integration of additional historical sources (Hübl et al. 2010). The analysis of these data had shown a decreasing trend related to the overall number, which was exceeding twice the number of the database analysed by Oberndorfer et al. (2007) [N = 11,185; annual mean = 186]. However, considerable events were observed in individual years, in particular, in the western part of Austria (see Fig. 1). An above-average number of events were reported from 1959, 1965, 1966, 1975, 1991, 2002 and 2005.

Fig. 1
figure 1

Data related to torrent events collected from the reports which were compiled during the implementation of hazard maps by the Austrian Torrent and Avalanche Control Service for the period 1950–2009 (illustrated on a district level). Even if a spatial concentration of events can be proven for the western part of Austria, the overall trend is decreasing, which is in line with studies by Oberndorfer et al. (2007) although their studies were based on another universal set of data. With respect to avalanches, an equivalent decrease was reported by Fuchs and Bründl (2005) for the western part of Switzerland (Data source: Institute of Mountain Risk Engineering, University of Natural Resources and Life Sciences, Vienna)

Full size image

Obviously, the two data sets show some similarities and some differences even if they theoretically root in the same set of data. Despite these databases, which are not consistent if compared to each other, and besides many national and European efforts to reduce natural hazard impact on society (Commission of the European Communities 2007), considerable damage has still occurred in recent years in European mountain regions. Particularly in the 1990s, substantial damage occurred all over the Alps due to avalanches (winter 1998/1999), torrent processes (1999, 2002, 2005) and inundation (2002, 2005, 2006), even though the overall amount of losses was moderate compared to previous decades. Consequently, greater availability of information of natural hazard occurrence on a scientific basis but also due to broader media coverage resulted in an increase in hazard awareness on a societal level, in particular due to a perceived increase in property damage and fatalities. As a result, the general public progressively more realised—also on the political level—that a complete protection against natural hazards is neither socially affordable nor economically justifiable (cf. Fuchs and McAlpin 2005). People and political decision-makers have become more and more aware of the impacts resulting from hazards and thus in some Alpine countries a paradigm shift from hazard reduction to a risk culture has been initiated (e.g., by political action, cf. PLANAT 2004 in response to Nationalrat 2000).

The shift from hazard to risk obviously requires a completely different approach with respect to necessary management issues. The concept of risk, defined as a function of hazard and consequences, seems to be a suitable and promising approach with respect to these needs. Despite the comprehensive experiences that have been made by applying the concept of risk to mountain hazard management, in particular in Switzerland (Kienholz 1994; Hollenstein 1995; Heinimann 1998), considerable questions with respect to the methods developed for an operational implementation of the risk concept still remain open.

The review of the concept of risk of alpine countries resulted in gaps concerning appropriate tools for the assessment of vulnerability of elements at risk and of communities exposed. To overcome these shortcomings, studies on vulnerability have been undertaken aiming at (1) the methodological development of loss functions with respect to buildings located in the run-out areas of torrent processes (Fuchs et al. 2007a); and (2) the conceptualisation of an overarching vulnerability model including structural, economic, social and institutional vulnerability (Fuchs 2009).

Focusing on the first, and expanding previous results published by Fuchs et al. (2007a), data related to losses originating from three torrents in Austria were analysed with respect to process intensities and the elements at risk exposed. The study followed a spatial approach and focused on the implementation of a vulnerability function in order to improve hazard and risk assessment for alpine torrents. A spatial approach is thereby understood as a spatially explicit determination of the involved variables using a GIS environment.

2 Methodology

Vulnerability functions are developed to link the susceptibility of elements at risk to the magnitude of the respective hazardous processes and are used within integral risk management to quantitatively assess individual and collective risk.

For torrent processes, mainly qualitative and semi-quantitative methods are available so far for the quantification of vulnerability towards debris flow processes, for an overview compare Fuchs et al. (2007a). Due to these shortcomings, Fuchs et al. (2007a) developed a quantitative vulnerability function for alpine debris flows in Austria, which was applied by Akbas et al. (2009) using data from the Italian Alps and by Tsao et al. (2010) using data from Taiwan. However, only little information is available until now with respect to other torrent processes, particularly fluvial sediment transport, even if considerable amounts of damage can be ascribed to this process type. Hence, the overall objective of this study was to provide such data in order to compile comprehensive information on physical vulnerability of elements at risk located on alpine torrent fans.

2.1 Fluvial sediment transport

In a European context, the term torrent refers to steep rivers within a mountainous environment. Torrents are defined as constantly or temporarily flowing watercourses with strongly changing perennial or intermittent discharge and flow conditions (Aulitzky 1980; ONR 2009), originating within small catchment areas (Slaymaker 1988). Catchment characteristics, such as watershed area and longitudinal slope, are alternatively used to define torrents, whereas the delimitation criteria are often not as clear. While some authors refer only to the area of the watershed for a delimitation of torrents from other types of linear watercourses, others additionally include information on the longitudinal slope (see Table 1).

Table 1 Definition of torrents based on implicit (♣) and explicit (♦) classification
Full size table

Torrent events include a process group, which shows a variety of different flow characteristics including discharge composed from pure water run-off, discharge with variable sediment concentration and debris flows (Costa 1984). Therefore, the major characteristics of the respective events in the different test sites have to be defined. The sediment concentration is employed in conventional engineering approaches to distinguish between different processes, although the use of one individual parameter as a decision rule is reported to be insufficient (Costa 1984). However, Hungr et al. (2001) recommend peak discharge as a reliable criterion to differentiate between different process types, i.e., debris flows and debris floods.

While debris floods are usually associated with considerable transport of coarse sediment, hyperconcentrated flows, partly used as a synonym for debris floods (Costa 1984, 1988), are characterised by larger amounts of fine sediment in suspension (Scheidl and Rickenmann 2010). A sediment concentration of 70% by weight (47% by volume) as a threshold between hyperconcentrated flows and debris flows is suggested (Costa 1988). In this study, the understanding of the terms debris flow and debris flood is based on the classification presented by Hungr et al. (2001): While debris floods typically produce relatively thin, wide sheets of material, debris flows produce thicker, more hummocky and lobate depositions.

Fluvial sediment transport, in contrast, also referred to as water floods (Costa 1988) or sediment-laden flow (Wan and Wang 1994), is characterised by a lower sediment concentration than debris floods (Scheidl and Rickenmann 2010). A sediment concentration of 40% by weight (20% by volume) as a threshold between fluvial sediment transport and hyperconcentrated flows is suggested (Costa 1988). Within fluvial sediment transport processes, sediment and water are moving with different velocities as two distinct and separate phases (Costa 1988). During one individual event, the respective processes in the torrent often change due to the temporal and spatial variability of sediment concentration. As a result, the dominant process in the central part of the deposition zone should be used to define the entire event characteristics (Hungr et al. 2001). However, sediment concentration (Costa 1984, 1988) and peak discharge (Hungr et al. 2001) cannot be determined for historical events, nor are such characteristics widely used in recent event documentations. Due to this lack of data, an alternative procedure to determine the general predisposition of a catchment to a certain torrent process was applied. This approach is based on a relation between the Melton number M E and the average fan slope S f (Bardou 2002), see Fig. 2. The Melton number M E resulted from a combination of maximum elevation difference in a catchment divided by the square root of the catchment area according to Melton’s ruggedness number (Melton 1965) and represents a relative and dimensionless parameter for the basin relief. Two threshold lines were proposed to distinguish between different torrent processes (Fig. 2). By threshold line A fluvial sediment transport processes are separated from mixed processes, and by threshold line B mixed processes are separated from debris flows (Bardou 2002; Scheidl and Rickenmann 2010).Footnote 2 A Melton number below 0.3 is typical for watersheds dominated by fluvial sediment transport (Wilford et al. 2004). It is shown in Fig. 2 that two test sites (Vorderbergerbach and Stubenbach, see Sect. 2.2) are situated within or close to the area of fluvial sediment transport processes. Simultaneously, the Melton number of these two test sites is below or close to 0.3, which is a further indication for a general predisposition of these catchments towards fluvial sediment transport processes. As indicated in Fig. 2, the Schnannerbach torrent is situated in the area of mixed transport processes.

Fig. 2
figure 2

Relation between average fan slope and Melton number of the three test sites in comparison with results from the literature indicated. Threshold line A separates fluvial sediment transport processes from mixed processes, and threshold line B separates mixed processes from debris flows. The following abbreviations were used: DF debris flow, DFL debris flood and FST fluvial sediment transport, M E Melton number, S f average fan slope (modified from Scheidl and Rickenmann 2010)

Full size image

2.2 Test sites

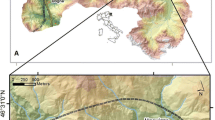
Event data of three Austrian torrent catchments were included in this study. To be applicable for this study, the test sites had to fulfil the following requirements: (1) well-documented events; (2) incurring damage on dwelling houses caused by fluvial sediment transport processes; and (3) damage quantitatively registered in terms of monetary loss. The selected catchments are situated in the western and southern parts of the Republic of Austria in the provinces of Tyrol and Carinthia (Fig. 3). The general morphometric parameters of the catchments are given in Table 2.

Fig. 3
figure 3

Location of the test sites in the Austrian Alps, indicated by red dots. Layers comprising administrative bodies and shaded relief provided by Environmental Systems Research Institute, Inc. (ESRI)

Full size image
Table 2 General morphometric parameters of the catchments including Melton number and average fan slope
Full size table

The Vorderbergerbach torrent is located in southern Austria in the province of Carinthia close to the city of Hermagor. The basin is part of the northern Carnic Alps, which represent the border to Italy. Lithologically, the basin comprises mainly limestone of local type (Eder chalk) and Ordovician shale. The upper parts of the catchment are covered by glacial deposits from the Wurmian glaciation, whereas the lower parts are characterised by Quaternary deposition of unconsolidated sediment (Hübl et al. 2004). Fluvial sediment transport processes are predominant in this watershed. The torrent Vorderbergerbach discharges within the municipality of Sankt Stefan into the Gail river. Although a number of damaging torrent events are recorded in the event registry (Hübl et al. 2004), the event of 29 August 2003 was used for this study due to the availability of respective data.

The Stubenbach torrent is situated in the western part of Austria in the province of Tyrol close to the Swiss border. The basin is part of the Samnaun mountain range. Geologically, the basin is located within the Engadin window, a Mesozoic ocean basin, which was lifted and then over-thrusted by older layers (Silvretta and Ötztal layer). The dominant lithology of the basin comprises several local types of shale with interbedded strata of quartzites (BMLFUW 2006). The torrent Stubenbach, characterised by fluvial sediment transport processes and debris floods, is a tributary of the Inn river. The fan is located in the municipality of Pfunds, where several damaging torrent events are recorded in the event registry since 1831. The well-documented event of 22 August 2005 was used for this analysis (Fig. 4).

Fig. 4
figure 4

The event of 22 August 2005 at the Stubenbach torrent in the municipality of Pfunds (courtesy of ASI Tirol)

Full size image

The Schnannerbach torrent is located in the western part of Austria in the province of Tyrol close to the city of Landeck. The basin is part of the Lechtaler Alps. The lithology of the Lechtaler Alps comprises mainly limestone, dolomite, marl, shale and sandstone. The headwater of the torrent consists of several small creeks, and the sediment transported downstream originates from large talus cones in the upper part of the catchment. The middle reaches of the Schnannerbach torrent are characterised by a gorge cut into bedrock, and the torrent discharges via its own fan into the Rosanna river (BMLFUW 2006; Hübl et al. 2006). The fan is located in the municipality of Pettneu am Arlberg, where several damaging torrent events are recorded since 1852. For this study, the event of 22 August 2005 was chosen.

Fluvial sediment transport was found to be the dominant process in the accumulation area of the considered events. The low sediment concentration and the typical two-phase regime observed proved this process classification. Using the Melton number and a relation between Melton number and the average fan slope, a general predisposition of the Vorderbergerbach torrent and the Stubenbach torrent towards fluvial sediment transport processes is evident (Fig. 2). Although the Schnannerbach torrent generally tends to debris floods (Fig. 2), the low sediment availability of the considered event resulted in a fluvial sediment transport process (Hübl et al. 2006). The back-calculated sediment concentration based on water and sediment volume of this event is equal to approximately 2% (Chiari and Rickenmann 2007).

2.3 Quantification of vulnerability

Following the axiom that natural hazard risk is a function of hazard and consequences, the ability to determine vulnerability either quantitatively or qualitatively is an essential prerequisite for reducing these consequences and therefore natural hazard risk. The assessment of vulnerability requires an ability to both identify and understand the susceptibility of elements at risk and—in a broader sense—of the society to these hazards (Birkmann 2006). Studies related to vulnerability of human and natural systems to mountain hazards, and of the ability of these systems to adapt to changes in the functional chain of hazards, are a relatively recent field of research that brings together experts from a wide range of disciplines, including natural science, social science, disaster management, policy development and economics, to name only a few. Researchers from these fields bring their own conceptual models to study vulnerability and adaptation, models which often address similar problems and processes using different languages (Brooks 2003). However, apart from the overall discussion on linguistic placements and semantic dimensions of the term (Cutter 1996, 2003; Alexander 2005), vulnerability in the context of mountain natural hazards in Europe is, from a practitioner’s side such as the Austrian Torrent and Avalanche Control Service, usually defined as the physical impact of hazardous events on elements at risk. Accordingly, if quantitatively assessed, vulnerability is defined as the expected degree of loss for an element at risk due to the impact of a defined hazardous event within a defined period of time and a defined location. These events are themselves conditioned by a certain intensity, frequency and duration, all of which affect vulnerability. From this technical point of view, as a general rule, vulnerability assessment is based on the evaluation of parameters and factors such as building categories or types, construction materials and techniques, state of maintenance, presence of protection structures and presence of warning systems (Fell et al. 2008). For this reason, vulnerability values describe the susceptibility of elements at risk to damage, which is conceptualised by a damage ratio between loss and the value of affected elements at risk, facing different process types with different spatial and temporal distributions of process intensities (e.g., flow depths, accumulation heights, flow velocities and pressures).

The damage ratio was quantified using an economic approach by establishing a ratio between the loss and the reconstruction value of every individual element at risk exposed. In a second set of calculations, this ratio obtained for every individual element at risk was attributed to the respective process intensities. The relation between damage ratio and process intensity was defined as vulnerability. Therefore, information on the elements at risk exposed on the individual torrent fans was necessary, as well as data on the process intensities of the particular hazardous events. As a result, scatterplots were developed linking process intensities to object vulnerability values. These data were analysed using regression approaches in order to develop vulnerability functions, which served as a proxy for the structural resistance of buildings with respect to fluvial sediment transport processes on the fan of torrents.

2.3.1 Elements at risk

Elements at risk were defined as those dwelling houses of the settlements, which were located on the individual torrent fans. These were analysed in a spatially explicit way by using GIS. Following suggestions outlined in Kranewitter (2002) as well as Keiler et al. (2006b), values at risk were obtained by assigning values to these buildings; therefore, the reconstruction value was calculated for every individual element at risk within this study. This neglected any risk-dependent changes in the demand within the real estate market (Fuchs et al. 2007a). Furthermore, this value serves as a basis for the expressed preferences of the societal accepted value of protection against natural hazards in Austria (Fuchs et al. 2007b). The sets of calculation were based on the building size, and an average value applied by Austrian building insurers of € 1,670 per square metre was used as a basis for calculation. The building size was derived from digital cadastral maps (scale 1:1,000), which were provided by the respective local community administration. As the spatial quality and temporal actuality of the cadastral maps was found to be variable, particularly with respect to the number of storeys, the building height and the use of individual storeys as well as their state of repair, these data were updated by the interpretation of multi-temporal aerial photographs as well as field studies. The prices finally obtained represent reconstruction values of the individual buildings. Since residential property in the ground floor and in the first floor is more expensive than in cellars and attics, Eq. 1 was developed to take into account these differences accordingly. Furthermore, Eq. 1 acknowledges that due to the volume of interior walls the usable area for living has to be reduced by 10%.

$$ V = 0.9 \cdot A\{ U_{\text{A}} + U_{\text{C}} + n_{\text{S}} [U_{\text{L}} (1 - r)]\} $$
(1)

where V = value of the building; A = area of the building; n S = number of storeys; U = unit price; r = reduction factor for state of maintenance and interior conditions; the indices L, A and C stand for living space, attic and cellar.

Loss data were collected using information derived from the individual administrative bodies on the Austrian Länder level. Professional damage appraisers of these administrative bodies estimated the loss of any individual element at risk in monetary terms on an object level. Losses which can be attributed to the building envelope only were identified and prepared for the subsequent analysis. These monetary loss assessments were applied within this study for the calculation of the damage ratio of every individual element at risk, defined by the ratio between loss and reconstruction value.

2.3.2 Process intensity

The intensity of a process defines the impact and the effect on an element at risk, whereas in contrast the process magnitude is a measure for the size of the process (e.g., sediment volume). Since process magnitudes are often not directly measured during an event, the intensity is used instead in order to classify the size of a hazard. It is widely acknowledged that different processes and different process intensities lead to different vulnerabilities due to a different physical impact on the elements at risk. Depending on the natural phenomenon, different parameters are applicable for the development of vulnerability-intensity relationships, such as impact pressures and flow velocities.

The process characteristics of the studied events were determined by using information derived from process documentations, i.e., a documentation of deposition heights and flow depths. These documentations are regularly carried out subsequently after individual events by the Austrian Torrent and Avalanche Control Service. As a result, deposition heights were assigned to individual buildings in terms of a proxy for respective process intensities. The data set was supplemented by the analysis of data obtained from a nearest neighbourhood interpolation carried out in a GIS environment for those buildings that were not directly assessed during the field campaigns of the Austrian Torrent and Avalanche Control Service.

With respect to the derived process intensities, two complementary sets of calculation were subsequently carried out. First, the deposition height as an absolute intensity per building was used to attribute loss heights, which followed an approach recently outlined in Fuchs et al. (2007a) with respect to debris flows. Secondly, a relative intensity was calculated based on the observation that the cellar and ground floor of any exposed building is more susceptible to torrent processes than any other storey including the attic. Consequently, the vulnerability of large buildings would be over-estimated, and the vulnerability of small buildings would be under-estimated if the intensities were rated based on an absolute value, in particular for medium process intensities. Therefore, a normalised relative intensity I R was introduced, composed from a ratio between the deposition height I and the height of the affected building H (see Eq. 2).

$$ I_{\text{R}} = \frac{I}{H} $$
(2)

2.3.3 Loss functions

The derived scatterplots for vulnerability values, linking process intensities to individual degrees of loss, were analysed using regression approaches in order to develop vulnerability functions. The distributions had to comply with the mathematical requirements of:

  • defining vulnerability as the depending variable in a both-sided confined interval [0;1];

  • steady and monotonic increasing within the interval of its explaining variable (intensity);

  • steadiness with respect to higher orders within the defined interval; and

  • definition of its explaining variable either in a both-sided unconfined interval (−∞; +∞) or in a left-sided confined interval [0; +∞).

Theoretically, an infinite set of distributions would be possible to meet these requirements. An extensive description of available approaches and distributions is given in Plate (1993). Approaches used in extreme value statistics were considered; these were the Gumbel, Frechet, and Weibull distribution. Additionally, an exponential and a logistic distribution were tested. These distributions have the following characteristics: steadiness, a steady derivation is possible also in higher orders, and the dependent variable ranges in a both-sided confined interval [0;1]. At the same time, the explaining variable can range in a both-sided unconfined interval (−∞; +∞) or in a left-sided confined interval [0; +∞). In Table 3, possible distributions are summarised and their characteristics are outlined.

Table 3 General functional approaches for regression analysis of vulnerability
Full size table

The interval of the explaining variable of the functional approaches presented in Table 3 is generally defined as a both-sided unconfined interval (−∞; +∞), apart from the Frechet distribution, which shows a left-sided confined interval [0; +∞). As the intensity of any vulnerability function ranges from 0 to theoretically +∞, the functional approaches of Table 3 had to be modified to fit to the left-sided confined interval [0; +∞) of the explaining variable (intensity). Additionally, to introduce further parameters, a shift was inserted and scaled to fit in the left-sided confined interval [0; +∞). This mathematical operation increased the number of unknown and fittable parameters, which allowed a better fitting of the chosen approaches to the given data. Theoretically, an approach containing an infinite number of parameters will return the best-fitting function because the vector of unknown parameters can be optimised to maximise the coefficient of determination. The modified distributions, which were used in this study, are compiled in Table 4. To provide proper mathematical theory and to achieve better applicable functions for the modified Weibull distribution and the modified Frechet distribution, the number of unknown parameters was limited to a maximum of three parameters.

Table 4 Modified functional approaches for regression analysis of vulnerability
Full size table

The distributions shown in Table 4 were used for a parameter estimation procedure of the data. The used procedure of regression analysis and parameter estimation followed an approach in statistic analysis of extreme values and rare events (Plate 1993). As all the functions fulfil the necessary preconditions, the choice of the best-fitting function was made by analysing quantitative factors. Similar to an Analytic Hierarchy Process used for decision-making procedures or utility analysis (Saaty 1980), different factors were chosen to determine the applicability of the distributions. The sum of these factors represented a value of utility. The higher the value of utility of a certain distribution is, the better is the fitting behaviour of this distribution. The factors chosen were (1) the coefficient of determination; (2) the maximum upper residual and (3) the maximum lower residual. The residuals were included in the utility analysis to give consideration to the importance of the outliers during the parameter estimation procedure. Generally, all quantitative factors are weighted equally, while within this study more emphasis was given to the coefficient of determination. Hence, a weighting factor of 0.5 was assigned to the coefficient of determination, whereas a weighting factor of 0.25 was used both for the upper and for the lower residuals. The higher the coefficient of determination is, the higher its influence on the value of utility. The residuals, defined as the difference between the individual data point and the fitted function value, influence the value of utility in the opposite way. The smaller the residuals are, the better the applicability of the respective function (see Eq. 3).

$$ U = {\text{CD}} \cdot 0.5 + (1 - R_{\text{U}} ) \cdot 0.25 + (1 - \left| {R_{\text{L}} } \right|) \cdot 0.25 $$
(3)

where U = value of utility; CD = coefficient of determination; R U = maximum upper residual and R L = maximum lower residual.

As outlined earlier, relative intensity was introduced in this study as a normalised parameter. A relative intensity larger than the value of 1 would imply a burying of the building above the building size, which was excluded in this study due to missing observations with respect to torrent fans located in the European Alps. Therefore, it was assumed that the normalised relative intensity does not exceed the value of 1; consequently, the interval of absolute intensity changes from a left-sided confined interval [0; +∞) to a both-sided confined interval [0;1]. The interval of vulnerability [0;1]—as the dependent variable—remains unchanged. As the distributions presented in Table 4 were suitable for a left-sided confined interval [0; +∞) of the explaining variable, a transformation was needed if the normalised relative intensity was used. An appropriate method of transforming a variable defined in a left-sided confined interval [0; +∞) into a variable defined in a both-sided confined interval [0;1] is given by a tangent-transformation (Bronštejn et al. 2008). By substituting the term x in the distributions shown in Table 4 by the term tan(x · π/2), these distributions can equally be used for the description of normalised relative intensities.

2.3.4 Estimation of uncertainty

Confidence bands for different confidence levels are used in regression analysis to show the uncertainty inherent to regression functions. The confidence bands were calculated by using a linear transformation approach (Plate 1993). First, the best-fitting function for absolute as well as relative intensity was converted into a linear form (Eq. 4).

$$ y_{\text{trans}} = a_{\text{trans}} \cdot x + b_{\text{trans}} $$
(4)

The parameters a trans and b trans were calculated based on the exponents and factors of the original regression functions. The values for degree of loss and for intensity (absolute as well as relative) were transformed into the linear system.

Secondly, by means of these transformed values, intermediate values needed for the determination of the linear confidence bands (Q x , Q y , Q xy and s xy ) were calculated. Confidence bands with different confidence levels (90, 95 and 99%) were calculated based on quantile values of the t-distribution. The linear confidence bands were based on the following general form (Eq. 5):

$$ y_{\text{trans}}^{\text{u,l}} (x) = a_{\text{trans}} \cdot x + b_{\text{trans}} \pm t_{{1 - {\frac{\alpha }{2}};n - 2}} \cdot s_{xy} \cdot \sqrt {\frac{1}{n} + {\frac{{(x - \bar{x}_{\text{trans}} )^{2} }}{{Q_{x} }}}} $$
(5)

where y u,ltrans  = upper and lower confidence value of the linear function at the location x; t = t-distribution value with α level of significance and n degrees of freedom and \( \bar{x}_{\text{trans}} \) = arithmetic mean of the transformed intensity value.

Thirdly, the linear confidence bands were transformed back to fit to the original regression functions. The back-transformation was conducted for absolute intensity by applying Eq. 6a and, in case of relative intensity, by applying Eq. 6b.

$$ y_{\text{u,l}}^{\alpha } (x) = 1 - {\text{e}}^{{ - {\text{e}}^{{y_{\text{trans}}^{\text{u,l}} ({ \ln }x)}} }} $$
(6a)
$$ y_{\text{u,l}}^{\alpha } (x) = {\text{e}}^{{ - {\text{e}}^{{y_{\text{trans}}^{\text{u,l}} \left( {\ln \left( {{ \tan }\left( {{\frac{x \cdot \pi }{2}}} \right)} \right)} \right)}} }} $$
(6b)

where y αu,l  = upper and lower confidence value of the original regression function at the location x.

3 Results

In total, 116 buildings were damaged in the three test sites due to the studied events. Since the focus of this study was on the development of a vulnerability function for residential buildings, the 67 dwelling houses situated on the individual torrent fans were assessed (Table 5).

Table 5 Number of damaged buildings and number of buildings considered in this study for each test site
Full size table

The total damage of the considered houses amounted to approximately € 5.5 million. The total amount of reconstruction values according to the procedure used by the Austrian insurance business was equal to € 37.6 million. Due to the different intensities, the severity of damage varies considerable. The individual loss amounted from € 438 to € 828,240. Because of different building sizes, the reconstruction values showed a wide range from about € 221,000 to € 1.34 million. These variations lead to individual vulnerabilities ranging from 0.001 to 1.0. The mean vulnerability per exposed building is equal to 0.168. In Table 6, damage and property values, the range of vulnerability and the mean vulnerability per exposed residential building for the individual test sites are shown.

Table 6 Reported loss, property value, range of vulnerability and mean vulnerability for each test site
Full size table

In Figs. 5 and 6, the vulnerability relation for detached dwelling houses is shown, based on absolute deposition heights (Fig. 5a) and relative intensity (Fig. 6a) as proxies for process intensities in the affected area. The process intensity is plotted on the abscissa, and the degree of loss is plotted on the ordinate. In general, vulnerability increases with increasing intensity. In both figures, the shape of the Weibull, Frechet and Logistic distributions is similar. For low process intensities (I < 1 m for absolute intensities and I R < 0.1 for relative intensities), these distributions show a slow increase in vulnerability. For medium process intensities (1 m ≤ I ≤ 2.5 m for absolute intensities and 0.1 ≤ I R ≤ 0.3 for relative intensities), the highest rate of increase in vulnerability is observed, following an almost linear curve. For high process intensities (I > 2.5 m for absolute intensities and I R > 0.3 for relative intensities), the observed rate of increase in vulnerability slows down again and the curves converge towards 1. Due to these specific shapes, the effect of an increase in process intensity is different in the three sections of these curves; an increase in process intensity of 0.5 m causes as such more additional damage at medium intensities compared to low and high intensities. A deviation from this pattern is observed for the exponential curve, given the nature of this distribution.

Fig. 5
figure 5

Different vulnerability functions for dwelling houses based on deposition height as a proxy for the process intensity. Vulnerability values originating from the study sites are indicated by dots. The best-fitting function to describe the range in the analysed data (highest value of utility; Weibull) is highlighted in bold (a). Confidence bands for different confidence levels (CL = 90, 95 and 99%) for the best-fitting function (b)

Full size image
Fig. 6
figure 6

Different vulnerability functions for dwelling houses based on relative intensity. Vulnerability values originating from the study sites are indicated by dots. The best-fitting function to describe the range in the analysed data (highest value of utility; Frechet no. 2) is highlighted in bold (a). Confidence bands for different confidence levels (CL = 90, 95 and 99%) for the best-fitting function (b)

Full size image

In Fig. 5a, the distributions for absolute process intensities are shown, which are grouped in steps of 0.25 and 0.5 m, respectively. Mainly in the process intensity categories of 1.0 and 1.5 m, the statistical spread of the vulnerability values is considerable, which can be attributed to a possible intrusion of material through building openings (Fuchs et al. 2007a). As windowsills are generally situated at a height of approximately 1.0 m, the quality of the windows, their location regarding the main impact direction and the impact force of the process define whether or not the interior of the building is harmed. The best-fitting function to describe the range in the analysed data (highest value of utility) was the modified Weibull distribution (see Eq. 7), which is highlighted in Fig. 5a. Their value of utility equals 0.792 while the coefficient of determination is equal to 0.914.

$$ V_{\text{E}} = 1 - {\text{e}}^{{ - 0.443\left( {{\frac{I + 1.442}{1.442}} - 1} \right)^{2.233} }} $$
(7)

In Table 7, the mathematical notation (where, V E = economic vulnerability and I = absolute intensity), the coefficient of determination, the maximum upper and lower residual and the value of utility of the distributions based on absolute intensity are summarised.

Table 7 Compilation of the applied distributions based on deposition height as a proxy for the absolute process intensity
Full size table

To take into account different building heights, a normalisation of the intensity parameter was applied. This was done by changing the intensity parameter from absolute to relative values. Relative intensity values were derived by relating the deposition values to individual building heights. In Fig. 6a, the considered distributions are shown. The best-fitting function to describe the range in the analysed data (highest value of utility) was the modified Frechet distribution no. 2 (see Eq. 8), which is highlighted in Fig. 6a. Their value of utility equals 0.838 while the coefficient of determination is equal to 0.958.

$$ V_{\text{E}} = {\text{e}}^{{ - 0.466\left( {{\frac{{\tan \left( {{\frac{{I_{\text{R}} \cdot \pi }}{2}}} \right) + 0.395}}{0.395}} - 1} \right)^{ - 2.091} }} $$
(8)

In Table 8, the mathematical notation (where, V E = economic vulnerability and I R = relative intensity), the coefficient of determination, the maximum upper and lower residual and the value of utility of the distributions based on relative intensity are summarised.

Table 8 Compilation of considered distributions based on relative intensity values
Full size table

In Figs. 5b and 6b, the confidence bands of the best-fitting functions (Weibull distribution in case of absolute intensity and Frechet distribution no. 2 for relative intensity) are shown for different confidence levels. The process intensity is plotted on the abscissa, and the degree of loss is plotted on the ordinate. In general, the confidence bands show a similar shape as the best-fitting functions they are related to. The width of the confidence bands reaches a maximum for medium process intensities due to both the statistical spread of the original data and the generally limited number of data points in this intensity range. The confidence bands converge towards 1 for high process intensities.

When comparing the results obtained by taking absolute and relative values for process intensities, a slightly higher correlation with respect to the latter method becomes obvious (R 2 = 0.914 vs. 0.958). Therefore, the use of relative intensity instead of absolute intensity may be suggested, since an improvement in the mathematical model describing regression between intensity and degree of loss was observed.

4 Discussion and conclusion

Within the framework of the presented study, an empirical vulnerability function was developed for buildings located on alpine torrent fans and which are prone to torrent processes, i.e., fluvial sediment transport. The vulnerability function presented refers to the physical susceptibility of buildings and was based on an economic approach linking object-based loss data to reconstruction values. Thus, the proposed vulnerability function may be used in operational risk analyses for torrent hazards, particularly since the approach is suitable for a spatially explicit valuation within a GIS environment.

The analysis was conducted on a local scale based on data analyses for three Austrian test sites. The results had shown that the application of relative intensity values resulted in an increased coefficient of determination compared to the function based on absolute intensities. In general, the best-fitting functions were reliable with respect to an increase in vulnerability if the process intensity increased. In detail, the data did not suggest a linear increase since the highest rates in increase in vulnerability were observed for medium process intensities. Compared to the second order polynomial functions applied by Fuchs et al. (2007a) and Akbas et al. (2009) for debris flows, or linear functions as outlined in Barbolini et al. (2004) with respect to snow avalanches, the probability functions presented in this study seem to be more reliable due to the methodological constraint that physical vulnerability ranges between 0 and 1 (e.g., Varnes 1984). Regarding the selection procedure of the best-fitting function, three factors (coefficient of determination, the maximum upper residual and the maximum lower residual) were included in this study. However, a consideration of further factors to calculate the value of utility may improve the results. The median and mean of the residuals derived from a residual analysis could be such factors.

The results of this study showed that fluvial sediment transport processes due to torrent events cause similar economic damage than data related to debris flow processes (Fuchs et al. 2007a; Akbas et al. 2009). Hence, the general assumption that fluvial sediment transport processes are less destructive than debris flow processes (Hungr et al. 2001) cannot be confirmed for torrent processes in Austria.

It has been shown that the normalisation of the process intensity considerably improved the calculations. Therefore, the normalisation of intensity seems to be a promising step towards quantitative risk analysis. However, the normalisation was carried out under the assumption that buildings are buried only until a maximum which equals the building height (intensity range between 0 and 1). Consequently for a relative intensity value of 1, a complete destruction of the building is implied (Table 9). In contrast, if the calculation is based on absolute intensities, the intensity represents an infinite value. From a mathematical point of view, only intensities equal to ∞ result in a vulnerability value of 1, whereas the considered torrent events had shown that a destruction of buildings can be already observed at process intensities of 2.5–3.0 m (see Table 9; Fig. 5a).

Table 9 Summary of vulnerability values for the modified Weibull distribution (absolute intensities) and the modified Frechet distribution no. 2 (relative intensities)
Full size table

Physical susceptibility of elements at risk and thus vulnerability is strongly dependent on the construction material used. The developed vulnerability functions are applicable to buildings, which are constructed by using brick masonry and concrete, a typical design in post-1950s building craft in Alpine countries. Consequently, the adjusted functions may be applicable to this mixed construction type if residential buildings are assessed during risk analyses. However, a wider application of the presented approach to additional building categories such as hotels or business establishments is still outstanding.

Although significant advancements have been made in risk research, especially with respect to the conceptualisation and representation of vulnerability within the human–environment system (Turner II et al. 2003; Adger 2006; Cutter 2006; Eakin and Luers 2006; Folke 2006), considerable differences in the definition of vulnerability within the research community remain. These differences are rooted in a different understanding of the definition and conceptualisation of vulnerability in the domain of social sciences and of natural sciences.

With respect to mountain hazards, it has been argued that there is neither a common definition nor theory developed on how to assess vulnerability—despite the premise that vulnerability is driven by exposure, resistance and resilience (cf. Fuchs 2009). In social sciences, vulnerability is conceptualised as a set of socio-economic factors that determine an individual’s or a societal ability to cope with stress or perturbation.Footnote 3 In natural sciences, vulnerability is understood in terms of the expected degree of damage and the associated height of loss for a given element at risk within a specific timeframe.

In order to overcome this conceptual separation, and based on studies carried out in the eastern Alps, an integrative model that allows for a comprehensive representation of vulnerability has been proposed by Fuchs (2009). The underlying idea of taking such an integrative viewpoint was the cognition that human action in mountain environments affects the state of vulnerability, and the state of vulnerability in turn shapes the possibilities of human action. Hence, the vulnerability of a specific location and within a considered point of time is triggered by the hazardous event and the related physical susceptibility of structures, such as buildings located on a torrent fan (physical vulnerability).

Depending on the specific institutional settings, economic vulnerability of individuals or of the society results, above all with respect to imperfect loss compensation mechanisms in the areas under investigation (Holub and Fuchs 2009). While this potential for harm can be addressed as social vulnerability, the concept of institutional vulnerability has been developed with respect to the overall political settings of governmental risk management. As a result, the concept of vulnerability, as being used in natural sciences, can be extended by integration of possible reasons why such physical susceptibility of structures exists and by integration of compensation mechanisms and coping strategies being developed within social sciences.

Consequently, in some decision contexts one approach to reduce vulnerability is likely to be more effective than another, whereas in other situations a combination may also be appropriate. To give an example, for some buildings located on torrent fans local structural mitigation (e.g., splitting wedges) to be born by the homeowner will be the most promising (and cost-effective) measure to reduce damage, while for other buildings and given another topographic setting the provision of risk sharing mechanisms by obligatory insurance solutions will be most efficient. Often a combination of both will be more successful in reducing the individual and collective risk than only one mitigation alternative (Fuchs et al. 2007b). Effective planning for and response to hazards requires that the vulnerability associated with specific social and decision processes be understood in parallel with understandings of probabilities of occurrence leading to physical vulnerability. Thus, judgements can be made about the appropriate balance between different management options.

Apart from these conceptual issues, a deeper insight into structural vulnerability was gained during the attempt to develop an empirical vulnerability function for use in risk assessment for alpine torrents and to supplement studies related to debris flows (Fuchs et al. 2007a) by studies on processes characterised by fluvial sediment transport. This attempt was based on the realisation of a specific research gap with respect to mountain hazards in Europe. So far, structural vulnerability had only been quantified insufficiently regarding the requirements of operational risk analyses. As a result, a general strategy in determining vulnerability of elements at risk to specific events was still missing since vulnerability models were mainly based on plausibility issues, expert knowledge, conceptual approaches, and assessments of historical data. The method presented followed a spatial approach and was based on process intensities, the spatial characteristics of elements at risk and average reconstruction values on a local scale. Since vulnerability was defined using an economic approach, the relation between reconstruction values and losses principally allows a wider application in regions with different economic background and on different spatial scales.

Future needs concerning vulnerability research might include the temporal changes in vulnerability to natural hazards. During the past decades, European mountain regions experienced major transformations in population size, economic conditions, social characteristics and development patterns. As a result of the discussed evolution in socio-economic activity, and an associated relative increase in individual assets, vulnerability might have changed considerably (Fuchs et al. 2005; Keiler et al. 2006a). To improve natural hazard risk management, these changes should be quantified according to arising institutional, economic and social implications.

Apart from such academic concerns, methods to reduce vulnerability to natural hazards may include innovative approaches of risk sharing, as discussed in Holub and Fuchs (2009). These approaches are pillared by a mandatory insurance system against natural hazards, based on premiums which are commensurate with the risk. Therefore, legislation, loss compensation and risk transfer are accompanied by the overall aim to increase risk awareness and to implement a sustainable and long-term land use planning. In order to achieve this goal, information on hazard and risk at a specific location should be communicated in a target-oriented way to the stakeholders involved in order to create risk awareness and to provide incentives for vulnerability-reducing behaviour. It has been shown by Fuchs et al. (2009) how standardised guidelines for the visual representation of risk will meet these goals and therefore improve the dissemination of information accordingly. As a result, overall vulnerability to mountain hazards may decrease in the future.