Application of bivariate extreme value distribution to flood frequency analysis: a case study of Northwestern Mexico

Abstract

In Mexico, poverty has forced people to live almost on the water of rivers. This situation along with the occurrence of floods is a serious problem for the local governments. In order to protect their lives and goods, it is very important to account with a mathematical tool that may reduce the uncertainties in computing the design events for different return periods.

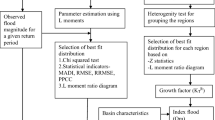
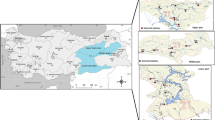
In this paper, the Logistic model for bivariate extreme value distribution with Weibull-2 and Mixed Weibull marginals is proposed for the case of flood frequency analysis. A procedure to estimate their parameters based on the maximum likelihood method is developed. A region in Northwestern Mexico with 16 gauging stations has been selected to apply the model and regional at-site quantiles were estimated. A significant improvement occurs, measured through the use of a goodness-of-fit test, when parameters are estimated using the bivariate distribution instead of its univariate counterpart. Results suggest that it is very important to consider the Mixed Weibull distribution and its bivariate option when analyzing floods generated by a␣mixture of two populations.

Appendices

Appendix A: Weibull-2 and Mixed Weibull distributions

The cumulative Weibull distribution function with two parameters is

$$ F{\left(x\right)} = 1 - \exp ^{{-{\left({\frac{x} {\alpha}} \right)}}^{\beta}}\quad x\geq0,\alpha{\hbox{ and }}\beta\geq0 $$

(4)

where α and β are the scale and shape parameters.

The probability density function is given by

$$ f{\left(x\right)} = \frac{\beta} {\alpha }{\left({\frac{x} {\alpha }}\right)}^{{\beta - 1}} \exp ^{{- {\left({\frac{x} {\alpha}} \right)}}^{\beta}} $$

(5)

Parameters can be estimated by the direct maximization of equation (6)

$$ \ln L = \ln {\prod\limits_{i = 1}^n {f{\left({x_{i} ;\alpha, \beta} \right)}}} $$

(6)

where L is called the likelihood function, ln is the natural logarithm, α, β are the parameters to be estimated, and n is the length of record.

In flood frequency analysis, whenever the return period T is large compared with the length n of the available series, the error in the T-year flood estimate is greatly affected by the flood distribution model adopted. Difficulties are met in selecting a theoretical flood distribution mainly from the fact that in many sites some of the annual flood series exhibit one or more values ranking much higher than the bulk of the remaining data. Extreme events that are shown to be very unlikely to occur in a sample are called outliers.

The use of a mixture of probability distributions functions for modeling samples of data coming from two populations have been proposed long time ago (Mood et al. 1974):

$$ \Pr {\left({X \leq x}\right)} = F{\left(x\right)} = pF_{1} {\left(x\right)} + {\left({1 - p}\right)}F_{2} {\left(x\right)} $$

(7)

where p is the proportion of x in the mixture and F(x) is said to be a mixture of distributions.

If two component are Weibull distributions with two parameters, equation (4) yields to the five-parameter mixture model of annual floods:

$$ F{\left(x\right)} = p{\left[{1 - \exp ^{{ - {\left({\frac{x} {{\alpha_{1}}}}\right)}}^{{\beta_{1}}}}}\right]} + {\left({1 - p}\right)}{\left[{1 - \exp ^{{ - {\left({\frac{x} {{\alpha_{2} }}}\right)}} ^{{\beta_{2}}}}}\right]} $$

(8)

where α₁ , β₁ and α₂, β₂ are the scale and shape parameters for the first and second population, respectively, and p is the association parameter (0 < p < 1).

The corresponding probability density function is

$$ f{\left(x\right)} = p\frac{{\beta_{1}}} {{\alpha_{1}}}{\left({\frac{x} {{\alpha_{1}}}}\right)}^{{\beta_{1} - 1}} \exp ^{{-{\left({\frac{x} {{\alpha_{1}}}}\right)}} ^{{\beta_{1}}}} +\ {\left({1 - p}\right)}\frac{{\beta_{2}}} {{\alpha_{2} }}{\left({\frac{x} {{\alpha_{2}}}}\right)}^{{\beta_{2} - 1}} \exp^{{ - {\left({\frac{x} {{\alpha_{2}}}}\right)}} ^{{\beta _{2}}}} $$

(9)

Parameters can be estimated by the direct maximization of equation (10)

$$ \ln L = \ln {\prod\limits_{i = 1}^n {f{\left({x_{i} ;\alpha_{1} ,\beta_{1} ,\alpha_{2} ,\beta_{2} ,p}\right)}} } $$

(10)

Appendix B: maximum likelihood procedure

The general form of the bivariate likelihood function is Raynal (1985):

$$ L{\left({x,y,\underline{\theta}}\right)} = {\left[{{\prod\limits_{i = 1}^{n_{1} } {f{\left({r_{i} ,\underline{\theta}_{1} }\right)}}}}\right]}^{{I_{1}}} {\left[{{\prod\limits_{i = 1}^{n_{2} } {f{\left({x_{i} ,y_{i} ,\underline{\theta}_{2}} \right)}}}}\right]}^{{I_{2}}} {\left[{{\prod\limits_{i =1}^{n_{3}} {f{\left({s_{i} ,\underline{\theta}_{3} }\right)}} }}\right]}^{{I_{3}}} $$

(11)

where n ₁ is the length of record before the common period, n ₃ is the length of record after the common period, n ₂ is the length of record in the common period, r is the variable with length n ₁, x,y are the variables with length n ₂, s is the variable with length n ₃ and I _i is a indicator number such that I _i  = 1 if n _i  > 0 or I _i  =  0 if n _i  =  0.

And its log-likelihood function is

$$ {\hbox{ln}}\  L{\left({x,y,\underline{\theta}}\right)} = I_{1} {\left[{{\sum\limits_{i = 1}^{n_{{_{1}}} } {{\hbox{ln}}\  f{\left({r_{i},\underline{\theta}_{1}}\right)}}}}\right]} + I_{{\hbox{2}}} {\left[{{\sum\limits_{{\hbox{i}} = {\hbox{1}}}^{n_{2} } {{\hbox{ln}}\  f{\left({x_{i} ,y_{i} ,\underline{\theta}_{2} } \right)}}}}\right]} + I_{3} {\left[{{\sum\limits_{i = 1}^{{{n}}_{{{\rm 3}}} } {{\hbox{ln }}f{\left({s_{i} ,\underline{\theta}_{3}}\right)}}}}\right]} $$

(12)

Due the complexity of the mathematical expressions in equation (12) and the partial derivatives with respect to the parameters, the constrained multivariable Rosenbrock method (Kuester and Mize 1973) was applied to obtain the estimators of the parameters by the direct maximization of equation (12).

In any of the multivariable constrained non-linear optimization techniques, global optimality is never assured. Therefore, care must be taken in order to avoid a local optimum. It is suggested to start always with the parameters computed through the univariate maximum likelihood approach by fitting the univariate distribution to the data of the gauging stations to be analyzed. So, initial parameters of marginal distributions are obtained by using the same optimization algorithm, maximizing equation (6) or (10), depending on selected model.