Heuristic Methods for Minimum-Cost Pipeline Network Design – a Node Valency Transfer Metaheuristic

Abstract

Designing low-cost network layouts is an essential step in planning linked infrastructure. For the case of capacitated trees, such as oil or gas pipeline networks, the cost is usually a function of both pipeline diameter (i.e. ability to carry flow or transferred capacity) and pipeline length. Even for the case of incompressible, steady flow, minimizing cost becomes particularly difficult as network topology itself dictates local flow material balances, rendering the optimization space non-linear. The combinatorial nature of potential trees requires the use of graph optimization heuristics to achieve good solutions in reasonable time. In this work we perform a comparison of known literature network optimization heuristics and metaheuristics for finding minimum-cost capacitated trees without Steiner nodes, and propose novel algorithms, including a metaheuristic based on transferring edges of high valency nodes. Our metaheuristic achieves performance above similar algorithms studied, especially for larger graphs, usually producing a significantly higher proportion of optimal solutions, while remaining in line with time-complexity of algorithms found in the literature. Data points for graph node positions and capacities are first randomly generated, and secondly obtained from the German emissions trading CO₂ source registry. As political will for applications and storage for hard-to-abate industry CO₂ emissions is growing, efficient network design methods become relevant for new large-scale CO₂ pipeline networks.

1 Introduction

1.1 Context

Network design problems arise in a multitude of scenarios. For fluid transport problems, such as oil or gas pipeline networks, the aim is to link all fixed points of the network via pipelines while matching fluid supply to demand and minimizing a defined cost-function. While historical gas distribution network layouts are created iteratively as new nodes are added, often resulting in suboptimal network designs, network layouts can be designed from scratch as new incentives or legislative restrictions arise. Networks that re-purpose and collect previously unused fluid commodity sources, such as industry CO₂ emissions (van den Broek et al. 2009; Alhajaj and Shah 2020) or slurry from dairy plants (Bietresato et al. 2013) all undergo a step of network design. Oppositely, networks that distribute a new commodity to a series of known recipients such as Hydrogen (André et al. 2013) or biogas networks (Heijnen et al. 2020), will nonetheless use an identical design process. All cases involve linking a series of fixed sources/sinks points via pipelines with associated capacity and cost. Although these cases are functionally identical, for clarity we consider here the multi-source, single-sink case that is local CO₂ collection networks. Furthermore, the methods studied here are applicable to multi-source, multi-sink scenarios, as long as sink and source capacities are defined, and total source and sink capacity match.

1.2 Problem Boundaries

Within this paper, we compare and propose graph-based heuristics to achieve minimum-cost pipeline network layouts. We therefore use a graph representation of physical networks. Fixed source locations are described by graph nodes which possess a fixed source capacity. Flow is used interchangeably here with the term capacity. The connections between the nodes, or edges, represent the pipelines that can connect either sources together, cumulatively adding capacity, or connect to a singular sink and discharge their capacity. Only trees, graphs without cycles, are considered here. Such single sink applications could include storage of German CO₂ emissions in a unique North Sea storage site, or alternatively, a regional CO₂ storage network with one storage location.

Network costs are given by the sum of individual pipeline costs. Pipeline cost functions per unit length are often given as quadratic functions of pipeline diameter D. As we assume steady, incompressible, frictionless flow in circular pipelines, D is therefore proportional to the square root of flow quantity. For H₂ (André et al. 2013) and CO₂ (Kazmierczak et al. 2009) networks, the pipeline cost dependence to capacity can be approximated by a constant exponent of 0.6, while for water networks it is closer to 0.7 (Heijnen et al. 2020). Brimberg et al. (2003) uses a constant exponent of 0.75 for an oil pipeline problem. In every case, the relative pipeline cost is expected to flatten with increasing flow, i.e., considering the economy of scale, a concave cost function of the transferred capacity is used.

The minimum-cost tree linking all elements of the network and respecting flow requirements, is known as the Minimum-cost Capacitated Spanning Trees problem (MCST). Finding capacity-free Minimum-cost Spanning Trees (MST) is solvable in polynomial time with methods such as Kruskal’s (1956) algorithm, where only network length is minimized. The addition of the capacity constraint adds computational complexity, as the attribution of capacity (and therefore cost) to each pipeline will depend on the exact network topology chosen, creating a highly non-linear optimization space. Switching a single edge may alter all the transferred capacities of the network, significantly altering the cost. As a result, local minima are easy to find and discovering the optimal MSCT may require iterating over all trees, attributing capacity, then calculating associated cost. The combinatorial nature of trees renders this problem NP-hard.

Steiner nodes are not considered in this study. The further addition of intermediate relay nodes, or Steiner nodes, to the network is expected to reduce overall costs. Steiner nodes do not require any capacity addition to the pipelines and simply provide a way of reducing the overall pipeline length. We limit the scope of our work here by not considering the addition of Steiner nodes and focus instead on finding low-cost MCSTs. While solutions to iteratively grow minimum-cost trees that include Steiner nodes do exist (Xue et al. 1999), Steiner nodes can also be added at opportune locations of a final MCST in a secondary step. In this regard, it has been recently shown (Heijnen et al. 2020) that the cost of the initial MCST will affect the cost of the MCST with added Steiner nodes, with lower final costs for lower-cost input MCSTs.

Supplementary pressure requirements on physical pipeline networks have been subject to extensive research as multiple constraints can be added on top of simple material balance through pipelines. Maximal pressure limitations for safe use, minimal pressure for ease of transport (e.g. supercritical CO₂), or limited commercially available pipeline diameters may exclude certain pipeline layouts. However, optimization of pipeline diameters is usually performed once an initial pipeline layout is set (Hansen et al. 1991; Robinius et al. 2019). Similarly, accounting for pressure losses through optimal compressor placement is dealt with at a later step in the overall cost optimization process (Mak et al. 2019; Elegancy 2020). We therefore leave out pressure considerations in the current work and focus on minimizing layout cost for continuous pipeline sizing.

1.3 Technical Background

Cayley’s (1857) formula shows that n^n − 2 spanning trees exist for n network nodes. Brute force iteration over all possible spanning trees to find the optimal MCST rapidly becomes impractical. Instead, graph optimization schemes are used to achieve low-cost trees rapidly. Mixed-Integer Programming makes use of traditional solver tools from mathematical programming and optimization (van den Broek et al. 2009; Brimberg et al. 2003; Sun and Chen 2016), and can provide exact solutions when computationally feasible. Elsewhere, agent-based methods such as Ant Colony Optimization (Maier et al. 2003) or Particle Swarm Optimization (Liu et al. 2016) start from different initial solutions and attempt to converge cooperatively towards a minimal-cost network. All these methods can benefit from graph-based heuristic algorithms along the way, as they provide quick, good results when an optimal solution is not required at that point.

A graph-based heuristic algorithm will locally modify a starting solution until no further improvement can be found. As well standalone use, they are usually employed for two specific reasons: first as initial requirement of a good starting solution for other methods, typically as an upper bound for exact methods such and Branch-and-Bound(Lawler and Wood 1966; Brimberg et al. 2003), and secondly at intermediate steps in wider metaheuristic methods. For both uses, higher performance is measured by shorter calculation times and lower solution cost. Graph-based heuristic algorithms are numerous (Kazmierczak et al. 2009; Bietresato et al. 2013; André et al. 2013; Heijnen et al. 2020) and performance trade-offs between calculation time and lower cost are chosen depending on use. In the case of exact Branch-and-Bound methods, obtaining a close-to-optimal upper bound from a heuristic can vastly decrease calculation time by reduction of the search tree size (Morrison et al. 2016).

The conceptual simplicity of graph-based heuristic methods also makes them attractive to decision makers and stakeholders alike and allows easy modification to integrate extra system requirements. For example, pipeline transport might be prohibited through certain areas (e.g. natural parks) (Richardson et al. 2017), or encouraged through other areas (e.g. existing pipeline corridors) (Reuß et al. 2019). Modification of the cost of selected network links can be done accordingly (Yeates et al. 2020).

1.4 Contribution

Given the numerous occurrences of graph-based heuristic algorithms in pipeline layout design, we dedicate our study to comparing and improving the state-of-the-art, aiming for heuristics that are both better performing and reasonably fast. We make three distinct contributions in our work. First, we establish a baseline of MCST heuristic algorithms with associated performance statistics. The problem is applied to the case of pipeline layout design through a relevant pipeline cost function. A similar comparison is done in the work of Brimberg et al. 2003, but we include more recent algorithms and make some small extensions on literature algorithms. Secondly, we present an original metaheuristic based on identifying and transferring the edges specifically of high valency nodes. This metaheuristic performs very well, both reaching high proportions of optimal solutions within reasonable timescales. To enhance performance, we compare the use of the metaheuristic in combination with various lower-level heuristics, some specifically designed for the case. We conclude that a poorly performing (but fast) steepest-descent lower-level heuristic used in combination with the proposed metaheuristic still largely finds the same final solutions than a better performing (but slower) one. This grants a reduction in overall calculation time. The third contribution is the proposal of CO₂ collection networks based on real world data from the European Trading Scheme registry. The German CO₂ networks represent a case study for industry source CO₂ collection in future emission landscape. The CO₂ sources exclude emissions originating from energy generation due to the ongoing phase-out of coal industry in Germany and the rapid transition to renewable energy.

1.5 Outline

In a first step we give a non-exhaustive review of some applicable pipeline layout heuristics and metaheuristics and introduce some of our own. Heijnen et al. (2020) do a more comprehensive comparison of algorithms, but here we only pick the best performing, with some additions from our own literature review. To do so, we make use of discrete optimization terms and concepts. At the same time, we describe the concepts and algorithms in an accessible way that can be understood by scientists and stakeholders in network design alike.

In a second step, we apply the algorithms directly to a series of networks with differing numbers of graph nodes, comparing the minimum-cost network found for each algorithm with an optimal solution, when possible. After providing some performance statistics based on a random generation of data points, one-to-one algorithm comparison results are given using existing clusters of CO₂ industry emission sources in Germany provided by the European Emissions Trading Scheme (ETS) data (German Environment Federal Office 2019).

2 Materials and Methods

2.1 Problem Definition

We give a mathematical formulation of the problem to solve, similar to formulations presented in De Wolf and Smeers (1996) and Heijnen et al. (2020).

Let N = [N₁, N₂,…, N_n] be a list of nodes on known locations in the 2D Euclidean plane, each with a constant known capacity C = [C₁, C₂,…, C_n]. Corresponding node positions are given by P = [P₁, P₂,…, P_n]. The subset of source nodes N_s furthermore all have positive capacity. The subset of sink nodes N_D have negative capacity. Here N_D comprises a single sink D which collects the network capacity from the all the source nodes, therefore N_D = [D]. To ensure overall network material balance, the sink takes a capacity value C_D given by the opposite of the aggregate capacity of the sources (Eq. 1):

$$ {C}_D=-{\sum}_{m\in {N}_s}{C}_m $$

(1)

E(T) is the set of edges within the network T. As only trees are considered here, there is a unique flow direction along each edge. The flow direction along an edge e_ij from nodes i to j is then denoted (i, j), whereas non-directional quantities between nodes such as length and cost are denoted as ij.

An edge e_ij possesses a cost which is a combined function of the edge length l_ij and transferred capacity in the edge q_(i, j). The cost of the edge e_ij is then given by (Eq. 2):

$$ Cost\left({e}_{ij}\right)={l}_{ij}{q_{\left(i,j\right)}}^{0.6} $$

(2)

This pipeline cost function is a reasonable approximation for CO₂ pipelines (Kazmierczak et al. 2009; Heijnen et al. 2020). The cost of the network T formed by the edges is then given by the sum of all pipeline costs (Eq. 3):

$$ Cost(T)=\sum \limits_{\forall i,j\in E(T)} Cost\left({e}_{ij}\right)=\sum \limits_{\forall i,j\in E(T)}{l}_{ij}{q_{\left(i,j\right)}}^{0.6} $$

(3)

Source nodes can output their own capacity as well as transmit capacity from other source nodes. Therefore, equation Eq. 4 applies for any node n within the set N_s:

$$ \sum \limits_{\forall i,n\in E(T)}{q}_{\left(i,n\right)}-\sum \limits_{\forall n,i\in E(T)}{q}_{\left(n,i\right)}={C}_n $$

(4)

Furthermore, a sink can only take a role as a demand node and has no flow output. Therefore, coherent with Eq. 1, for the sink node D we obtain (Eq.5):

$$ \sum \limits_{\forall i,D\in E(T)}{q}_{\left(i,D\right)}=-{C}_D $$

(5)

The problem consists of finding the minimum-cost network according to Eq. 3 that respects the constraints given in Eq.4–5.

2.2 General Procedure

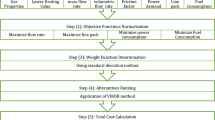
The general strategy we use to obtain a Minimum-cost Capacitated Spanning Tree is given in Fig. 1. This overall procedure was also used by Yeates et al. (2020) and Heijnen et al. (2020), but in this case we make use of different and original network optimization algorithms (heuristics and metaheuristics) in the key the final step. A series of sources are initially connected by the Minimum Spanning Tree (MST) to a chosen sink. Capacity is then uniquely attributed to the edges. This is calculated using the capacity allocation procedure proposed by Heijnen et al. (2020). The capacity allocation for a given network layout and with a complementary total sink-source capacity (Eq. 1) is proven to be unique by Robinius et al. (2019). The location of the sink is chosen either randomly, along with the positions and flow requirements of the sources (Section 3.1), or as a set of multiple positions in a regular grid surrounding the sources (Section 3.2). The initial capacitated tree given by the MST layout then serves as starting point for the heuristics and metaheuristics explored in the “Network optimization” step shown in Fig. 1.

Fig. 1

Procedure for finding a minimum-cost network. Sources are shown in red, while the sink is shown in purple. Using opposite capacity requirements on the sources and sink yields the equivalent problem

Optimal configurations of networks are sensitive to the exact exponent used in Eq. 2. The methods in this paper are applicable to any exponent between 0 and 1. These two limiting scenarios serve to illustrate the influence of the exponent. For a capacity exponent of 0, capacity no longer contributes to the pipeline cost, and the optimal tree simply minimizes total pipeline length, given by the MST. Oppositely, for a capacity exponent of 1, the incentive to join flow in larger capacity pipelines no longer exists. Two parallel pipelines cost as much as a single pipeline of combined flow. In this situation, each source then has its own direct pipeline to the sink, creating a hub network (Heijnen et al. 2020). The lowest-cost networks for intermediate exponent values in between 0 and 1 therefore represent the best combined trade-off between overall pipeline length reduction and joining of pipelines into higher capacity, comparatively lower-cost pipes. Note that for higher capacity exponents than explored here, a better starting point for optimization heuristics (Fig. 1) might be the hub network, with all sources directly connected to the sink, rather than the MST (Heijnen et al. 2020).

2.3 Algorithms

In this section we provide a series of literature heuristics and metaheuristics and supplement them with our original proposals. As seen in Fig. 1, a network optimization algorithm (last two tiles in Fig. 1) attempts to find lower-cost capacitated trees through modifications of the tree topology (i.e. modification of pipeline network layout), adaptation of the edge capacity (i.e. pipeline flow) requirements where needed, and recalculation of cost. Topology modifications typically involve breaking the tree at an existing edge and recombining the two disconnected parts of the initial tree via a previously unconsidered edge. These transformations can be described by a formal distance metric, a measure of difference between solutions, most simply given as a function of the symmetric difference between the sets of edges. The distance metric d₁ between two solution networks T1 and T2 is here given by half the number of elements in the symmetric difference between sets of edges E(T1) and E(T2), shown in (Eq. 6).

$$ {d}_1\left(T1,T2\right)=\left|E(T1)\triangle E(T2)\right|/2 $$

(6)

The symmetric difference is halved as a single element in the symmetric difference would involve breaking the tree without recombing and creating two distinct parts, which is not a valid transformation in our considered solution space. The distance d₁ is not itself calculated within the algorithms. Rather, it quantifies the degree of transformation that the heuristics perform. A transformation of distance 1 (or 1-neighbourhood transformation) occurs when an edge is removed, and the distinct parts of the tree are combined in a new manner. A transformation of distance 2 occurs when two such transformations are done simultaneously, providing a solution within the 2-neighbourhood of the initial solution.

Local search heuristics involve only 1-transformations in a single algorithm step. For capacitated tree problems such as pipeline networks, the metric described in Eq. 6 is typically implied when looking for solutions. A first-descent local heuristic uses the first discovered lower-cost solution as the new incumbent solution and repeats the process until no further single-step improvement is made, i.e. a local minimum is found. A steepest-descent local heuristic scans the entirety of its available 1-neighbourhood, then chooses the lowest-cost solution and restarts the process until no further single-step improvement is made. The term “local heuristics” will here onwards refer to any algorithm capable of exploring the 1-neighbourhood as described in this paragraph.

While a heuristic provides a way of making a transformation between two solutions, a metaheuristic considers more general strategies for reaching optimal solutions within the broader optimization space. Such methods can involve carefully chosen jumps into other neighbourhoods by invoking memory and allowing exploratory moves towards higher-cost solutions. Other examples performing parallel searches from different starting points in the optimization space, then converging towards a single solution.

We now provide three examples of local heuristics that serve as basis for exploring metaheuristics later, also serving as baselines for comparison with our contributions. Python source code is given for each algorithm in the provided Github repository.

2.3.1 Local Heuristics

Delta Change

The Delta Change (DC) algorithm was first introduced by Rothfarb et al. (1970) focusing on the optimal design of offshore gas pipelines. We give an elementary example of the cycle-based heuristic used by DC in Fig. 2.

Fig. 2

Core functionality of the Delta-Change cycle heuristic

An initial network solution is given in Fig. 2a. Two disconnected nodes are selected and joined to create a cycle within the network, shown in Fig. 2b. Note that the network in Fig. 2b shows constant pipeline thickness as capacity cannot be attributed due to the cycle. The cycle can be broken in three other locations, creating new potential candidates, shown in Fig. 2c. For each candidate, capacity is attributed and cost is calculated. As soon as a better solution is found, including within the iterations over a given cycle, the algorithm is restarted, categorizing the procedure as a first-descent heuristic. Until a better solution is found, the algorithm is restarted over new pairs of disconnected nodes. A similar algorithm is described by André et al. (2013) although the authors include a randomization of the list of nodes to initiate a cycle from, and limit the number of explored node pairs by only selecting the closest ones to the initial node choice.

Local Search

The DC cycle-based heuristic is also used in an algorithm described by Brimberg et al. (2003) referred to as “Local Search” (LS). However, in Local Search, a steepest-descent form is implemented, in which all the possible cycles of the 1-neighbourhood (all candidates over all potential cycles) are explored before the minimum-cost solution is chosen, provided that an improvement is found. More candidates are therefore evaluated, and the Local Search algorithm is expected overall to be slower than the Delta Change algorithm.

Edge Turn

Recently, another 1-neighbourhood search heuristic was proposed by Heijnen et al. (2020) within an algorithm we label the Edge Turn (ET) algorithm. The authors describe edge turns as an elementary heuristic to propose new candidate solutions. We provide an example of this elementary process in Fig. 3.

Fig. 3

Core functionality of the Edge-Turn heuristic

From a starting solution shown in Fig. 3a, an edge is chosen and is removed. As the starting network is a tree, two distinct connected components are created after the edge is removed (Fig. 3b). They can then be reconnected via a new edge that must (according to the edge turn process) necessarily include one of the two nodes from the removed edge. Such edges are shown in Fig. 3c. Candidate networks are then created as capacity is allocated and cost is calculated (Fig. 3d).

As the breaking and recombining is done in the same algorithmic step, the elementary edge-turn process can be compared to the one used in DC as each edge turn can be retrieved through an associated corresponding cycle. However, within ET, the number of allowed transformations is reduced as the recombination of the two parts of the tree must necessarily be done at one of the nodes of the removed edge. Heijnen et al. scan over all possible edge turns before choosing the lowest-cost solution if any is found, in a steepest-descent fashion.

2.3.2 Extensions into 2-Neighbourhood - Nested Heuristics

Extensions of the above heuristics can be conceived to permit jumps into the 2-neighbourhood of a graph solution in a single algorithmic step. This can allow discovery of lower-cost solutions, inaccessible via a 1-neighbourhood local search due to existence of local minima. Put simply, such algorithms enable discovery of better solutions that involve breaking and recombining the trees twice simultaneously, rather than twice in succession, as the first iteration may not lead to a lower-cost solution and the second iteration would hence not be explored. These algorithms can be described as nested versions of the 1-neighbourhood heuristics. The computational complexity of such algorithms increases vastly as another local heuristic (i.e. into the 2-neighbourhood) is performed for each tentative initial local heuristic (i.e. into the 1-neighbourhood). We shall include 2-neighbourhood extensions of the Delta Change and Edge Turn algorithms named Nested Delta Change (NDC) and Nested Edge Turn (NET). A nested version of the Local Search algorithm was attempted but rapidly disregarded as the long computational times were considered impractical. In the case of the Nested Delta Change algorithm, the first-descent characteristic from the 1-neighbourhood counterpart Delta Change (DC) is maintained in the 2-neighbourhood, such that as soon as a better solution is found, either in the initial 1-neighbourhood move or any of the associated 2-neighbourhood moves, the algorithm is stopped and restarted at this incumbent solution. For the Nested Edge Turn algorithm, the steepest-descent characteristic from the 1-neighbourhood counterpart Edge Turn (ET) is maintained over the full 2-neighbourhood, such that all 2-neighbourhood solutions are tried, and only the best new solution (if any) is chosen as the incumbent.

2.3.3 Metaheuristics

Metaheuristics are more general search strategies that orient the lower-level heuristics in the context of the larger optimization space, mainly by providing mechanisms to overcome local minima, and uncover global minima. The algorithms shown in Section 2.3.1 propose different ways of modifying networks one edge at a time. Local minima can be reached where no such further modification leads to a lower-cost solution. The algorithms in this section, allow modifications of networks by modifying multiple edges in a single step (such VNS or VS) or explore solutions that are not immediately lower cost but can lead out of a local minimum (Tabu Search). We give 2 literature examples of metaheuristics, Variable Neighbourhood Search and Tabu Search, and finally provide an original contribution algorithm, the High Valency Shuffle.

Tabu Search

Tabu search is a general method proposed by Glover (1989) and adapted to an oil pipeline design problem by Brimberg et al. (2003). When a local heuristic is not able to find a lower-cost solution, Tabu search proposes to explore solutions that add the least amount of cost to the local minimum. The lowest-cost solution is still stored and ultimately chosen if no better solution is found, but exploration to other higher-cost zones is permitted. Tabu Search makes use of a Tabu list of forbidden transformations. Therefore, in the case of a local minimum, the 1-transformation that increases the cost the least is chosen as the solution from which the next local heuristic shall be initiated. This transformation (or exchange of graph edges) is then added to the Tabu list, and the reverse transformation is prohibited by the algorithm. This last step avoids being potentially stuck in a loop between two solutions. The local heuristic used is the Local Search (Section 2.3.1), as per Brimberg’s implementation. The process is then repeated until a user-defined stopping criterion is reached, and the overall minimum-cost solution is returned. The stopping criterion used here is chosen as 10 times the duration of the previously defined Local Search, and the Tabu list has a maximal length of 7, identical choices to Brimberg et al. (2003). An illustration of the procedure is shown in Fig. 4.

Fig. 4

Basic method of the Tabu metaheuristic

From the local minimum, Tabu search explores the solution in the 1-neighbourhood that adds the least cost. A local search initiated from this new solution then obtains an global lower-cost option in the 2-neighbourhood of the local minimum. Note that neighbourhoods displayed are relative to the local minimum solution, and local searches starting from other solutions may cross over these barriers (as shown).

Variable Neighbourhood Search

Variable Neighbourhood Search (VNS) was initially proposed by Mladenovic and Hansen (1997) and was used by Brimberg et al. (2003). In the simple form proposed by Brimberg el al. implemented in this work, random jumps into new neighbourhoods are performed from a local minimum, successively reaching solutions at increasing distance (otherwise known as radius) from the local minimum, until a better solution is found. It therefore explores solutions that can have increased cost versus the current best solution, before attempting a local search in those new locations. Note that distance is defined by the specific metric used. Here, it relates to the symmetric difference of sets of edges and is given by Eq. 6. VNS therefore randomly breaks and recombines the local minimum tree as many times as required by the given search radius. The search radius progressively increases. At a limiting radius of 5 (as per the implementation of Brimberg et al.), if no better solution is found, the algorithm restarts at lower radius jumps again. The algorithm stops when a user-defined criterion is reached. The stopping criterion used here is 10 times the duration of a Local Search, as used by the Brimberg et al.. An illustration of the procedure is shown in Fig. 5.

Fig. 5

Basic method of the VNS metaheuristic

From the local minimum, VNS chooses to explore a solution in the 3-neighbourhood obtained from a random jump of radius 3. A local search then obtains an overall lower-cost solution in the 2-neighbourhood of the local minimum. Note that local search is not tied to moving “back” towards the local minimum and can move further from it.

High Valency Shuffle

The High Valency Shuffle (VS) is an original idea stemming from the repeated observation that many local minima solutions share the characteristic of having at least one high-valency node (>2 edges) that is distinct to a high-valency node found in the optimal solution. It is not based on a theoretical result but rather developed from repeated inspection of failures of other algorithms during this study. For a given high-valency node in a local minimum solution, a node situated in proximity to it may play a similar role in distributing flow but for a lower cost. The former solution represents a local minimum, and metaheuristics and heuristics alike can often be trapped within it. Indeed, none of the local transformations can transfer all the edges in a single step to another node, and incremental transfers over multiple steps do not necessarily provide lower-cost solutions. Within the data later shown here obtained from literature algorithms, we repeatedly observed that, only a full single-step switch of high-valency nodes can reach a lower cost solution. We provide a minimal working example of a network in such a local minimum in Fig. 6.

Fig. 6

Minimal working example of local minimum opportune for High Valency Shuffle

In Fig. 6a, the distances between nodes and node capacities are shown. The bolded numbers elsewhere in the figure correspond to individual pipeline cost values, with the network costs given by equations. Figure 6b displays the network T1 in a local minimum. A lower-cost network T2 is available in Fig. 6c but unattainable via local heuristics as steps to reach it require passing through higher-cost networks T3 or T4 seen in Fig. 6d and Fig. 6e, respectively. The network T2 can only obtained from T1 via a switch of multiple edges in a single step. Note that not all combinations of node capacity and node positions lead to a similar situation. The exact mathematical conditions leading to this general configuration were not studied in detail. While this transformation may be accessible via Variable Neighbourhood Search or Tabu search as they explore the wider optimization space outside of the local minima, they are sometimes too general to achieve such a useful node switch in a reasonable number of steps. Figure 7 gives a diagram of the High Valency Shuffle process.

Fig. 7

Core process of the High Valency Shuffle metaheuristic

This process appears similar to the one described in Fig. 5. However, the move to the solution in the 3-neighbourhood is not based on a specific amount of edge exchanges, but rather transferring all the edges from one node to another. Here the 3 edges from the central high-valency node in the local minimum solution have been transferred to the sink in the 3-neighbourhood solution. A High Valency Shuffle move can therefore correspond to an arbitrary neighbourhood change within the metric described in Eq. 6.

This metaheuristic is in fact an interplay between two distinct metrics when used with the lower-level heuristics shown here. The first is the previously mentioned d₁ metric based on the symmetric difference between sets of edges. This metric is used by the lower-level heuristic that breaks single edges and reassembles trees once at each step. The higher-level metaheuristic transfers multiple edges in one step. It can be nonetheless described as making transformations within a distinct metric space, described by the symmetric difference between the sets of nodes with more than 2 edges. As such, transferring edges from one high-valency node to a low-valency neighbouring node (irrespective of the number of edges), is a 2-transformation within the high valency node metric space. Distance d₂ between two solution networks T1 and T2 in this metric space is defined by (Eq. 7):

$$ {d}_2\left(T1,T2\right)=\left| HV(T1)\triangle HV(T2)\right| $$

(7)

Where HV(T1) refers to the set of nodes with more than 2 edges in the network T1. The High Valency Shuffle metaheuristic is used in combination with a lower-level local heuristic. We describe the algorithm by pseudocode in Table 1. Local transformations within the d₁ metric space are initially performed until a local minima is found (Step 0) and an empty solution list is initiated (Step 1), at which point high-valency nodes are identified (Step 2) and transformations within the d₂ metric space are attempted space in search of better solutions (Step 3). At every tentative transformation in d₂ space of Step 3, a local search in d₁ is performed (Step 3c). The algorithm restarts at step 3 if a better solution is found.

Table 1 High Valency Shuffle Metaheuristic

In this study, we use three lower-level local heuristics (seen in Step 3c) in combination with the High Valency Shuffle. Edge Turn (VSET), Delta Change (VSDC), and Local Search (VSLS), all described previously, are therefore used simultaneously with the metaheuristic. Combining the proposed metaheuristic with other metaheuristics (Tabu, or VNS) was deemed too computationally demanding. For example, an individual Tabu Search already requires ten times the duration of a Local Search. Furthermore, the metaheuristic is evaluated on its ability to guide local heuristics. Tabu and VNS themselves already represent lower-level heuristic guides and it would become unclear which metaheuristic is responsible for overcoming local minima. The High Valency Shuffle is described by pseudocode in Table 1.

3 Results

3.1 Generated Networks

To evaluate the proposed heuristics and metaheuristics and compare with literature options, we initially perform tests on generated data, with randomly placed source and sink locations as well as source capacities to gauge the algorithms' effectiveness on a variety of input data. We use the aforementioned heuristics and metaheuristics on an increasing number of sources and compare calculation times to the fraction of optimal networks found. All calculations in this paper were performed in similar conditions on an Intel i7-8565U CPU. For the smaller network comparisons, optimal networks were discovered through a brute force method, obtained by comparing all the possible trees, obtained from Prüfer sequences (Prüfer 1918). For larger network comparisons, due to impractical computational times for the brute force method, the best-found tree for all the algorithms was used for the optimal comparison. In each random graph the sources and sink were placed randomly on a square following a uniform distribution law. Source capacities C were attributed according to the following law: C = X³ where X is a random uniformly distributed variable scaled between 0 and 100. The use of a power-type law imitates the distribution of CO₂ source capacities, heavily skewed towards smaller values, observed in the ETS data. A comparison between a generated distribution from this law and the ETS node capacities is shown in Fig. 8.

Fig. 8

Comparison of node capacity distribution between ETS data and data generated from the power law

As an exact fit to the ETS emission volume distribution was not the desired outcome, the rapidly decreasing power law fit was deemed a reasonable approximation for industrial CO₂ emission distribution volumes, but nonetheless allows enough difference with the real-world capacity distribution for comparative argumentation. The ETS data notably shows a large concentration of small values and a thinner tail. As the cost function in this paper (Eq. 2) does not include added constants, the scaling of X is does not affect the calculation results. The scaling of X between 0 and 100 was done to avoid extremely small differences in cost between solutions that are of the order of floating-point value errors. The sink capacity was set as the opposite of the sum of the source capacities to ensure material balance. The Minimum Spanning Tree was used as a starting point for each algorithm, as shown in Fig. 1.

Figure 9 displays the generated graph results for smaller networks with a direct comparison to a brute force method result.

Fig. 9

Algorithm performance comparison for small networks with a direct comparison to guaranteed optimal network

We make a few observations regarding the performance of the various algorithms on the small networks shown in Fig. 9. There exists a general trade-off trend between calculation time and optimality in which increased calculation time leads to increased rates of optimal solutions. All the new algorithms proposed here (Nested Edge Turn and Nested Delta Change, and all High Valency Shuffle Algorithms) lead to better optimality at the expense of longer calculation times. The High Valency Shuffle Algorithms obtain a 100% optimality rate in most of the cases while being faster than the Nested Algorithms. As the number of sources increases, calculation time for all algorithms increases, and the optimality of all algorithms seems to decrease but remains high for the High Valency Shuffle Algorithms, notably for the larger graph sizes of 7 and 8 sources.

Figure 10 displays the generated graph results for larger networks without a direct comparison to a brute force method result.

Fig. 10

Algorithm performance comparison for larger networks. The asterisk refers to the fact that the optimal network comparisons are not guaranteed to be globally minimal

As the number of sources increase, we continue to observe a loss of optimality for all algorithms, except only the High Valency Shuffle algorithms, which demonstrate optimality rates upwards of 95% in all cases. The Nested Algorithms, despite their large calculation times, fail to capture the best network solutions in the larger networks. These will therefore be excluded in some of the case study examples as they are impractical.

We note that the first-descent algorithms (DC, NDC), perform worse than other steepest-descent algorithms (for example LS, ET and NET) specifically for smaller graphs (5–9 sources). Indeed, they lie below the general trend of trade-off between calculation time and optimality for the 6,7 and 8 sources case. We propose the following explanation. We suspect this is partly explained by the highly skewed distribution of node capacity which may encourage the creation of local minima around high valency nodes. For a first-descent heuristic, finding an optimal solution requires the possibility of “undoing” a move that was locally advantageous but not leading to an optimal solution. The existence of the high valency nodes that create local minima described in Section 2.3.3 is contrary to this. The weak performance of first-descent heuristics for the specifically small graph sizes also points in this direction. For small networks, there is usually only one or two very high flow-carrying pipelines. With first-descent heuristics, these may initially be set up in configurations that are suboptimal, and further improvements to the networks around this initial choice may simply cement them as local minima around high valency high flow-carrying nodes. As these pipelines contribute the most to cost, they are set correctly faster by the steepest-descent algorithms. At larger graph sizes, more local optimization steps are required reach the solution from the initial MST. The setup advantage of steepest-descent strategies is lessened as the diversity of optimization paths available gives ample possibilities to create local minima. We hypothesize therefore that at larger graph sizes, the relative performance of the first-descent algorithms does not increase, but rather the performance of the steepest-descent algorithms decreases to the level of the first-descent algorithms.

3.2 Case Study: Grid Search Procedure over CO₂ Sources

As a case study of the algorithms, rather than using generated data, we use regional clusters of German industry CO₂ source locations and emission quantities as initial input data. As well as using these sources, we create a grid of potential sink points surrounding the clusters and iterate the network optimization algorithms over each potential sink location. We both test the speed and efficiency of the algorithms in finding the optimal graph solution and get an indication as to where the optimal sink location is placed. Large-scale CO₂ networks are not yet in place in Germany, despite its status as the largest CO₂ emitter in Europe. We propose idealized but reference solutions for overall pipeline layouts of regional clusters, providing an idea of the location of an optimally placed sink node. In practical terms, a sink could mean an underground storage facility, the final link of a Carbon Capture and Storage chain. CO₂ storage may not be technically possible or politically desired in the optimal locations. Nonetheless, these sink locations can alternatively be seen as a collection point for a larger, multi-level CO₂ network, with a final cross-border output and final underground storage location in the North Sea (European Commission 2021). This vision is encouraged by the recent public consultation of the European Commission regarding legal cross border CO₂ transport and storage, and pilot storage projects in the North Sea (Hannis et al. 2017).

All other aspects of the generated networks Section 3.1 are maintained. Total network cost is only given by pipeline cost (Eq. 3). However, in a comprehensive cost analysis, individual CO₂ source collection costs, and CO2 storage costs depending on the sink location would need to be considered.

We present the CO₂ source clusters used as input data for the sink grid search. The CO₂ source clusters considered are shown by different colours in Fig. 11. They are numbered from 1 to 5 in order of increasing number of points. Source clustering was done using a DBSCAN (Ester et al. 1996) algorithm. We limit ourselves to only a few emission clusters to demonstrate the algorithm effectiveness. The sources in grey without a cluster number are therefore not considered here initially.

Fig. 11

Left: CO₂ source clusters considered in this work. Right: lowest-cost networks obtained for each cluster, with optimal sink location shown as a red cross

Emission quantities were taken as a 3-year average of years 2015–2017 for emitters listed in the EU Emissions Trading Scheme (ETS) database and georeferenced to provide coordinates. Some further alterations to the dataset were made. Emissions whose primary activity was energy production were removed, as these sources (mainly coal plants) have an uncertain future in the German emission landscape, with the planned phasing out of large coal-fired plants before 2038 at the latest (German Federal Ministry for Economic Affairs and Energy 2020). Through this omission, 73% of the total emission quantity is not considered. The created networks would be significantly different with the inclusion of energy sources. However, the omission renders the proposed CO₂ emission landscape coherent with ongoing decarbonisation efforts in Germany. As the energy source removal was done on a basis unrelated to position or capacity, this removal process is believed to not influence the overall efficacy of algorithms studied here for CO₂ emission network scenarios. Finally, individual sources emitting annually less than 50,000 tons of CO₂ per year were excluded to reduce the number of points in the potential networks. Low emission volumes are also not expected to be included in pipeline infrastructure due to the increased relative costs (Elegancy 2020). These small sources (not shown here) represent a further reduction of 3% in total emission quantity. In some cases, different emission sources occur in the same location, and are listed as different contributors. For the network optimization procedure, sources with the same coordinates are combined as a single node with emissions summed together. From Fig. 9, we see that the distribution of node capacity is notably more rapidly decreasing and thin tailed than for the generated node capacity distribution studied in Section 3.1. The spatial distribution of nodes within a given cluster, is observed to be slightly elliptic in shape. However, we consider that within a given cluster, the spatial distribution appears relatively uniform, especially bearing in mind that nodes with the same coordinates are combined.

Details of the individual cluster can be found in Table 2.

Table 2 Details of CO₂ source clusters

The potential sink locations were chosen within a grid given by the convex hull +50 km around each source cluster. The number of sink locations was adapted each time to the network complexity to account for large calculation times. The algorithms and number of sink points tried for each cluster are given in Table 3. The algorithms considered are Edge Turn (ET), Delta Change (DC), Local Search (LS), Nested Edge Turn (NET), Nested Delta Change (NDC), Tabu Search, Variable Neighbourhood Search (VNS), High Valency Shuffle with Edge Turn (VSET), High Valency Shuffle with Delta Change (VSDC), High Valency Shuffle with Local Search (VSLS). For the three largest clusters, some of the algorithms required extremely large calculation times. For the clusters 3, 4 and 5 the nested algorithms were therefore omitted, also owing to their lower performance demonstrated in the previous section.

Table 3 Numerical details for the grid search around the source clusters

Finally, a comparison to a known optimal solution was only possible for the smallest cluster. Iterating over all possible trees rapidly becomes too computationally impractical for other clusters. For the other clusters, the optimal tree considered was simply taken as the minimum-cost tree for all the algorithms but is not guaranteed to be globally minimal.

Grid search results are summarized in Fig. 12 with colours consistent with clusters shown in Fig. 11.

Fig. 12

Grid search results comparison. Only for Cluster 1 is the comparison to a guaranteed global minimum possible

Through these grid searches we see that the conclusions obtained with the generated graphs are generally maintained, notably the graphs solutions obtained from the Valency Shuffle algorithms are often optimal, except when used in combination with the first-descent local heuristic DC. Their performance is particularly superior for the largest clusters, such as cluster 5, and well-above all other literature algorithms considered with similar calculation times such as Tabu and VNS.

We note that the poor performance of the first-descent strategies is even more marked than previously observed in Section 3.1. This is coherent with the increased skewedness of the ETS data node capacity distribution (Fig. 9) and fits with the tentative explanation given in Section 3.1. Once again, first-descent algorithms alone show worse performance, particularly for small graphs. This relationship between first-descent heuristics and node capacity distribution is unexplored in the literature, and good performance of the first-descent heuristic Delta Change is shown for uniform node capacity distributions only. Heijnen et al. (2020) use a uniform distribution for source capacity and find that the Edge Turn algorithm performs roughly equivalently to the Delta Change algorithm for networks without Steiner nodes. André et al. (2013) also evaluate the performance of the Delta Change algorithm in comparison to Tabu Search for networks with 6 nodes with constant node capacity. The authors find that the first-descent algorithm performs at least as well as Tabu Search for most cases.

One comment concerns the choice of lower-level heuristic to use in combination with the High Valency Shuffle. As described previously, the steepest-descent algorithms (LC and ET) seem to perform better in combination the VS metaheuristic. It also seems that a fast but mid-fidelity steepest-descent heuristic (such as the Edge Turn algorithm) achieves almost equivalent optimality rates when combined with the High Valency Shuffle metaheuristic (VSET) as better performing, but slower, lower-level heuristics such as Local Search (combined as VSLS). In other words, differences in performance of the (steepest-descent)lower-level heuristics do not seem significantly affect the result obtained when used in combination with the High Valency Shuffle metaheuristic. In this regard, it becomes useful to employ a fast lower-level heuristic (such as the Edge Turn algorithm) in combination with the High Valency Shuffle for the best combination of optimality and speed. This leads us to speculate that an even faster lower-level heuristic exploring a reduced fraction of the 1-neighborhood might be sufficient to provide similarly high optimality rates in combination with the High Valency Shuffle and further decrease the overall calculation time. We explore this further in the discussion Section 4.3.

In the Appendix we display the detailed results of the grid searches for all sink locations, presented on top of the original sources, with some discussion. The results are compared through maps showing the location of non-optimal solutions and deviation from optimal cost.

4 Discussion

4.1 High Valency Metric – Another Route for Improvement

As described in the Materials and Methods section, the High Valency Shuffle metaheuristic escapes local minima by switching the edges of high-valency nodes to their closest neighbours and eliminates (if any) created cycles before applying a local heuristic and then choosing the lowest-cost solution. A typical transformation allowed by the High Valency Shuffle metaheuristic with Local Search is shown in Fig. 13a. In this example, taken from the grid search of cluster 2, the potential sink is represented by a black circle and the sources are shown in magenta. The sink location remains the same within both panels. The network to the left of Fig. 13a is the result obtained from the Local Search. The network to the right of Fig. 13a is the result obtained from the High Valency Shuffle with Local Search, which is found to have a cost 5% lower. The edges of a high-valency node highlighted by a dashed circle are transferred to a different node, as expected. To obtain the lower-cost graph from the first, the number of 1-transformations in the symmetric difference of edges metric is three. Within the proposed high-valency metric, this is equivalent to a 2-transformation. Indeed, the set of nodes possessing more than two edges has changed by two elements.

Fig. 13

Final graphs obtained using different algorithms. In both cases the transformation to the lower cost graph involves a local 1-transformation in the proposed high valency metric space

However, in Fig. 13b, the graph to the left is a suboptimal result obtained from the High Valency Shuffle with Local Search. The graph on the right is a lower cost solution found with the Nested Delta Change algorithm. The lower-cost solution possesses an extra high-valency node. We can see that the High Valency Shuffle was unable to add an extra element in the set of high-valency nodes. Instead, it relies on switching edges of high-valency nodes to other nodes. The transformation seen in Fig. 13b is nonetheless a 1-transformation in the high-valency metric space described by Eq. 7 but is not captured by the High Valency Shuffle metaheuristic. Most suboptimal solutions provided by the High Valency Shuffle metaheuristic are observed, upon inspection, to require this type of transformation.

The inclusion of a heuristic that could construct high-valency nodes without transfer from a prior high-valency node would be beneficial for achieving higher optimality rates.

4.2 Algorithm Performance Analysis and Application to Large Graphs

The calculation times from randomly generated graphs in the previous section are displayed in Fig. 14 as a function of the number of sources in the network. The straight lines seen in the log-log plot are indicative of exponential time algorithms. The curves are therefore fitted to a power function of the form: t(n) = An^B, where t(n) is the calculation time in seconds, given in terms of the number of sources n. A and B are the variables to fit. To achieve this, the curves are fitted by minimum least-squares to a linear function in log-log space, with a weight function given by $w=\sqrt{t}$. The weighting is included to avoid the intrinsic bias of fitting a transformed function in log-space in which a disproportional weight is given to the points with smaller y-axis values. The results from the curve-fitting are shown in Table 4.

Fig. 14

Time complexity comparison of the algorithms described in this study

Table 4 Power law fit parameters for the time complexity analysis: The algorithms’ performance is fitted with the function t(n) = An^B with t in seconds

Finally, a test is done on a large graph composed of CO₂ sources not included in the clusters from the previous section. Within this CO₂ source cluster, there are 143 emitters at 94 distinct locations. Combining the sources from the same locations gives a network of 95 nodes, including the sink. Due to the large number of nodes in the cluster, only a single sink location was considered and placed at the centre of gravity of all the sources, weighted by emission quantity. All algorithms were tested but stopped if not completed before a reasonable period of time (48 h). The lowest-cost graph was only obtained using the High Valency metaheuristic in combination with the Edge Turn heuristic. Predicted calculation times, measured calculation times and obtained relative graph costs, when applicable, are shown in Table 5. The cost difference of the network created from the Minimum Spanning Tree (MST), which simply minimizes network length, is also given for comparison.

Table 5 Details of the network design modelling of the large final CO₂ source cluster

To better visualise the results from this final example, the spatial networks are shown in Fig. 15. The compared algorithms are Local Search (LS), Variable Neighbourhood Search (VNS), Delta Change (DC), Edge Turn (ET), Tabu Search (Tabu) and High Valency Shuffle with Edge Turn (VSET). A comparison with the solution obtained from the Minimum Spanning Tree (MST) is also given. The lowest-cost network obtained with the VSET metaheuristic is shown with pipelines in grey. Network differences with the lowest-cost network for other solutions are shown in red, whereas sections of the networks shared with the lowest-cost solution are also left in grey. For clarity, the sources are displayed with a small, constant size, despite contributing differently to the network flow. However, the line thickness remains representative of flow quantity. The sink node is shown as a black square.

Fig. 15

Final comparison on algorithms with reasonable (<48 h) calculation times on a graph with 95 nodes

Extensions of the current study could typically include investigations of the optimality and time complexity of the proposed VS algorithms for different capacity exponents in the cost function shown in Eq. 2. At higher capacity exponent values, such high-valency nodes appear rarer as the optimal network approaches hub networks. At lower capacity exponent values however, high valency nodes will indeed exist, and the VS algorithms should retain their effectiveness.

4.3 Further Algorithm Tweaks

From the concluding remarks in Section 3.2 regarding the high performance of mid-fidelity, fast, steepest-descent local heuristics with the VS metaheuristic, we attempt to further decrease calculation time of the VSET without losing performance. For this, we limit the exploration nodes accessible during a potential edge turn. Therefore, when an edge is removed, it can only be reconnected to a limited number of closest nodes belonging the other connected components. This will reduce the search space in comparison to the generic version of ET in which all the other nodes of the opposite connected component are explored. We name the new versions of ET: “Reduced Edge Turn”, and always accompany the algorithm with the maximal number of nodes allowed for exploration, named n_e. A Reduced Edge Turn heuristic that is only allowed to explore up to 5 nodes on either connected component, would then be named RET-5. Similarly, VS algorithms combined with these algorithms also carry the number of closest nodes explored, leading to notations such as VSRET-5. We compare the results against the largest randomly generated graphs (28 sources) from Section 3.1, where the VSET algorithms performed very well. The results are visible in Fig. 16. We show results for the RET algorithms alongside the VRET algorithms. As expected, we observe a reduction in calculation time for the reduced versions of both the ET heuristics (RET-n_e) and the reduced VS metaheuristics (shown by the VSRET-n_e markers). The reduced solution space exploration has little effect on the performance when n_e remains high. We observe a performance decrease for the smaller values of n_e, with the first decrease at n_e = 9, roughly a third of number of sources in the graph. For n_e = 12, performance was maintained but calculation time was halved. Finally, it seems that the reduced performance of the metaheuristic is in fact tied to the reduced performance of the RET algorithms as they also first show reduced performance at a n_e = 9.

Fig. 16

Reducing calculation time by limiting the number of exploration nodes in the VSET algorithm

We conclude that reducing the number of exploration nodes for the ET algorithm in the VSET metaheuristic represents an easy way to decrease calculation time while maintaining full performance. Furthermore, we expect that using around a third of the graph size as exploration node number n_e seems to be a safe estimate to ensure performance.

5 Conclusion

In this paper we have conducted performance comparisons on graph optimization heuristics and metaheuristics aimed at achieving Minimum-cost Capacitated Spanning Trees within the context of pipeline network design. In the search for lower-cost solutions, we attempt nested solutions of literature algorithms that enable unoriented explorations into wider optimization spaces in a single algorithmic step. These solutions provided higher rates of optimal networks than literature options, at the expense of larger calculation times. A new metaheuristic and associated distance metric, providing a relevant quantification of difference between solutions, were developed that captured useful network transformations easily. Such transformations had required a large amount of algorithm steps previously and were often not accessed at all. The High Valency Shuffle, switching the edges of nodes with more than two edges to neighbours, proved to achieve almost 100% optimal networks in most examples used. The calculation times for the new metaheuristic, while large, remain comparable to current literature options such as Tabu or Variable Neighbourhood Search while achieving greater proportions of optimal solutions. The new metaheuristic is used in combination with a local heuristic, the choice of which seems to influence little the resulting solution cost but has a large effect on calculation time. It seems therefore beneficial to combine the High Valency Shuffle with a fast, steepest-descent, local heuristic which may by itself only achieve low rates of optimal solutions.

6 Appendix

1.1 Grid search results

The grid search results are displayed on top of the original sources, showing for each potential sink location, a small square if the solution found is not optimal. Furthermore, the cost difference from the optimal solution is displayed as a colour gradient within the square. The cost of the minimum-cost network found (either guaranteed optimal for cluster 1 or minimum overall solution for the other clusters) is shown on a separate map and named “optimal cost”. The lowest-cost sink of all potential sink locations is indicated by a red cross. The map of isomorphic graph zones for the overall lowest cost solutions is shown for some clusters. Isomorphic graph zones display areas in which the graphs share the same list of edges, i.e. are structurally the same but may have varying edge lengths or costs. They are illustrative of the variety of optimal solutions occurring over a large space of potential sink locations. Also, the isomorphic graph zones can represent a weak proof of global optimality of solutions. Indeed, continuous zone boundaries and a lack of “island” solutions (i.e. a single location or small number of solutions fully surrounded by a different, single isomorphic graph zone) are to be expected with globally optimal isomorphic graph zones. For the clusters with a lower number of sink locations (i.e. clusters 4 and 5), we do not display the optimal isomorphic zones. The low spatial density of sink locations leads to each sink location usually belonging to its own individual zone and the map does not convey any information. For each sink location, we do not display the obtained graphs as the optimal topology is of little importance with regard to the algorithm’s effectiveness. This would be also impractical due to the large number of sink locations. For completeness, we give the minimum-cost tree for the lowest-cost sink location in each of the 5 CO₂ source clusters considered in Fig. 11. Some algorithm results are not displayed in the following maps Figs. 17, 18, 19, 20, 21 as they achieve optimal solutions at every sink location. Finally, in cluster 1, the results obtained for certain algorithms were the same and are shown in a single map.

Fig. 17

Cluster 1 grid search results. Local Search, Edge Turn and Delta Change here only show one non-optimal solution adjacent to the top rightmost source

Fig. 18

Cluster 2 grid search results

Fig. 19

Cluster 3 grid search results

Fig. 20

Cluster 4 grid search results

Fig. 21

Cluster 5 grid search results

Some new information can be gathered from the grid search results in map form. First, only sink locations on certain optimal isomorphic zones tend to lead to failure of the various algorithms. For example, suboptimal solutions from the DC algorithm in Fig. 18 are concentrated as a group in the lower part of the source cluster, with a distinct boundary appearing around the centre of cluster, after which a transition to optimal solutions occurs. This could indicate that there exists a common step in the DC algorithm for these sink locations that leads to a local minimum. Furthermore, we can observe common zones in which suboptimal solutions were fond with all the local heuristics (LS, ET, DC), and only with the use of a metaheuristic was the optimal solution found. One example is the long vertical streak of suboptimal solutions in the lower part of the map in Fig. 19 common to LS, ET and DC.

Next, we can note that the local heuristics ET and DC, share many of the same suboptimal sink locations as either their nested versions (NET, NDC) or the versions included within the Valency Shuffle metaheuristic (VSET, VSDC). This is seen for example in Fig. 19, where the squares corresponding to suboptimal sink locations for the VS metaheuristics are all included with the maps of suboptimal sink locations of their corresponding lower-level local heuristics. On these squares, the Valency Shuffle metaheuristic did not achieve a better solution. The large number of suboptimal solutions for the VS metaheuristics was examined in detail. Upon inspection of the suboptimal solutions proposed, we found that all correspond to local minima similar to the one illustrated in Fig. 13b. In these cases, a 1-transformation in the high-valency node metric space is required, but the proposed metaheuristic is incapable of achieving it as previously discussed in Section 4.1.

Finally, we can comment on the maps showing the network cost for each sink location. The cost of optimal networks can increase up to almost 180% depending on the location of the sink. The sink location is therefore a crucial parameter in network design. Where there is a sufficient level of sink location density, we can distinguish a two different categories of optimal sink location. The lowest-cost sink location is sometimes situated on large sources (Fig. 18), but otherwise in between sources (Fig. 17, Fig. 19). These locations correspond to in fact to weighted geometric medians of the sink neighbours weighted by capacity transferred to the sink. A heuristic algorithm designed to locate the lowest-cost sink location in network without defined layout is proposed by Yeates et al. (2021) and is currently the subject of ongoing research.