The Core of the Global Corporate Network

Abstract

We investigate the network topology of a comprehensive data set of the world-wide population of corporate entities. In particular, we have extracted information on the boards of all companies listed in Bloomberg’s archive of company profiles in October, 2015, a total of almost 100,000 firms. We provide information on board membership overlaps at various levels, and, in particular, show that there exists a core of directors who accumulate a large number of seats and are highly connected among themselves both at the level of national networks and at the worldwide aggregated level.

1 Introduction

The structure and formation of corporate networks has intrigued researchers from diverse scientific fields and the public in general for a long time. Corporate governance structures can be cast into the format of a network due to the fact that often members of a corporate board are serving on the boards of two or more companies, thus generating a network of connections between different companies. This network has been characterized as belonging to the class of small world networks (see, for instance, Battiston and Catanzaro 2004, or Sankowska and Siudak 2016). Consequently, only a few degrees of personal connections are necessary to transverse the whole network.¹ Some questions naturally arise: Are the network structures the result of purposeful creation of links by some influential elite? Or are they just unintended outcomes from multiple individual and isolated choices? Regardless of the academic discussion, there is also a growing public concern that a relatively small group of people have close personal inter-connections while managing/controlling together a large share of the world economy.

The basic empirical question posed by these different viewpoints is whether there is something unexpected in the network structure of board interlocks, i.e. structural features that could not be explained by a simple null model of appointments of board members and that would require the development of more involved sociological and/or economic models of how firms choose their board members with an eye on their connections to other boards.

The present paper contributes to the recently burgeoning literature on the structural features of corporate board interlocks. In particular, we revisit the network properties of corporate boards using a nearly comprehensive worldwide database, that also allows us to analyze interlocks across national borders besides domestic ones. Namely, we have gathered all board members listed in Bloomberg’s archive of company profiles. The number of companies for which board information is available, amounts to almost 100,000. This is more than twice the number of listed companies worldwide. Although it seems impossible to identify by what criteria their large data set has been constructed from the even larger universe of all corporate entities worldwide, it is likely that it covers completely all firms beyond a certain size in countries that are integrated in the world economy to a certain degree and that it might constitute a more incomplete sample of the lower end of the size distribution of firms. However, we are mainly interested in those companies whose boards have overlaps with other firms and are not completely isolated. Their number in the database is almost 82,000 and since these will be the more visible ones it seems likely that the data base covers this interesting subsample to a very large extent, if not almost completely.

Following the approach of Milakoviç et al. (2010), we confirm their results of a highly significant deviation from a random null model both for many of the countries included in our data base and for the aggregate worldwide board network as a whole. We also investigate this issue from a slightly different angle by studying the so-called “rich club” phenomenon. The “rich club” statistics quantifies the tendency of the dominant members of a network (in terms of their degree) to form tightly connected communities. Again, we find strong indication of the presence of this phenomenon in the international board network. Taken together, our results, thus, indicate that not only is the accumulation of multiple memberships a non-random event, but also that directors with a high number of seats are unexpectedly highly connected (i.e. have more joint appointments than expected by random assignments, even taking into account the higher chances of overlaps for directors with multiple positions). Beside these key results the paper also provides some additional insights into the features of the worldwide board network in terms of the role of different countries and economic sectors.

The paper proceeds as follows: The following section offers an overview over related previous research on board interlocks from a network perspective. Section 3 provides information on the data set used and some descriptive statistics. Section 4 defines the network statistics used in our analysis, and Section 5 presents our empirical results on interlocks at the national and international level, and on the importance and degree of international integration of different countries and economic sectors in the worldwide board network. Section 6 discusses potential explanations of our findings and Section 7 concludes.

2 Related Literature

Research on the topology and economic relevance of interlocks between corporate boards has been burgeoning over the last few decades and has benefited greatly from methodological advances in the broader area of network science that has established itself since the 1990s. The long legacy of research in corporate networks is exemplified by the seminal volume by Mizruchi (1982) who studies the close connections between a relatively small sample of 167 firms in the USA from 1904 to 1974 documenting that this sample of the most important firms constitutes what would in modern terminology be denoted a large connected component.

The development of structural network models has spurred a large literature attempting to characterise board interlocks using the new formal approach to network analysis from the natural sciences. Evidence for small-world properties of this network has been reported by, among others, Davis et al. (2003), Conyon and Muldoon (2006) and Kogut (2012) for the U.S., Milakoviç et al. (2010), (2015) and Raddant et al. (2017) for Germany, Battiston and Catanzaro (2004), Bellenzier and Grassi (2014) and Clemente et al. (2018) for Italy, Raddant and Takahashi (2019) for Japan and Biswas (2020) for India. These contributions find that board networks resemble small world networks and exhibit positive assortativity. Often the authors argue that the concentration of a multitude of board seats in the hand of few individuals constitutes a significant deviation from a null model in which board positions would be independent random draws assigning a fixed population of directors to a given number of board positions.

Similar results are documented for networks of ownership by Kogut and Walker (2001) for German data and by Vitali et al. (2011) and Glattfelder and Battiston (2019), for a broad international data base. Several of the mentioned papers go beyond identifying structural characteristics and attempt to identify leading players within the network. Milakoviç et al. (2010), (2015) and Raddant et al. (2017) show that there is a significantly non-random hierarchical structure in the German board network with a closely knit ”core” that remains structurally stable over time. Milakoviç et al. (2015) also emphasize that this unlikely concentration of multiple positions within a single subset of the largest companies survives over time, irrespective of the change of personnel and even the entry and exit of firms to and from the corporate core of the economy. In a similar vein, Vitali et al. find a “bow-tie” structure of the international ownership network in which transnational corporations constitute the closely connected core.

The finding of significant clustering of interlocks now apperas to be a well-established empirical fact. Possible explanations of this phenomenon fall into various categories: (i) corporate social interlocks could be a result of favoritism and thus would reflect existing personal relationships in the elitistic circles of a society, (ii) joint board positions could be an effective way of learning about managerial practices or (iii) could be a reflection of material entanglement of interests between firms, such as a link with its corporate clients, or firms along a supply chain. Finally, (iv) board interlocks could just be the imprint of certain individuals with extraordinary capabilities as supervisors being in high demand so that they receive multiple offers to serve on corporate boards. Any of the more economically oriented explanations should, in principle, be testable by scrutinizing the hypothesis of a link between board overlaps and firm performance.

An increasing body of research has indeed embarked on investigating whether board interlocks are an imprint of ‘crony’ capitalism or whether they are a valuable source of acquisition of information or expertise to a firm. However, empirical evidence on this issue is mixed. Some studies did rather find a negative effect of busy directors on performance criteria. Such a finding would be in line with decreasing returns to supervision but would demand a non-economic explanation for why interlocks exist in the first place despite the inefficiency of overburdened holders of multiple seats. Andres and Lehmann (2010), for instance, regress various measures of firm performance on centrality statistics computed for the members of the supervisory boards of German DAX30 companies. They find that higher centrality is associated with lower performance but higher compensation of board members, a result that is in line with the sociological hypothesis of an organisational elite that is not chosen according to economic performance criteria.

The findings of Andres and Lehmann (2010) have been confirmed by Böhler et al. (2010) showing also that only foreign investors are sensitive to this negative effect of high connectivity while domestic investors in Germany appear rather to assign value to it. Results for other countries are somewhat more muted: Biswas (2020) finds that in the Indian corporate board network companies which via joint appointments act as a bridge between otherwise unconnected communities enjoy a positive effect of these interlocks on performance. Faia et al. (2020) present evidence that supports the economic view of value creation through communication. They analyse the effects of a change in corporate regulations on the value of Italian listed companies. In 2011, a law has come into effect prohibiting multiple board positions in insurance and finance companies. As Faia et al. show companies whose centrality in the network had been reduced by this regulation suffered from losses in the stock market. Hence, this provides evidence of the stock market assigning a positive value to higher centrality.

An even broader, closely connected literature studies the effects of connections between directors via social networks. For instance, Hwang and Kim (2009) find that the compensation of CEOs is higher if they are socially connected to some directors of the same company. Nguyen (2012) shows that accountability of CEOs is lower if they are socially connected with directors of the same firm. Souther (2018) finds that closer social proximity within a board is correlated to lower market valuation and higher director compensation. Since our analysis uses data on corporate boards only, we are unable to shed light on the relationship between board interlocks and economic performance. However, we will provide evidence that board interlocks across national borders show similar hierarchical tendencies like national ones.

3 Data Description

Data was collected from the Bloomberg website in October 2015. More specifically, board membership information both from public and private companies was collected from specific pages such as http://www.bloomberg.com/markets/api/management/board/DBK:GR for Deutsche Bank, as an example. Other company specific information (such as address and sector classifications) were collected from pages such as http://www.bloomberg.com/markets/api/quote-page/DBK:GR, again for Deutsche Bank as an example. Board members of all companies listed were extracted and links between boards via common members have been established. The complete list of companies is available in the http://www.bloomberg.com/robots.txt web file. For a similar approach of information retrieval through web crawling of a large data base see Fire and Puzis (2004).

Board membership information was represented by means of incidence matrices, which allow for the calculation of network measures. Two directors are said to be connected if they hold seats in the same company, and two companies are said to be connected if at least one common director serves on their boards. This network can be analyzed in its bipartite form, and it can be transformed into a unipartite network of overlaps considering either directors or companies as nodes. In both cases, the incidence matrix M is the same, and the respective adjacency matrices can be computed by the projections D = MM^T and C = M^TM.

A particular feature of the network of board affiliations D is the existence of node communities by construction (the boards), resulting in complete subgraphs in which all nodes (the board members) are connected to each other. This feature has an impact on some specific network properties: the existence of such communities produces trivially high average clustering coefficients, for example. In addition, the degree of a board member depends on the size of the boards in which she/he has a position. Hence, two members in equally connected but differently sized boards would have different degrees.

To alleviate this particular feature, we restricted attention to the more interesting cases of directors who serve in at least two boards. With this restriction, all the trivial links within the same board are removed, and only connections between directors are counted as links that extend beyond one single board. As a consequence, the degree of each director now counts his contacts to other directors who have at least two board positions, and is not inflated by the number of single-seat colleagues in the same board (which actually is to some extend an idiosyncratic number for different firms and not of major interest for our analysis). The subgraph formed by the network of board members holding at least b = 2 positions (referred to as D₂) keeps all important information with regard to overlaps in the entire network, but removes the influence of different board sizes. Thus, here only the network of members holding multiple (at least two) positions is considered. It is worthwhile to note that this definition of b-core (b for board positions) is different from that of k-core (k for degree). A k-core (or k-degenerate graph) is the (unique) maximal induced subgraph with nodes of a minimum degree of at least k. Alternatively, the k-core is the (unique) result of iteratively deleting nodes that have degree less than k, in any order.

The total number of companies in Bloomberg’s database is 1,832,936 of which 66,375 (3.6%) are publicly listed, representing 99% of the world’s market capitalization. However, there is no board information for the majority of non-listed companies, neither for some of the listed companies. The total number of companies with board management information is 98,658 of which 60,631 (61.4%) are public and 38,027 (38.6%) are private. The number of not completely isolated companies amounts to 71,562 in total, divided into 51,256 (71.6%) public and 20,306 (28.4%) private companies. When considering only the largest connected component of C there are 58,352 companies, of which 42,026 (72%) are public and 16,326 (28%) are private.

In total, there are 311,939 board members holding 586,382 board positions, yielding an average number of board positions of 1.87. If completely isolated directors are excluded (that is, members of a disconnected board), 299,982 directors with at least one connection remain. If considering only those directors holding at least two board positions (these are responsible for the links between companies), 102,901 directors remain. In addition to these restrictions, when only the largest connected component (LCC) of D₂ is considered, 85,046 directors remain.

These raw numbers show that engaging in board interlocks is not an activity of public companies only, but rather that there is a strong interaction between them and the private companies. Available records cover companies from 156 countries, but with a high degree of concentration of companies among a small set of them. For instance, more than 90% of the companies are from only 23 countries. The five countries hosting most companies are (in order of their number of companies) the United States, Canada, United Kingdom, Japan, and China.

In the following, we provide some basic network statistics for the overall network and those of some selected countries. Table 1 displays information on the number of nodes and links in the network of companies, the average degree (i.e., number of connections of nodes) , the average shortest path length, the diameter, radius, density, number of triangles and average clustering coefficients. The diameter and the radius are the maximum and the minimum over all nodes of the so-called eccentricity, i.e., the maximum distance between a node and any other. The density gives the number of observed links as a fraction of all possible connections. The number of triangles simply counts the number of triples of nodes that have connections arranged in a circular manner, and the clustering coefficient is defined as the fraction of such observed triangles among the neighbors of a node averaged over all nodes.

Table 1 Number of nodes and edges, average degree and shortest path length ($\bar {L}$), diameter, radius, density, number of triangles and average clustering coefficient ($\bar {C}$) for the LCC of the network of companies C, and for the networks of companies from selected countries

As Table 1 shows, all our networks, national or global, feature the most common indicators of small-worldness: communities, short diameters and average shortest path lengths. In Table 2 we compare the empirical statistics to those of an Erdős-Rényi random network ER(N,M) with the same number of nodes N and edges M as the LCC of C, showing that the empirical number of triangles is several orders of magnitude higher than what one would expect if edges were created randomly between existing nodes. Hence, local clustering (i.e. interlocks) is a pervasive feature of this network (recall that we have at this stage already removed the built-in clustering of the board structures).

Table 2 Comparison between an ER(N,M) random network with the same number of nodes and edges as the LCC of the company network C

4 Measures of Concentration

We are mostly interested in this paper in exploring various dimensions of concentration of links in the global corporate board network that our data identifies. One obvious avenue is to quantify the influence of different countries and different sectors of the economy within this global network. We analyze the relative position of countries and sectors using two different types of statistics: One is the concept of centrality which identifies the relative importance of a node within a network. Here we apply the concept of eigenvector centrality which assigns higher weights to the links between nodes with high centrality scores. The eigenvector centrality of an adjacency matrix A = (a_ij) between a set of nodes is then defined by the equation

$$ Ax = \lambda x $$

(1)

in which λ is the largest eigenvalue which exists and is positive given that A is a matrix with non-negative entries. Note that non-negativity of all elements of the eigenvector is only guaranteed for the one associated to the largest eigenvalue, so that we can only define a non-negative measure of centrality for this eigenvalue (cf. Newman 2008). The k-th element of the eigenvector ν associated with the largest eigenvalue then provides us with the measure of centrality for node k.

Another aspect of interest is in how far the interlocks of a country or sector with other countries or sectors are diversified or not. We measure diversification using the Shannon entropy applied to interlocks of corporate boards:

$$ H(X) = \frac{-{\sum}_{n=1}^{N} P(x_{i}) log(P(x_{i}))}{log(N)} $$

(2)

In our application, N is the number of countries (sectors), and P(x_i) are the relative frequencies of interlocks of a country (sector) with all other countries i = 1,..,N. It ranges from 0 (when all interlocks are with only one specific foreign country (sector)) to 1 (when all connections are evenly distributed across all other countries (sectors)).

Moving on to the specific structure of the overall global network and its subsets, we are interested in whether we can confirm previous results for national board interlocks that have found statistical support for a non-random concentration of economic power in a network “core”. We follow Milakoviç et al. (2010) in testing whether this degree of concentration of positions is statistically significantly different from what one would get under random assignment of director positions to the pool of individuals (which by construction would mean that with X directors assigned to Y board positions and X < Y, a certain number of persons had to end up with multiple positions). This setting suggests as null model the Binomial probability of observing multiple board memberships in an independent sequence of k Bernoulli trials with probability p. The probabilities for observing B = b(b = 1,2,...,B) board memberships of a person is given under the random null model by Eq. 3. In this equation the parameters of the Binomial distribution are the m independent Bernoulli draws for the “excess” in board positions, i.e. m is the overall number of board positions minus the number of directors in the data base, m = Y − X, and p the success probability which is simply the inverse of the number of directors $p = \frac {1}{X}$:

$$ P(B=b)=\left( \begin{array}{c}m\\b \end{array}\right) p^{b}(1-p)^{m-b}. $$

(3)

We support this analysis by a related one which approaches the same phenomena from a somewhat different angle: the so-called rich club coefficient. The rich club phenomenon refers to the tendency of the dominant elements of the system to form tightly interconnected communities (Colizza et al. 2004). Considering the core of corporate networks, the existence of the rich club phenomenon might indicate the presence of a unique group of mutually connected and powerful individuals (or a locus for the interconnection of smaller subgroups), while its absence could suggest the existence of several virtually disconnected (perhaps competing) corporate elites.

The rich club coefficient in networks can be defined as, for a given degree k, the tendency of nodes with degree higher than k to be more densely connected to themselves than to nodes with degree lower than k (McAuley et al. 2007). Formally, it is described as follows: consider a graph with N nodes and M edges representing a complex network. Let N_k be the number of nodes with degree larger than k, and M_k be the number of edges between such nodes. The so-called rich club coefficient ϕ(k) for a given degree k is given by

$$ \phi(k) = \frac{2M_{k}}{N_{k}(N_{k}-1)} $$

(4)

Here again, the statistical significance of possible values of ϕ(k) is an issue: Even in the absence of any systematic rich club tendency, we would expect positivity of ϕ(k) simply because nodes with higher degrees are naturally more likely to be more interconnected as they have more incident edges (Colizza et al. 2004). Indeed, even in the case of the ER graph an increasing rich club coefficient with k can be found. This implies that the increase of ϕ(k) is a natural consequence of the fact that nodes with large degree have a larger probability of sharing edges than low degree vertices. This feature is therefore imposed by construction and does not represent a signature of any particular organizing principle or structure, as it is clear for the ER case. The simple inspection of the trend ϕ(k) is therefore not very informative (Colizza et al. 2004).

The rich club coefficient, therefore, needs to be normalized by its corresponding value in a random graph which follows the same (probably highly skewed) degree distribution. Such a random graph can be generated, for example, by the following randomization procedure described in Milo et al. (2004): take two edges of the empirical network and switch one of their endpoints randomly. If sufficient iterations of this process are carried out, this procedure reshuffles the edge structure of the network but conserves its degree structure. Then the rich club coefficient is computed for the resulting maximally random network, ϕ_ran(k), and it is used to find the normalized rich club coefficient as follows

$$ \rho(k) = \frac{\phi(k)}{\phi_{ran}(k)} $$

(5)

While ϕ(k) gives the rich club coefficient with respect to an ideal uncorrelated graph, ρ(k) is a realistic normalized measure that takes into account the structure and finiteness of the network.

It is worthwhile to stress that the rich club phenomenon does not necessarily have a one-to-one correspondence with a networks’s assortativity (Newman 2002). A positive (negative) assortative mixing implies nodes with high degrees tend to be connected to other nodes of high (low) degree. The fact that these two properties (assortativity and rich club) are not trivially related can be understood by considering a rich club formed by a clique of size four, in which each of the rich nodes is connected to nine other small nodes, as depicted in Fig. 1. This example exhibits the rich club phenomenon together with negative assortativity at the same time. Large nodes are more likely to connect to small nodes than to other large nodes (negative assortativity with respect to degrees), while the inter-connectivity among the large nodes is higher than the connectivity among small nodes (rich club phenomenon).

Fig. 1

Example of a network that combines the rich club phenomena with negative degree assortativity. Large nodes are more likely to connect to small nodes than to other large nodes (negative degree assortativity), while the interconnectivity among the large nodes is higher than the connectivity among small nodes (rich club phenomena)

5 Empirical Results

5.1 Interlocks within and Between Countries

With respect to German board membership data, Milakoviç et al. (2010) point out that the pattern of accumulation of board positions by single individuals cannot be plausibly seen as a chance outcome of random draws from the pool of directors for filling the excess of board positions over the number of directors. Thus, there seem to be systematic tendencies at work responsible for the fact that a small number of individuals assembles a comparatively high number of simultaneous board positions.

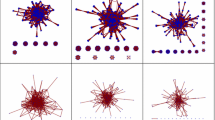
Figures 2 and 3 show the relative frequency of empirical observations of multiple board membership (red circles) and the random Binomial benchmark (blue crosses) of Eq. 3 for eight selected countries. The semi-log scale reveals deviations of increasing orders of magnitude for b > 3, confirming that the characteristic feature presented in Milakoviç et al. (2010) for German data can also be seen for other (both developed and emerging) economies. Figure 4 shows that the same relation also holds for different perspectives on the global network of board members. Figure 2 provides four different perspectives on the global network. In total, there are 311,939 board members holding 586,382 board positions (A), resulting in an average number of board positions of 1.87. If completely isolated directors are excluded (that is, those who are only members of a disconnected board), 299,982 directors with at least one connection remain (B). If considering only those directors holding at least two board positions (these are the ones responsible for the links between companies), 102,492 directors remain (C). In addition to these restrictions, when only the LCC of D₂ is considered, 85,046 directors remain (D). Table 3 presents the number of directors and positions, and the values of m and p for the same selected countries and the global network. In line with the conjecture by Carroll and Fennema (2002), we, thus see that the ‘transnational business community’ is characterized in a similar way as its national subsets by a densely connected core.

Fig. 2

Relative frequency of empirical multiple board membership (red circles) and the random binomial benchmark (blue x’s) for four selected developed countries

Fig. 3

Relative frequency of empirical multiple board membership (red circles) and the random binomial benchmark (blue x’s) for the so-called BRIC countries

Fig. 4

Binomial benchmark and empirical frequencies of multiple board positions. a all directors, b directors with at least one connection, c directors holding at least two board positions, and d only the LCC is considered

Table 3 Number of directors, positions, and values of m and p for eight selected countries and the global network

5.2 The Rich Club Phenomenon

In Section 5.1 above, it has been documented that the frequencies of multiple board memberships are too high both at the international level and for single countries to be explained by random draws. Here we show that there also prevails a general tendency for those with many positions to be connected to others that have many positions, i.e. the existence of a core of highly connected directors that typically serve in multiple boards.

This is the so-called rich club phenomenon introduced above, i.e., some nodes are rich in network ties (they are the hubs) and highly interconnected to each other at the same time (they form a club).

Figure 5 presents the normalized version of the rich club coefficient presented in Section 4 (cf. Eq. 5) for the LCC (largest connected component) of C (red circles) and for the LCC of D₂ (the network formed by board members holding at least two board positions, blue crosses). We indeed find strong indication of the rich club phenomenon over the entire range of k.

Fig. 5

Normalized Rich Club Coefficients for varying degrees for the LCC of C (red circles) and D₂ (blue crosses)

It seems worthwhile to note that this feature is actually enhancing the robustness of a network in the presence of targeted attacks: given the high interconnectivity of the hubs, the removal of one or a few of them would not result in network fragmentation. The rich-gets-richer effect has been mentioned as an explanation for the existence of a very well connected core in the networks of interlocking directorates, as it would result as natural consequence from attaching new nodes to already well connected ones (Buchanan 2003). However, models based on preferential attachment fail to explain the high inter-connectivity present in the core of actual corporate networks.

5.3 The Role of Nations in the International Board Network

In the remainder of this section, a network of countries is defined with countries as nodes, and weighted edges defined by the number of directors holding simultaneous positions in companies from both countries. In this sense, directors whose positions are restricted to companies of the same country are discarded. Figure 6 illustrates this network and its most important actors (nodes are sized and colored by their corresponding eigenvector centralities). The network is composed of 156 nodes (countries), 1,912 weighted edges summing up to 53,074 connections, i.e., there are 1,912 links via board overlaps between countries, and the sum of their weights amount to a total of 53,074 personal connections between directors in different countries. This very dense network shows that in fact all countries represented in Bloomsberg’s data set are connected to some other countries via international board overlaps. We observe that the largest industrialized countries in Europe and North America assume the most central positions together with Hong Kong, China and India.

Fig. 6

Country level aggregation of international interlocks. The weighted connection between two countries is defined by the number of directors holding simultaneous positions in companies from both countries. Directors whose positions are all in companies of the same country are discarded. Nodes are sized and colored by eigenvector centrality

Table 4 presents a different perspective, not based on centrality, but rather on the relation between national and international interlocks.

Table 4 Top and bottom ten and additional selected countries ordered by the ratio between the number of foreign and domestic interlocks, shown in the first column, while the second presents the entropy of the distribution of connections as a measure of how globalized a country is in contrast to strong local connections to only a few other countries

The first column shows the fraction of foreign interlocks over all multiple board positions of directors on the board of any country, while the second shows the normalized Shannon entropy of Eq. 2 of the distribution of connections as a measure of how diversified or globalized a country is in its interlocks with other countries.

Note that H ranges from 0 (when all connections have the same country as an end-point) to 1 (when the connections are equally distributed among all countries). In order to avoid that very small countries (such as Myanmar, Gabon, and Oman) dominate the top of the list (sorted by ratio between foreign and domestic interlocks) only because they have very few companies, we have arbitrarily removed all countries with less than 400 personal interlocks.

The highest fraction of interlocks is observed for smaller European countries: Luxembourg, the Netherlands, Switzerland, and Belgium. However, also larger European countries like Germany, France and Italy are characterized by a relatively high degree of international interconnectedness of their business elite whereas the lower half of the spectrum is exclusively populated by the large Asian countries, the U.S. and Canada. While we would expect a size effect to play a large role in the U.S., the differences between the roughly similar size spectrum of Asian and European countries appears as the most striking outcome of this analysis. Smaller European countries are all characterized by a higher ratio of international than domestic interlocks, which along with a high entropy value (as a measure of diversification of connections), indicates the later are the most open countries as concerns the internationalization of their business elite. Even the larger European countries (France, Germany, Italy, UK) are characterized by a ratio of foreign to domestic interlocks above unity. In contrast, the United States, China, India and the industrial countries of the Far East all are characterized by values below one and smaller numbers of their entropy statistics than the European Union members.

A closely related interesting aspect is the average profile of the firms engaging in international interlocks. Assortativity is the preference of nodes to attach to others that are similar with regard to some attribute (Newman 2002). The classic example is the degree assortativity, given by the Pearson correlation coefficient between the degrees of nodes at either end of the edges. As a correlation coefficient, it ranges from -1 (perfect dissortativity) to 1 (perfect assortativity). Here we consider connectivity wih respect to the country of origin of a board. Since most interlocks often happen within countries, we generally observe positive assortativity with respect to this characteristic. Figure 7 presents the overall country assortativity of the network of companies for varying thresholds of minimum degree, that is, for each degree k the country assortativity is calculated considering only those nodes with degree higher than k. A consistent decrease in assortativity for growing values of k is observed indicating that the higher the number of connections, the higher the chances of engaging in international interlocks. Hence, the more interconnected a board is, the higher the chance that some of its directors will serve on boards in more than one country.

Fig. 7

Country assortativity of the network of companies for varying thresholds of minimum degree, that is, for each degree k the country assortativity is calculated considering only those nodes with degree higher than k. The higher the number of connections, the higher the fraction of international interlocks

5.4 Sector Connectivity

Countries are just one category that could be used to aggregate the entries of our universe of worldwide corporate boards. Another interesting aspect is to differentiate between firms by sectors of economic activity. Table 5 presents the number of positions, directors, and companies by sectors of economic activity. The last two columns show the average number of board positions per director and the average board size. It can be seen that both the banking and the insurance industries are characterized by an average board size significantly higher than the others. There is vast literature supporting the prominent role of financial institutions in the networks formed by interlocking directorates (e.g., Davis et al. 2003). According to Kroszner and Strahan (2001), financial institutions depend more on the business scan than other companies, so for them it should be more necessary to maintain a large number of board connections.

Table 5 Number of positions, directors, and companies by sectors of economic activity. The last two columns show the average number of board positions per director and the average board size in number of positions

Table 6 presents the eigenvector centrality (first column) and the diversity of connections (second column) by sector of economic activity. While the eigenvector centrality shows which are the most central sectors of activity in the network, the diversity of its connections indicates whether the sector is characterized by interlocks only with a few other related sectors or a large part of the network. The diversity of the connections is again defined as the normalized Shannon entropy of the weighted connections. As we can see, the entropy ranges from close to 0 when the sector basically connects to one or just a few other sectors (like Metals & Mining, for example), to close to 1 if the sector connects more or less equally to all other sectors (like Banking, for example).

Table 6 Eigenvector centrality (first column) and connections diversity (second column) by sector of economic activity

The analysis of the role of sectors in the worldwide board network reveals some interesting features: First, the most central sectors are Utilities, Banking and Oil, Gas & Coal, with quite some difference of their eigenvector centrality to the bulk of remaining sectors. In terms of diversity of linkages, we find that most sectors are connected via board overlaps to many other sectors. The pertinent entropy values are hovering around 0.8 − 0.9 in the wide majority of the cases. The only extreme outlier is Utilities, the sector with the highest eigenvector centrality whose entropy is a low 0.226. This is explained by the relatively small sector size compared to the large number of conections it has, both within and between sectors. The last two columns of Table 5 show that theUtilities sector exhibits both the highest average board size and the highest average accumulation of positions by directors among all sectors. In addition, approximately 20% of all linkages in the network of sectors are within the Utilities sector (self-loops), followed by Metals & Mining with 5% and Oil, Gas & Coal with 2%. Utilities also has the highest share of interlocks when self-loops are excluded (3.8%, followed by Banking and Oil, Gas & Coal with 3.1% each).

The central position of the Banking sector is, of course, as expected as the financial industry should have connections to all other sectors due to its service function. Note, however, that its entropy does not appear unusual which speaks against the popular perception that this sector operates as the tacit control center of modern capitalist economies. Drawing on 100 large US industrial corporations between 1969 and 1979, Fligstein and Brantley (1992) hypothesize that interlocks with banks should be positively associated with corporate performance and debt/equity ratios. However, their findings revealed a negative association between bank interlocks and most measures of profitability. In this sense, Mintz and Schwartz (1986) speak about financial hegemony: banks would play a central role in unifying the network of corporations linked through shared directors. In their view, the inner circle of directors with multiple and diverse affiliations, would maximize overall profits, rather than acting in the interest of particular companies. From a different perspective, Ratcliff (1980) points out that no evidence of performance gains by interlocks with the financial sector has been found. Thus, it is argued that the financial institutions are not necessarily central, but different: banks are just special by their very nature in the sense they are holders and distributors of capital.

6 Discussion

The present paper has contributed to the recently burgeoning literature on the network structure of corporate board interlocks. A number of previous studies have already demonstrated that corporate board and director networks exhibit assortative mixing, proximity to a small-world structure and a high concentration of multiple board memberships that would be highly unlikely to occur by chance under sensible null models for the formation of links in the board network. Here we have confirmed this finding using a large international data base. As we have demonstrated in Section 5.1 above, the deviation of the relative frequencies of multiple board positions from a Binomial null model holds not only for a broad range of countries (some of these not covered in previous literature), but it also applies to the worldwide network as a whole. It has also be shown that the subset of directors with large numbers of simultaneous positions exhibits the “rich-club” phenomenon, i.e. they are more closely connected among themselves than other members of the network. Again, this result could be shown to be a highly significant deviation from a random null model, i.e. , even taking into account that a director with multiple positions would by the nature of such appointments be more connected to other directors than a board member with a single position, the high connectivity within the group of high-degree directors is still highly significant. This confirms previous findings for the German board network by Milakoviç et al. (2010) and provides a more rigorous underpinning of their graphical analysis.

Since our analysis is of phenomenological nature, the interpretation of the results in terms of the factors governing board appointments is still open. What we can infer from our results is that there are intrinsic forces in the appointment process that work in favor of a certain concentration of positions in few hands as well as strong connections within the group of directors with multiple memberships. Potential explanatory factors for these tendencies could be economic mechanisms that via signaling of skills make the appointment to another board more likely if a director had already served in one or more positions (Williamson and Cable 2003). Note that this would imply benefits from multiple appointments that overcompensate for the incurred costs of reduced marginal productivity of directors in multiple positions. Besides individual skill, joint board positions could be the result of companies trying to preserve personal relationships along their supply chains or with their main provider of capital and credit in the financial sector. The analysis of the nature of multiple positions in the German economy by Milakoviç et al. (2010) lends very little support to the former hypothesis and somewhat more to the latter.

In contrast to “economic” hypotheses focusing on comparative advantages of busy directors as individuals or advantages in keeping directors busy to secure direct links to important business partners, “sociological” hypotheses would see board interlocks as the consequence of the formation and reproduction of a business elite irrespective of direct economic concerns (e.g. Mizruchi 2000). Evaluations of the influence on economic success of having directors with multiple positions on a company board do not provide convincing arguments for the “economic” viewpoint (c.f. Andres and Lehmann 2010). Some studies indeed provide results supporting the “sociological” view: for instance, Hwang and Kim (2009) show that CEO compensation is higher if there exist social connections between CEO’s and board directors (outside their professional environment), while Nguyen (2012) finds less accountability of the directors if social connections exist. Fracassi and Tate (2012), in addition, document that social connections favor appointment decisions and reduce the monitoring efficiency of the board.

A causal analyses of the factors determining the appointment of directors would require an approach different from the present one. First, a necessary precondition for such a study would be the availability of network data at different points in time. Using dynamic models of network formation (Lusher et al. 2013; Snijders 1996; 2001), one could then attempt to disentangle various factors, from individual determinants (skill), over bilateral characteristics (social ties between incumbent directors and new candidates) to structural characteristics (ensuring interlocks with certain business partners). An example of a study using such a framework is Gygax et al. (2017) who investigate whether board interlocks have an influence on leverage decisions of firms. They find that board overlaps make leverage policies more similar, while existing similarities in leverage strategies are not a determinant of board appointments. Unfortunately, our data are neither of the required dynamic nature, nor do they come with sufficient exogenous information on board members of companies. Nevertheless, moving from the current phenomenological analysis to a causal framework should be high on the agenda of this research area.

7 Conclusion

We have established a number of stylized facts for a large dataset extracted from Bloomberg’s archive of company profiles that should cover to a large extent the segment of large and medium-sized companies of all countries that are integrated sufficiently into the global economy. Our findings confirm previous evidence for national board networks that find a closely connected core around a small set of board members with a relatively large number of positions. Practically the same deviation from a random benchmark is observed for a variety of countries as well as for the entire aggregated network. This supports the view of Milakoviç et al. (2015) of a particular type of self-organization of the board network into a distinctly non-random structure. Since we have confined ourselves to a data-analytical study here, we cannot provide an explanation of this seemingly very robust phenomenon. Given the strong evidence that exists by now on the formation of a closely connected core in board network structures, the analysis of potential generating mechanisms for this emergent feature should be an important task for future research.