Abstract
The analysis of spatial networks’ evolution has predominantly concentrated on the formation process of links. However, the evolution of networks is similarly shaped by the dissolution of links, which has thus far received considerably less attention. The paper presents separable temporal exponential random graph models (STERGMs) as a promising method in this context, which allows for the disentangling of both processes. Moreover, the applicability of the method to two-mode network data is demonstrated. We illustrate the use of these models for the R&D collaboration network of the German biotechnology industry as well as for testing for the relevance of different forms of proximities for its evolution. The results reveal proximities varying in their relative importance for link formation and link dissolution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Network analysis has gained great popularity in many spatial disciplines (Ducruet and Beauguitte 2014). For instance, in urban studies, network analyses are intensively used to study city-networks (Liu et al. 2013), while economic geography focuses on R&D networks’ facilitating of the flow of knowledge between cities and regions (e.g., Murphy 2003; Boschma and Ter Wal 2007). In both fields, studies have sought to explain the evolution of inter-organizational relationships in time and space by relying on longitudinal network data (Broekel et al. 2014). Most of the existing research focuses on the relative importance of factors facilitating link formation. Crucially, network evolution consists of link formation and dissolution processes, though different factors might drive each process. For instance, Balland (2012) noted “[…] that the creation and dissolution of ties are not generally strictly inverse mechanisms […]” (p. 749). Moreover, Krivitsky and Handcock (2014) explained that “social processes and factors that result in ties being formed are not the same as those that result in ties being dissolved” (p. 35). For instance, in order to benefit from scale effects, firms might participate in joint R&D projects with other firms that have a similar technological background (i.e., they are cognitively proximate). Over the course of the project, they realize that their technological similarity stimulates unintended knowledge spillovers, and they end the collaboration to sustain their competitive advantages. Hence, cognitive proximity fostered collaboration in the first place and subsequently increased the likelihood of an early termination of the collaboration. However, while substantial empirical evidence of the first process exists, much less attention has been paid to the second process.
The present paper contributes to the spatial network literature in two ways. Firstly, it demonstrates the use of separable temporal exponential random graph models (STERGMs) as a method for investigating formation and dissolution processes in spatial (knowledge) networks (Krivitsky and Handcock 2014). We apply STERGM to a spatial network emerging from subsidized R&D projects in the German biotechnology industry between the years 1998 and 2013. Secondly, we demonstrate STERGM’s ability to handle two-mode network data, which overcomes the (still) common but sometimes questionable one-mode project of network data when constructing spatial (knowledge) networks (Scherngell and Barber 2009, 2011; Balland 2012; Hoekman et al. 2013; Broekel and Hartog 2013b; Buchmann and Pyka 2015). We thereby extend the work of Liu et al. (2015), who applied a cross-sectional two-mode exponential random graph model to analyze global city networks by presenting an application of ERGMs to longitudinal data. While, alternatively, such data can be investigated with stochastic actor-oriented models (SAOMs) (Liu et al. 2013), these models require specific assumptions (e.g., agency) that are often doubtful in the context of spatial networks (Broekel et al. 2014). In addition, STERGMs have been shown to be empirically similar if not preferable to SAOM models (Leifeld and Cranmer 2015).
This paper is organized as follows: Section 2 discusses the process of an inter-organizational R&D cooperation network evolution. It addresses the relevance of organizations’ attributes, their relational characteristics, and structural level effects. It also considers why existing empirical analyses on their relative importance might be biased, which motivates the use of STERGMs. The STERGM approach is introduced in Section 3. Section 4 discusses the network data and the empirical model specification. The analyses’ results are presented and discussed in Section 5. Section 6 concludes the paper.
2 Disentangling the Determinants of Link Formation and Dissolution in Inter-Organizational R&D Network Structures
On the following pages, we will argue why we expect the influence of factors to vary for formation and dissolution processes, whereby varying effects are particularly likely for proximities and the location.
The literature on the evolution of spatial networks generally highlights three essential levels at which processes of network evolution occur (Glückler 2007; Ter Wal and Boschma 2009; Boschma and Frenken 2010). These levels are the (1) the node, (2) the dyad, and (3) the structural network.
2.1 The Node Level
Many organizational characteristics influence the collaboration behavior of organizations. Researchers have often argued that the size of organizations is of relevance: In particular, two of the expressed arguments are in favor of greater nodes having more links. First, larger nodes, i.e. organizations with more employees, may have greater capacities to establish and maintain more links (Tether 2002). Second, larger nodes tend to attract more requests for interacting, as they usually occupy more prominent positions within specific fields in general and within existing networks (Broekel and Hartog 2013a). For instance, larger organizations are more widely known than smaller ones and, due to their larger portfolio, provide more opportunities for interacting. In case of the Dutch aviation knowledge network, Broekel and Hartog (2013a) found evidence for a positive relationship between size and link formation.
Moreover, larger firms might have more capacities to form new relationships and simultaneously maintain previously existing ones. Smaller firms tend to face a trade-off in this situation — i.e., they must decide whether to invest time in establishing new relationships and giving up existing ones or to opt for maintaining their relations (Tether 2002). Hence, small organizational size might negatively relate to link formation and dissolution, while in case of large organizations, the latter relationship might be positive. This point also highlights that link formation and dissolution are not necessarily independent of each other because of organizations’ potential constraints in their collaboration capacity.
In the literature on spatial (knowledge) networks, organization-specific characteristics (nodes) are complemented by factors at the spatial level, which also impact organizations’ interaction behavior. For instance, Illenberger et al. (2013) hypothesized differences in the relationship structures of individuals living in cities and those in rural areas. While they failed to empirically confirm this hypothesis, empirical evidence exists for organizations in urban and rural areas. For example, Meyer-Krahmer (1985) reported that firms in (urban) agglomerations are more prone to interact with other organizations than firms in rural areas. Broekel and Hartog (2013b) confirmed this positive relationship between population density and organizations’ amount of inter-regional collaboration. Moreover, Wanzenböck et al. (2015) investigated the centrality of regions in inter-organizational R&D networks initiated by the EU Framework Program. Their findings clearly show urban regions being more central in these networks than rural regions. Hence, as an example of a spatial factor influencing organizations’ interaction behavior, we focus on organizations’ location within urban regions, which is expected to facilitate their link formation activities.
In regard to link dissolution, we further argue that these positive urbanization externalities (Boschma and Wenting 2007) will help organizations to maintain relationships. By accessing major train stations and airports, organizations tend to be able to lower transportations costs and will be able to maintain more relationships than organizations situated in more remote rural areas.
-
Hypothesis 1: Organizations located in urban areas are more likely to form a link and less likely to dissolve a link.
2.2 The Dyad Level: How Proximities Shape Network Structures
The dyad level refers to the properties of the relationships between nodes. In research on spatial networks, Boschma’s (2005) proximity framework offers an effective summary of many (specific) arguments made in the literature. Among others, the concept builds upon the homophily effect, which has been applied in sociology. Here, it is argued that two individuals are more likely to develop a trust-based relationship when they share similar attributes (e.g., the same age) (McPherson et al. 2001). This concept has been transferred to the organizational and regional levels as well as to other types of relationships and similarities. More precisely, Boschma (2005) summarized the prominent arguments in the literature and proposed a distinction between five dimensions of inter-organizational proximities. These proximities describe organizations’ similarity (homophily) in different dimensions and are all argued to increase the likelihood of two organizations to establish a (collaborative) relationship and to exchange knowledge. These proximities are cognitive, geographical, organizational, social, and institutional.Footnote 1 As our empirical analysis will focus on cognitive, institutional, and geographic proximity, we limit the theoretical discussion to these dimensions. A discussion on the other two dimensions can be found in Boschma (2005).
Nooteboom et al. (2007) defined cognitive proximity as the result of organizations’ development of an organization-specific internal “interpretation system” (Ibid: p. 1017). At its core is the organizations’ absorptive capacity. As learning is a cumulative process that builds upon existing knowledge, their absorptive capacity increases when new and previously possessed knowledge overlap (Cohen and Levinthal 1990). Accordingly, organizations tend to interact with partners who share similar knowledge bases. In this case, it is easier and more efficient for organizations to identify them as potential collaboration partners, absorb their knowledge, and jointly learn (Nooteboom et al. 2007). The positive impact of cognitive proximity on link formation in spatial R&D networks has been frequently confirmed (Paier and Scherngell 2011; Balland 2012; Broekel and Hartog 2013b; Buchmann and Pyka 2015).
While cognitive proximity greatly increases link formation, two cognitively similar organizations are likely to be competitors because they tend to produce similar products (Boschma 2005). This circumstance increases the risk of withholding knowledge in order to avoid unintended knowledge spillover (Zander and Kogut 1995). Moreover, given their cognitive overlap, these organizations offer relatively little to learn from each other. In such a situation, the formed alliance may be unstable (Polidoro et al. 2011), as organizations tend to be reluctant to stay in alliances longer than necessary. Accordingly, cognitive proximity may increase the chances of early link dissolution.
Geographical proximity refers to the “similarity” of organizations in terms of their geographic location. Being geographically close or within the same region fosters the formation of links because it makes frequent face-to-face interactions much easier (Boschma 2005). Such contacts facilitate the generation of mutual trust and are especially important when exchanging tacit knowledge (Ter Wal 2014). In spatial sciences, geographical proximity is a key interest and thus is often analyzed in regard to network formation. For instance, in the case of funded R&D networks, Paier and Scherngell (2008) and Balland (2012), among others, have found evidence of a positive relationship between link formation and geographical proximity.
As geographic proximity strongly enhances the possibility of frequent face-to-face contacts and more insightful communication, it may contribute to the earlier completion of projects, which in turn will result in quicker link dissolution. It might even be the case that partners anticipate the higher efficiency and more effective communication when collaborating in geographic proximity and therefore opt for shorter project durations when setting-up collaborations with geographically proximate partners, such as when applying for joint grants.
-
Hypothesis 2: Geographic and cognitive proximity positively influences link formation and dissolution.
Institutional proximity is also associated with the embeddedness literature, i.e. organizations operating in different social subsystems (e.g., industry or academia). According to Ponds et al. (2007), scientific research and the development of product innovations are “conducted within different socio-economic structures” (p. 426). Institutionally distant organizations are more likely being confronted with unknown behavior and problems in mutual communication, which reduces the likelihood of interaction (Parkhe 1991; Boschma 2005; Balland et al. 2013). Institutional proximity ensures that partners operate under the same or at least comparable institutional (legal and societal) frameworks, which significantly aids in overcoming the risks of freeriding and reduces monitoring costs (Boschma 2005). Accordingly, it strongly helps with initiating collaborations, which is also empirically confirmed (Balland 2012).
In contrast, its relevance for link duration might be rather minimal. It can be argued that once collaboration has been initiated and formalized, most legal and formal issues concerning the collaboration are settled and contractually fixed. While the efforts needed for this may prevent the formation of interactions, the institutional frameworks may become complementary through the formal contract and, hence, exercise little to no effect on link duration.
-
Hypothesis 3: Institutional proximity impacts link formation positively but does not affect link dissolution.
2.3 Structural Level Determinants
Glückler (2007) and Liu et al. (2015) highlighted the relevance of factors at the structural network level. These authors argued that a theory of network evolution focuses on the interdependency of new links and the overarching structure of the network as such. Accordingly, “[…] this perspective explicitly moves beyond the dyadic analysis of single relationships to the analysis of entire network relations” (Glückler 2007: p. 622). Three factors have received the most attention so far: triadic closure, multi-connectivity, and preferential attachment (Glückler 2007).
Triadic closure implies that partners of a node are likely to become partners themselves. This is shown by so-called triangles in networks, i.e. dense cliques of strongly interconnected nodes (Ter Wal 2014). In spatial (knowledge) networks, such cliques are usually interpreted as a sign of social capital (Coleman 1988), which may enhance trust and the willingness among nodes to invest in mutual goals. For instance, Ter Wal (2014) confirmed the relevance of triadic closure for the evolution of a biotech network based on co-invented patents.
Multi-connectivity is a consequence of organizations tending to seek a diverse portfolio of partners. In other words, they may connect to others in multiple ways to decrease their dependency on individual links (Glückler 2007). For example, organizations may link to other organizations through joint R&D projects in addition to existing buyer-supplier relations. Broekel and Hartog (2013a) provided empirical evidence for the relevance of such processes in the context of subsidized spatial networks.
Preferential attachment implies that the probability of creating additional links may increase with every new link a node possesses (Vinciguerra et al. 2010; Liu et al. 2015). Organizations with many relationships tend to have a greater flow of information about new activities and partners, and they also tend to have a stronger ability to evaluate these by means of collaborative behavior and appropriate resources (Polidoro et al. 2011). While Broekel and Hartog (2013b) hypothesized preferential attachment to play a role in networks of subsidized R&D collaboration, they failed to empirically confirm this. With respect to their relevance on link formation and dissolution, the literature clearly suggests a positive contribution to link formation, while discussions on their effects for link dissolution are largely absent. We therefore expect that their positive influence is also applicable to link persistence (i.e. these effects are negatively correlated with link dissolution).
-
Hypothesis 4: Network structures support link formation and suppress link dissolution.
3 Separable Temporal Exponential Random Graph Models
A range of methods can be applied to identify factors driving networks’ evolution (see, for example, a recent review of the most common approaches: Broekel et al. 2014). In the context of dynamic spatial networks, SAOM models in particular have been used (Balland 2012; Liu et al. 2013). These models are convincing due to their wide range of application possibilities, consideration of factors at all three levels of investigation, and usability with one and two-mode network data. While their applicability and functionality were unmatched in the past, the development of the TERGM (temporal exponential random graph model) and STERGM (separable temporal exponential random graph model) provides researchers with a legitimate modeling alternative. It is beyond the scope of the present paper to conduct a full review and an empirical comparison of the two models. For this, we refer to Broekel et al. (2014) and even more so to Leifeld and Cranmer (2016). The paper instead focuses on an application of the recently developed STERGM and seeks to highlight its three most prolific features that are crucial in the context of spatial (knowledge) networks: its nature as a tool of dynamic network analysis, its applicability to two-mode network data, and its ability to separate formation and dissolution processes. While SOAMs offer similar features, these are achieved by the fundamental assumption of agency residing with the nodes. In other words, the models are built on actor-based behavioral assumptions (Park and Newman 2004). When applying these models to inter-organizational or inter-regional networks, this assumption of agency is likely to be violated (Broekel et al. 2014). Moreover, recent theoretical and empirical comparisons suggest that (S)TERGMs outperform SOAMs (Leifeld and Cranmer 2015), which further motivates the presentation of STERGM for the analysis of spatial (knowledge) networks.
The separable temporal exponential random graph model (STERGM) is a recently developed extension of the exponential random graph model (ERGM) (Krivitsky and Handcock 2014); as such, it is part of the ERG family (also known as p*-models (Robins et al. 2007)).
As neither nodes (actors) nor dyads (relationships) are completely independent from each other, classical econometric models such as regression analysis do not effectively explain the structure of observed networks (Broekel et al. 2014). For that reason, Frank and Strauss (1986) developed the so-called Markov dependence on which ERGMs are based. It implies that a given dyad between two actors impacts and is impacted by any further link of those two actors (Robins et al. 2007). Therefore, links are defined as being “conditionally dependent” (Ibid: p. 181).
Models of the ERG family consider link creation as a continuous process, and the observed network structure is seen as one possibility out of a large set of potential networks with similar characteristics (Robins et al. 2007). This range of possible network patterns and their likelihood of appearance “is represented by a probability distribution on the set of all possible graphs with this number of nodes” (Ibid: p. 176). Hence, a good ERGM has a high probability of simulating the observed network by finding the correct coefficients of the determinants impacting the network structure. For this purpose, a Markov chain Monte Carlo maximum likelihood estimation (MCMC MLE) procedure is used to simulate and evaluate the modeling process (Broekel et al. 2014).
Mathematically, an ERGM is defined as follows (Robins et al. 2007):
where Pr(Y = y) is the probability that the observed network (y) equals the simulated network (Y). The network configuration A is considered by ηA, and the network statistics are represented by gA(y). The network configurations are the determinants with which the researcher attempts to explain the network structure, such as cognitive proximity. ERGMs allow the inclusion of node, dyad, and structural determinants at the same time (Broekel et al. 2014). gA(y) is either 1 if the configuration is observed in y, or 0 if it is not. The factor κ is a normalising constant that is implemented to ensure a proper probability distribution of the equation (Robins et al. 2007).
Hanneke and Xing (2007) and Hanneke et al. (2010) extended the ERG family with a framework that enables the researcher to model network dynamics over discrete time steps, called temporal ERGM (TERGM). In this model, a network at time t is conditional on the network at time t - 1. In essence, the TERGM corresponds to a stepwise ERGM approach with the steps corresponding to the observed time periods (Krivitsky and Handcock 2014). Recently, Krivitsky and Handcock (2014) built upon this model and introduced the concept of separability. This allows a STERGM to independently consider the process of link formation and dissolution. In consideration of the organizational processes underlying the establishment and maintenance of cooperation, it seems legitimate to view different factors as in control of link formation and dissolution. A STERGM displays the transition from one time period (t) to the following time period (t + 1) and thereby independently analyses the formation and dissolution of links. Accordingly, a STERGM is separated into two formulas (Ibid.). One formula considers the formation of links:
The other formula considers the dissolution of links:
The general aim of this method is to obtain a model with a high probability of simulating the observed network and that can identify the best coefficients. The success of the simulation can be tested by checking whether the model is degenerated and by examining the model’s goodness of fit. A degenerated model is often the consequence of misleading starting parameters and/or variables that are not able to correctly simulate the observed network. A degenerate model does not converge or the calculated estimates simulate a network that is either extremely dense or has almost no edges (Robins et al. 2007).
A non-degenerated model has to be further tested regarding the quality of simulating the observed network. By comparing the network characteristics of the simulated network (e.g., the degree distribution) with the corresponding statistics of the observed network, the goodness of fit can be verified graphically (Hunter et al. 2008).
When calculating several models of the same size but with slightly different variables, the Akaike information criterion (AIC) and the Bayesian information criterion (BIC) provide additional information on a model’s goodness of fit. However, by including several network configurations (variables), the model becomes increasingly complex, and both AIC and BIC become less precise (Goodreau 2007). Therefore, they should only be used in combination with the graphics mentioned above.
We take advantage of the STERGM being capable of handling two-mode data. Accordingly, a one-mode projection is not necessary, but we directly analyze the two-mode structure of the network. In this case, the researcher must make sure that the simulation procedure does not create links that are impossible, i.e. no links should be simulated among events or among participants, only between events and participants (for practical application see Morris et al. 2008 and Section 4.4).
4 Empirical Approach and Data
4.1 Data
The empirical network is based on organizations’ participation in joint R&D projects subsidized by the German Federal Ministry of Education and Research (BMBF), the Federal Ministry of Economics and Technology (BMWi), and the Federal Ministry of the Environment, Nature Conservation and Nuclear Safety (BMU). Data on subsidized R&D projects are extracted from the so-called “Förderkatalog” (subsidies catalogue).Footnote 2 Financial support for joint R&D projects is conditional on all participants agreeing to exchange knowledge with each other. Moreover, they grant access to intellectually property rights that are within the scope of the project but existed before project’s start (BMBF 2008). Therefore, inter-organizational relations based on joint participation in such subsidized projects qualify as knowledge exchange links (Broekel and Graf 2012). The data consist of firms, universities, and research institutes that operate in the German biotechnology industry and obtain subsidies for their joint projects in the period from 1998 to 2013.
The industry has been chosen because it can be classified as a science-based industry in which scientific advancements primarily drive economic progress (Ter Wal 2014). Moreover, cooperation is essential for innovation in this industry, as its “locus of innovation” is located in the network of inter-organizational relationships rather than in a single organization (Powell et al. 1996: p. 119). Thus, inter-organizational R&D cooperation is an important competitive factor in the biotechnology industry because individual firms may not be able to cover all of the necessary capabilities to innovate (Ibid).
Regarding the economic entities being used as nodes in the network analysis, the subsidies catalogue distinguishes between the beneficiary unit (“Zuwendungsempfänger“) and the executing unit (“Ausführende Stelle“). The first refers to the receiving organization (e.g., organizations’ headquarters), and the latter refers to the executing entity (e.g., a specific department or an institute of this organization). In accordance with the literature (Broekel and Graf 2012), we chose the executing units as network nodes because they actively select whom to cooperate with and decide when to end a project.
4.2 The Structure of Two-Mode Networks
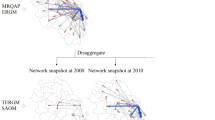
The described data represent a two-mode (or bipartite) network, as actors are related to projects and not directly to other actors. We extracted 652 nodes at the actor level (mode 1; i.e., organizations) and 258 nodes at the event level (mode 2; i.e., projects). Both levels are connected through 1177 links (see Fig. 1). The two-mode network structures have significant implications for network analysis, as, for instance, network structures such as closed triads are not possible.
To account for factors’ importance varying over time (see, e.g., Balland et al. 2013), we split the network into four phases, with each being 4 years (see Fig. 1 and Table 1). We defined a link to be formed when a project started within the observed time phase. It was maintained when the project had not been ended during the foregoing timespan. Otherwise, the link was been dissolved (see Fig. 2). Pooling the data for 4 years caused the resulting networks to be sufficiently dense. We analyzed the three transitions of the networks from one period to the next by estimating separate models for each transition. This allowed for assessing potentially time-varying effects of our explanatory variables.
The STERGM demands the network to have the same set of nodes in both time periods. This gave us two opportunities: First, we could have included all nodes in the networks, regardless of whether they have a link in that period. However, this would have led to more complex models and would have decreased the chances of a converging model. Moreover, nodes only participating in the first transition are irrelevant for the following transitions. Therefore, we went with the second possibility: In the first STERGM, we only considered nodes that participate in the first and second periods. In the second STERGM, we then only included nodes participating in the second and third periods. Finally, in the third model, we only considered nodes that had a link in the third or fourth period. Eventually, we had two slightly different networks for the second period and the third period (see Table 7 in the appendix for an overview of the networks).
In the case of publicly subsidized project data, multiple reasons may exist for the dissolution of links. First, if participants successfully complete the project within the subsidized time period, the network link(s) will disappear. Second, if organizations apply for and receive a second funding within the project run-time, the link will be extended without a break, and we would not observe the dissolution of a link. Interestingly, we did not find a single instance in which this took place. We speculated that a policy discriminates against immediately reoccurring project partnerships when awarding new grants. Third, a policy could artificially induce the termination of joint projects and the according dissolution of network links, thus setting a maximum project duration. While this motivated Balland (2012) to argue that “analyzing why links are dissolved […] in the case of projects whose length is fixed from the beginning seems less relevant” (p. 749), we argue that partners know about fixed project durations ex-ante. Hence, they will apply for a grant only if its duration meets the (foreseeable) requirements of the planned project, which includes the consideration of the scope, complexity, and partner characteristics. Each of these considerations is usually known ex-ante to some extent. Similar to Makino et al. (2007), we therefore expected the initial conditions of partner selection to influence the projects’ length. For instance, we expected more complex (and therefore longer) projects to more likely involve geographically proximate partners, as the complexity requires more frequent face-to-face contacts (see, e.g., Balland and Rigby 2016). Similarities can be expected for projects involving actors at greater cognitive distances, which also tend to demand increased and closer interaction (Boschma 2005). Two processes are likely to support this. Firstly, when designing subsidization programs, a policy is probable to consider the task’s complexity and defines longer project durations. Secondly, applicants may look for programs with maximal project durations that fit the complexity of the expected task. We assumed project-lengths are (indirectly) related to the type of partners and consortia applying. Significant results in the dissolution models will show the extent to which this assumption is valid.
Based on these arguments and secondary data, we constructed the following variables at the node, dyad, and structural network levels.
4.3 Dyad Level Variables
Categorical and binary dyad-level effects are considered in the STERGM by evaluating how frequently two-paths are created between two organizations sharing the same characteristics (see Fig. 3). We were thereby particularly interested in their characteristics concerning cognitive, geographical, and institutional proximity. We did not consider social and organizational proximity because of missing data.Footnote 3
In the biotechnology industry, organizations are commonly assigned to a technological subfield: medicine and pharmacy, industrial processes, agriculture, and (bio)informatics (DaSilva 2012). These fields represent distinct technological foci and systematic differences in the way R&D is conducted (Herrmann et al. 2012). We constructed a simple measure of cognitive proximity based on this assignment. If two partners were assigned to the same category, they were perceived of as being cognitively more proximate than in the case they were active in different technological subfields. The variable COG PROX was given a value from 1 to 4 according to the assigned subfields.Footnote 4
The measure of geographic proximity (GEO PROX) is a categorical variable corresponding to the NUTS 3 region in which organizations are co-located. In Germany, NUTS3 regions correspond to 429 districts (Kreise), which are administrative areas ranging from cities such as Munich or Berlin to rural areas such as the Uckermark in East Germany (for additional figures, see Table 2).
Moreover, organizations were classified as being profit orientated (private firms) and as non-profit organizations (universities, research institutes, and associations). This difference was captured by our measure of institutional proximity (INST PROX), which is categorical and distinguishes between firms (0), universities (1), and research institutes (2).
4.4 Organizational Node Level Variables
Potential location effects of organizations situated in urban areas were approximated using data of the Federal Institute for Research on Building, Urban Affairs and Spatial Development. It classifies each German NUTS 3 regions as “urban,” “increasing urbanization,” or “rural.” The classification is based on the total population and population density (BBSR 2015). We constructed the categorical variable (URBAN) as 0 for rural, 1 for increased urbanization, or 2 for urban regions.
The second variable at the node level approximated the size of organizations. As it was impossible to acquire the number of employees for each organization and year, we created a categorical variable (SIZE) indicating membership in different size classes. SIZE consisted of the categories utilized by the Reconstruction Credit Institute (KFW (2012) as well as Buchmann and Pyka (2015):
-
Category 0: organizations with fewer than 50 employees.
-
Category 1: organizations with 51 to 250 employees.
-
Category 2: organizations with more than 250 employees.
The third node level variable is EAST, which distinguishes organizations located in West (Category: 0) and East Germany (Category: 1). To the catching-up process of the East German economy, a large share of European and German subsidies is allocated there to facilitate this process. Thus, there might be a propensity to favor applications from organizations being located in cities formerly belonging to the German Democratic Republic (GDR). Moreover, Cantner and Meder (2008) discovered that East German organizations participate more actively in R&D collaborations.
As we sought to model interactions between specific variables (see Section 4.3.), we also considered the corresponding main effects at the node level. We therefore included node-level variables consisting of the categories of cognitive proximity (i.e., MEDICINE and AGRICULTURE with base INDUSTRIALFootnote 5) and the differentiation between types of organizations (i.e., UNI and RESEARCH INST with base FIRM).Footnote 6 While surely being interesting on their own, due to the scope of the study, we primarily included these variables as control variables.
4.5 Structural Level Variables
At the structural level, four variables were considered.Footnote 7 The effect of multi-connectivity was captured by the so-called geometrically weighted dyad shared partner statistic (GWDSP). A positive coefficient of this statistic suggests that actors tend to link in multiple ways (i.e., via multiple projects) to each other (Hunter et al. 2008).
The second structural determinant is preferential attachment. We modeled this by making use of the variable GWDEGREE, which represents the geometrically weighted degree statistic. The variable is seen “as a sort of anti-preferential attachment model term” (Hunter 2007: p. 7). If its coefficient is negatively significant at the actor level,Footnote 8 preferential attachment is a likely driver of network evolution. In contrast, there is no clear interpretation of a significant coefficient of GWDEGREE at the event level. It means that preferential attachment works at the project level, which lacks a theoretical foundation. Nevertheless, the effect was included to help the simulating of the network.
The observed networks are characterized by high numbers of projects with three participants (see Fig. 2). We considered this by including the variable B2DEG3, which added a statistic to the model counting how frequently B2-nodes (projects) have three links, i.e. three participants (Morris et al. 2008).
The final structural network variable is EDGES. This variable should always be included when modeling a network with any ERG method. It equals the number of observed edges and helps in modeling the density of the observed network in the simulations (Broekel and Hartog 2013b).
In the appendix, Table 6 presents the descriptives of all node and dyad level variables.
5 Results and Discussion
5.1 Verifying the Model
Before presenting the empirical results, it is important to address a number of issues that have to be taken into consideration before interpreting the results. For instance, there might be a potential bias connected to our data. For historic reasons, subsidized R&D projects frequently (but not exclusively) have a length of 36 months (see Fig. 4).
Accordingly, project lengths are not fully flexible, and organizations do not have full freedom in choosing a support scheme allowing for project lengths that meet their requirements (also see Section 2). In other words, this precondition dominates link dissolution. To evaluate the significance of this, we created a second network that eliminated all links of projects that terminated immediately after 36 months. Projects and participants that became isolates because of this circumstance were also deleted. The corresponding network consisted of 144 projects and 476 actors.
There are two implications. Firstly, due to the predefined project lengths, we were less likely to obtain significant coefficients in the dissolution model, as project endogenous processes and conditions are “overruled” by these externally imposed conditions. In other words, link dissolution becomes an external event and hence cannot be explained by endogenous processes. Secondly, if significant coefficients are obtained or differences between the models for the full set of projects and those excluding links of 36 months are observed, these should be primarily interpreted as selection effects — i.e., partners choose specific support schemes considering the maximal time of subsidization when applying for grants.
In general, the results do not change significantly when excluding the 36-month projects, which indicates, similar processes drive both networks’ evolution. A major difference is related to geographic proximity. It was not possible to find a converging model when considering the full set of projects. However, when excluding the 36-month projects, convergence was achieved, and we obtained reliable results.
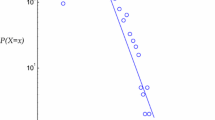
Besides convergence, STERGM involves finding the best model in a manual iterative trial-and-error process (Broekel and Hartog 2013b). Usually, a first estimation is used to calculate starting values entering the second estimation (similar to Goodreau 2007). The models’ goodness of fit is assessed via the degree distribution. Figures 5 and 6 plot the observed network’s degree distribution as a solid line and the 95% confidence interval of the distribution for the corresponding simulated networks as box-plots and light-grey lines. A solid line within the light-grey lines represents a model with a satisfying goodness of fit (Krivitsky and Goodreau 2015). The figures reveal our models as being of sufficient overall quality because only small parts of the simulated degree distribution exist outside of the observed one (Krivitsky and Goodreau 2015).
The coefficients of the formation and dissolution model can be understood as odd ratios by taking the exponential. In the case of the formation model, a positive coefficient means that the establishment of a link is more likely. In contrast, in the dissolution model, a positive sign signals persistence of a link, i.e. the lower likelihood of dissolving (c.f. Krivitsky and Goodreau 2015).
5.2 Factors Driving the Formation of Links
The results of the formation model are presented in Table 3. The model with all links (initial) and the model excluding the 36-month links (refined) are very similar and do not contain conflicting results. However, the initial model contains more significant coefficients and therefore serves as a basis for the interpretation.
At the node level, INCR URBAN, and URBAN are significantly negative in Model 2, which indicates that in the second period (2002–2005), rural organizations participate in more joint projects than urban ones. The variable is insignificant in the other models. The results are not in line with Hypothesis 1, which suggests urban organizations being more likely to form links due to urbanization externalities. We suspect an effect similar to what Illenberger et al. (2013) found for individuals. Organizations might compensate for the lower accessibility of partners with the higher acceptance of partners in rural areas. Alternatively, after the BioRegio initiative ended in 2005 (see, e.g., Dohse 2000), support became less focused on urban regions, and rural regions gained importance in subsidization schemes. In any case, Hypothesis 1 is not confirmed, as organizations in urban regions are not more actively engaging in subsidized R&D collaboration than rural organizations.
SIZE1 and SIZE2 obtain significantly positive coefficients in Model 1 and Model 2, respectively. Accordingly, medium-sized and large-sized firms have higher probabilities of link establishment in comparison to small firms (fewer than 50 employees). This fits with our line of argumentation in Section 2.1 regarding larger firms having more capabilities and opportunities to establish links. Our findings are in line with the results of Tether (2002), who argued that larger firms might benefit from their size in two ways: First, they are more attractive for cooperation partners (e.g., universities), and, second, they might force their suppliers into cooperation projects.
The coefficient of EAST is significantly positive in Model 1. This supports the findings of Cantner and Meder (2008) — specifically, that East German organizations are more active in subsidized R&D-cooperation, which corresponds to the idea of a policy’s stronger support for these regions.
At the dyad level, we found that COG PROX was significantly positive in all models. Organizations operating in the same subfields of biotechnology are more inclined to conduct joint R&D. Accordingly, Hypothesis 2 is confirmed, and our results add to the findings of Nooteboom et al. (2007) and Balland et al. (2013), showing that cognitive proximity is an important driver of R&D network formation.
In addition to cognitive proximity, geographic proximity also plays a significant role in the formation of R&D cooperation. GEO PROX obtained a significant coefficient in the second refined model but remained insignificant in the first and third models.Footnote 9 Thus, in the second period, organizations tend to work together with partners located nearby, which supports Hypothesis 2.
Institutional proximity (INST PROX) is significantly positive in the first formation model, suggesting that organizations with the same institutional background are more likely to work together. Hypothesis 3 is thereby confirmed. Due to less uncertainty regarding partner goals and behavior, organizations tend to select cooperation partners from the same institutional background (Ponds et al. 2007).
Only one of the findings on variables at the structural level is in line with our expectations. All other factors excluded, the variable EDGES represents the density of the network and can be interpreted similar to an intercept. As the observed network is the consequence of a social process, it is typically less dense than exponential random networks leading to the negative coefficient of EDGES (Varas 2007).
Unexpectedly, GWDSP was significantly negative in all of the models. This contradicts the multi-connectivity proposition of organizations’ tendency to connect through several ways in order to decrease link dependencies. In our case, organizations rarely engaged with the same organizations in multiple subsidized R&D research projects, which appears to be a valid, but still unexpected, strategy to maximize learning and inter-organizational knowledge diffusion. While a potential explanation might be a policy penalizing collaborations of the same organizations in its subsidization programs, we are not aware of such a rule.
GWDEGREEB1’s coefficient gained a significantly sign; however, its sign is positive, which contradicts the preferential attachment process (Hunter 2007): Organizations are less likely to gain additional links when they are already well connected. We clearly must reject Hypothesis 4 with respect to the link formation model. There are three potential reasons for this: Firstly, organizations are limited in their collaboration capacities, thus implying that they constantly face a trade-off between maintaining and acquiring new links through projects. Similarly, they might not have the capacity or willingness to apply to multiple subsidization programs within the same time period. Secondly, subsidization programs are more focused, and there is only a limited overlap between organizations’ activity portfolios and support programs. Thirdly, a policy might favor subsidizing a broad range of organizations and therefore penalizes organizations already active in a large number of projects.
5.3 The Dissolution Models
As expected (see Section 5.1), we found fewer significant coefficients for the dissolution models (see Table 4). We believe that this is due to the relatively low variance in link duration, which is strongly constrained by the design of the underlying policies (5.1). Nevertheless, as argued in Sections 4.1 and 5.1, significant results are still possible and interesting.
The coefficient of RESEARCH INST is significant and negative in Model 3. This finding implies that research institutes are either leaving projects earlier (unlikely) or initially opting for shorter projects (more likely) than firms. As research institutes are inclined to exchange knowledge with diverse sources (Ponds et al. 2007), shorter collaboration appear to be more attractive to these organizations. This also allows for the establishment of a diverse network of collaboration partners and for the maximizing of access to knowledge from different subfields. The same argument can be brought forward regarding universities. However, it might also be the case that both types of organizations relate their R&D projects to the completion of PhD theses (which usually require about 3 years) and therefore target the 36-month projects. In the case of universities, some support for this can be found in period 3, in which the coefficient is positively significant. In other words, once the 36-month projects are excluded (which are likely to relate to PhD projects), universities are less likely to be engaged in shorter projects and collaboration.
In the Model 3, INCR URBAN is significantly negative, meaning that organizations located in urban areas are more likely to dissolve links in comparison to organizations in rural areas. Again, there might be multiple explanations for this. Organizations in urban regions are known to have a large selection of (nearby) potential collaboration partners, which organizations in rural regions lack (Meyer-Krahmer 1985). Accordingly, they might be more interested in shorter projects in order to exploit and thereby make use of this potential. Organizations in rural regions might also be less attractive collaboration partners because of lower reachability, less prestigious names, etc. This lack of attractiveness has to be compensated by larger subsidies, i.e. larger and longer R&D projects. Additionally, organizations in urban and rural regions might have different technology foci. Shorter projects are more attractive for organizations seeking to remain at the technology frontier, which implies making quick progress and constantly exploring new developments on a short-term basis. However, organizations in rural regions are less likely to be active in the most recent and most complex technologies (Hägerstrand 1967; Balland and Rigby 2016). Hence, shorter projects are not as attractive for them, thus leading to lower link dissolution probabilities. Future research should more thoroughly address this issue, such as by applying qualitative methods.
We also determined that the dyad-level variable INST PROX was negatively significant in the second model. This contradicts Hypothesis 3, in which we argued that institutional proximity is unlikely to influence link dissolution. Here, the negative sign inclines partnerships between profit and non-profit organizations to last longer than between profit and profit organizations and non-profit and non-profit organizations. A straightforward explanation is that projects involving partners with different institutional backgrounds require more time (and hence apply for longer projects) than partners operating within the same institutional framework (Boschma 2005).
At the structural level, EDGES and GWDEGREEB2 were highly significant in all the models. EDGES is interpreted as in the formation model with its significantly positive coefficient pointed toward higher network density than in a random network. The effect of preferential attachment is also present in the duration of links. The significantly positive coefficient of GWDEGREEB2 implies links established between new organizations and projects that are already well embedded in the network are less persistent. We interpret this as being primarily a technical effect. Projects and organization in the network that hold central positions do so because they are participating in large projects. Note that we established earlier that few organizations are active in multiple projects at the same time. Hence, when the project is completed, they will lose most if not all their links at the same time. This number will naturally be larger than in case of less central organizations and projects (because otherwise their centrality would not be lower). Accordingly, prominence in the network caused by participation in larger projects (in terms of the number of participants) tends to imply larger dissolution rates of links. The results for the other structural network variable GWDSP are inconclusive as its coefficient alters between the models. Again, we have to reject Hypothesis 4, network structural effects do not relate in the expected way to the evolution of the network. This is most likely, partly caused by the endogenous dissolution processes, which are strongly impacted by the (externally fixed) conditions of the support programs.
6 Conclusion
In urban studies and related fields, dynamic network analysis has become a crucial tool to understand the evolution of different types of networks in time and space. In particular, studies analyzing spatial knowledge networks have increasingly relied on dynamic network analysis (Boschma and Martin 2010; Glückler 2007; Glückler and Doreian 2016; Ducruet and Beauguitte 2014). Interestingly, most existing studies have thereby focused on the formation of links. However, as Glückler (2007) put forward, network evolution is a twofold procedure that “should be conceived as the result of endogenous mechanisms of network formation and dissolution” (Ibid: p. 627). Accordingly, in order to fully understand the evolution of spatial networks, both processes need to be considered in empirical investigations.
The paper contributes to the literature by discussing the separable temporal exponential random graph model (STERGM) as a novel and interesting tool in this context. We demonstrate its use for the analysis of the evolution of spatial (knowledge) networks by presenting a case study on the (subsidized) R&D collaboration network of the German biotechnology industry. In particular, we highlight the STERGM’s capacity to directly analyze two-mode networks, which avoids the sometimes questionable one-mode projection (see also Liu et al. 2015). In addition to the dynamic analysis and the possibility of disentangling formation and dissolution, this feature was frequently argued to be the primary benefit of using stochastic actor-oriented models (see, e.g., Liu et al. 2013).
Besides advocating the use of the STERGM, the paper also aimed at exploring the roles played by location (urban – rural) and different types of proximities (cognitive, institutional, geographic) for the formation and dissolution of spatial knowledge links, with the latter having received little attention in the past.
Table 5 provides an overview of the main results. Overall, the results of the formation models are in line with the theoretical expectations. Interestingly, the same cannot be said for the dissolution models. In these cases, we were not able to find solid evidence for location and the proximities to strongly impact link dissolution.
However, we observed that these factors seem to vary in their influence on formation and dissolution. If we expand our view beyond our relatively narrow hypotheses, we find confirmation for variations in the relative importance of factors for link formation and dissolution; some factors are more crucial for the formation while others impact link dissolution to a greater extent. For instance, institutional proximity, i.e. whether organizations cooperate within the same (university, applied research, or profit) framework, makes link formation more likely. At the same time, it also facilitates link dissolution. Accordingly, simply inferring from knowledge on formation processes on dissolution dynamics is invalid, and we need to analyze both processes separately.
Our results also show that factors’ influence on network evolution is not time-invariant but is instead conditional on the current framework in which an industry operates. While previous studies argued for the relevance of industry life-cycle phase and thereby endogenous conditions (Balland et al. 2013; Ter Wal 2014), our analysis (due to the nature of the employed data) highlights the relevance of external circumstances — in this case, variations in the R&D policy.
As is typical for empirical studies, our case study used for demonstrating the applicability of STERGM is subject to certain limitations. First, the STERGM was only recently developed, which implies some shortcomings that will certainly be addressed in the future. Currently, continuous variables at the dyad level are difficult to implement. This is particularly relevant in the context of spatial networks as geographic proximity is usually modeled in a continuous way. As of now, researchers working with the STERGM need to work with categorical definitions. Second, the robustness of the simulated networks, i.e. of the model converges, depends on a variety of factors that are hard to isolate (e.g., network size and continuous variables such as the amount of funding). This implies considerable difficulties in terms of finding the best-fitting model. Third, the discrepancy between methodological possibilities and data availability is the most apparent shortcoming of our study. Our study highlights and promotes the STERGM’s feature of disentangling link formation and dissolution processes. However, when looking at the most commonly used data for constructing spatial networks (such as that in the present paper), it turns out that most of the data encounter the same issues: either there is no (precise) available information on the duration of links (e.g., patent data, co-authorship data) or, if this information does exist, it might be subject to external conditions (e.g., relations established on the basis of the subsidization of joint R&D projects). Accordingly, while the methodological precision and possibilities to explore (spatial) network evolution continuously increase, the same cannot necessarily be said about the available data. Hence, researchers need to be aware of the gap existing regarding the methodological possibilities and what can actual been done with the data at hand. The opportunity to explore longitudinal two-mode network data with dynamic network analyses is hence a step in the right direction as it moves the methodological side closer to the type of data available. Nevertheless, we clearly pledge for more efforts to be directed toward the collection of data on link dissolution, as otherwise our understanding of knowledge network evolution will remain constrained.
Despite these shortcomings, some policy implications can be derived from the present study. Firstly, our results indicate that institutional proximity is still an important determinant of link formation. Given the wide belief in the necessity to involve heterogeneous sets of actors in R&D projects and that spillovers between the non-profit and profit sectors are to be increased (see, e.g., triple helix literature (Etzkowitz and Leydesdorff 2000)), these goals are not yet visible in our results. Profit organizations still seem to prefer to work with other profit organizations, and non-profit organizations are more frequently engaged with other non-profit organizations.
Secondly, as with other related studies, we found that proximities are important drivers of subsidized network formation. One can argue that these represent the “natural” way in which networks evolve without external influences. This is confirmed in many analyses on non-subsidized knowledge networks (Glückler 2010; Balland et al. 2013; Ter Wal 2014). Hence, networks influenced by a policy and those that are not influenced by such evolve in the same manner — i.e., they have the same factors driving their evolution. If this is the case, it may lead one to wonder why policy is providing subsidies for collaboration in the first place. When a policy supports the same kind of interactions that evolve independently of it, in the best of all cases, it merely increases the general magnitude of collaborations. However, it does not impact their structural composition. This particularly concerns cognitive proximity, which makes the establishment of projects generating significant novelty less likely (Boschma 2005; Nooteboom et al. 2007). In this respect, our study calls for a reconfiguration of the R&D subsidization policy.
Notes
This list of proximities is not exclusive. Other types of proximities may matter as well but have received considerably less attention in the literature so far.
In addition to the subsidies catalogue, the websites “Biotechnologie.de,” “chemie.de,” “Life-Sciences-Germany.com,” and “statista.de” and the homepages of the organizations have been used to acquire further data on organizational size and technological focus (cognitive proximity).
In general, the data allowed us to compute organizational proximity because of the distinction between beneficiary and executing entity. If two collaborating entities were departments of the same beneficiary, they would have a higher organizational proximity. However, in the data set at hand, this setting is extremely rare (around 1%) and, thus, very likely to be insignificant anyway.
Unfortunately, we could not assign a biotech subfield to every organization (see Table 6 in the appendix). Fortunately, the STERGM allows for excluding categories from the calculation, which we made use of when calculating the effect of cognitive proximity.
Bioinformatics was excluded as only 25 organizations are assigned to this category over the complete timespan.
As the categories of GEO PROX consist of approximately 80 regions, we excluded them as well, as it would have made the models too complex to calculate.
Our two-mode network has no triads and STERGM currently does not support the consideration of a two-mode clustering coefficient as, e.g., described by Opsahl (2013). We will therefore not further elaborate on triadic closure, which does not mean that it is of no relevance.
STERGM allows for calculating GWDEGREE for both levels (actor and event). A significantly negative coefficient will be obtained if the network shows a power law degree distribution. It means that at the actor mode, few organizations participate in many projects. At the event mode, few projects have many participants in this case.
Including GEO PROX in Models 1 and 3 led to degenerated results. Thus, we decided to exclude it. Nevertheless, degeneracy itself is an interesting topic and needs further research.
References
Anne LJ, Ter Wal, Ron A Boschma (2009) Applying social network analysis in economic geography: framing some key analytic issues. Ann Reg Sci 43 (3):739–756
Balland PA (2012) Proximity and the evolution of collaboration networks: evidence from research and development projects within the global navigation satellite system (GNSS) industry. Reg Stud 46:741–756
Balland PA, De Vaan M, Boschma R (2013) The dynamics of interfirm networks along the industry life cycle: the case of the global video game industry, 1987-2007. J Econ Geogr 13:741–765
Boschma R (2005) Proximity and innovation: a critical assessment. Reg Stud 39:61–74
Boschma R, Frenken K (2010) The spatial evolution of innovation networks: a proximity perspective. In: Boschma R, Martin R (eds) The handbook of evolutionary economic geography. Edward Elgar, Cheltenham, Cheltenham, pp 120–135
Boschma R, Martin R (2010) The aims and scope of evolutionary economic geography (No. 1001). Utrecht University, Section of Economic Geography
Boschma R, Ter Wal ALJ (2007) Knowledge networks and innovative performance in an industrial district: the case of a footwear district in the south of Italy. Ind Innov 14:177–199
Boschma R, Wenting R (2007) The spatial evolution of the British automobile industry: does location matter? Ind Corp Chang 16:213–238
Broekel T, Graf H (2012) Public research intensity and the structure of German R&D networks: a comparison of 10 technologies. Econ Innov New Technol 21:345–372
Broekel T, Hartog M (2013a) Explaining the Structure of Inter-Organizational Networks using Exponential Random Graph Model. Industry and Innovation 20:277–295
Broekel T, Hartog M (2013b) Determinants of Cross-Regional R&D Collaboration Networks: An Application of Exponential Random Graph Models. The Geography of Networks and R&D Collaborations. In: Scherngell T (ed) The geography of networks and R&D collaborations, advances in spatial science. Springer, Cham, pp 49–70
Broekel T, Balland PA, Burger M, van Oort F (2014) Modeling knowledge networks in economic geography: a discussion of four methods. Ann Reg Sci 53:423–452
Buchmann T, Pyka A (2015) The evolution of innovation networks: the case of a publicly funded German automotive network. Econ Innov New Technol 24:114–139
Bundesinstitut für Bau-, Stadt- und Raumforschung (BBSR) (2015) Laufende Raumbeobachtung – Raumabgrenzungen. Siedlungsstrukturelle Regionstypen http://www.bbsr.bund.de/BBSR/DE/Raumbeobachtung/Raumabgrenzungen/Regionstypen/regionstypen.html?nn=443270. Accessed 15 Jan 2016
Bundesministeriums für Bildung und Forschung (BMBF) (2008) Merkblatt für Antragsteller/Zuwendungsempfänger zur Zusammenarbeit der Partner von Verbundprojekten. Bundesministerium für Bildung und Forschung, BMBF Publik. Berlin: Federal Ministry of Education and Research. http://www.kooperation-international.de/fileadmin/public/Vordruck_0110.pdf. Accessed 30 Jan 2016
Cantner U, Meder A (2008) Regional and technological effects of cooperation behavior (no. 2008, 014). Jena economic research papers
Cohen WM, Levinthal DA (1990) Absorptive capacity: a new perspective on learning and innovation. Adm Sci Q 35:128–152
DaSilva E (2012) The colours of biotechnology: science, development and humankind. Electron J Biotechnol 7(3) http://www.ejbiotechnology.info/index.php/ejbiotechnology/article/view/1114/1496. Accessed 30 Jan 2016
Destatis (2016) Daten aus dem Gemeindeverzeichnis Kreisfreie Städte und Landkreise nach Fläche und Bevölkerung auf Grundlage des ZENSUS 2011 und Bevölkerungsdichte https://www.destatis.de/DE/ZahlenFakten/LaenderRegionen/Regionales/Gemeindeverzeichnis/Administrativ/Aktuell/04Kreise.html. Accessed 22 July 2017
Dohse D (2000) Technology policy and the regions - the case of the BioRegio contest. Res Policy 29:1111–1133
Ducruet C, Beauguitte L (2014) Spatial science and network science: review and outcomes of a complex relationship. Netw Spat Econ 14:297–316
Etzkowitz H, Leydesdorff L (2000) The dynamics of innovation: from National Systems and “mode 2” to a triple Helix of university–industry–government relations. Res Policy 29:109–123
Frank O, Strauss D (1986) Markov graphs. J Am Stat Assoc 81:832–842
Glückler J (2007) Economic geography and the evolution of networks. J Econ Geogr 7:619–634
Glückler J (2010) The evolution of a strategic alliance network: exploring the case of stock photography. In: Boschma R, Martin R (eds) The handbook of evolutionary economic geography. Edward Elgar, Cheltenham, pp 298–315
Glückler J, Doreian P (2016) Editorial: social network analysis and economic geography – positional, evolutionary and multi-level approaches. J Econ Geogr 16:1123–1134
Goodreau SM (2007) Advances in exponential random graph (p*) models applied to a large social network. Soc Networks 29:231–248
Hägerstrand T (1967) Innovation diffusion as a spatial process . The University of Chicago Press, Chicago
Hanneke S, Xing EP (2007) Discrete temporal models of social networks. In: Blei EADM, Goldenberg SEFA, Zheng E (eds) Statistical network analysis: models, issues, and new directions. Springer, Berlin, pp 115–125
Hanneke S, Fu W, Xing EP (2010) Discrete temporal models of social networks. Electron J Stat 4:585–605
Herrmann A, Taks J, Moors E (2012) Beyond regional clusters: on the importance of geographical proximity for R&D collaborations in a global economy — the case of the Flemish biotech sector. Ind Innov 19:499–516
Hoekman J, Scherngell T, Frenken K, Tijssen R (2013) Acquisition of European research funds and its effect on international scientific collaboration. J Econ Geogr 13:23–52
Hunter DR (2007) Curved exponential family models for social networks. Soc Networks 29:216–230
Hunter DR, Goodreau SM, Handcock MS (2008) Goodness of fit of social network models. J Am Stat Assoc 103:248–258
Illenberger J, Nagel K, Flötteröd G (2013) The role of spatial interaction in social networks. Networks and Spatial Economics 13:255–282
James S Coleman (1988) Social Capital in the Creation of Human Capital. Am J Sociol 94:S95–S120
Juyong Park, MEJ Newman (2004) Statistical mechanics of networks. Phys Rev E 70 (6)
Kreditanstalt für Wiederaufbau (KFW) (2012) KMU-Definition. Allgemeine Erläuterungen zur Definition der Kleinstunternehmen sowie der kleinen und mittleren Unternehmen (KMU) https://www.kfw.de/Download-Center/Förderprogramme-(Inlandsförderung)/PDF-Dokumente/6000000196-KMU-Definition.pdf. Accessed 30 Jan 2016
Krivitsky PN, Goodreau SM (2015) STERGM - Separable Temporal ERGMs for modeling discrete relational dynamics with statnet. https://cran.r-project.org/web/packages/tergm/vignettes/STERGM.pdf Accessed 30 Jan 2016
Krivitsky PN, Handcock MS (2014) A separable model for dynamic networks. J R Stat Soc Ser B (Stat Methodo) 76:29–46
Leifeld P, Cranmer SJ (2015) A theoretical and empirical comparison of the temporal exponential random graph model and the stochastic actor-oriented model. https://arxiv.org/pdf/1506.06696.pdf. Accessed 15 June 2018
Liu X, Derudder B, Liu Y, Witlox F, Shen W (2013) A stochastic actor-based modelling of the evolution of an intercity corporate network. Environ Plan A 45:947–966
Liu X, Derudder B, Liu Y (2015) Regional geographies of intercity corporate networks: the use of exponential random graph models to assess regional network-formation. Pap Reg Sci 94:109–126
Makino S, Chan CM, Isobe T, Baemish PW (2007) Intended and unintended termination of international joint ventures. Strateg Manag J 28:1113–1132
McPherson M, Smith-Lovin L, Cook JM (2001) Birds of a feather: homophily in social networks. Annu Rev Sociol 27:415–444
Meyer-Krahmer F (1985) Innovation behaviour and regional indigenous potential. Reg Stud 19:523–534
Morris M, Handcock MS, Hunter DR (2008) Specification of exponential-family random graph models: terms and computational aspects. J Stat Softw 24:1548
Murphy JT (2003) Social space and industrial development in East Africa: deconstructing the logics of industry networks in Mwanza. Tanzania J Econ Geogr 3:173–198
Nooteboom B, Van Haverbeke W, Duysters G, Gilsing V, van den Oord A (2007) Optimal cognitive distance and absorptive capacity. Res Policy 36:1016–1034
Opsahl T (2013) Triadic closure in two-mode networks: redefining the global and local clustering coefficients. Soc Networks 35:159–167
Paier MF, Scherngell T (2008) Determinants of Collaboration in European R&D Networks: Empirical Evidence from a Binary Choice Model Perspective. https://doi.org/10.2139/ssrn.1120081
Paier M, Scherngell T (2011) Determinants of collaboration in European R&D networks: empirical evidence from a discrete choice model. Ind Innov 18:89–104
Parkhe A (1991) Interfirm diversity, organizational learning, and longevity in global strategic alliances. J Int Bus Stud 22:579–601
Pierre-Alexandre Balland, David Rigby (2016) The geography of complex knowledge. Econ Geogr 93(1):1–23
Polidoro FJ, Ahuja G, Mitchell W (2011) When the social structure overshadows competitive incentives: the effects of network embeddedness on joint venture dissolution. Acad Manag J 54:203–223
Ponds R, Van Oort F, Frenken K (2007) The geographical and institutional proximity of research collaboration. Pap Reg Sci 86:423–443
Powell WW, Koput KW, Smith-Doerr L (1996) Interorganizational collaboration and the locus of innovation: networks of learning in biotechnology. Adm Sci Q 41:116–145
Robins G, Pattison P, Kalish Y, Lusher D (2007) An introduction to exponential random graph (p*) models for social networks. Soc Networks 29:173–191
Scherngell T, Barber MJ (2009) Spatial interaction modelling of cross-region R&D collaborations: empirical evidence from the 5th EU framework Programme. Pap Reg Sci 88:531–546
Scherngell T, Barber MJ (2011) Distinct spatial characteristics of industrial and public research collaborations: evidence from the fifth EU framework Programme. Ann Reg Sci 46:247–266
Ter Wal ALJ (2014) The dynamics of the inventor network in German biotechnology: geographic proximity versus triadic closure. J Econ Geogr 14:589–620
Tether BS (2002) Who co-operates for innovation, and why - an empirical analysis. Res Policy 31:947–967
Varas MLL (2007) Essays in social space: applications to Chilean communities on inter-sector social linkages, social capital, and social justice dissertation, University of Illinois, Urbana-Champaign
Vinciguerra S, Frenken K, Valente M (2010) The geography of internet infrastructure: an evolutionary simulation approach based on preferential attachment. Urban Stud 47:1969–1984
Wanzenböck I, Scherngell T, Lata R (2015) Embeddedness of European regions in European Union-funded research and development (R&D) networks: a spatial econometric perspective. Reg Stud 49:1685–1705
Zander U, Kogut B (1995) Knowledge and the speed of the transfer and imitation of organizational capabilities: an empirical test. Organ Sci 6:76–92
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Broekel, T., Bednarz, M. Disentangling link formation and dissolution in spatial networks: An Application of a Two-Mode STERGM to a Project-Based R&D Network in the German Biotechnology Industry. Netw Spat Econ 18, 677–704 (2018). https://doi.org/10.1007/s11067-018-9430-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11067-018-9430-1