Abstract
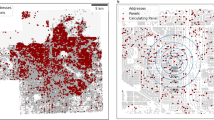
We test the existence of a neighborhood based peer effect around participation in an incentive based conservation program called ‘Water Smart Landscapes’ (WSL) in the city of Las Vegas, Nevada. We use 15 years of geo-coded daily records of WSL program applications and approvals compiled by the Southern Nevada Water Authority and Clark County Tax Assessors rolls for home characteristics. We use this data to test whether a spatially mediated peer effect can be observed in WSL participation likelihood at the household level. We show that epidemic spreading models provide more flexibility in modeling assumptions, and also provide one mechanism for addressing problems associated with correlated unobservables than hazards models which can also be applied to address the same questions. We build networks of neighborhood based peers for 16 randomly selected neighborhoods in Las Vegas and test for the existence of a peer based influence on WSL participation by using a Susceptible-Exposed-Infected-Recovered epidemic spreading model (SEIR), in which a home can become infected via autoinfection or through contagion from its infected neighbors. We show that this type of epidemic model can be directly recast to an additive-multiplicative hazard model, but not to purely multiplicative one. Using both inference and prediction approaches we find evidence of peer effects in several Las Vegas neighborhoods.






Similar content being viewed by others
Notes
In August 2000, the cap was 230 m2, which was increased to 5,800 m2 in Feb 2002, and further raised to 46,000 m2, while the median lot size is 650 m2 and the 99th percentile lot is 2,990 m2. Even the earliest cap, in August 2000 still allowed the full rebate to be afforded to 90% of conversion participants, and per household conversion size has generally fallen, rather than increased, as the program ages. Thus, is appears likely that these caps were primarily targeted at large commercial facilities such as golf courses.
Ownership rates are inferred by attributing to each home the block group level probability of a home being owner occupied vs renter occupied. This method is likely to underestimate the true difference.
Roughly 10% of homes in the WSL population had multiple approved conversions, removing some and then eventually all of the turf on the property. In this study, homes with multiple conversions are excluded.
Note that we are selecting preferred models on the basis of a better model fit, not a positive α value, but the model parameters that lead to a positive α value also fit the data better than models where the selected parameters result in α = 0.
References
Akaike H (1974) A new look at the statistical model identification. IEEE Trans Autom Control 19(6):716–723
Altarelli F, Braunstein A, Dall’Asta L, Lage-Castellanos A, Zecchina R (2014a) Bayesian inference of epidemics on networks via belief propagation. Phys Rev Lett 112(11):118701
Altarelli F, Braunstein A, Dall’Asta L, Wakeling JR, Zecchina R (2014b) Containing epidemic outbreaks by message-passing techniques. Phys Rev X 4(2):021024
Anderson RM, May RM, Anderson B (1992) Infectious diseases of humans: dynamics and control, vol 28. Wiley Online Library
Angrist JD (2014) The perils of peer effects. Labour Econ 30:98–108
Aral S, Walker D (2012) Identifying influential and susceptible members of social networks. Science 337(6092):337–341
Aral S, Muchnik L, Sundararajan A (2009) Distinguishing influence-based contagion from homophily-driven diffusion in dynamic networks. Proc Natl Acad Sci 106(51):21544–21549
Baranzini A, Carattini S, Péclat M (2017) What drives social contagion in the adoption of solar photovoltaic technology? Center for Climate Change Economics and Policy Working Paper No. 308
Barthélemy M, Flammini A (2009) Co-evolution of density and topology in a simple model of city formation. Netw Spatial Econ 9(3):401–425
Bollinger B, Gillingham K (2012) Peer effects in the diffusion of solar photovoltaic panels. Market Sci 31(6):900–912
Brelsford C (2014) Whiskey is for drinking; water is for fighting over: population growth, infrastructure change, and conservation policy as drivers of residential water demand. Arizona State University
Brelsford C, Abbott JK (2017) Growing into water conservation? Decomposing the drivers of reduced water consumption in Las Vegas, NV. Ecol Econ 133:99–110
Brelsford C, Abbott JK (2018) How smart are ‘Water Smart Landscapes’? arXiv:1803.04593
Brock WA, Durlauf SN (2001) Interactions-based models. Handb Econ 5:3297–3380
Byrd RH, Lu P, Nocedal J, Zhu C (1995) A limited memory algorithm for bound constrained optimization. SIAM J Sci Comput 16(5):1190–1208
Ducruet C, Beauguitte L (2014) Spatial science and network science: Review and outcomes of a complex relationship. Netw Spatial Econ 14(3–4):297–316
Federal Reserve Bank of St. Louis (2018) New private housing units authorized by building permits: 1-Unit structures for Las Vegas-Paradise, NV (MSA) [lasv832bp1fhsa]. Technical Report [LASV832BP1FHSA], FRED, Federal Reserve Bank of St. Louis
Graziano M, Gillingham K (2015) Spatial patterns of solar photovoltaic system adoption: the influence of neighbors and the built environment. J Econ Geogr 15 (4):815–839
Hogan J (2016) Strip left reeling: picking up the pieces after the Great Recession. Las Vegas Review-J
Höhle M (2008) Spatio-temporal epidemic modelling using additive-multiplicative intensity models. University of Munich, Department of Statistics, Technical Report Number 041 https://epub.ub.uni-muenchen.de/6366/2/hoehle-techrep41.pdf
Höhle M (2009) Additive-multiplicative regression models for spatio-temporal epidemics. Biom J 51(6):961–978
Höhle M, Jørgensen E, O’Neill PD (2005) Inference in disease transmission experiments by using stochastic epidemic models. J R Stat Soc Ser C Appl Stat 54 (2):349–366
Iyengar R, Van den Bulte C, Valente TW (2011) Opinion leadership and social contagion in new product diffusion. Mark Sci 30(2):195–212
Kalbfleisch JD, Prentice RL (2011) The statistical analysis of failure time data, vol 360. Wiley, New York
Kermack WO, McKendrick AG (1932) Contributions to the mathematical theory of epidemics. ii. the problem of endemicity. Proc R Soc London, Ser A, containing papers of a mathematical and physical character 138(834):55–83
Manski CF (1993) Identification of endogenous social effects: the reflection problem. Rev Econ Stud 60(3):531–542
Manski CF (2000) Economic analysis of social interactions. J Econ Perspect 14(3):115–136
Meyer S, Held L, Höhle M (2017) Spatio-temporal analysis of epidemic phenomena using the R package surveillance. J Stat Softw, Articles 77(11):1–55
Pawitan Y (2001) In all likelihood: statistical modelling and inference using likelihood. Oxford University Press, Oxford
Richter L-L (2013) Social effects in the diffusion of solar photovoltaic technology in the UK. Cambridge Working Papers in Economics 1357, https://doi.org/10.17863/CAM.5680
Ryan C (2017) Measurement of Peer Effects. Aust Econ Rev 50(1):121–129
Scheike TH, Zhang M-J (2002) An additive–multiplicative cox–aalen regression model. Scand J Stat 29(1):75–88
Segall E (2017) Number of vacant homes in Las Vegas rises. Las Vegas Rev-J
Shalizi CR, Thomas AC (2011) Homophily and contagion are generically confounded in observational social network studies. Sociol Methods Res 40(2):211–239
Shao J (1993) Linear model selection by cross-validation. J Am Stat Assoc 88 (422):486–494
Soetevent AR (2006) Empirics of the identification of social interactions; an evaluation of the approaches and their results. J Econ Surv 20(2):193–228
Southern Nevada Water Authority (2018) Frequent questions - water smart landscapes. www.snwa.com/rebates/wsl_faq.html. Accessed 3 Jan 2018
Sovocool KA, Morgan M, Bennett D (2006) An in-depth investigation of xeriscape as a water conservation measure. J Am Water Works Assoc 98(2):82–93
Towe C, Lawley C (2013) The contagion effect of neighboring foreclosures. Am Econ J Econ Pol 5(2):313–335
U.S. Bureau of Economic Analysis (2018) Total gross domestic product for Las Vegas-Henderson-Paradise, NV (MSA) [NGMP29820]. Technical Report [NGMP29820], FRED, Federal Reserve Bank of St. Louis
U.S. Bureau of Labor Statistics (2018) Unemployment rate in Las Vegas-Henderson-Paradise, NV (MSA) [lasv832urn]. FRED Federal Reserve Bank of St. Louis, Federal Reserve Bank, St. Louis
U.S. Federal Housing Finance Agency (2018) All-transactions house price index for Las Vegas-Henderson-Paradise, NV (MSA) [ATNHPIUS29820q]. Technical Report [ATNHPIUS29820Q], FRED, Federal Reserve Bank of St. Louis
Vallès-Català T, Peixoto TP, Guimerà R, Sales-Pardo M (2017) On the consistency between model selection and link prediction in networks. arXiv:1705.07967
Young HP (2009) Innovation diffusion in heterogeneous populations: Contagion, social influence, and social learning. Am Econ Rev 99(5):1899–1924
Acknowledgements
We thank Alfredo Braunstein and Joshua K Abbott for helpful comments. Research sponsored by the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory, managed by UT-Battelle, LLC, for the US Department of Energy. CB also received partial support from the ASU/SFI Center for Biosocial Complexity. CDB was supported by the John Templeton Foundation.
Author information
Authors and Affiliations
Corresponding author
Additional information
This manuscript has been co-authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).
Appendices
Appendix A
1.1 A.1 Log Likelihood of the Epidemic Model
1.2 A.2 Mapping Epidemic with Autoinfection to Additive-Multiplicative Hazard Model
Here we outline how the three models SI, additive-multiplicative and multiplicative hazard, describe the same quantity of interest, the hazard rate λ(ti|Θ, D). In discrete time, this is the conditional probability that an event happens at time ti, given it has not yet happened before. In general this quantity can depend on a set of parameters Θ and the data D. In our case Θ = {α, μ} include the transmission and autoinfection probabilities of all nodes, whereas D = {tiE}, i.e. the data are the observed exposure times. In the SEIR model, (1 minus) the hazard rate of a susceptible node i at time t is:
In discrete time (Kalbfleisch and Prentice 2011), the hazard rate in the additive-multiplicative hazard model (Höhle et al. 2005; Höhle 2008) can be written as:
whereas, in the purely multiplicative model used in Towe and Lawley (2013) we have:
where \({\lambda _{0}^{t}}\) is the baseline hazard at time t which represents a global contribution to the probability of getting infected which is the same for all houses; \(\bar {x}_{i}\) is a vector of covariates and \(\bar {\beta }\) is a vector of parameters coupling the covariates, in a similar flavor as in linear regression.
Comparing Eqs. 8 and 9 we obtain the mapping (4).
1.2.1 Proof
From the definition of hazard rate (Kalbfleisch and Prentice 2011) which, in discrete time, is a conditional probability, we have a relationship connecting the probability f(ti) of an event happening at time ti and the survival probability S(ti), which is the probability that no event happens before time ti (but it can happen at exactly ti or later):
Notice that for discrete time \(S(t)={\sum }_{s=t}^{\infty } f(s)\), thus we can write:
Substituting into Eq. 11:
Using the equation valid in general (Kalbfleisch and Prentice 2011) relating the survival probability S(t) with the hazard rate \(S_{i}(t)=e^{-{{\int }_{0}^{t}} \lambda _{i}(s) ds}\), the following relation valid for additive-multiplicative hazard model as in Scheike and Zhang (2002), where \({\lambda _{i}^{t}}=\alpha {n_{i}^{t}}+\lambda _{0} e^{\bar {x_{i}} \cdot \bar {\beta }}\) with covariates can be derived:
where S0(t) represents the baseline survival probability when \(\bar {\beta }= 0\) and no epidemic effect is present (α = 0), whereas \(S^{i}_{epi}(t)\) represents the epidemic contribution to the survival probability.
For discrete models we can write:
Substituting Eqs. 16 and 17 into Eq. 14, we get:
For the purely Multiplicative hazard model as in Towe and Lawley (2013) where \({\lambda _{i}^{t}}={\lambda _{0}^{t}} e^{\bar {x_{i}} \cdot \bar {\beta }} e^{\alpha {n_{i}^{t}}}\) we cannot separate the baseline and epidemic contribution as above, instead we have:
which leads to:
Appendix B: Estimate of WSL Rates’ Increase Due to the Presence of Active Neighbors
Here we estimate the increased number of participating houses due to the presence of active neighbors compared to what we would have observed in a counter-factual scenario where houses do not have any participating neighbors, in the model that allows for peer effects. In this way, the model is kept as faithful as possible to our best estimate models, but we prevent peer effects from occurring. The difference in WSL activation rates can then be attributed to peer effects, as described by our model.
In general, estimating this quantity analytically is not possible because the evolution of the activation dynamics depends on the entire history of the process, i.e. the dynamics are non Markovian; for instance, having 10 active neighbors at time T (and recovery τR > 10) and all of whom activated at T − 1 is different than having 10 active neighbors at time T but with one of them activating at T − 10, one at T − 9 and so on up to T − 1. In the former case the probability of activating will be a function of (1 − α)10, whereas in the latter it will be a function of (1 − α)(1 − α)2…(1 − α)10. In addition, the autoinfection probability varies from house to house based on covariates, and the epidemic term also varies from house to house based on the local network topology: the number of neighbors.
Therefore we run Markov Chain Monte Carlo simulations using the epidemic model with the parameters inferred in the prediction results of Table 5 but forcing the transmission probability α = 0. This is equivalent to the scenario where a house does not have any active neighbors, so that the final number of active houses obtained at the end of the 36-month period with this procedure will be a lower bound of the one we would get if each house were to have, at each time step in the observation period, a variable number of active neighbors \(0 \leq {n_{i}^{t}} \leq k_{i}\), where ki is the number of neighbors of node i (also known as the degree of a node in the network). We then calculate \(r_{peer}=(\hat {I}^{Sim}_{T}-\hat {I}^{Sim}_{T,\alpha = 0})/{\Delta } \hat {I}_{\alpha = 0}\), the ratio between the increase in WSL rate at the end of the observation period between the case where houses have active neighbors, \(\hat {I}^{Sim}_{T}\) (as in Table 5), and when we force α = 0, \(\hat {I}^{Sim}_{T,\alpha = 0}\), over the increase in WSL rate during the last 36 months when houses do not have any participating neighbor \({\Delta } \hat {I}_{\alpha = 0}=\hat {I}^{Sim}_{T,\alpha = 0}-{I}^{obs}_{T-36,\alpha = 0}\), where \({I}^{obs}_{T-36,\alpha = 0}\) is the observed WSL rate at the beginning of the last 36-month period. We then consider the observed increase in number of participating houses during the last 36 months of the observation period ΔNobs and calculate ΔNpeer = rpeerΔNobs as an estimate of the number of participating houses in the 36 months due to peer effect. In Table 7 we show the results: the impact of peer effect varies across neighborhoods, from small impact as in neighborhood 11 of a 3% to a 27% increase of neighborhood 7.
Rights and permissions
About this article
Cite this article
Brelsford, C., De Bacco, C. Are ‘Water Smart Landscapes’ Contagious? An Epidemic Approach on Networks to Study Peer Effects. Netw Spat Econ 18, 577–613 (2018). https://doi.org/10.1007/s11067-018-9416-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11067-018-9416-z