Supply Chain Network Designs Developed for Deteriorating Items Under Conditions of Trade Credit and Partial Backordering

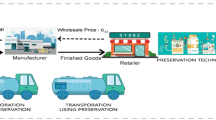
Abstract

Deteriorating items, trade credit, and partial backordering are common in today’s business. However, no previous study on supply chain network design has considered these business aspects together. In this paper, we present supply chain networks designed for deteriorating items under trade credit and two conditions: (a) no shortage and (b) partial backordering of goods. We also present 2 algorithms based on nonlinear optimization that were developed in order to optimize the influence area and the joint replenishment-cycle time in the no-shortage case, and to identify the optimal shortage level in the partial-backordering case. The numerical examples presented herein illustrate how the solution procedure works. The effects of various values of the tested parameters on decisions and costs are also discussed. Our results could be used as a reference by managers when making business decisions.

Appendix

For total network cost function to be convex, the following sufficient conditions should be contented:

$$ H=\left|\begin{array}{cc}\hfill \frac{\partial^2TC\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {s}^2}\hfill & \hfill \frac{\partial^2TC\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial s\partial {A}_i}\hfill \\ {}\hfill \frac{\partial^2TC\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial s\partial {A}_i}\hfill & \hfill \frac{\partial^2TC\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {A_i}^2}\hfill \end{array}\right|>o\kern0.5em \mathrm{and}\kern0.5em \frac{\partial^2TC\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {s}^2}>0. $$

By taking the second derivative of Eq. (1) with respect to A _i , s, we get

$$ \frac{\partial^2T{C}_1\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {s}^2}={\displaystyle \sum_{i=1}^N}\frac{hT\zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i}+{\displaystyle \sum_{i=1}^N}\frac{bT\beta \zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i}+{\displaystyle \sum_{i=1}^N}\frac{cT\zeta \theta {c}_i^2{\delta}_i{\lambda}_i}{A_i}+{\displaystyle \sum_{i=1}^N}\frac{cT\zeta {i}_p{c}_i^2{\delta}_i{\lambda}_i}{A_i}+{\displaystyle \sum_{i=1}^N}\frac{c{T}^2\beta \zeta {C}_i^2{\delta}_i{\lambda}_i}{A_i}, $$

(A1)

$$ \begin{array}{l}\frac{\partial^2T{C}_1\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {A_i}^2}=\left|\begin{array}{l}{\displaystyle \sum_{i=1}^N}\frac{2F{c}_i}{A_i^3}+{\displaystyle \sum_{i=1}^N}\frac{2O{c}_i}{T{A}_i^3}+{\displaystyle \sum_{i=1}^N}\frac{h{\left(1-s\right)}^2T\zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^3}+{\displaystyle \sum_{i=1}^N}\frac{2gs\left(1-\beta \right)\zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^3}+{\displaystyle \sum_{i=1}^N}\frac{b{s}^2T\beta \zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^3}\\ {}+{\displaystyle \sum_{i=1}^N}\frac{c{\left(1-s\right)}^2T\zeta \theta {c}_i^2{\delta}_i{\lambda}_i}{A_i^3}+{\displaystyle \sum_{i=1}^N}\frac{2c\zeta \left(1-s+\frac{1}{2}\left(1-s\right)T\theta \right){c}_i{C}_i{\delta}_i{\lambda}_i}{A_i^3}+{\displaystyle \sum_{i=1}^N}\frac{c{s}^2{T}^2\beta \zeta {C}_i^2{\delta}_i{\lambda}_i}{A_i^3}\\ {}+{\displaystyle \sum_{i=1}^N}-\frac{\zeta {c}_i{c}_r{f}_r{\delta}_i{\lambda}_i}{4{A}_i^{3/2}}+{\displaystyle \sum_{i=1}^N}\frac{c\zeta {\mathrm{i}}_p{c}_i^2{\left(\left(1-s\right)T-{t}_c\right)}^2{\delta}_i{\lambda}_i}{T{A}_i^3}-{\displaystyle \sum_{i=1}^N}\frac{w\zeta {\mathrm{i}}_e{c}_i^2{t}_c^2{\delta}_i{\lambda}_i}{T{A}_i^3}\end{array}\right|,\\ {}\end{array} $$

(A2)

$$ \begin{array}{l}\frac{\partial^2T{C}_1\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial s\partial {A}_i}=\left|\begin{array}{l}{\displaystyle \sum_{i=1}^N}\frac{h\left(1-s\right)T\zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^2}+{\displaystyle \sum_{i=1}^N}-\frac{g\left(1-\beta \right)\zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^2}+{\displaystyle \sum_{i=1}^N}-\frac{bsT\beta \zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^2}+{\displaystyle \sum_{i=1}^N}\frac{c\left(1-s\right)T\zeta \theta {c}_i^2{\delta}_i{\lambda}_i}{A_i^2}\\ {}-{\displaystyle \sum_{i=1}^N}-\frac{Tw\zeta {\mathrm{i}}_e{c}_i^2{\delta}_i{\lambda}_i}{2{A}_i^2}+{\displaystyle \sum_{i=1}^N}-\frac{c\zeta \left(-1-\frac{T\theta }{2}\right){c}_i{C}_i{\delta}_i{\lambda}_i}{A_i^2}+{\displaystyle \sum_{i=1}^N}-\frac{cs{T}^2\beta \zeta {C}_i^2{\delta}_i{\lambda}_i}{A_i^2}\end{array}\right|.\\ {}\end{array} $$

(A3)

With the stable point (A ^* _i1 , s ^*₁ ), we check for convexity. The sufficient optimal conditions for minimizing TC ₁(A ₁, A ₂ … A _n , T, s) are

$$ \frac{\partial^2T{C}_1\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {s}^2}>0\ \forall\ {A}_1,{A}_2\dots {A}_n,T,s $$

(A4)

$$ \begin{array}{l}H=\left(\frac{\partial^2T{C}_1\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {s}^2}\right)*\left(\frac{\partial^2T{C}_1\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {A_i}^2}\right)-{\left(\frac{\partial^2T{C}_1\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {A}_i\partial s}\right)}^2\\ {}=\left|\begin{array}{l}{\displaystyle \sum_{i=1}^N}\frac{\zeta {\lambda}_i{\delta}_i{C}_i^3}{4{A}_i^4}\left(4\zeta {\lambda}_i{\delta}_i{C}_i\left({g}^2{\left(1-\beta \right)}^2+2gT\left(1-\beta \right)\left(h+c\theta \right)+b{T}^2\beta \left(h+c\theta \right)-w\left(h+b\beta +c\theta \right){I}_e{t}_c^2\right.\right)\\ {}+{\displaystyle \sum_{i=1}^N}\frac{\zeta {\lambda}_i{\delta}_i{C}_i^3}{4{A}_i^4}\left(h+b\beta +c\theta \right)\left(8\left(O+FT\right)-T{A}_i^{\frac{3}{2}}{C}_r{f}_r\zeta {\lambda}_i{\delta}_i\right)+{\displaystyle \sum_{i=1}^N}\frac{\zeta {\lambda}_i{\delta}_i{C}_i^3}{4{A}_i^4}\left(c\left(-1+s\right)T\zeta \left(2+T\theta \right){C}_i{\delta}_i{\lambda}_i\right)\\ {}+{\displaystyle \sum_{i=1}^N}\frac{\zeta {\lambda}_i{\delta}_i{C}_i^3}{4{A}_i^4}\left(c{I}_p\left(8O+8FT-T{A}_i^{\frac{3}{2}}{C}_r{f}_r\zeta {\lambda}_i{\delta}_i+4\zeta {\lambda}_i{\delta}_i{C}_i\left(T\left(2g\left(1-\beta \right)+b\beta T\right)+\left(h+b\beta +c\theta +w{I}_e\right){t}_c^2\right)\right)\right)\end{array}\right|\\ {}\end{array} $$

$$ \mathrm{And}\kern0.5em H>0\ \forall\ {A}_1,{A}_2\dots {A}_n,\mathrm{T},\mathrm{s}\kern0.5em . $$

(A5)

Thus, we know that inequalities equations (A4) and (A5) satisfy the sufficient condition. Now, we prove that TC ₂(A ₁, A ₂ … A _n , T, s) is a convex function in A _i , s.

Likewise, by taking the second derivative of Eq. (2) with respect to both of selling price, we get

$$ \frac{\partial^2T{C}_2\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {s}^2}={\displaystyle \sum_{i=1}^N}\frac{hT\zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i}+{\displaystyle \sum_{i=1}^N}\frac{bT\beta \zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i}+{\displaystyle \sum_{i=1}^N}\frac{cT\zeta \theta {c}_i^2{\delta}_i{\lambda}_i}{A_i}+{\displaystyle \sum_{i=1}^N}\frac{c{T}^2\beta \zeta {C}_i^2{\delta}_i{\lambda}_i}{A_i} $$

(A6)

$$ \begin{array}{l}\frac{\partial^2T{C}_2\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {A_i}^2}=\left|\begin{array}{l}{\displaystyle \sum_{i=1}^N}\frac{2F{c}_i}{A_i^3}+{\displaystyle \sum_{i=1}^N}\frac{2O{c}_i}{T{A}_i^3}+{\displaystyle \sum_{i=1}^N}\frac{h{\left(1-s\right)}^2T\zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^3}+{\displaystyle \sum_{i=1}^N}\frac{2gs\left(1-\beta \right)\zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^3}\\ {}+{\displaystyle \sum_{i=1}^N}\frac{b{s}^2T\beta \zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^3}+{\displaystyle \sum_{i=1}^N}\frac{c{\left(1-s\right)}^2T\zeta \theta {c}_i^2{\delta}_i{\lambda}_i}{A_i^3}+{\displaystyle \sum_{i=1}^N}\frac{2c\zeta \left(1-s+\frac{1}{2}\left(1-s\right)T\theta \right){c}_i{C}_i{\delta}_i{\lambda}_i}{A_i^3}\\ {}+{\displaystyle \sum_{i=1}^N}\frac{c{s}^2{T}^2\beta \zeta {C}_i^2{\delta}_i{\lambda}_i}{A_i^3}+{\displaystyle \sum_{i=1}^N}-\frac{\zeta {c}_i{c}_r{f}_r{\delta}_i{\lambda}_i}{4{A}_i^{3/2}}-{\displaystyle \sum_{i=1}^N}\frac{2w\zeta {i}_e{c}_i^2\left(-\frac{1}{2}\left(1-s\right)T+{t}_c\right){\delta}_i{\lambda}_i}{A_i^3}\end{array}\right|\\ {}\end{array} $$

(A7)

$$ \frac{\partial^2T{C}_2\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial s\partial {A}_i}=\left|\begin{array}{l}{\displaystyle \sum_{i=1}^N}\frac{h\left(1-s\right)T\zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^2}+{\displaystyle \sum_{i=1}^N}-\frac{g\left(1-\beta \right)\zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^2}+{\displaystyle \sum_{i=1}^N}-\frac{bsT\beta \zeta {c}_i^2{\delta}_i{\lambda}_i}{A_i^2}\\ {}+{\displaystyle \sum_{i=1}^N}\frac{c\left(1-s\right)T\zeta \theta {c}_i^2{\delta}_i{\lambda}_i}{A_i^2}-{\displaystyle \sum_{i=1}^N}-\frac{Tw\zeta {\mathrm{i}}_e{c}_i^2{\delta}_i{\lambda}_i}{2{A}_i^2}+{\displaystyle \sum_{i=1}^N}-\frac{c\zeta \left(-1-\frac{T\theta }{2}\right){c}_i{C}_i{\delta}_i{\lambda}_i}{A_i^2}\\ {}+{\displaystyle \sum_{i=1}^N}-\frac{cs{T}^2\beta \zeta {C}_i^2{\delta}_i{\lambda}_i}{A_i^2}\end{array}\right|. $$

(A8)

We can see that

$$ \frac{\partial^2T{C}_2\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {s}^2}>0\ \forall\ {A}_1,{A}_2\dots {A}_n,T,s $$

(A9)

$$ \begin{array}{l}H=\left(\frac{\partial^2T{C}_2\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {s}^2}\right)*\left(\frac{\partial^2T{C}_2\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {A_i}^2}\right)-{\left(\frac{\partial^2T{C}_2\left({A}_1,{A}_2\dots {A}_n,T,s\right)}{\partial {A}_i\partial s}\right)}^2\\ {}\kern1.5em =\left|\begin{array}{l}{\displaystyle \sum_{i=1}^N}\frac{\zeta {\lambda}_i{\delta}_i{C}_i^3}{4{A}_i^4}{\left(4\zeta {\lambda}_i{\delta}_i{C}_i\left(g\left(1-\beta \right)+T\right.\left(h-hs-bs\beta +c\theta -cs\theta \right)+T{w}_e\right)}^2\\ {}+{\displaystyle \sum_{i=1}^N}\frac{\zeta {\lambda}_i{\delta}_i{C}_i^3}{4{A}_i^4}\left(h+b\beta +c\theta \right)\left(8O+8FT-T{A}_i^{\frac{3}{2}}{C}_r{f}_r\zeta {\lambda}_i{\delta}_i\right)+{\displaystyle \sum_{i=1}^N}\frac{\zeta {\lambda}_i{\delta}_i{C}_i^3}{4{A}_i^4}\left(cT\zeta \left(2+T\theta \right){C}_i{\delta}_i{\lambda}_i\right)\\ {}+{\displaystyle \sum_{i=1}^N}\frac{\zeta {\lambda}_i{\delta}_i{C}_i^3}{4{A}_i^4}\left(h+b\beta +c\theta \right)\left(4\zeta {\lambda}_i{\delta}_i{C}_i\left(T\left(2g\left(1-\beta \right)+Y\left(h{\left(-1+s\right)}^2\theta \right.\right)+\left(\left.T-sT+2{t}_c\right)w{I}_e\right){t}_c^2\right)\right)\end{array}\right|\end{array} $$

$$ \mathrm{And}\ H>0\ \forall\ {A}_1,{A}_2\dots {A}_n,\mathrm{T},\mathrm{s}\;. $$

(A10)

Then, we find that inequalities (A9) and (A10) satisfy the following sufficient conditions. The total network function TC(A ₁, A ₂ … A _n , T, s) is also a convex function in A _i , s.