Special Issue on Transport Infrastructure: A Route Choice Experiment with an Efficient Toll

Abstract

Traffic congestion is a substantial time cost for many urban commuters. This paper studies the response of subjects in an experimental setting in which subjects choose between a short direct route that becomes increasingly congested as more people travel on it and a more indirect route that does not become congested. More specifically, I investigate how subjects respond to the use of a toll that theory predicts will minimize travel time costs. The experimental results reported in this paper show that this toll comes very close to achieving efficient use of the travel network.

In real traffic environments, coordination problems occur in any congested area on a daily basis. Thousands of drivers try to determine the “best” route to travel on, based on the information they have about traffic speed on their set of route choices on previous days and/or current traffic reports. In such a situation, thousands of drivers essentially make simultaneous travel decisions without the ability to coordinate, which leads to equilibrium being an unlikely occurrence on many congested routes. Furthermore, cooperation that could lead to more efficient outcomes is not seen much (if at all) on congested routes.

This situation is similar to coordination games, as discussed in Ochs (1995). Cooper et al. (1990) describe coordination games as “a class of symmetric, simultaneous move, complete information games” (p. 218). In these games, multiple Nash equilibria exist. However, there may also exist outcomes that are better for all participants but are not Nash equilibria.

One specific type of coordination game involves a congested transportation network, which could have inelastic or elastic trip demand (e.g. de Palma 1992). In this type of game, each person receives a benefit if the trip is made, but typically incurs two types of costs. The first cost is due to the time required to travel a particular distance under congestion-free conditions. This cost is dependent on the route chosen. The second type involves costs due to congestion. These costs are dependent on the route chosen and the number of other people deciding to travel the same route.

In one type of transportation network, drivers must travel on one of two routes, one congested and one uncongested. The congested route is the shorter of the two in distance, but this entices at least some of the drivers to this route. This leads to the Pigou-Knight-Downs paradox. As long as at least one driver is on the uncongested route, all subjects have the same travel time, equal to the time on the uncongested route.¹ This is also known as a user equilibrium by Wardrop’s (1952) first principle. However, if the drivers coordinated their efforts, or a central planner could enforce the Vickrey-Clarke-Groves mechanism,² they could decide to have fewer drivers than the equilibrium number on the congested route. This would result in a faster travel time on the congested route. The system optimal point, which comes from Wardrop’s second principle, is the point that minimizes the total costs of driving. For example, in a world of drivers with homogeneous values of time, an optimal outcome could have a different group traveling the congested route each day so that each driver could travel the congested route some of the time, resulting in an outcome that Pareto-dominates any Nash equilibrium. Although all drivers are better off if they all follow the agreement, this outcome is not a Nash equilibrium if they are not bound to follow it. More specifically, it is not a Nash equilibrium because any single driver could deviate and travel the congested route on a day that he is assigned to the uncongested route, leading to a better travel time for that driver. This paper uses a different mechanism than the one described above, with a toll used to discourage travel on the congested route.

1 Congestion experiments

In recent years, experiments have been used to explore human behavior on various traffic networks. These experiments pay subjects based on their performance in the experiment, with better performance resulting in higher payouts. The experiments listed below use modifications of the Pigou-Knight-Downs paradox. Before discussing the findings of these experiments, it is important to emphasize that only one of these experiments uses tolls as a mechanism for improving average travel time. A brief summary of the congestion experiments described below, along with a few others, is found in Table 1. Note that all of these experiments have subject profiles that are the same for each person, and that total demand is typically inelastic for traveling through the route network described.

Table 1 A summary of select congestion experiments

Selten et al. (2007) modify the two-route network described by the Pigou-Knight-Downs paradox by allowing both routes to be congestible. In this experiment, 18 subjects must travel between two points on either a “main” road or a “side” road, where the side road requires more travel time than the main road if the number of subjects traveling on both routes is the same. Subjects then receive a payout in each round as a function of travel time, with higher travel time resulting in a lower payout. These choices are repeated over 200 rounds, with theory predicting a user equilibrium of 12 subjects on the main route. On average, subject route choices come very close to the theoretical predictions. However, since the population in this experiment is homogeneous and no tolls are charged, any subject’s route choice can be part of an equilibrium as long as 12 subjects travel the main route, since theory only predicts the number of people on each route. With thousands of equilibria possible, any subject could be on either route in equilibrium, leading to substantial fluctuations of the number of travelers on each route from round to round, even in rounds after equilibrium. Although such fluctuations reject the predictions of pure-strategy equilibrium, the mean number of travelers on each route comes close to this equilibrium.

Chmura and Pitz (2004a, b) modify the payoffs by using a minority game structure.³ Although the minority game framework is useful in many economic settings, it may not be the best way to model the payoffs in a transportation network because commuters typically do not “win” or “lose,” but rather incur one of many possible commuting costs.

Two results from the Selten et al. (2007) and Chmura and Pitz (2004a, b) experiments are worth highlighting. First, a person’s payout in one round is negatively correlated to the likelihood that the same person will switch routes in the following round. This implies that many subjects think that the “other” route will be the better choice after a relatively bad payout. In other words, many people believe that a relatively bad payout follows another relatively bad payout if they remain on the same route from one round to the next. Second, subjects who switch routes frequently over the course of the experiment tend to have worse overall payouts than those who switch less frequently. These results shed some light on how subjects react when faced with a coordination problem, and how their reactions affect overall payoffs.

2 A two-route model with only one route that congests

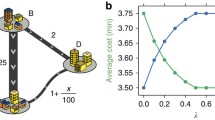
Suppose a group of people need to travel from point A to point B, and that each person has the option to travel on an uncongested but indirect highway, or a more direct but narrow bridge that gets congested (See Fig. 1).⁴ In other words, highway travel time is independent of the number of travelers, while travel time on the bridge is an increasing function of bridge traffic. Assume that the per-minute travel time cost is independent of route choice. This rules out the possibility that the more scenic route is preferred, all else being equal. Given this framework, it is easy to show that under the standard assumption of homogeneous travel time costs (using uniform point deductions in an experimental setting) equilibrium occurs when the total cost to commuters (including tolls, if any) is identical on both routes.⁵

Fig. 1

A visual of the scenario that subjects see for their travel situation

2.1 The no-toll case equilibrium

In the absence of tolls, the only costs of traveling from point A to point B are time costs. In this example, I assume that each person’s per-minute travel time costs are homogeneous. For simplicity, I assume that N commuters know the travel time on the bridge (t _B ) and the highway (t _H ) with certainty. (See Table 2 for a description of all variables and constants used in this paper.) In particular, they know that travel time on the highway is constant and that travel time on the bridge is an increasing linear function of the number of travelers on the bridge (Q) with intercept α and slope β, such that:

$$ {t_B} = \alpha + \beta Q. $$

(1)

Table 2 Variable/constant table

For each additional traveler on the bridge, time increases by β minutes. Based on the above information, drivers can determine the marginal private benefit (MPB) of traveling the bridge relative to the highway. If Q drivers travel the bridge, the MPB in minutes of the Qth person traveling the bridge is the difference in travel time between the two routes, or ${t_H} - \left( {\alpha + \beta Q} \right)$. To convert the travel time into monetary terms, the time saved needs to be multiplied by the individual’s value of time:

$$ MP{B_Q} = \left( {{t_H} - \left( {\alpha {\text{ }} + {\text{ }}\beta Q} \right)} \right) \times V, $$

(2)

where V represents the value of time for the Qth person to travel the bridge. Based on the following assumptions, MPB is a decreasing linear function,⁶ as shown in Fig. 2: (1) V is constant for each traveler; (2) each traveler’s value of V is the same in a homogeneous framework; (3) the marginal opportunity cost of travel time is assumed to be independent of trip length; and (4) time savings decrease linearly with Q.

Fig. 2

Marginal external cost (MEC) and marginal private benefit (MPB) in a homogeneous value of time case

I also assume that subjects maximize utility by minimizing travel time. Equilibrium therefore occurs when the travel time on both routes is the same, or at the point where MPB is zero:⁷

$$ {t_B} = {t_H} \Rightarrow \hat Q = \frac{{{t_H} - \alpha }}{\beta }. $$

(3)

Finally, although theory is able to predict the number of people on each route in equilibrium, it is unable to predict the route that any particular person travels. Since any person can travel on either route in equilibrium, any combination of $\hat Q$ people on the bridge constitutes an equilibrium. Thus, there exist $\left( {\begin{array}{*{20}{c}} N \\ {\hat Q} \\ \end{array} } \right)$ equilibrium combinations.

2.2 Tolls and efficiency in a homogeneous time cost setting

The problem in the no-toll case is that people fail to internalize the additional costs they impose on others when they use the congestible bridge. In a no-toll equilibrium, everyone is just as well off in an environment in which both routes exist than in an environment in which only the highway exists.⁸ If only the highway exists, adding the bridge typically adds no social benefit because commuters simply congest the bridge to the point where there is no time gain to traveling the bridge over the highway. Given the negative externalities present on the congested route, a toll on the bridge can effectively optimize its use by reducing the travel time of some of the drivers on this route. At the same time, no toll is needed on the highway because there are no externalities, since congestion is never present by definition.

The optimal toll minimizes drivers’ total travel time costs.⁹ In a framework with homogeneous values of time, this minimization problem is equivalent to minimizing the total travel time of all drivers, since the monetary equivalent of time costs is the same for all drivers. So if Q commuters use the bridge and (N–Q) commuters use the highway, then the total travel time for all drivers (TT) is given by:

$$ TT = Q \times {t_B} + \left( {N - Q} \right){t_H}. $$

(4)

Minimizing total travel time then gives the optimal distribution of travelers:

$$ Q* = \left( {{t_H} - \alpha } \right)/2\beta . $$

(5)

Another way of determining Q* is by finding the point where MPB equals the marginal external cost (MEC) on the bridge. MEC is positive because an additional driver on the bridge imposes an additional β minutes to each driver already on the bridge. MEC is then:

$$ ME{C_Q} = \sum\limits_{j = 1}^{Q - 1} {\left( {\beta \times {V_j}} \right)} . $$

(6)

In this case, since both β and V _j are constants in this framework, MEC is an increasing linear function, as seen in Fig. 2.

The optimal toll is then defined as the toll that makes travelers indifferent between traveling on the bridge and the highway when Q* drivers travel on the bridge. To find this toll, I must find the monetary equivalent of the difference between highway travel time and optimal bridge travel time. This perceived cost (C) is a linear relation of time, and so I only need to multiply this time difference by the per-minute value of time:

$$ C = \left[ {{t_H} - \left( {\alpha + \beta Q*} \right)} \right] \times V. $$

(7)

Finally, similar to the previous subsection, there exist $\left( {\begin{array}{*{20}{c}} N \\ {{Q^*}} \\ \end{array} } \right)$ possible combinations that lead to equilibrium when the optimal toll is imposed.

2.3 Travel time uncertainty and mixed-strategy Nash equilibria

There is one important item to note regarding equilibria. In previous subsections, each person knows the number of other travelers who take the bridge with certainty. In reality, decisions of others are not known until after each repetition is over. This may lead to subjects favoring mixed strategies over pure ones. Mixed strategies, including those that are Nash equilibria, are analyzed more in the analysis of the experiment, in Section 4.3.1.

3 Experimental design

The two-route travel network from the Pigou-Knight-Downs paradox is used in this experiment both with and without tolls. In each experimental session, 18 subjects must travel from point A to point B using either a congested bridge or an uncongested highway in each round (see Fig. 1).¹⁰ Subjects know that the highway guarantees a travel time of t _H  = 20 min. In contrast, subjects also know that while the bridge is uncongested for the first traveler, and hence has a travel time of 10 min, each additional driver on the bridge adds 1 min to every bridge user’s travel time. In other words, if there are Q subjects traveling the bridge in any round, the travel time for each person is ${t_B} = \left( {9 + Q} \right){\text{minutes}}$, or α = 9 and β = 1 using the notation from the previous section. Each subject may stay on the same route or change from round to round, but no one is permitted to change their choice within a round once their decision has been made. At the end of each round, subjects receive information as to how many people travel on the bridge for that round.¹¹

Each of the 10 experimental sessions consists of three segments with 20 rounds (or repetitions) each, and each subject begins with 8,500 points and a guaranteed $5 show-up fee. Points are deducted for travel time in the first two segments, but not for the third segment. This paper examines the first two segments of the experiment.¹² After the experiment is finished, the remaining points are converted at a rate of 50 points per $1. Each session averages earnings of about $12 to $15 per subject for the experiment, which lasts about 1 h.

3.1 Segment 1: the no-toll case with homogeneous time costs

Subjects are told that each minute of travel time leads to a 10-point deduction, but no tolls are charged. If subjects are profit maximizers, they attempt to choose the route that minimizes their point deduction in every round. This, of course, means that their route choice depends on their expectations about what the other 17 subjects will do in any particular round. Within this framework, theory predicts a user equilibrium with 20 min of travel time on both routes. This occurs when Q = 11.

3.2 Segment 2: the toll case with homogeneous time costs

Subjects continue to pay a 10-point deduction per minute of travel time, but now there is a 60-point per round toll charge. At a cost of 10 points per minute, a 60-point toll translates to the equivalent of 6 min of travel time cost. This means that a 14-minute commute on the bridge is now equivalent (in total point deductions per round) to a 20-minute commute on the highway. So the new toll equilibrium results in a drastic decline in the number of subjects on the bridge, with five people using the bridge, compared to 11 in Segment 1.¹³ This equilibrium also minimizes the total travel time of all subjects. Since travel costs are homogeneous the Segment 2 equilibrium is also efficient, or system optimal.

4 Experimental results

4.1 Data summary and comparison to pure-strategy equilibria

Table 3 reports the average number of bridge travelers per round for each of the experimental groups, with column 2 reporting the average number of bridge travelers in the no-toll case (Segment 1) and column 3 reporting the results for the toll case (Segment 2). Consistent with the theory presented in Section 2, tolls persuade some subjects to change their route choice from the congested bridge to the uncongested highway. Specifically, about five fewer subjects travel the bridge on average in Segment 2 than in Segment 1. This means that an optimal toll is a successful tool to re-route traffic into a more efficient equilibrium.

Table 3 Average number of bridge travelers per round in Segments 1 and 2, by session

For Segment 1, recall that the theory in Section 2 predicts 11 subjects on the bridge and seven on the highway in pure-strategy equilibrium. All of the session averages are within 1.1 of this prediction, with none of these averages statistically differing from 11. Round-by-round results can be seen Fig. 3, while Fig. 4 shows the nearly normal distribution of the number of travelers on the bridge. As seen in Fig. 3, the number of people traveling the bridge often changes after a round is in equilibrium. Although no single subject can be made better off by being the only person to switch routes after equilibrium is reached, some people tend to switch after a round in equilibrium. Session 3 is a good example. Despite the fact that this group has reached equilibrium in Round 3, in the fourth round, two subjects switch from the bridge to the highway, while six switch from the highway to the bridge, resulting in 15 subjects on the bridge. With nearly half of the subjects switching routes after equilibrium is reached, predictions made by a user equilibrium typically do not apply in such a situation. Subjects may also lack full rationality, although testing this is difficult since subjects may be doing what they think is optimal given the actions of others.¹⁴

Fig. 3

Round-by-round results of number of travelers on the bridge for each session, Segments 1 and 2

Fig. 4

Distribution of number of bridge travelers in Segment 1, by round

In Segment 2, theory predicts five subjects on the bridge and 13 on the highway in equilibrium. Unlike Segment 1, some of the group averages significantly differ from this equilibrium. Specifically, Sessions 1, 6, and 8, along with the collective average of all of the groups, significantly average more than five subjects on the bridge per round. This is likely due to a transitioning effect going on from the end of the first segment to the beginning of the second, where subjects may not initially understand the new environment. For example, the first four rounds of Segment 2 for Session 5 result in 13, 8, 7, and 7 bridge travelers, respectively. In the fifth round, the number of bridge travelers is finally below equilibrium for the first time, and equilibrium is finally reached for the first time in the sixth round. As in Segment 1, many of the rounds are out of equilibrium after equilibrium is reached for the first time.

4.2 Efficiency

Given the imposed constant value of time, minimizing total travel time is equivalent to an efficient outcome. As such, social welfare in the route network used in this experiment can be measured by comparing the average travel times between the no-toll and toll schemes. Recall from Section 2.2 that tolls are simply transfers and assumed not to be a cost.¹⁵ So the lower the average travel time is, the higher the social welfare is for a group with homogeneous travel costs. Thus, the lower the overall travel time, the more efficient the outcome of the experiment. Given the imposed homogeneity, comparing average travel times tells something about relative efficiency. Based on the model described in Section 2.2, for a given group of drivers, five or six drivers on the bridge will yield the fewest total number of minutes traveled. This results in the minimum possible total travel time of 330 min.¹⁶ With the 10 sessions of the experiment, the best attainable average time per round is 18.32 min.¹⁷ In Segment 1, the average is 20.20 min, or 10.2% higher than the efficient outcome. In fact, only 2% of the rounds achieved the minimum total travel time possible, which occurs when five or six subjects travel the bridge. In Segment 2, the average travel time is 18.51 min, or 1.0% more than the efficient outcome. Here, 48.5% of the rounds resulted in efficient outcomes.

4.3 Analysis

4.3.1 Comparing mixed-strategy equilibria with the experimental results

In most of Section 2, the discussion focuses on situations in which subjects know with certainty the actions of the other players before making her or his decision. In reality, this does not occur, implying that some or all subjects may decide route choice based on mixed strategies. More evidence supporting the possibility of subjects playing mixed strategies comes from Fig. 3. In this figure, once a pure-strategy Nash equilibrium is reached at any point in the first two segments, one or more subsequent rounds in the same segment are typically not in equilibrium.

Appendix derives a symmetric mixed-strategy Nash equilibrium in Segment 1, with each person playing bridge with probability 10/17. Also from Appendix, the probability of playing bridge in mixed-strategy equilibrium is 4/17 for Segment 2. Note that in mixed-strategy equilibrium for Segment 1, the expected number of bridge travelers is 18 × (10/17), or 10.59, which is less than in the pure-strategy Nash equilibrium prediction. In Segment 2, the expectation is 18 × (4/17), or 4.24 travelers on the bridge, also less than the pure-strategy Nash equilibrium. In Appendix, I show that the total number of travelers on the bridge in Segment 1 is not significantly different from the mixed-strategy prediction at the 5% level.¹⁸ However, in Segment 2, the total number of travelers on the bridge is significantly different from the mixed-strategy prediction. Another measure that can be compared between experimental results and the mixed-strategy prediction is the number of road changes within a segment. As Appendix shows, there are far fewer route changes in Segments 1 and 2 than the mixed strategy predicts.¹⁹ So although there may be some players acting close to the mixed-strategy equilibrium, there appears to be some route “stickiness,” in which once a player is on a particular route, there is an increased tendency to stay on the route in the next round.

4.3.2 Variation in number of bridge travelers by group

Theory predicts the same equilibrium for each group in Segments 1 and 2, specifically 11 and 5 subjects on the bridge, respectively. Note that equilibrium is predicted to be the same in each session. Group-to-group heterogeneity in Segments 1 and 2 can be tested using an F-test. More specifically, the null hypothesis is that the mean number of bridge travelers is the same across sessions. In Segment 1, the average number of bridge travelers per round by group ranges from 9.90–11.35. (See data summary in Table 3 for a more thorough summary.) By finding an F-statistic (in an ANOVA framework) for the difference in means, these averages are not statistically different from each other, with a p-value of 0.743. This is consistent with the theoretical prediction of the same equilibrium in each group. Segment 2’s averages by group range from 5.15–6.00. Again, the averages are not significantly different from each other, with a p-value of 0.978. This is also consistent with the theoretical prediction of the same equilibrium in each group.

5 Conclusions

While theory certainly supports the use of tolls as a mechanism for reducing congestion, there is only limited empirical and experimental evidence examining the functioning of such plans. Consistent with standard theory that assumes homogeneity in time costs across all commuters, on average, the Segment 1 results show that inefficient levels of congestion occur when no tolls are imposed. When tolls are imposed in the same homogeneous time cost framework in Segment 2, the results match the theoretical prediction that fewer subjects choose the congested route.

Although the results reported in this paper, and previous experimental congestion papers, answer some important questions about congestion behavior, further research is necessary to address some nagging problems in congestion experiments. More specifically, the existing experimental results do not match very well with some aspects of congestion theory. In particular, in many experiments, a round in disequilibrium follows a round in equilibrium. The most obvious generalization is to allow for the fact that in reality different people have different values of time, which may affect who decides to travel toll and non-toll routes. The question is, does this type of heterogeneity lead to a stable, or at least more stable, equilibrium?

Appendix

Let p _i equal the probability of person i traveling the bridge and let p_ equal the probability that any one of the other people travels the bridge. If each subject is risk neutral, then maximizing expected utility is equivalent to maximizing expected payout, and also equivalent to minimizing total expected travel time in Segment 1. Let n _B denote the number of travelers on the bridge in any round.²⁰

In Segment 1, if person i travels the highway, the travel time is guaranteed at 20 min, while the expected number of travelers on the bridge is

$$ {\text{E}}\left( {{n_B}\left| {{\text{person}}\,i\,{\text{travels}}\,{\text{the}}\,{\text{bridge}}} \right.} \right) = 1 + 17p\_. $$

(A1)

To find out when person i is indifferent between routes, p_ must be found such that expected travel times are equal:

$$ 9 + \left( {1 + 17p\_} \right) = 20, $$

(A2)

which yields

$$ p\_= \frac{{10}}{{17}} = 0.588. $$

(A3)

Thus, when the expected travel times are equal, person i is indifferent over any strategy. In such a case, each person playing with probability 10/17 (which will henceforth be denoted p) gives a symmetric mixed-strategy Nash equilibrium.

In the mixed-strategy equilibrium described above, the expected number of travelers on each route is 18 * (10/17) = 10.588. This results in fewer expected travelers on the bridge than in the pure-strategy equilibrium. The variance of this distribution is

$$ {V_p} = p\left( {1 - p} \right) = 0.242, $$

(A4)

which results in a standard deviation of 2.088 total travelers in each period.

If Q _H and Q _B denote the total number of expected travelers over 20 rounds on the highway and bridge, respectively, then

$$ {Q_B} = 20 \times 18p = 211.765\,{\text{and}}\,{Q_H} = 20 \times 18\left( {1 - p} \right) = 148.235. $$

(A5)

The variance of the totals in Eq. (A5) is

$$ V = 87.197, $$

(A6)

which results in the variance of the mean of nine groups²¹ of

$$ \frac{V}{9} = 9.689. $$

(A7)

The standard error is then

$$ \sigma = 3.113. $$

(A8)

In the experiment, a per-group average of 217.778 bridge trips are taken in the nine groups with 18 subjects, while the expected number of trips in the mixed-strategy equilibrium is 211.765. Since this difference is about 1.93σ from the mean, a null hypothesis of subjects playing the mixed-strategy equilibrium cannot be rejected at the 5% level.

Similarly, in Segment 2, p _i  = p_ = 4/17, V _p  = 0.180, Q _B  = 84.706, Q _H  = 275.294, V = 64.775, (V/9) = 7.197, and σ = 2.683. In the experiment, a per-group average of 113 bridge trips are taken in the nine groups with 18 subjects, while the expected number of trips in the mixed-strategy equilibrium is 84.706. This difference is more than 10σ from the mean, and so a null hypothesis of subjects playing the mixed-strategy equilibrium can be rejected at a very high level of significance.²²

Another aspect worth examining is whether or not the predictions of mixed-strategy equilibrium are consistent with the number of route changes in the experiment. For each subject playing the mixed-strategy equilibrium in Segment 1, the probability q that a subject will switch routes from one round to the next is

$$ q = 2p\left( {1 - p} \right) = 0.484. $$

(A9)

In Segment 1, there are 19 opportunities to switch routes, leading to 342 opportunities to switch routes for all players within the same group of Segment 1. The expected number of route changes (R) is thus

$$ R = 342q = 165.7. $$

(A10)

Since the binomial distribution is used, the variance is

$$ {V_q} = q\left( {1 - q} \right) = 0.2498, $$

(A11)

which implies that the variance of R is

$$ {V_R} = 342{V_q} = 85.42. $$

(A12)

Since there are nine groups of participants with 18 subjects, it is useful to calculate the variance for the mean of nine observations:

$$ \frac{{{V_R}}}{9} = 9.491. $$

(A13)

The standard error of this variance is thus

$$ {\sigma_R} = 3.081. $$

(A14)

The observed number of route changes per group is 113.78. This is more than 16σ _R below the predicted number of route changes, leading to the conclusion that the number of route changes is inconsistent with the mixed-strategy Nash equilibrium.

In Segment 2, the same calculations lead to q = 0.360, R = 123.1, V _q  = 0.2304, V _R  = 78.78, (V _R /9) = 8.754, and σ _R  = 2.959. The number of route changes per group is 80.56, which is more than 14σ _R below the predicted number of route changes. Again, the number of route changes is not consistent with the mixed-strategy Nash equilibrium.